一种面向直接迭代误差的NLMS-OCF算法研究*

李 茹，翟书颖，李 波

（西北工业大学明德学院，西安710024）

1 引言

归一化最小均方（NLMS）算法由于其低运算量和易于实现而成为最流行的自适应算法之一。而且此算法针对有限字长的效果是健壮的。但高度相关的输入信号在一定程度上降低了它的收敛速度[1-3]。在过去几十年里，有一类等效算法如仿射投影算法（APA）、部分排名算法（PRA）、广义最佳块算法（GOBA）、带有正交校正因子的NLMS算法（NLMSOCF）等已经被用来处理这一问题[4-5]。这些算法的明显特征就是它们更新权重基于多样的、延迟的输入信号向量；而NLMS算法更新权重则是基于一个单一的输入向量。这整个算法类别可被称为仿射投影算法，是因为APA在这些算法中是最早出现的，并且APA这个名字比其它的名字更广泛地使用在现有文献中[6-7]。当延迟D设置为1时，按文献[8]中的解释，APA算法就是NLMS-OCF算法的一个特例。

然而，对于NLMS-OCF算法来说，迭代方向，也称为自适应权重更新方向，是方向向量；而自适应滤波器的迭代误差是由输入向量和自适应滤波器的估计参数引起的。这两个方向是不一致的，从而对于迭代误差导致了更多的偏差。在本研究中，尝试用NLMS-OCF-IE算法解决这一问题。此算法是在无测量噪声的条件下首次提出；迭代误差是直接由方向向量引起，方向向量也是自适应滤波器的迭代方向。相应的仿真实验结果将验证推导的准确性。

2 NLMS-OCF算法

图1显示了一个用在系统辨识模型中的自适应滤波器。如图，系统的输入xn和相应的测量输出dn很可能产生于测量噪声εn污染之后，是已知的。测量噪声εn是零均值复杂白噪声。目标是估计一个N维的权重向量这样当xn=(xn,xn-1,...,xn-N+1)T是在第n个时刻输入的向量时，估计输出在均方误差意义上，尽可能地接近测量输出dn。

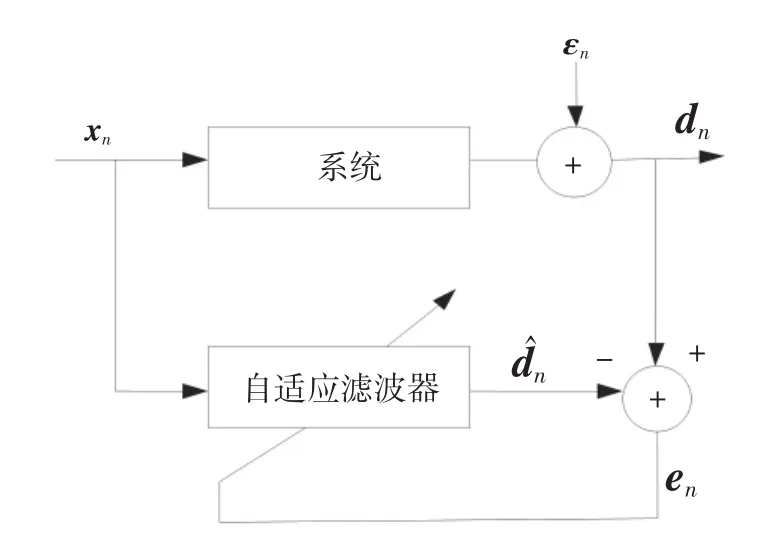
图1 自适应滤波器的辨识模型

在[8]中NLMS-OCF算法总结如下：任意选取一个正交校正因子的数量对于每一个n重复下面的步骤：

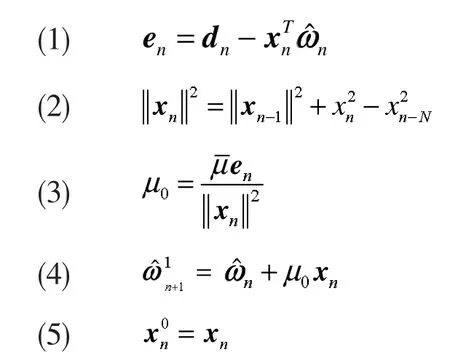
对于 k=1,2,...M，重复步骤(6)～(9)

对于NLMS-OCF算法，从步骤(7)和(9)中可以看出，NLMS-OCF算法权值向量更新的方向是彼此相互正交的，而当D=1时，输入向量xn,xn-D,...,xn-MD几乎是平行的，从而延缓了自适应滤波器的收敛速度。权值向量更新的方向分别是向量xn,但是估计误差分别是由输入向量xn,xn-D,...,xn-MD引起的，除了向量xn，权值向量更新方向和引起估计误差的方向是不一致的，即为了解决这个问题，NLMS-OCF-IE算法需要被提出。

3 NLMS-OCF-IE算法

通过分析在权值向量更新方向上的估计误差，建立了一种NLMS-OCF-IE算法，其估计误差重新定义为：

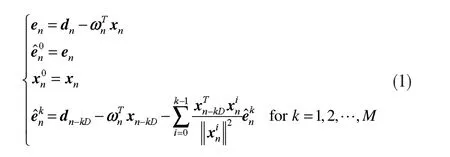
权值向量更新方程式为：

其中

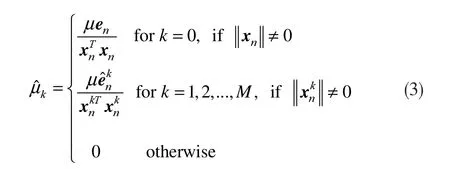
和

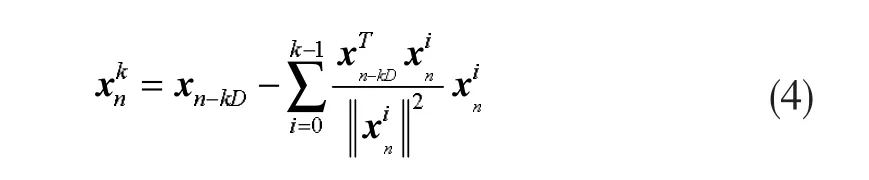
由此，式(1)、(2)、(3)和(4)组成了 NLMS-OCF-IE算法。在下面分析中将证明，在无系统测量噪声的条件下，估计误差仅仅是由向量引起的。

假设存在一个真实的自适应滤波器的N维的权值向量ω0，那么理想的输出应该满足以下表达式

系统测量噪声是均值等于0、方差是的白噪声，其独立于输入向量xn，那么相应的估计误差为

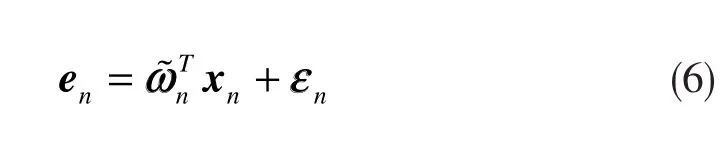
其中

从式(6)中可以知道，在无系统测量噪声的条件下，估计误差en仅仅是由输入向量xn引起的，也就是说它和自适应滤波器的权值向量更新方向是相同的。

从式(1)、(4)、(5)和(6)中，我们可以得到以下的表达形式

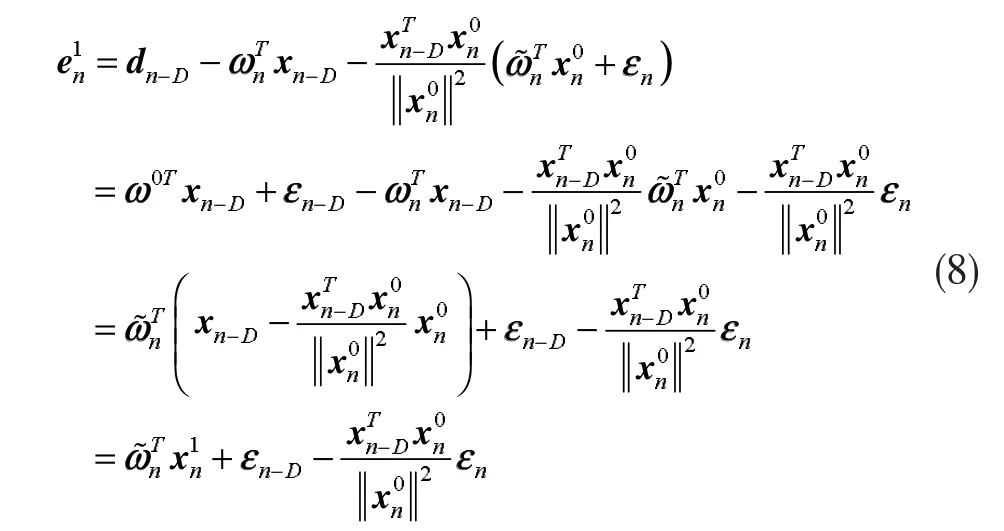
和

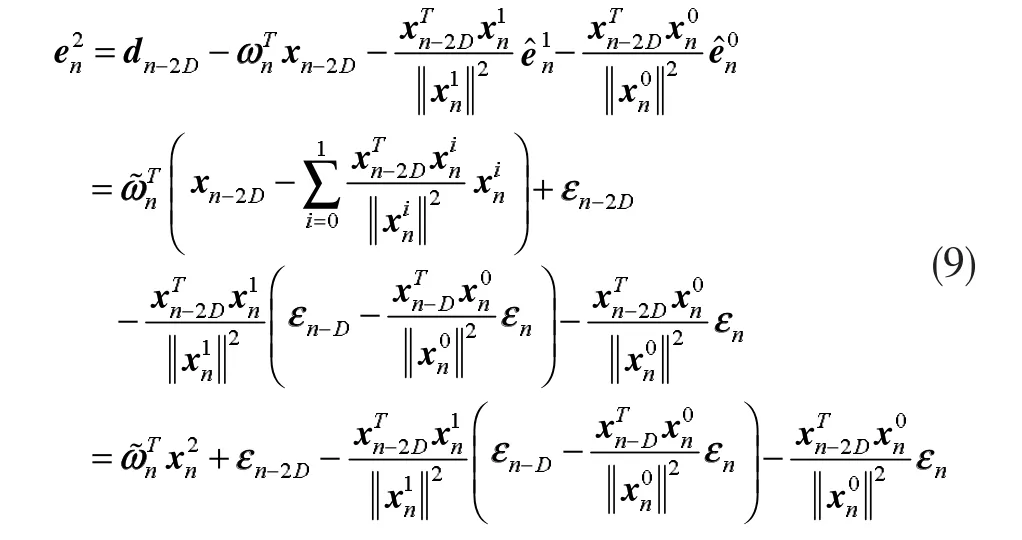
从式(8)和式(9)中可以看出，在无系统测量噪声的条件下，估计误差仅仅是由向量引起的，估计误差仅仅是由向量引起的。下面可以定义：

以此类推，可以得到以下表达式

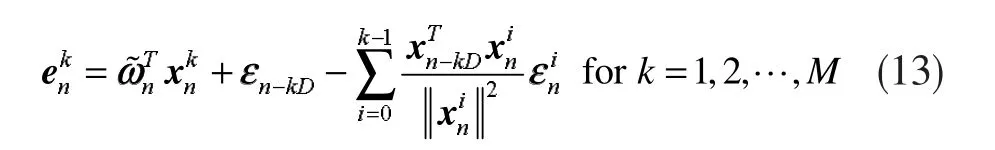
其中

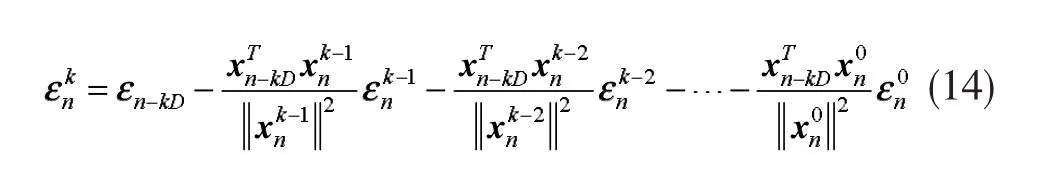
因此，从式(2)、式(3)和式(13)中，可以得出结论:在无测量噪声的条件下，估计误差仅仅是由向量引起的，也就是说当k=0,1,...,M时，它也是NLMSOCF-IE算法的权值向量更新方向。

4 仿真示例

以下分别就NLMS-OCF算法和NLMS-OCF-IE算法在MATLAB中进行了仿真，并对两者的仿真结果做了分析比较。分析包括不同的迭代步长对算法收敛速度产生的影响。仿真结果的MSE学习曲线是通过对100个相互独立的学习曲线求平均值而得到的。参数迭代步长分别选取为0.1和0.5，参数正交校正因子M=3，维数N=32，测量噪声是方差等于0-4的高斯白噪声。当延迟因子D=1时，NLMS-OCF算法与APA算法的特征完全相同，可见APA算法是NLMS-OCF算法的一个特例。因此本文中设置D=1。仿真示例如下。

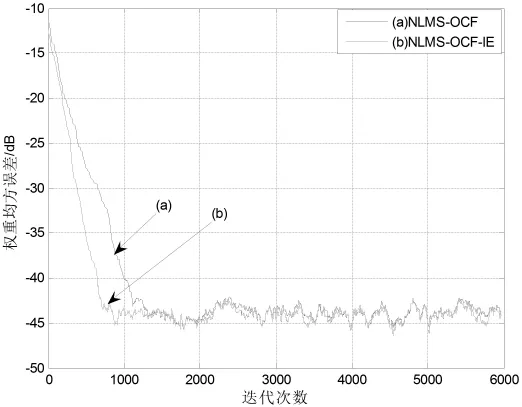
图2 示例1中迭代步长为0.1时的均方误差学习曲线

图3 示例1中迭代步长为0.5时的均方误差学习曲线

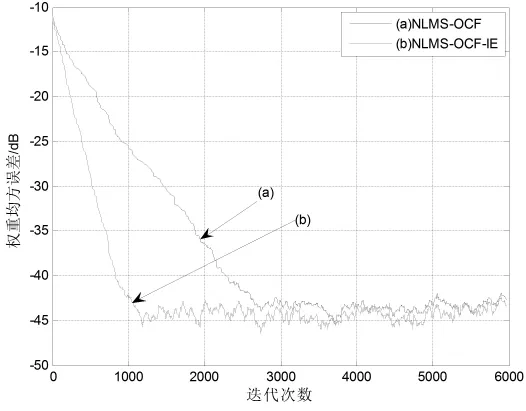
图4 示例2中迭代步长为0.1时的均方误差学习曲线

图5 示例2中迭代步长为0.5时的均方误差学习曲线

示例1：

考虑表达式为xn=-0.5xn-1-0.3xn-2-0.2xn-3+zn的适度相关的输入信号模型，其中zn为均值等于0的高斯白噪声。在此种条件下，对于两种不同的迭代步长值，NLMS-OCF算法和NLMS-OCF-IE算法的权值向量均方误差学习曲线如图2、图3(见前页)所示，从对它们的比较中可以看出，NLMS-OCF-IE算法相比于传统的NLMS-OCF算法得到了比较快的收敛速度，当迭代步长为0.1时效果尤为明显。

示例2：

考虑表达式为xn=-0.95xn-1-0.6xn-2-0.4xn-3+zn的高度相关的输入信号模型，其中zn为均值等于0的高斯白噪声。从图4和图5中可以清楚地看出，相比于传统的NLMS-OCF算法，NLMS-OCF-IE算法表现出了比较快的收敛速度，尤其是迭代步长为0.1时效果比较明显。通过与示例1的比较，可从中发现NLMS-OCF-IE算法对于高度相关输入信号的效果比较显著。

5 结束语

为了修正NLMS-OCF算法迭代方向上的误差，我们提出了NLMS-OCF-IE算法，使得迭代方向和引起估计迭代误差方向相同，从而减小迭代误差，并将改进的算法在MATLAB中进行仿真，仿真结果表明，NLMS-OCF-IE算法相对于传统的NLMSOCF算法，不仅减小了误差，而且还加快了收敛速度，提高了自适应滤波器的性能。

[1]WIDROW B,STEARNS S D.Adaptive signal processing[M].Upper Saddle River,N.J.:Prentice Hall,1985.

[2]HAYKIN S.Adaptive filter theory[M].4th ed.Upper Saddle River,N.J.:Prentice Hall,2002.

[3]SAYED A H.Fundamentals of adaptive filtering[J].Control Systems IEEE,2003,25(4):77-79.

[4]MORGAN D R,KRATZER S.On a class of computationally efficient,rapidlyconverging,generalizedNLMSalgorithms[J].1996,3(8):245-247.

[5]SANKARANSG,BEEXAA.NormalizedLMSalgorithmwith orthogonal correction factors[C]//Asilomar Conference on.IEEE,1997:1670-1673 vol.2.

[6]KIM S E,LEE J W,SONG W J.A Theory on the Convergence Behavior of the Affine Projection Algorithm[J].IEEE Transactions on Signal Processing,2011,59(12):6233-6239.

[7]FAN Y,ZHANG J.Variable step-sizeaffine projection algorithm with exponential smoothing factors[J].Electronics Letters,2009,45(17):911-913.

[8]SANKARAN S G.On ways to improve adaptive filter performance[D].Blacksburg,Virginia,U.S.:Virginia Polytechnic Institute and State University,1999.