基于MATLAB的冲床上下料机械手运动学分析

王守城，王 熙，段俊勇，王小冲

(青岛科技大学机电工程学院，山东 青岛 266061)

冲压加工是一种塑性成型技术，它主要通过压力机加工放入模内的工件，从而获得生产所需尺寸规格的产品。传统冲床的冲压材料由工人手动上下料，效率低下且存在很大的安全隐患，难以实现冲床自动化生产。相对于人工上下料，机械手上下料动作迅速且稳定，可以有效地降低劳动成本、提高工作安全性，促进生产自动化发展[1]；并且机械手重复定位精度高，可以长时间连续作业。

1 机械手结构设计

为了满足冲床加工的上下料要求，机械手采用4自由度的圆柱坐标型传动方案，主要包括腰部的摆动和下降、手臂的伸缩和手腕的回转[2]。机械手运动简图如图1所示，包括X方向、Z方向的直线运动，绕X轴的回转和绕Z轴的摆动。

根据运动简图设计出机械手的总体结构，如图2所示，它主要由基座箱、腰部、手臂、腕部和吸盘端拾器(简称端拾器)5部分组成。该机械手采用伺服电机驱动、丝杠传动，因夹持对象为扁平板材，故采用由气动真空发生器组成的吸盘端拾器。

机械手主要技术参数见表1。

图1 上下料机械手运动简图

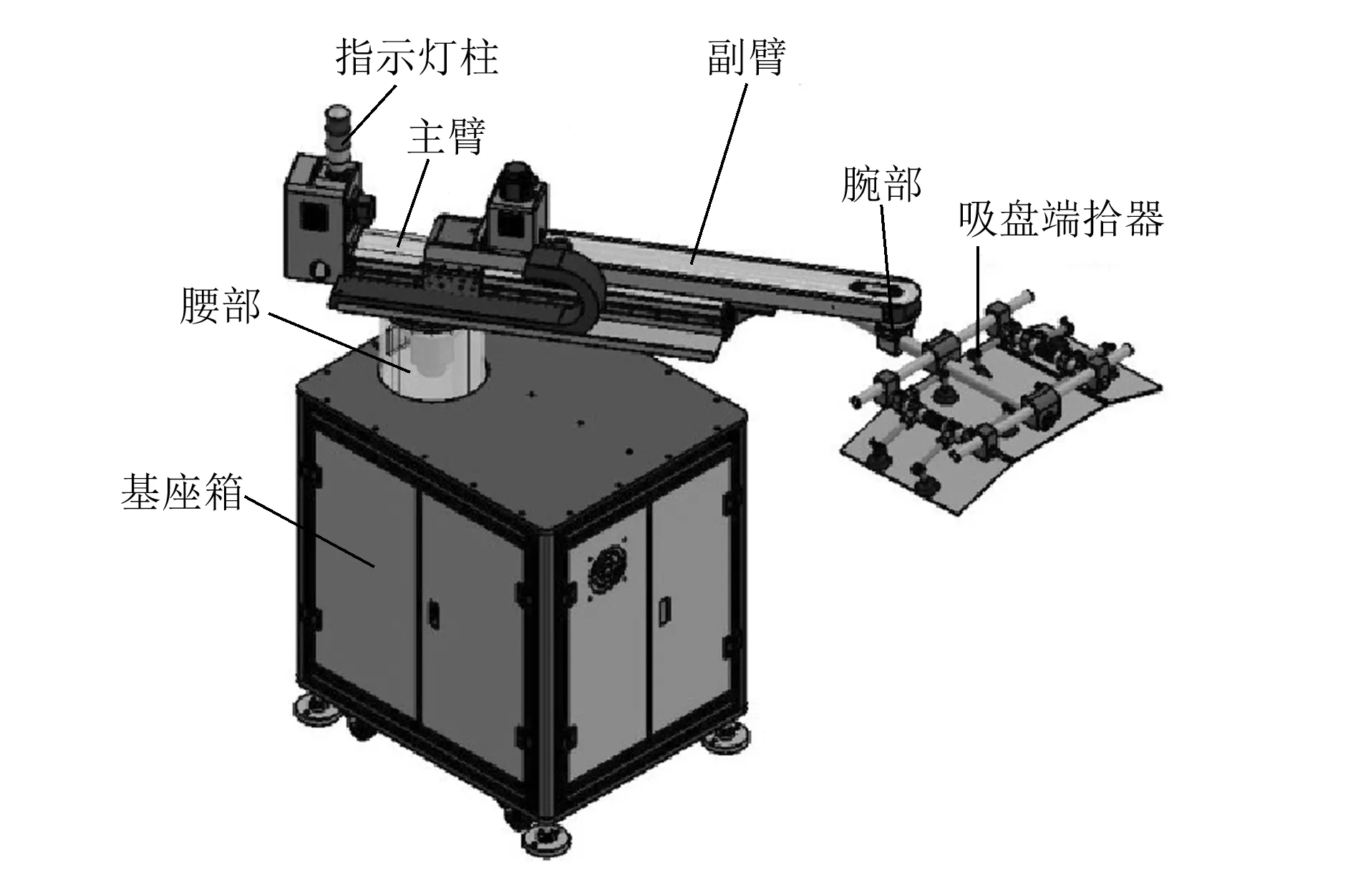
图2 冲床上下料机械手总体结构图

2 运动学分析

2.1 坐标系建立

图3为D-H法连杆坐标系示意图，在机器人学 D-H表示法中，要详细描述各连杆之间的相对变换关系，主要取决于4个关键的几何参数[3]:ai为沿Xi轴，从Zi移动到Zi+1的距离；αi为绕Xi轴，从Zi旋转到Zi+1的角度；di为沿Zi轴，从Xi-1移动到Xi的距离；θi为绕Zi轴，从Xi-1旋转到Xi的角度。

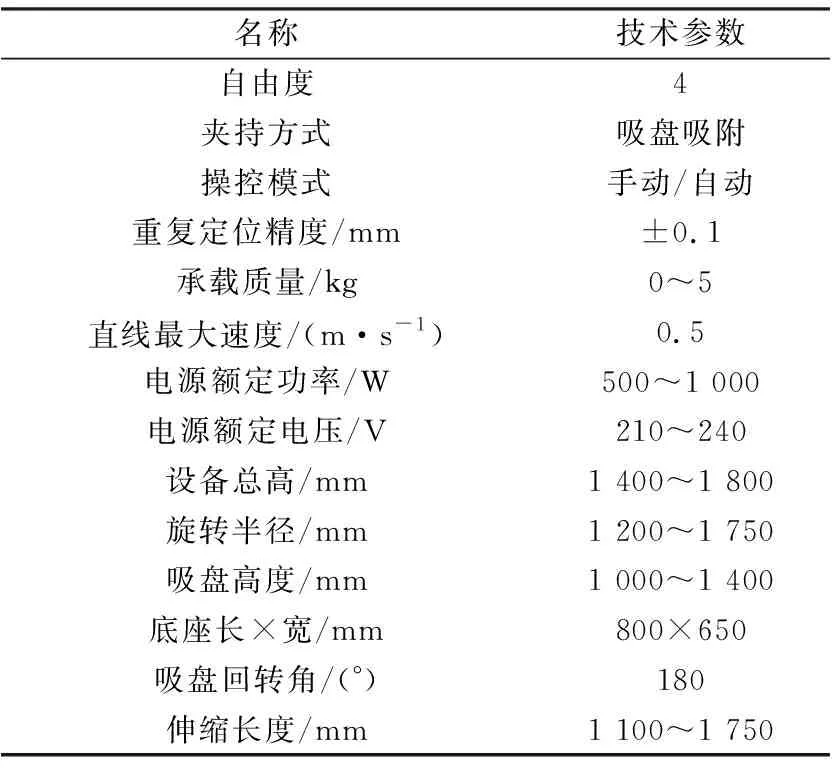
表1 机械手主要技术参数

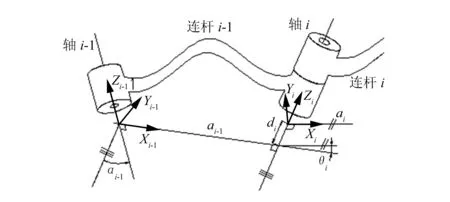
图3 D-H法连杆坐标系示意图

连杆变换矩阵通式为：

(1)

式中：cθi=cosθi，sθi=sinθi，cαi-1=cosαi-1，sαi-1=sinαi-1。

冲床机械手属于4自由度圆柱坐标型机械手，机械手由5部分组成，其中含有4个关节，即腰部1相对于基座0上下伸缩关节、主臂2相对于腰部1的回转关节、副臂3相对于主臂2的前后伸缩关节以及腕部4相对于副臂3的旋转关节。端拾器5无主动运动，依靠真空吸盘吸附在工件表面来抓取工件，在运动学分析时无需考虑其运动状态。分别对这几部分建立连杆坐标系，而连杆坐标系的设定不唯一，关节1,2,4,5的轴线为垂直方向，关节3的轴线为水平方向，用CAD构建的连杆坐标系如图4所示。根据机械手的结构设计，可知a1=170mm，d2=750mm，d4=90mm，d5=100mm，a4=350mm。

综合管理信息平台的建立能够为基层管理人员提供实时准确的数据信息，为中层管理人员提供详细的管理信息，为高层管理者提供决策信息，提高整个学校的办公效率和管理水平，最终实现“数字化校园”的构想。

图4 冲床机械手连杆坐标系示意图

根据D-H表示法，机械手连杆参数和关节变量见表2。

表2 冲床机械手连杆D-H参数

2.2 机械手正运动学求解

将连杆变换矩阵相乘得机械手总体变换矩阵为：

(2)

2.3 机械手逆运动学求解

机械手逆运动学求解是在已知机械手末端部分位姿的情况下，去求解机械手各关节的变量，从而确定各关节所需电机的输出力矩的大小和方向，这样机械手各关节和末端部分在空间设定点的位姿状况就可以确定[4]。

这里采用代数解法求解，如果机械手的末端部分的位姿已经确定，即假定的末端部分位姿矩阵为:

(3)

式中：n为法向向量；o为滑动向量；a为机械手接近向量；p为机械手位置向量。为了求解相应的角度和距离，依次用逆变换左乘式(3)的两边。本文直接利用矩阵方程两端的元素对应相等得到方程组，从而求得关节变量。

得方程组：

解方程组得：

从机械手运动学逆解的求解情况可以看出，逆解分为存在或不存在两种情况。另外，非零的连杆参数越多，机械手要到达某一位姿，其运动学逆解就会越多。因此，机械手各个关节移动量，应该在保证互补干涉和节省资源的前提下，择优选择行程原则。

3 机械手MATLAB仿真

3.1 建立仿真模型

采用Robotics Toolbox里的Link函数来构建机械手关节模型[5]。构建模型前需要确定各关节变量及其他D-H参数，d1的变化范围为0～500mm，d3的变化范围为0～650mm，θ2的变化范围为-90°～90°，θ4的变化范围为-180°～180°。构建模型如图5所示。

图5 机械手仿真模型

可以利用drivebot函数驱动机械手，使机械手能够在空间运动。图6所示为机械手驱动控制面板，建立4个调节滚动条，滚动条调节范围即是关节变量的活动范围，这样就实现了整个机械手在空间的运动。

图6 机械手滑块控制面板

3.2 机械手MATLAB正逆运动学求解

采用fkine函数验证正运动学的正确性。定义机械手末端起点A的4个关节变量为qz=[0.10 0 0.15 0]，运用fkine(r,qz)函数，将返回机械手末端执行器相对参考坐标系变换的位姿矩阵在MATLAB里运行后得：

将A点的关节变量代入式(2)并计算，其结果与MATLAB中计算结果一致，证明本机械手运动学方程正确。

MATLAB中对机器人逆运动学求解可以利用Robotics Toolbox中的ikine函数。设冲床机械手终点B在关节坐标系的齐次变换矩阵为：

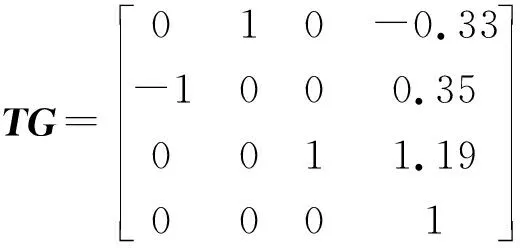
TG代表运动学的逆解，MATLAB程序运行得到B点关节变量：qr=[0.45 1.57 0.50 -3.14]。同理也可以将TR代入程序，这样正逆运动学在MATLAB中同时得到验证，而B点的关节变量值也可代入式(2)，所得结果与上述一致，则运动学方程正确。

3.3 机械手轨迹规划仿真

本机械手的轨迹规划仿真采用点到点关节空间内规划，规定起始点为qz=[0.10 0 0.15 0]，终止点为qr=[0.45pi/2 0.50pi]，且机械手在起始点与终止点的初速度和末速度都为0，所需运动时间t=2s。

采用Robotics Toolbox模块中jtraj函数来进行关节空间规划[6]，主要完成端拾器的空间规划，其轨迹如图7所示。

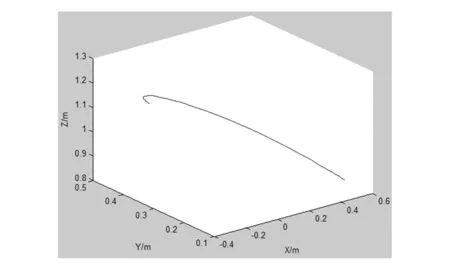
图7 机械手端拾器空间轨迹图

对机械手建立仿真模型并进行轨迹规划后，利用fkine函数计算机械手向前运动的齐次变换矩阵，得出4个关节的(角)位移、速度和加速度变化曲线，如图8所示。

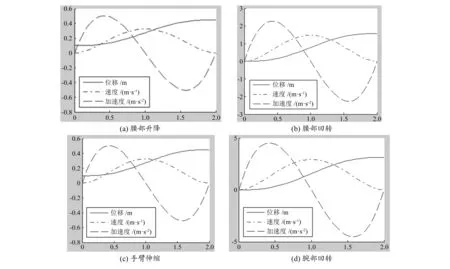
图8 各轴运动学参数随时间变化曲线

从图8中可以看出4个关节的运动学参数都是随时间而平缓变化，速度(角速度)曲线、加速度(角加速度)曲线都是正弦或余弦曲线，不含突变，说明运动过程不含刚性及柔性冲击，机械手运行稳定。

4 结束语

为应对人工上料效率低以及存在安全隐患等问题，本文设计了一种冲床自动上下料机械手，通过正逆运动学分析以及MATLAB的建模仿真，证明设计的机械手可以满足工作要求，并且运行过程平稳无冲击。后期还需要结合实际生产对机械手杆臂进行一系列的参数优化，保证机械手更加完善。本机械的应用可以缩短生产周期、降低劳动成本，促进冲床生产自动化的发展。

参考文献：

[1] 王月芹.基于 PLC 的机械手控制系统设计[J].液压与气动,2011(9)：41-43.

[2] 马香峰.机器人机构学[M].北京：机械工业出版社,1991.

[3] 陈则仕，张秋菊.D-H法在五轴机床运动学建模中的应用[J].机床与液压，2007,35(10)：88-90.

[4] 王战中，张俊，季红艳，等.自动上下料机械手运动学分析及仿真[J].机械设计与制造，2012(5)：244-246.

[5] 陈燕,邹湘军,徐东风,等.荔枝采摘机械手机构设计及运动学仿真[J].机械设计，2010,27(5)：31-34.

[6] WANG Ke, ZHOU Jiping. Kinematical analysis and simulation of high-speed plate carrying manipulator based on MATLAB[J].Engineering，2012,4(12):850-856.