结合点云数据与BIM技术的古建筑三维重建与信息化管理

王令文(上海岩土工程勘察设计研究院有限公司,上海 200438)

点云数据是三维信息最直接的表达方式，虽能反映目标物的基本形态，但其散乱无序、无空间拓扑关系，且可视性较差，因此需对其进行三维重建。目前，物体的三维模型可以用三角网格模型、多边形模型、NURBS曲面模型、实体模型等近似模拟。其中，三角网格模型最为常见，比较经典的有微切平面法[1]、Delaunay剖分法[2-3]、隐式曲面法(径向基函数法RBF[4]、移动最小二乘法MLS[5]、多层次统一分区法MPU[6]等)、区域生长法(Ball-pivoting算法[7]、DBRB:delaunay-based region-growing algorithm[8]等)等。Delaunay剖分法应用最广，主要有降维剖分法[9]和四面体剖分法[10]。其中，前者原理简单，运行效率较高，但抗噪性较差，不适合建筑、文物、雕塑等具有复杂曲率特征的物体表面重建；后者适用性更好，能够准确、精细地再现物体表面，但计算过程数据量大，适合规模较小的复杂物体重建。实体模型较三角网模型精细度略差，通过构建规则的实体，并经过布尔运算得到整个物体模型，模型的数据量小，适合规则物体的重建。因此，本文提出一种综合建模策略，结合三角网模型和实体模型的优势，基于点云对古建筑中的复杂部位构建其三角网模型，而对于较为简单、规则的部位则直接构建其实体模型，并在BIM(building information modeling)的实施平台Autodesk Revit中以点云为参考，实现所有模型对象的精确组合。此外，考虑到古建筑包含的文化内涵异常丰富，但由几何模型直接传递出来的信息十分有限，本文借助建筑信息模型的特点，在Autodesk Revit中实现古建筑各构件的几何模型和属性信息的共同管理。

1 古建筑三维建模

1.1 基于Delaunay四面体剖分的三维重建

Delaunay四面体剖分法的主要实现步骤如下：

(1) 散乱点云网格初始化。首先，在三维空间散乱点集S中搜索点云数据的最大坐标值和最小值坐标：Xmax、Ymax、Zmax、Xmin、Ymin、Zmin，并以此构建该点集的长方体包围盒[11]。然后，根据包围盒的边界确定一个辅助六面体，使其能够包围所有的点云数据。最后，将该辅助六面体拆分为5个四面体，完成网格的初始化。

(2) 在四面体网格中添加新节点Pi(Xi,Yi,Zi)，并构造该节点的Delaunay腔。

(3) 连接Pi(Xi,Yi,Zi)与Delaunay腔中所有节点，将Delaunay腔剖分成新的四面体网格，并将新的节点和四面体网格加入到各自的队列中。

(4) 更新数据结构,若新节点队列非空,则返回步骤(2)，否则，结束剖分。

1.2 基于Revit的实体模型构建

Autodesk Revit系列软件是Autodesk公司推出的一款三维参数化设计软件。软件中用于组成信息模型的构建都是利用“族”工具创建的，通过“族”构件的组合生成整个模型[12]。因此，“族”构件的生成是基于Revit建模的关键。Revit中的“族”可以分为：可载入族、系统族和内建族。其中，可载入族是使用族样板在项目外创建的RFA文件，可以载入到不同的项目中；而系统族和内建族均是在项目内创建和修改，系统族可以在项目和样板间复制和粘贴，内建族只能在当前的项目文件里使用。综上考虑，本文以点云为参照，采用“可载入族类型”生成物体的“族”构件。实体模型构建的主要步骤如下：

(1) 构件分类与点云分割。根据构件类型对古建筑整体进行分类[13]，并依据分类情况，对点云数据进行分割，作为构建单个“族”模型的数据参考。

(2) “族”几何模型的构建。创建“族”模型时常选用“公制常规模型.RFT”“基于面的公制常规模型.RFT”和“基于线的公制常规模型.RFT”样板。在族编辑器中打开要使用的样板，通过导入点云、CAD图形、图片作为参考，利用拉伸、融合、旋转、放样、放样融合等命令绘制每个构件的“族”的几何模型。

1.3 模型建立

考虑Autodesk Revit以“族”为对象，首先将基于Delaunay四面体剖分算法生成的网格模型导入Revit中，直接转换成“族”模型；其次，在Revit中创建新项目，导入点云文件作为参考，创建相应的参考面和参考线；最后，将前期制作的所有“族”模型导入项目中，并基于参考线或参考面进行精确组合，获得最终的三维模型。

2 三维模型的信息化管理

三维模型的管理大致经历了实体档案管理、数字化管理和信息化管理3个阶段[14]，三维模型的信息化阶段，用户不仅可以对三维模型信息进行管理和检索，还可以在虚拟场景中直接进行交互式、可视化、全面动态的信息服务。GIS技术、BIM技术对三维模型的信息化管理有着至关重要的作用。其中，GIS技术主要用于大范围的空间信息管理，而对模型的单体构件描述较少[15]。BIM技术则以实体的单个构件为对象，将构件真实的几何信息、属性信息及构件间的关联信息封装在同一模型框架，提供程序系统充分的计算依据，使系统能够自动计算出查询者所需要的准确信息。正因为BIM中各类信息都源自同一个模型，信息之间具有统一性和联动性，当对某一个信息进行修改时，其他与之有关的信息能够随之进行参数化联动。且BIM软件中可以链接栅格图像、CAD矢量数据、点云数据等，因此可以实现对传统纸质和数字化资料的持久利用。

2.1 古建筑三维模型的信息化管理内容

本文利用BIM的实施平台Autodesk Revit从以下方面对几何和属性信息都有较高要求的古建筑三维模型进行三维化、信息化和协同化管理，如图1所示。

2.2 信息录入与关联

Revit既可为项目设置建筑名称、作者、项目状态、项目地址、项目名称等项目属性信息，用于存档及后期的查询和应用，又能够设置项目的各类尺度单位和舍入(即保留几个小数位)信息，用于后期的计算和分析。

按照本文介绍的方法建立古建筑的几何模型，为模型的每个构件分别录入尺寸、材质、文化背景、艺术风格、年代等属性信息。并通过导入和链接的方式插入Revit、CAD、gbXML、栅格图像、点云等信息，实现对传统资料的持久利用。Revit通常以表格的方式对这类信息进行管理，可以在表格中查看链接文件的状态、大小、路径等信息。

2.3 信息的修改与维护

模型信息的修改主要包括图形样式及参数的修改。图形样式的修改主要指图形形状的更改；参数的修改包括参数的添加、删除、重命名及参数值的修改，其中单个参数值的修改可以直接通过该构件的类型属性对话框进行，多个构件的某一参数值的修改可通过修改明细表进行。

Revit软件中模型信息相互关联，信息的修改具有联动性，无需对各个视图逐一进行修改，极大地提高了模型修改的效率，降低了由于模型修改过程中的疏忽造成的全局不一致性。此外，在对模型进行修改的同时，可以利用Revit软件的阶段化功能，将每次的修改在不同阶段中进行，便于日后的查询和管理。

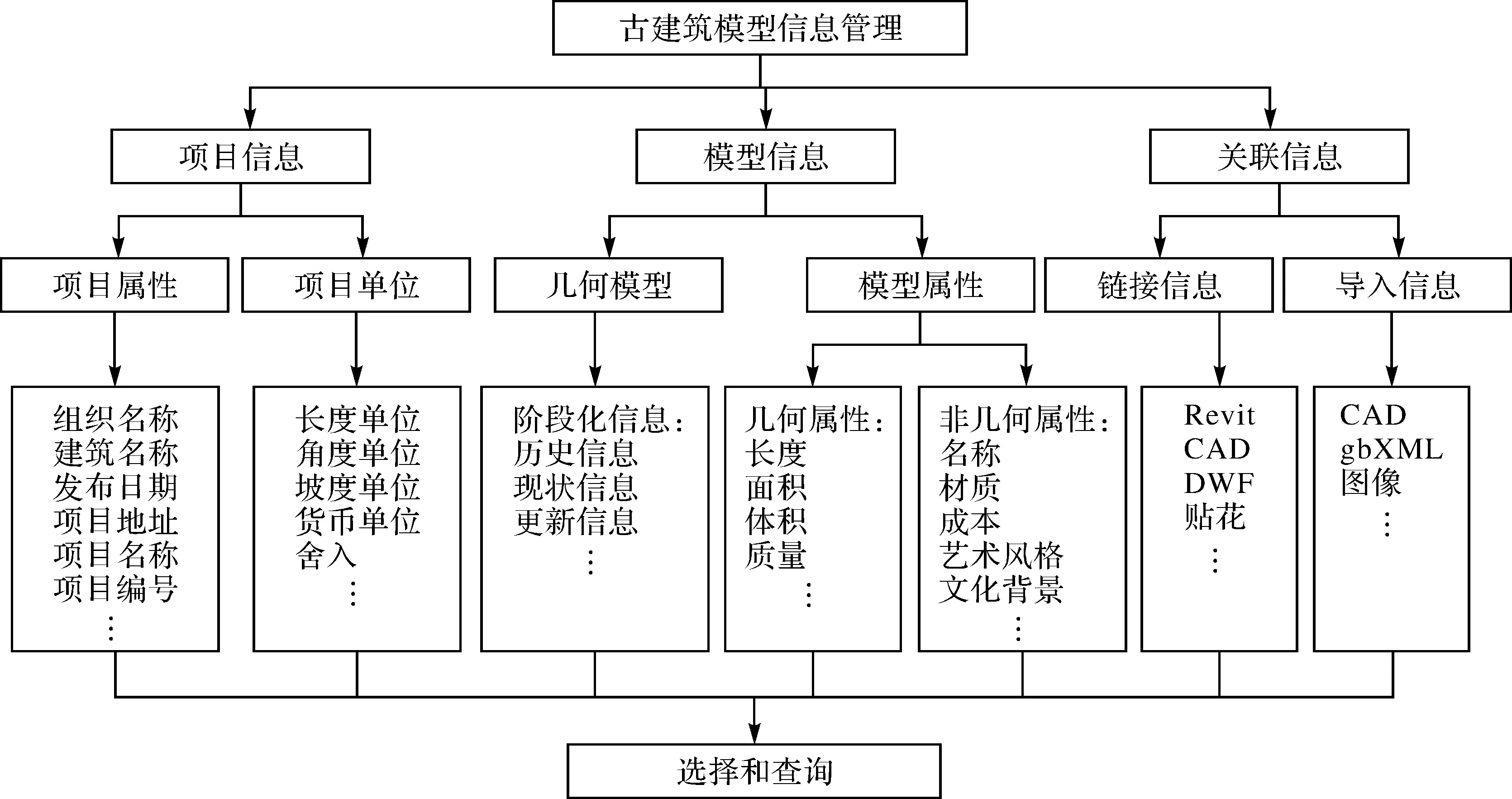
图1 古建筑三维模型的信息化管理内容

2.4 模型的阶段化管理

对建好的模型进行阶段化管理，为每个模型构件添加工程阶段，设置阶段化状态。模型的阶段化管理具有以下优点：

(1) 可利用阶段过滤器选择不同阶段的模型，从而迅速查阅已拆除构件、正在修复构件、已修复构件及新构件。

(2) 可定位已损坏构件，及时进行修复。

(3) 当对古建筑的某个构件进行修复后，可在原模型的基础上添加该构件的新模型，对构件的原模型进行替换。

3 试 验

本文试验以一个既有复杂曲面又有规则构件的六角亭为对象，根据本文的建模方案，针对亭子中的屋顶复杂部位，采用基于Delaunay的四面体剖分法直接生成三角网模型；针对亭子中的柱子、柱础、挂落、飞来椅等规则部位，则采用在Revit中直接生成实体“族”模型的方法；最后，将所有的“族”整合在一起，生成最终模型。

3.1 点云分割及“族”模型构建

根据构件类型对该六角亭的点云数据进行分割，并分别构建其“族”模型，点云分类分割和“族”模型效果见表1。

表1 六角亭分割后点云及其“族”模型

3.2 整体模型构建

在项目中通过链接的方式导入点云基准，依据点云基准创建参照面和参照线，为“族”模型的空间位置提供参考。“族”模型只能在该参考面或参考线上移动，在此基础上通过捕捉点云确定每个“族”模型的精确位置，从而构建出整体模型，三角面片数为431 970个，如图2所示。

图2 六角亭模型与链接点云叠合效果

由图2可见，本文所建模型十分逼真，细节还原度高，且整体效果较好，与用扫描仪直接采集的点云吻合度高。

3.3 建模效果的比较和评价

为突出本文建模方法的优势，将本文建模效果与Geomagic软件点云封装效果进行比较。图3为利用Geomagic软件对亭子点云封装后的效果，三角面片数为1 895 527个。对比图2和图3可见，Geomagic软件生成的亭子模型不仅存在大量细小三角形和孔洞，而且数据量较大，而本文所用的建模方法所建的模型较为完整，可视化效果更好，且数据量较小，三角面片数仅为前者的22.8%。

图3 Geomagic中六角亭点云封装后效果

为量化建模精度，将利用本文方法所建的模型与预处理后的点云叠合，进行偏差分析，偏差结果如表2 和图4所示。

表2 六角亭模型与点云3D偏差分析

注：均值：14.96 mm；标准差：11.77 mm。

图4 六角亭模型与点云3D偏差分级显示图

由表2和图4可见所建模型与实际点云叠合度较好,偏差值可以控制在25 mm以内，较大的偏差出现在点云稀疏处。

4 结 语

本文在分析了三角网模型和实体模型优缺点的基础上，提出了一种综合建模策略。针对古建筑的复杂部位，基于点云构建其Delaunay三角网，而对于较为简单、规则的部位，在三维激光扫描点云的参照下直接构建其实体模型，并分别从项目信息、模型信息、关联信息这3个方面对基于BIM的模型信息化管理进行了探讨。通过六角亭试验证明了本文的建模方法可以以较少的三角面片数量高精度地还原物体的表面模型，可为规模较大、目标实体众多、表面复杂形的大场景古建筑建模提供一定的借鉴。本文所提出的古建筑信息化管理方法可以分阶段对建筑的每个构件进行持续高效管理，并可以自定义过滤器，选择模型中的特定构件，快速查询其属性信息，可用于古建筑修缮过程中的全生命周期管理。

参考文献：

[1] HOPPE H，DEROSE T，DUCHAMP T，et al.Surface Reconstruction from Unorganized Points[J].Computer Graphics，1992，26(2):71-78.

[2] 倪小军.点云数据精简及三角网格面快速重构技术的研究与实现[D].江苏:苏州大学，2010:17-18.

[3] 李巧丽.基于点云数据的塑像三维建模[D].上海:同济大学,2009:63-69.

[4] CARR J C，BEATSON R K，CHERRIE J B，et al.Reconstruction and Representation of 3D Objects with Radial Basis Functions[C]∥Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM，2001:67-76.

[5] LEVIN D.The Approximation Power of Moving Least-squares[J].Mathematics of Computation of the American Mathematical Society，1998，67(224):1517-1531.

[6] OHTAKE Y，BELYAEV A，ALEXA M，et al.Multi-level Partition of Unity Implicits[J].ACM Transactions on Graphics(TOG)，2003，22(3):463-470.

[7] BERNARDINI F，MITTLEMAN J.The Ball Pivoting Algorithm for Surface Reconstruction[J].Visualization and Computer Graphics，l999，5(4):349-359.

[8] KUO C C，YAU H T.A Delaunay-based Region-growing Approach to Surface Reconstruction from Unorganized Points[J].Computer-aided Design，2005，37(8):825-835.

[9] 张书睿，张鹏程.一种三维散乱点局部降维Delaunay网格自动生成算法[J].电子技术与软件工程，2016(10):182-183.

[10] WATSON D F.Computing the N-dimensional Delaunay Tessellation with Application to Voronoi Poly Topes[J].The Computer Journal，1981，14(2):167-172.

[11] 琚俏俏,程效军,徐工.基于椭圆拟合的隧道点云去噪方法[J].工程勘察,2014(9):69-72.

[12] 孙伟超.基于Revit Architecture的古建筑信息模型系统设计初探[D].天津:天津大学，2012:10-11.

[13] 罗翔，吉国华.基于Revit Architecture族模型的古建参数化建模初探[J].中外建筑，2009(8):42-44.

[14] 朱磊.中国古代早期木结构建筑信息模型(BIM)建构的实践分析[D].天津:天津大学,2012:18-19.

[15] 刘昊.基于点云的古建筑信息模型(BIM)建立研究[D].北京:北京建筑大学，2014:1-3.