Exponentiated Weibull大气湍流下混合RF/FSO系统容量分析

张 韵,王 翔,赵尚弘,蒙 文,赵 静

(空军工程大学信息与导航学院,陕西 西安 710077)

1 引 言

自由空间光通信(FSO)以其高速率、抗干扰性强、成本低及带宽容量大等优点引起广泛关注,在无线通信领域的应用广泛[1]。但FSO的局限性在于传输质量受天气状况及大气湍流影响严重[2]。而射频(RF)通信技术具有强大的环境适应能力,对云、雾等天气及障碍物遮盖不敏感,因此,RF/FSO混合通信是一种解决恶劣天气对无线通信系统造成影响的新型方案[3],综合考虑FSO与RF各自优势将两种通信系统互为备份组成混合RF/FSO通信系统[4]。两种链路互为补充,将满足高有效性大容量信息传输。

目前,国内外很多研究团队对混合RF/FSO通信系统性能进行了相关研究。混合RF/FSO有三种方式:(1)在空间分集技术条件下,将RF链路作为数据复制和恢复链路。由于RF与FSO链路数据速率相差较大,故需在FSO链路采用自适应速率算法使得系统可用[5]。(2)RF与FSO链路并行传输,此通信系统可靠性高但存在资源浪费,对发射端要求高的问题[6]。(3)将RF链路作为备用链路,当FSO通信性能差时切换至RF链路进行通信[7]。本文研究第三种混合RF/FSO通信系统,为减少混合RF/FSO通信中链路切换次数,提高系统可靠性,建立复杂通信环境下大容量信息传输系统,应用马尔科夫链设置双门限实现通信链路切换。2012年,Barrios R和Dios F提出了全新的适用于弱到强湍流及孔径平均下的Exponentiated Weibull分布模型[8-9]。因此,面向未来军事航空激光通信复杂的大气条件,本文基于Exponentiated Weibull 分布大气湍流模型,分析了双门限混合RF/FSO通信系统的平均信道容量。

2 双门限RF/FSO模型

2.1 RF/FSO系统模型

混合RF/FSO系统中,FSO链路作为优先使用链路,RF链路作为后备支援链路。当FSO链路不可用时,切换至RF链路进行通信。FSO信噪比与信道配置的关系表达为式(1)[5],当信噪比大于γH时,采用FSO链路通信。当信噪比低于γL时,通信系统切换至RF链路通信。在信噪比为γL和γH之间时,系统采用上一时刻所使用的通信链路。系统模型可定义为具有三个状态的马尔科夫链。

(1)

假设自由空间光通信系统采用开关键控(OOK)强度调制直接检测(IM/DD),信道受大气湍流影响且具有独立同分布且无记忆平稳遍历的加性高斯白噪声,则系统瞬时信噪比表达式如下[10]:

(2)

式中,R为光电转换效率,h=hthp,其中ht为大气湍流衰减因子,hp为指向误差衰减因子,Pt为平均发射功率,n为均值为0,方差为σn2的加性高斯白噪声。系统平均信噪比表达式为[10]:

(3)

2.2 大气湍流信道衰减模型

现有的激光链路的大气湍流模型大多基于Lognormal分布模型和Gamma-gamma分布模型。但是上述两种模型的适用范围不同。Lognormal模型适用于弱湍流条件下,Gamma-Gamma模型适用于中强湍流条件下。2012年,Barrios R和Dios F提出了全新的适用于弱到强湍流及孔径平均下的Exponentiated Weibull分布模型,故本文采用Exponentiated Weibull分布模型[8]。

(4)

其中,α>0,β>0；η为与光强有关的参数,且η>0,通过曲线拟合的方法得到经验公式:

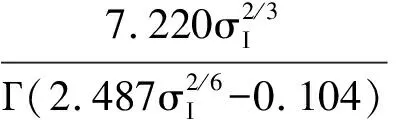
(5)

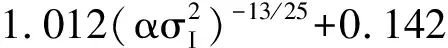
(6)

(7)

2.3 指向误差模型

系统中大气湍流与链路指向误差共同影响接收光信号的强度,由指向误差理论得光链路指向误差因子hp的概率密度函数可表示为[10-11]:

(8)

信道衰减因子h=hthp的联合概率密度函数可计算为[10-11]:

(9)

利用Meijer G函数的性质[12]推导得信道衰减因子h的联合概率密度函数的闭合表达式为:

(10)

3 信道容量

由式(1)可得通信系统采用RF链路通信的概率为:

(11)

将式(10)代入式(11)中得:

(12)

通信系统采用FSO链路的概率为:

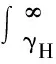
(13)

将式(10)代入式(13)中得:

(14)

综上,当信噪比介于γL和γH之间时的概率表达式为:

pn(1)=1-pn(0)-pn(2)

(15)

假设在信道的接收端和发射端,理想的信道状态信息可用,则FSO链路的平均容量为[5]:

(16)

式中,B为带宽,将log2(·)用MeijerG函数表示得[12]:

(17)

将公式(10)代入公式(16),利用MeijerG函数运算性质[12],得到FSO链路平均容量表达式为:

(18)

式中,Δ(K,A)=A/K,A+1/K,…,A+K-1/K;l和k为满足l/k=β/2的整数。

假设在信道的接收端和发射端,理想的信道状态信息可用,则由式(1)表达的马尔科夫链状态可知,则通信系统的平均信道容量表达式为:

(19)

其中,Ci表示式(1)中状态Si的容量;pi(s)表示状态Si的概率即上文求出的式(12)、(14)及(15)。状态Si采用上一时刻所使用的通信链路,为简化运算,假设状态Si使用FSO、RF链路的可能性相同。则可得系统平均信道容量表达式为:

(20)

4 仿真分析

为研究不同参数对混合RF/FSO系统平均信道容量的影响,根据式(20)进行仿真分析,假设RF链路一直可用且不受天气影响,故RF信道容量为恒定值,取值为FSO链路在L=20 km,σs/r=0.5,wz/r=1,Cn2=1×10-14,SNR=6 dB时信道容量的40%。表1为系统设置参数。

表1 仿真参数

图1为L=20 km,σs/r=0.5,wz/r=1时,不同大气湍流强度下,平均信道容量随信噪比的变化关系。由图可知大气湍流强度增大使信道容量减小,且在强湍流条件下影响较大,提高信噪比能够增加信道容量。如在信噪比为6 dB时,与湍流强度Cn2=3×10-15时相比,湍流强度为Cn2=1×10-14,和Cn2=1.3×10-13时平均信道容量减少了5.7%及24.5%；在湍流强度为Cn2=1×10-14时,与信噪比为2 dB 相比,信噪比为4 dB和6 dB时平均信道容量增加了26.8%与42.1%。

图2仿真了中湍流强度Cn2=1×10-14,σs/r=0.5,wz/r=1时,不同传输距离下,平均信道容量随信噪比的变化关系。由图可知,信道容量随传输距离增加而减小,提高信噪比能够增加信道容量。如在信噪比为6 dB条件下,L=15 km时,平均信道容量C=10.454,L=20 km时,平均信道容量为C=8.532,L=25 km时,平均信道容量为C=7.008。

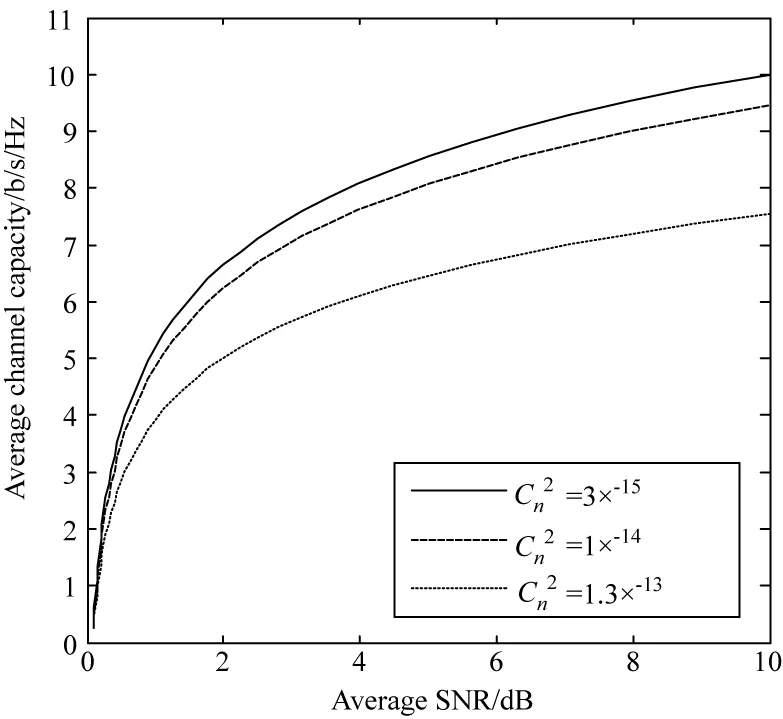
图1 L=20 km,σs/r=0.5,wz/r=1时, 不同大气湍流强度下,平均信道容量随信噪比的变化关系

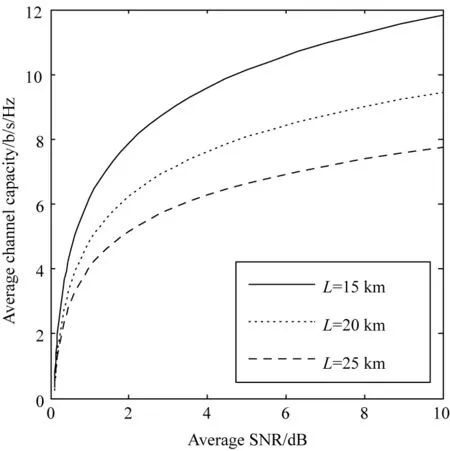
图2 当Cn2=1×10-14,σs/r=0.5,wz/r=1时,不同传输距离时,平均信道容量随信噪比的变化关系

图3为在中湍流强度Cn2=1×10-14,L=20 km,σs/r=0.5条件下,不同接收端处波束宽度与接收机比值wz/r时平均信道容量与信噪比的关系。由图可知,随着wz/r增大即几何传播损耗增大,链路平均信道容量减少。信噪比的增加可以补偿几何传播损耗对链路性能造成的影响,使链路平均信道容量增大。如在wz/r=0.8条件下,与信噪比为2 dB相比,信噪比为4 dB与6 dB平均信道容量增加了22.7%和37.9%。wz/r=1,wz/r=1.2条件下信噪比增大对平均信道容量的影响效果近似相同。

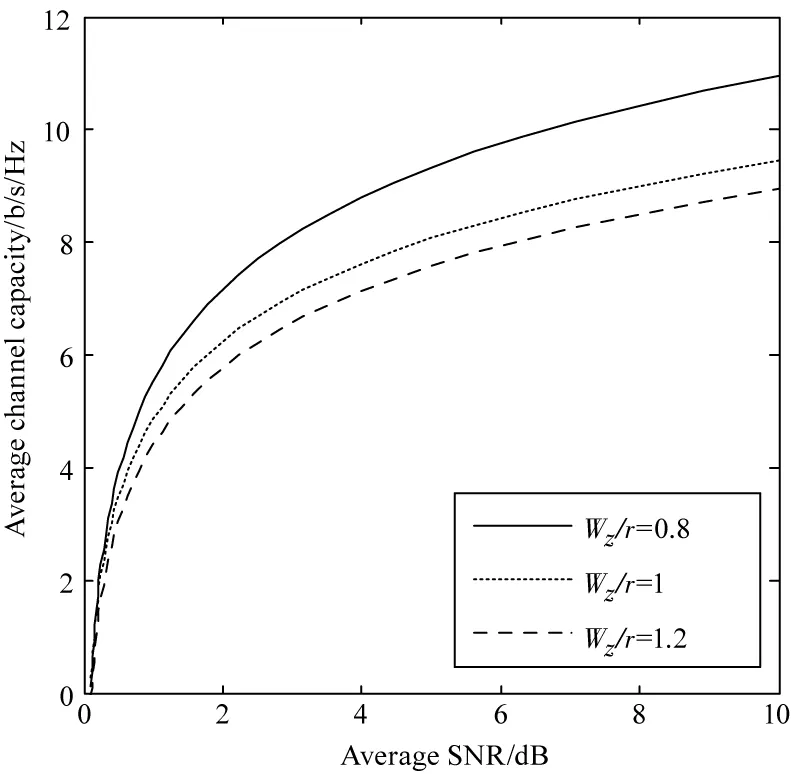
图3 当L=20 km,Cn2=1×10-14,σs/r=0.5时,不同wz/r比值下,平均信道容量随信噪比的变化关系

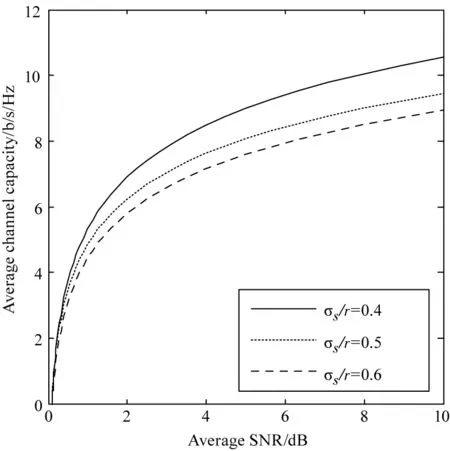
图4 当L=20 km,Cn2=1×10-14,wz/r=1时, 不同σs/r比值下,平均信道容量随信噪比的变化关系

图4为在中湍流强度Cn2=1×10-14,L=20 km,接收端处波束宽度与接收机半径比值为wz/r=1时,在不同接收端处抖动标准差与接收机半径的比值σs/r条件下,平均信道容量与信噪比的关系。从图中可以看出,随着接收端处抖动标准差与接收机半径的比值σs/r增大平均信道容量减小,这是由于σs/r的增大表明指向误差对链路的影响越强,故信道容量越小。在信噪比为6 dB的条件下,当σs/r=0.4时,平均信道容量为9.519,当σs/r=0.5时,平均信道容量为8.532,当σs/r=0.6时,平均信道容量为8.039。所以采取一定的措施减少指向误差对链路的影响,可提高系统的通信性能。由图可知,同一σs/r值下,平均信道容量随着信噪比的增大而增加。

5 结 论

混合RF/FSO通信系统克服了不良天气对通信的影响,提高了系统的可用性。本文研究了混合RF/FSO通信系统平均信道容量受不同参数的影响。其中FSO链路基于Exponentiated Weibull 分布大气湍流衰减模型,考虑联合指向误差及大气衰减因素,推导出平均信道容量的闭合表达式,并根据表达式分别进行仿真分析了不同性能参数对平均信道容量的影响。由仿真分析可知,随着距离增加、湍流强度加强、接收端处波束宽度与接收机半径比值上升、接收端处波束宽度与接收机比值的增加,平均信道容量随之减少,系统性能不断恶化。在实际应用中,可以利用推导的闭合表达式对混合RF/FSO通信系统性能评估提供参考,进行参数优化,改善系统性能。

参考文献:

[1] P Puri,P Garg,M Aggarwal.Outage and error rate analysis of network-coded coherent TWR-FSO systems[J].IEEE Photonics Technol.Lett.,2014,26:1797-1800.

[2] S Zvanovec,J perez,Z Ghassemlooy,e al.Route diversity analysis for free-space optical wireless links within turbulent scenarios[J].Opt.Express,2013,21:7641-7650.

[3] Isaac I Kim,Eric Korevaar.Availability of free space optics and hybrid FSO/RF systems[C].San Diego:SPIE,2001,(4530):84-95.

[4] GUO Lei,QI Weijing,HOU Weigang,et al.FSO/RF communication technology in space information network[J].Science & Technology Review,2016,34(16):76-81.(in Chinese)

郭磊,亓伟敬,候维刚等.空间信息网中的FSO/RF通信技术[J].科技导报,2016,34(16):76-81.

[5] Wang D,Abouzeid A A .Throughput capacity of hybird radio frequency and free space optical(RF/FSO) multi-hop networks,ITA 07,2007：3-10.

[6] Hassan Moradi,Maryam Falahpour,Hazem H.Refai elt.On the capacity of hybrid FSO/RF links[C].IEEE Globecom 2010 proceedings,2010,978-1-4244-5638-3/10.

[7] Liu B,Liu A,Towsley D.On the capacity of hybrid wireless networks[C].IEEE INFOCOM’03,March 2003.

[8] Barris R,Dios F.Exponentiated Weibull distribution family under aperture averaging for Gaussian beam waves[J].Opt.Express,2012,20(12):719-721.

[9] Barris R,Dios F.Exponentiated Weibull model for the irra diance probability density function of a laser beam propagating through atmospheric turbulence[J].Optics & laser technology,2013,45(1)：13-20.

[10] HAN Liqiang,YOU Yahun.Performance of free space optical communication with combined effects from atmospheric turbulence and pointing errors [J].Acta Optica Sinica,2014,34(11):1-6.(in Chinese)

韩立强,游雅晖.大气湍流及瞄准误差联合效应下自由空间光通信的性能[J].光学学报,2014,34(11):1-6.

[11] A A Farid,S Hranilovic.Outage capacity optimization for freespace optical links with pointing errors [J].J Lihgtwave Technol,2007,25(7):1702-1710.

[12] Adamchik V S,Marichev O I.The algorithm for calculating integrals of hypergeometric type functions and its realization in reduce system [C].International Conference on Symbolic and Algebraic Computation,1990:212-2.