百叶风口的对开张角对室内热舒适性及能耗影响分析

刘鹏飞，陈焕新∗，王江宇，雷艳杰，张军，孙策

（1-华中科技大学能源与动力工程学院，湖北武汉 430074；2-北京华誉能源技术股份有限公司，北京 100083）

0 引言

随着社会的快速进步和经济的迅猛发展，人们的经济水平不断提高，这也使得人们对生活环境有了更高水平的要求。现如今，人们的大部分时间都是在室内度过，而室内环境质量的优劣取决于室内气流组织的分布。我国国家标准《采暖通风与空气调节设计规范》[1]规定，舒适空调室内温、湿度参数如下：夏季温度24 ℃～28 ℃，湿度40%～65%，空气流速小于0.3 m/s。

1 模型的建立

1.1 物理模型

本文所研究的空调办公室房间尺寸为5.5 m×4.0 m×3.5 m，中央空调的单层百叶风口位于房间左侧，其尺寸为0.8 m×0.2 m，回风口尺寸0.8 m×0.2 m，办公桌尺寸为2.0 m×1.5 m×0.8 m，书柜紧贴墙壁，对室内气流组织影响较小，故不予考虑，日光灯管由于体积较小，且一般白天不开，故忽略。工作人员两名，大部分时间人员静坐在电脑前，而电脑体积较小，为简化模型，将电脑和人体一同等效为一个长方体，等效尺寸为0.6 m×0.3 m×1.2 m，其热流密度为100 W/m2，整体模型如图1所示。

图1 房间模型图

1.2 风口模型

空调通风房间实际的送风口几何形状很复杂，其入口的边界条件往往难以直接描述。目前描述风口的模型众多，各有优缺点，本文以“N点风口动量模型”为基础，结合“局部定义法”来描述百叶风口。

N点风口动量模型使用N个简单的开口代替不同出流方向，从而简化对入流边界条件的描述，对于N的取值，则需要视出流条件而定。但N点动量风口模型只能实现于清华大学自主开发的三维通用CFD软件STACH-3中，一般的CFD软件或者传统的流体流动数值模拟算法都无法实现[21]。局部定义法则是傅斌在“N点风口动量模型”的基础之上，使用相应的算法，使之能够在商用CFD软件上实现。

在本文中，百叶风口的尺寸为0.8 m×0.2 m，有效面积系数为0.75，出流方向分为两种情况，即N=1和N=3。当N=1时，出流方向角度为0°；N=3时，叶片对开，目前市面上常见的对开角度分别为20°、30°以及45°。图2为典型百叶风口送风示意图。

图2 典型百叶送风口送风示意图

1.3 数学模型

标准κ-ε湍流模型在工程运用上的准确性已经得到了大量的实验验证，精度可靠，且对于大涡模拟等，计算量要小很多[11]。为此需要如下假设：

1）室内空气低速流动，为不可压缩流体且符合Boussinesq假设；

2）流动为稳态流动，在入口处送风射流参数均匀，室内空气物性为定值；

1.2 方法 对照组孕产妇无定期产检，按照个人意愿进行保健措施。观察组孕产妇严格按照下述原则执行孕期保健：①孕产妇早孕期首诊时建立电子孕产妇保健系统档案，并给予孕妇孕产期保健手册；②定期发放相关宣传资料，定期开办孕妇学校及讲座；③制定产检计划，及时发现相关并发症、合并症并给予积极处理；④对胎儿实施监护，了解胎儿宫内生长状况、有无发育畸形等。

3）空调开启时，门窗一般都处于紧闭状态，故不考虑漏风的影响；

4）忽略四周墙壁及室内物体的辐射热，忽略能量方程中由于粘性作用引起的能量耗散。

2 网格划分及边界条件

2.1 网格划分

办公室空调房间送风口为百叶风口，办公室内实际的百叶风口的尺寸为0.8 m×0.2 m，有效面积系数为0.75，所以模型中的百叶风口尺寸为0.60 m×0.15 m。网格质量的高低是影响计算精度的一个重大影响因素，高质量的网格往往能够加快收敛速度，得到更精确的解。本文借助网格划分软件ICEM，采用结构化网格划分计算域，网格质量最低为0.905，网格数量为920,915，图3为网格划分图。

图3 网格划分图

2.2 边界条件的设置

1）入口边界：送风口定义为速度入口，根据《暖通空调送风风速标准》中规定百叶风口的送风速度为2.5 m/s～4 m/s，为了减小吹风感，选取风口颈部的送风速度2.5 m/s，两侧风口的出风速度按照文献[21]中的公式进行计算，室内设定温度为26 ℃，送风温度为23 ℃，方向分别为0°、20°、30°、45°。根据相应的公式计算出湍流强度I为4.20%，湍流粘度比ut/u为86.54。

2）出口边界：回风口定义为自由出流。

3）壁面边界：空调房内壁面边界设为恒温边界，按照如图2所示方位，前面的墙壁由于直接吸收太阳的辐射，温度较高，温度T为309.15 K，后墙靠近走廊，温度T为301.15 K，其余四面墙壁由于和其他空调房间相连，均视为绝热壁面；电脑与人同为热源体，等效热流密度为100 W/m2。办公桌不散发热量，仅作为障碍物处理。

4）计算模型选用标准κ-ε两方程紊流模型，近壁面区域选用标准壁面函数法，采用SIMPLE算法。

边界条件设置完成以后，在空调房间内设立3个监测点，以便观测房间内流场的收敛情况，作为判断收敛的主要依据。3个监测点的坐标分别为：point-1（2.75，2，1.1），point-2（1.25，2，1.1），point-3（4.25，2，1.1）。

3 模拟结果与分析

3.1 室内温度场与速度场分析

由于人体的温度敏感区位于头部和脚踝处，室内人员坐姿时头部的高度约1.1 m，脚踝处高度约为0.1 m。因此，选取这两个截面的温度和速度分布来评判室内的热舒适度。

图4～图7分别为对开角度为0°、20°、30°和45°时室内温度场与速度场的分布情况。

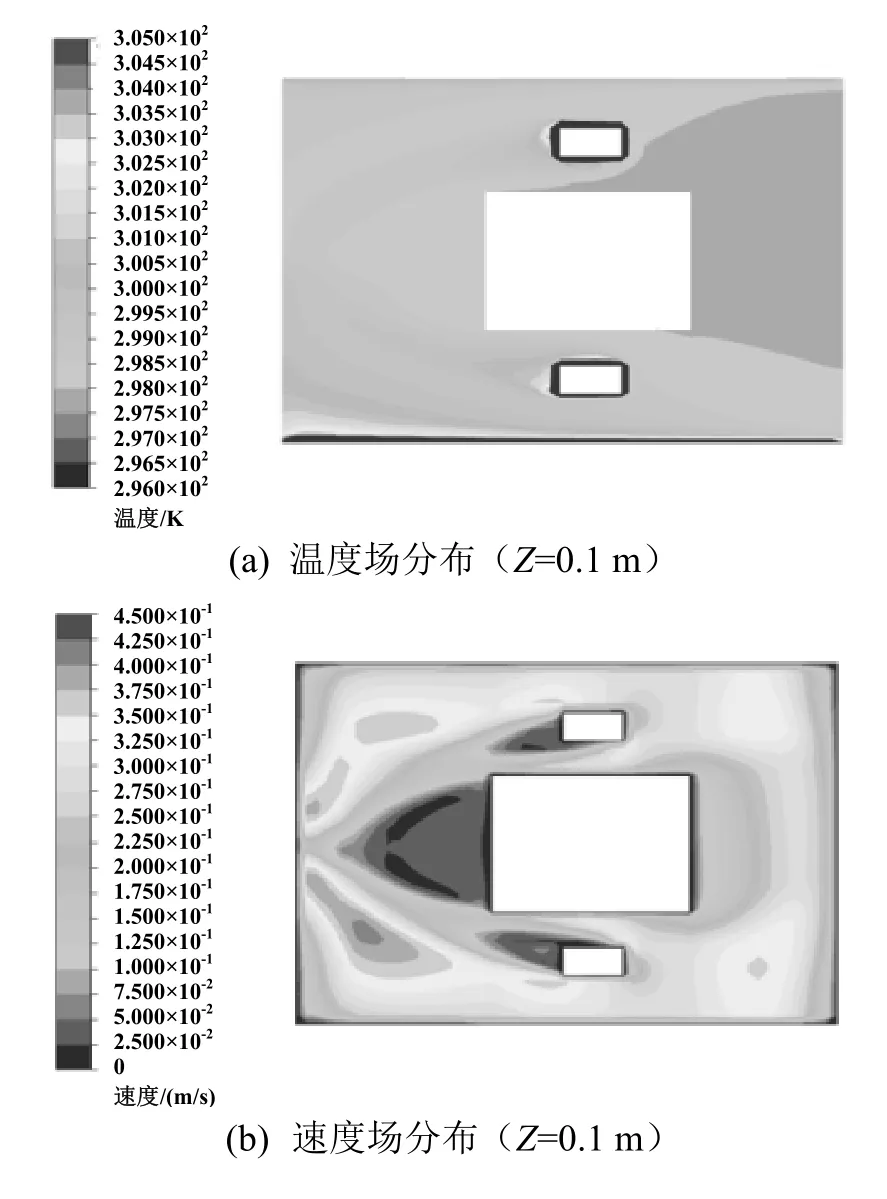
图4 对开角度为0°时温度和速度分布云图

图5 对开角度为20°时温度和速度分布云图

图6 对开角度为30°时温度和速度分布云图

图7 对开角度为45°时温度和速度分布云图

3.2 室内热舒适性评价——PMV评价

预测平均热感觉指标PMV，是丹麦FANGER教授在人体热平衡方程的基础上，通过收集1,396名受试者的冷热感觉资料后，提出的用于评价人体热舒适性的一个数值指标[22]。

ISO以及ASHRAE等组织依据FANGER教授的PMV-PPD指标，规定室内热环境的舒适标准为-0.5＜PMV＜0.5，相应的PPD为PPD＜10%。而我国很多学者认为,上述指标要求太高，在我国大部分地区难以实现，而且亦无必要。所以一般认为可以接受舒适热环境的PMV为-1.0＜PMV＜1.0，相应的PPD小于26%。因此，通过FLUENT中相应的功能，将PMV值超过小于-1或大于1的区域切除。图8为不同对开角度下截面Z=1.1 m处的PMV云图。

观察云图容易发现，对开角度为20°时，截面的PMV值基本上全部位于-1～1之间，并且PMV值分布也较为均匀，在工作人员附近的PMV值大部分位于-0.4～0.4，PMV接近1或-1的区域也很少，热舒适性在水平面上是4种对开角度中是最好的；当对开角度为0°时，左下角有小块区域不符合要求，结合图4(b)的风速分布分析，由于送风口垂直于风口送风，导致左下角和右上角均出现送风死角，而外墙的温度较内墙高，这才导致了左下角的PMV值过大；当对开角度为30°时，靠近外墙的工作人员附近以及外墙附近有一部分不符合；当对开角度为45°时，整体上是符合要求的，但是工作人员附近有小部分区域偏离设定值。

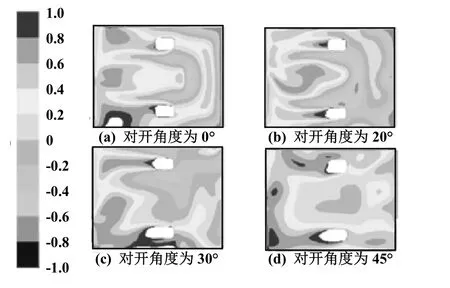
图8 不同对开角度下截面Z=1.1 m处的PMV云图

为进一步分析室内垂直方向上的热舒适性，选取Y=1 m（工作人员附近）截面处的PMV云图进行分析。图9是不同对开角度关于截面Y=1 m处的PMV云图。

观察图9可以看出，在侧送侧回的通风方式下，气流从上部沿直线方向进入室内，部分冷空气从风口进入房间以后，逐渐沉降地面，另一部分冷空气沿着循环路径与室内空气进行换热，然后受热力影响上升到房间上部，形成下部适中，中上部稍暖的空气分层现象。这种现象同样反映到PMV值上，即房间中上部的PMV值高，下面的偏低。并且可以看到，对开角度为20°时，除去接近天花板处的PMV过低之外，其余区域的PMV值的分布是非常均匀的，而天花板附近并不是工作区，所以在垂直方向上同样是20°度最为合理。

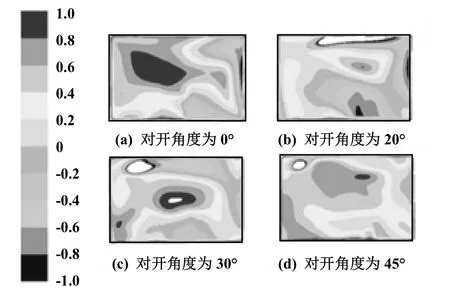
图9 不同对开角度关于截面Y=1 m处的PMV云图

分析对开角度为0°的截面，新风射流从风口进入室内以后，它与周围静止流体之间存在速度不等的间断面，间断面一般会受到不可避免的干扰，从而失去稳定而产生涡旋，卷吸周围流体进入射流，同时不断移动、变形、分裂产生紊动，其影响逐渐向内外两侧发展形成自由紊动的混合层。卷吸和掺混的结果就导致射流断面不断扩大，而流速则不断降低，流量沿程增加。在这期间，部分低温气流向下沉降，较多的气流仍继续沿着原来的方向继续流动，最终撞击到墙壁，致使大部分气流沿墙壁向下流动，沿地板回流至回风口。而工作人员的工作区域偏离中轴面较远，冷空气进入室内后，大部分气流的循环路径都是围绕在中轴面附近，只有少部分气流能够循环经过工作人员上方，吸热有限。而且刚刚从风口出来的射流由于速度较快，冷气流沉降时间有限，气流向下沉降的不多，但射流轴心速度衰减较快，所以后半段的冷空气沉降要比前半段多，这就解释了为何截面左中部的PMV偏高。

3.3 能耗分析

根据模拟的结果，导出4种工况下各壁面的热流量，汇总于表1。

对比4种工况的热流量，可以发现，不同工况下各壁面热流量相差较大。由于4种工况下，只有对开角度不同，其余各条件都是相同的，除了前后壁面有热流的进出，其它四面都是绝热面，没有热流量的进出，所以前后壁面的热流量的高低可以用来定性地分析该房间的能耗。工况二（20°）的热流量是最少的，工况一（0°）热流量最多。这说明，在对开角度为20°的情况下，房间的能耗是最小的，当对开角度为0°时，能耗是最大的。并且可以发现，随着送风角度的变大，总热流量是先减小后增加的，可能在0°～30°下存在一个极小值。

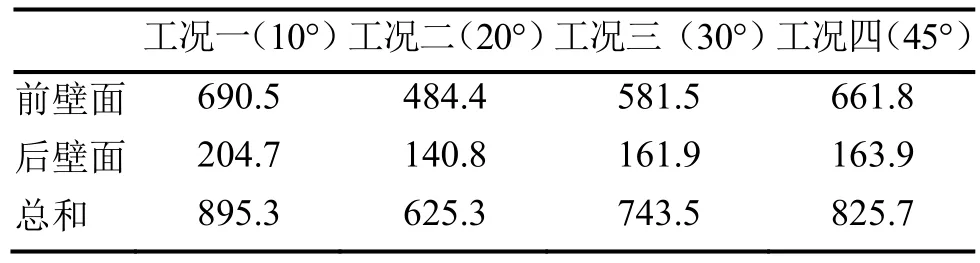
表1 不同工况下壁面的热流量（W）

4 结论

本文通过对夏季一典型办公室内流场进行数值模拟，比较百叶风口在不同对开角度下室内温度场、速度场、PMV分布以及能耗，得出以下结论：

1）通过数值模拟，得到了室内温度场、速度场及PMV热舒适性指标，根据这些指标可以对室内热舒适性进行直观且科学合理的预测和评价；

2）通过定性分析4种工况下的能耗，得出当对开角度为20°时的能耗是最低的。并且发现随着送风角度的变大能耗随之变化的规律，在0～30°，可能存在一个对开角度，使能耗最低；

3）本文通过对比4种工况，对特定模型下室内热舒适性进行比较，得出当对开角度为20°时，室内温度以及速度分布比较均匀，热舒适性是最优的，并且能耗最小。而对于其他的对开角度，或多或少都存在部分区域不符合标准。

由于条件所限，本文未对模拟数据进行实验验证，但本文的模拟结果可以为相关工作人员提供借鉴，为优化室内流组织设计提供了理论依据和科学指导，从而优化室内的气流组织设计。

[1]中华人民共和国建设部. 采暖通风与空气调节设计规范[S]. GB 50019-2003. 北京: 中国建筑工业出版社,2003: 9-20.

[2]DAGHIGH R, SOPIAN K. The impact of air exchange effectiveness on thermal comfort in an air-conditioned office[J]. American Journal of Applied Sciences, 2009,6(11): 1974-1981.

[3]MAJDOUBI H, BOULARD T, FATNASSI H, et al.Airflow and microclimate patterns in a one-hectare Canary type greenhouse: an experimental and CFD assisted study[J]. Agricultural and Forest Meteorology,2009, 149(6):1050-1062.

[4]曹建伟. 置换通风空调室内空气品质的数值模拟研究[D]. 北京: 北京交通大学, 2007.

[5]刘敏, 李明海, 卢明, 等. 空调办公室热环境数值模拟研究[J]. 土木建筑与环境工程, 2015, 37(S1): 28-31.

[6]钟武. 夏季办公室空调房间气流组织的数值模拟[J].制冷与空调, 2011, 25(3): 304-308.

[7]李朝妹, 张振彬. 空调安装位置对办公室室内温度的影响[J]. 建筑节能, 2011, 39(11): 16-18.

[8]孙建丽, 刘秀玉. 基于FLUENT的空调送风角度对房间舒适性及能耗的影响[J]. 建筑节能, 2015, 43(4):21-24.

[9]吴显庆, 钱付平, 阚竟生, 等. 通风方式对室内热舒适性影响的数值模拟[J]. 制冷与空调(四川), 2015, 29(1):16-21.

[10]沈凯, 吴喜平, 宋洁, 等. 某地铁站厅不同送回风方式的气流组织数值模拟和分析[J]. 制冷技术, 2010, 30(1):28-32.

[11]刘天骄, 吴经伟, 臧建彬. 通风格栅类型对高速列车设备舱通风散热特性的影响[J]. 制冷技术, 2017, 37(3):58-62.

[12]俞国华. 变风量空调室内气流组织的数值模拟[D]. 西安: 西安建筑科技大学, 2004.

[13]喻继平, 何媛, 赵玉娇, 等. 基于气流组织CFD优化的某报社印刷车间空调系统设计[J]. 暖通空调, 2012,42(11): 113-118.

[14]申健, 杨长青, 高小攀, 等. 一种新型组合式风口分层空调气流组织形式研究[J]. 建筑科学, 2017, 33(8):83-89.

[15]旷金玉, 罗卓英, 周猛, 等. 百叶风口空调房间室内热环境的数值模拟研究[J]. 科学技术与工程, 2012, 12(2):353-357.

[16]JURELIONIS A, GAGYTĖ L, PRASAUSKAS T, et al.The impact of the air distribution method in ventilated rooms on the aerosol particle dispersion and removal:The experimental approach[J]. Energy and Buildings,2015, 86: 305-313.

[17]赵彬, 李先庭, 彦启森. 置换通风的数值模拟[J]. 应用力学学报, 2002, 19(4): 75-79.

[18]赵彬, 李先庭, 彦启森. 室内空气流动数值模拟的N点风口动量模型[J]. 计算力学学报, 2003, 20(1): 64-70.

[19]赵彬, 李先庭, 彦启森. 室内空气流动的简捷数值模拟方法[J]. 暖通空调, 2003, 33(3): 102-104.

[20]傅斌, 李晓冬. 室内气流数值模拟中对方形散流器送风口的描述方法[C]// 全国暖通空调制冷2002年学术年会资料集, 2002.

[21]娄君. CFD风口模型的研究与应用[D]. 成都: 西南交通大学, 2012.

[22]罗渊, 徐文华. 平均辐射温度对睡眠环境人体热舒适的影响[J]. 制冷技术, 2010, 30(4): 52-56.