变截面风管空调房间气流组织的数值模拟

金莎，沈惬，孙大明∗，张学军

（1-浙江大学能源工程学院，浙江杭州 310027；2-长沙有色冶金设计研究院有限公司，湖南长沙 410000）

0 引言

空调房间的气流组织，是指确定合适的送（回）风口形式、位置、规格、数量和送（回）风风量、风速、温度等参数[1]。这些参数是影响室内的空调效果，关系着房间工作区的温湿度基数、精度及区域温差、工作区的气流速度和清洁程度以及人们舒适感觉的重要因素，成为空气调节和工程设计的重要环节[2]。气流组织分布规律的传统研究采用模型实验方法，但随着计算机技术的发展，利用流体动力学（Computational Fluid Dynamics，CFD）进行数值模拟求解的方法有了很大的发展，它具有成本低、速度快且可模拟各种不同工况等优点[3-6]。

室内孔板送风方式多用于对室内温度、湿度、洁净度和气流分布均匀性有精度要求的空调系统中[7]。国内对孔板送风的研究倾向于孔板送风口研究，赵彬等[8-9]在2002年将N点风口模型用于数值模拟室内空气流动的孔板类风口入流边界条件，其模拟结果与实验数据对比，发现能满足工程上的使用要求，在2003年将N点风口模型应用于采用孔板风口送风的洁净室气流组织模拟，发现模拟结果与实验数据吻合较好，验证了该模型使用的正确性；徐旭等[10]、丁国良等[11]和肖德玲等[12]对圆柱面孔板的阻力特性进行数值模拟，并拟合出其阻力特性随开孔率变化的曲线，得出了圆柱面孔板与平面孔板送风末端兼有的管路流量分配和阻力特性；国外SAMADIANI等[13]和ARGHODE等[14-15]研究了增压管和孔隙率对采用孔板送风的计算机房气流组织影响，并对不同模型的优劣进行研究，发现MBF模型能在保证预测准确前提下减小计算工作量。

为了解孔板对流场的作用及不同送风量下孔板送风流场特征，本文采用CFD方法，对10 m×10 m×4 m的房间气流组织进行有无孔板的对比，以及1倍设计风速和2倍设计风速比较，总结各自不同的气流组织特点，为空调设计提供依据。

1 模型建立

1.1 物理模型

采用fluent前处理软件，对房间尺寸为10 m×10 m×4 m进行建模，模型一为有孔板的空调房间物理模型，孔板在高度为3 m处，如图1所示。模型二为无孔板的空调房间物理模型。其中风管各截面面积分别为0.45 m×0.45 m、0.4 m×0.4 m、0.32 m×0.32 m和0.22 m×0.22 m，风管布置于房间的中间，将风口布置于风管的两侧，风口面积分别为0.45 m×0.3 m、0.4 m×0.3 m、0.32 m×0.3 m和0.22 m×0.3 m，且3个回风口分布在回风墙上，面积为0.6 m×1.0 m。

1.2 边界条件设置

对模型的边界条件设置进行如下假设：

1）传热计算主要考虑流体的内部传热，外表面传热均设定为恒热流；

2）房间内空气流动为稳态的湍流流动，相应选用κ-ε湍流模型进行模拟；

3）房间内空气为不可压缩气体，且认为密度是恒定值；

4）送风口为射流参数均匀的速度入口，回风口为自由出流；

5）假设空气的湿度对室内气流组织无影响；

6）孔板层采用porous-jump边界条件。

图1 物理模型示意图

2 模拟结果分析

房间送风量按换气次数计算，一般采用的换气次数为(8～12)次/h，本文选择10次/h为设计工况，因此设计送风量为4,000 m3/h，实际中通过末端调节阀来控制每个风口的出风量，以保证每个送风口风量一致，各风口的速度入口条件根据各送风口的面积计算得出。分析时，以离孔板0.5 m的两个平面z=2.5 m和z=3.0 m进行风速均匀性比较，并统计了高度方向2.5 m～3.5 m间隔0.1 m的每个平面的面平均风速，以了解孔板前后速度变化情况。

模拟中采用的送风孔板厚度为dx为0.01 m，孔隙率Φ为25%，其压力跳跃系数C2为3,902，采用如下公式(1)[16]计算：

式中：

dx——送风孔板厚度，m；

C2——压力跳跃系数，m-1；

φ——孔隙率。

本文对气流组织的评价采用均匀性系数δ[17]，它是在概率统计中反应组内个体间离散程度的速度标准差与面平均速度的比值，值越小，说明流场速度之间的差别越小，流场均匀性越好，计算公式如式(2)：

式中：

δ——均匀性系数；

vi——速度，m/s；

——面平均速度，m/s。

2.1 模型一在设计风量下的模拟结果分析

模型一在设计风量条件下平面z=2.5 m和平面z=3.5 m处的速度矢量图，如图2所示。从图中可以看出，平面z=3.5 m的速度场受到送风口影响，其速度存在一些局部速度较大的区域，造成该平面的均匀性差，而平面z=2.5 m的速度场因经过孔板层，相比于平面z=3.5 m的均匀性有一定程度的提高。利用均匀性系数对该平面的均匀性进行分析，可以得到平面z=2.5 m处的δ值为0.233，平面z=3.5 m处的δ值为0.395，由此可见，经过孔板之后，风速均匀性提高了0.162。

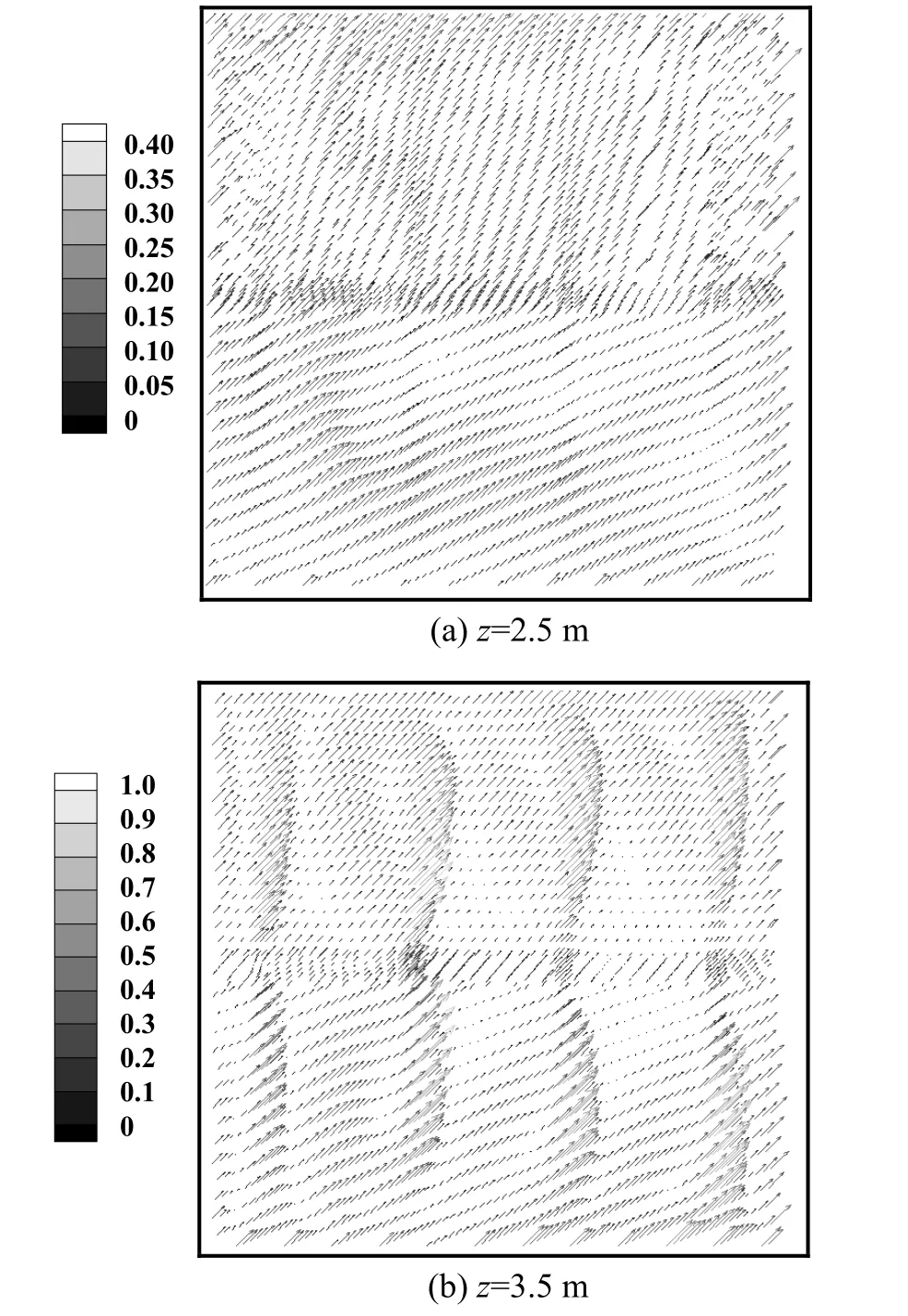
图2 平面z=2.5 m和平面z=3.5 m的速度矢量图

2.2 模型一在2倍设计风量条件下的模拟结果分析

模型一在2倍设计风量条件下平面z=2.5 m和平面z=3.5 m处的速度矢量图，如图3所示。从平面z=3.5 m的矢量图可以看出，该平面存在明显的回流，而平面z=2.5 m的速度场因经过孔板层，相比于平面z=3.5 m的均匀性有一定程度的提高，但相比较于设计风量都有一定程度下降。利用均匀性系数对该平面的均匀性进行分析，可以得到平面z=2.5 m处的δ值为0.259，平面z=3.5 m处的δ值为0.534，由此可见，经过孔板之后，风速均匀性提高了0.275，且提高程度较设计风量的0.162大。

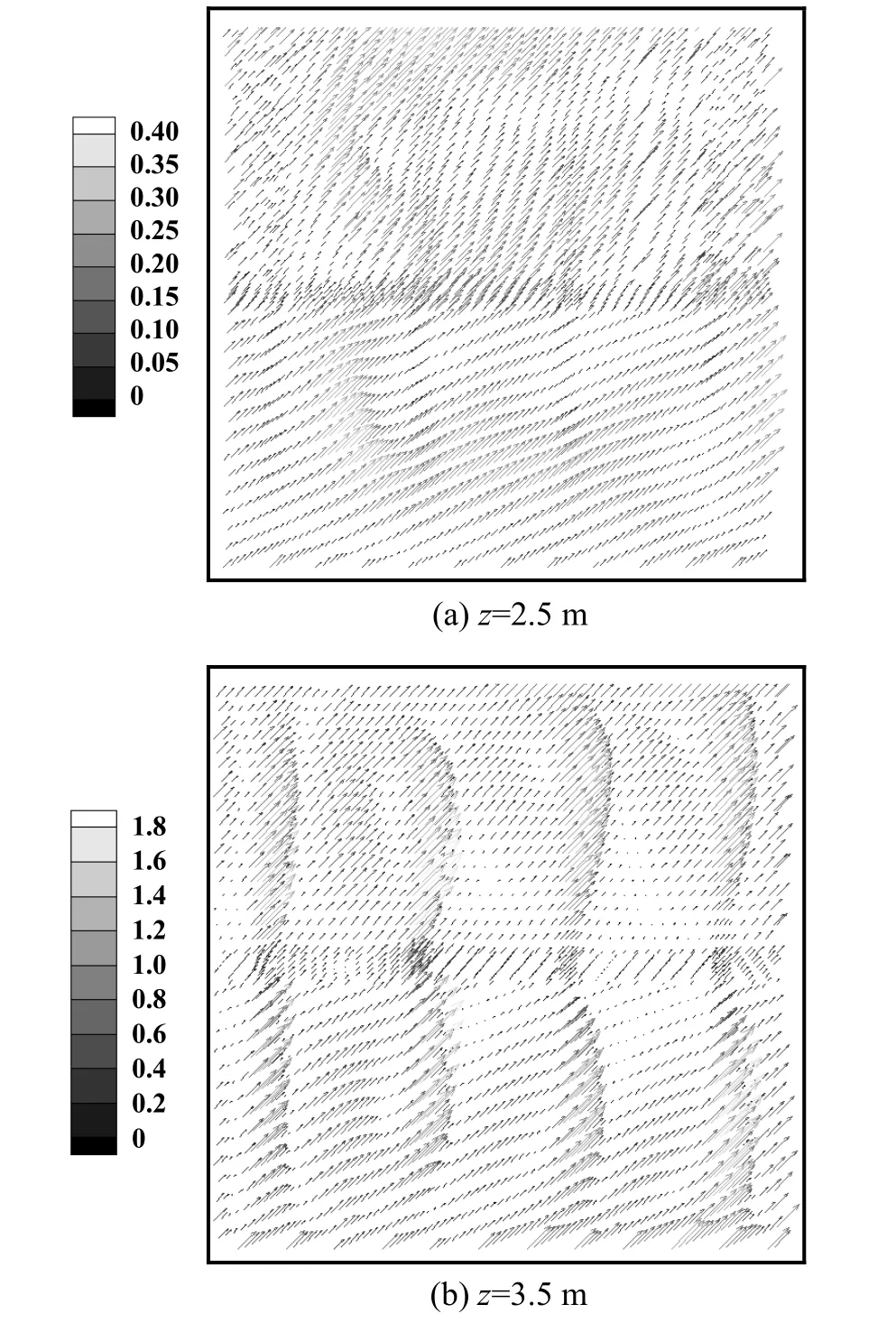
图3 平面z=2.5 m和平面z=3.5 m的速度矢量图

2.3 模型二在设计风量下的模拟结果分析

模型二在设计风量条件下平面z=2.5 m和平面z=3.5 m处的速度矢量图，如图4所示。从平面z=3.5 m的矢量图可以看出，该平面在墙壁附近存在明显的回流，平面z=2.5 m也在靠近墙壁处有明显的回流，但其流场均匀性较平面z=3.5 m处好。利用均匀性系数对该平面的均匀性进行分析，可以得到平面z=2.5 m处的δ值为0.414，平面z=3.5 m处的δ值为0.454，因没有孔板，平面z=2.5 m处的流场均匀性比有孔板存在的情况要差，而与平面z=3.5 m相比，其均匀性比差别较小，仅差0.04，这是因为平面z=2.5 m处的速度密集程度比平面z=3.5 m处要好，但面平均速度较平面z=3.5 m处小。

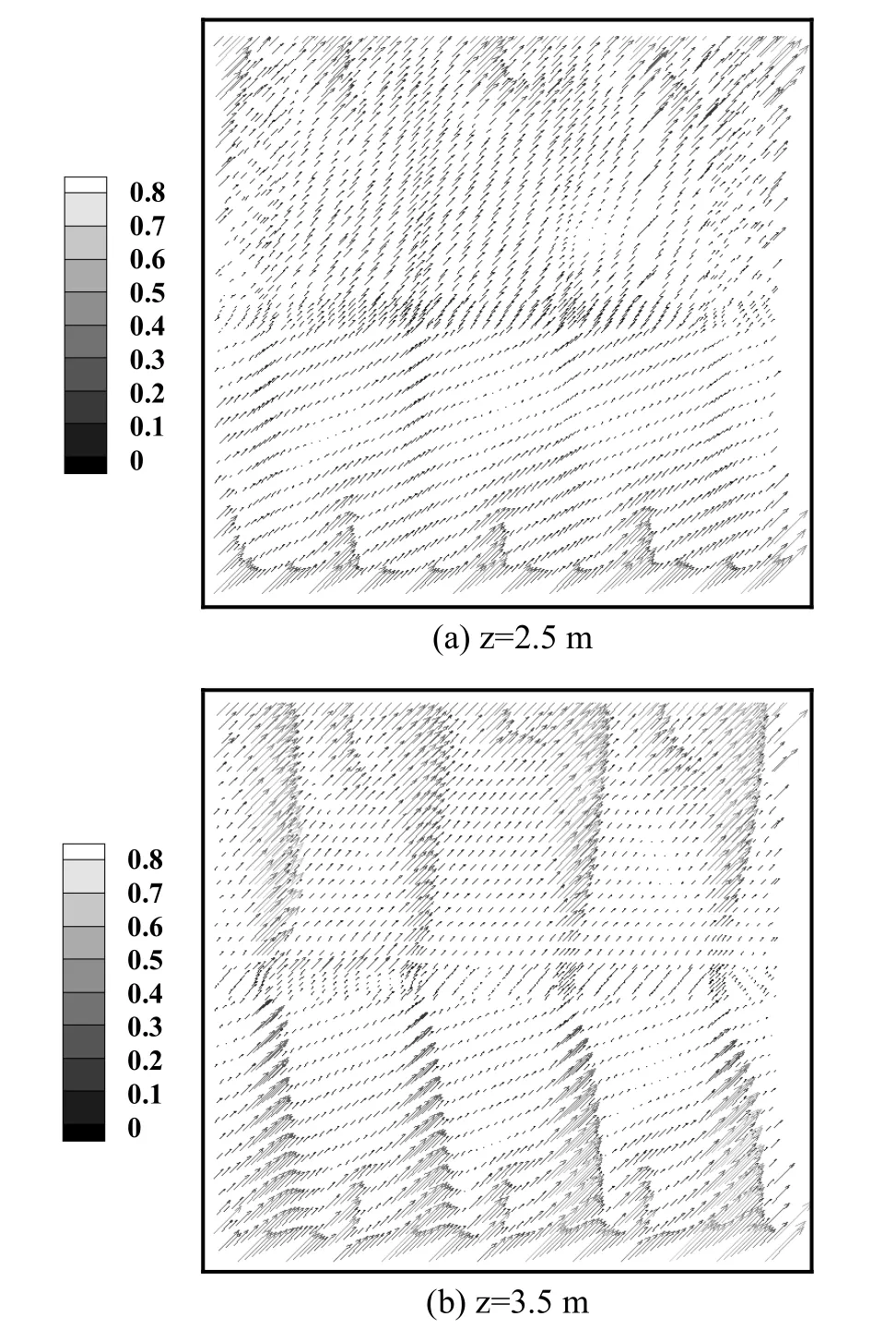
图4 平面z=2.5 m和平面z=3.5 m的速度矢量图

2.4 模拟结果对比分析

各模拟条件下孔板附近的面平均速度变化情况，如图5所示。图中可以看出无孔板的变化曲线比较平缓，而有孔板存在时会在孔板层位置的速度斜率存在较大的变化，使得孔板上部区域的面平均速度较大、下部区域的面平均速度较小，有利于消除下部工作区域由于风速太大带来的“吹风感”等不利因素。孔板的这种作用是因为它能对气流产生一定的阻力，存在压降，使得速度衰减较快，从图中还可以看出，送风速度越大，阻挡作用越明显。

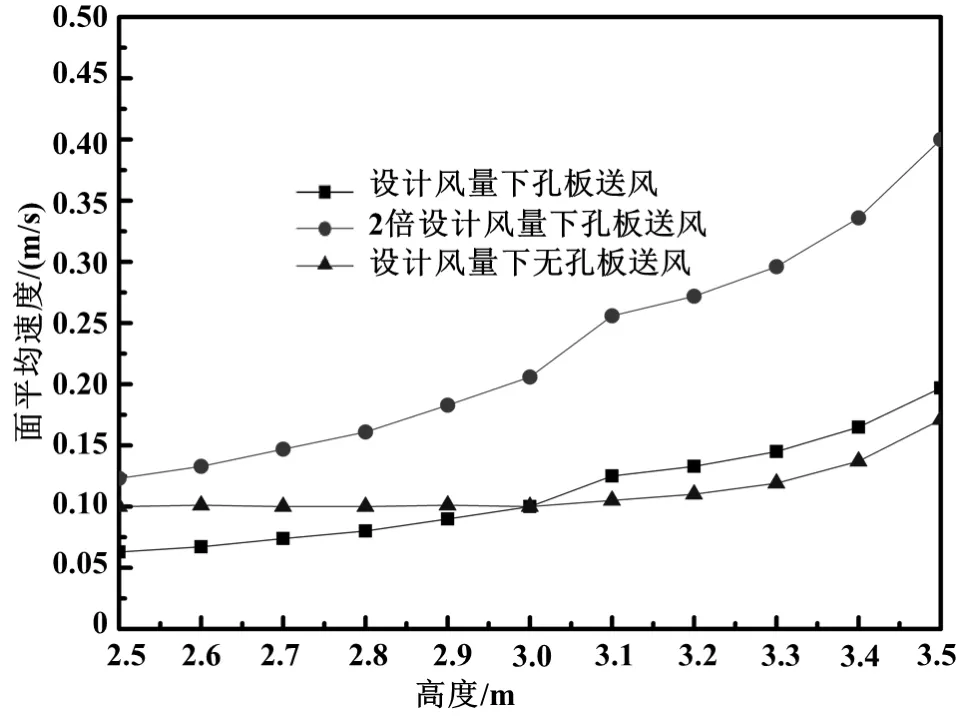
图5 各模拟条件下孔板附近平面的面平均速度

3 结论

孔板通过其阻挡作用，增加上部区域气体速度，降低下部气体速度来改善流场均匀性。本文通过对空调房间是否采用孔板及采用不同送风量情况进行模拟，可以知道孔板确实可以提高空调房间流场的均匀性，且随着送风量的增大，孔板层的作用越明显。由此可知，在设计中，对于流场均匀性要求较高且送风量较大的场合宜采用孔板送风的送风方式。

[1]袁东升, 田会玲, 高建成. 气流组织对空调房间空气环境影响的数值模拟[J]. 建筑节能, 2008(9): 9-13.

[2]梅启元. 空调房间气流组织的数值计算与模拟[D]. 南京: 南京理工大学, 2002.

[3]杜立春. 空调房间气流组织的优化研究[D]. 淮南: 安徽理工大学, 2004.

[4]胡平放, 蔡芬. 气流组织形式对室内空气环境影响的数值模拟[J]. 华中科技大学学报, 2006, 23(2): 28-31.

[5]张欢, 宋国军, 王志刚, 等. 空调房间开机状态温度场动态特性CFD模拟及实验研究[J]. 制冷学报, 2005,26(3): 16-21.

[6]周艳蕊, 俞炳丰, 赵蕊. 空调器送风参数对房间速度场和温度影响的计算模拟和试验研究[J]. 制冷与空调,2004, 4(3): 36-41.

[7]王来. 孔板送风静压箱静压分布规律的实验研究[J].制冷学报, 1991, 12(3): 10-16.

[8]赵彬, 李先庭, 彦启森. 空调孔板风口送风射流的数值模拟[J]. 力学与实践, 2002, 24(1): 18-21.

[9]赵彬, 曹莉, 李先庭. 洁净室孔板型风口入流边界条件的处理方法[J]. 清华大学学报, 2003, 43(5): 690-692,697.

[10]徐旭, 张旭. 多孔板送风末端流量与管路阻力特性的数值模拟[J]. 制冷技术, 2009, 29(2): 34-37.

[11]丁国良, 张春路. 基于模型的制冷空调装置智能仿真[J]. 制冷技术, 2001, 21(4):18-21

[12]肖德玲, 袁琪, 岳锐. 多维送风对空调的舒适性及能耗影响实验研究[J]. 制冷技术, 2011, 31(4): 21-22.

[13]SAMADIANI E, RAMBO J, JOSHI Y. Numerical modeling of perforated tile flow distribution in a raised-floor data center[J]. Journal of Electronic Packaging, 2010, 132(2): 1-8.

[14]ARGHODE V, JOSHI Y. Modeling strategies for air flow through perforated tiles in a data center[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2013, 3(5): 800-810.

[15]ARGHODE V, JOSHI Y. Rapid modeling of air flow through perforated tiles in a raised floor data center[C]//14th IEEE ITHERM Conference, 2014: 1354-1366.

[16]王柳. 地铁客车空调送风风道及客室内气流组织优化研究[D]. 武汉: 华中科技大学, 2008.

[17]陈瑶, 张学军, 陆军亮, 等. 径向流吸附器流体流动特性及其结构参数优化[J]. 化工学报, 2014, 65(9):3395-3402.