一类偏差变元二阶脉冲奇异边值问题正解研究

王凤英，陈铃 ，李秀珍

（山东建筑大学 理学院，山东 济南250101）

0 引言

抽象空间的常微分方程理论是微分方程理论的一个重要分支，其在许多应用领域都有广泛的应用［1-9］。目前，已有研究者对抽象空间中的微分方程的理论进行研究。刘衍胜、李海燕分析了Banach空间中一类奇异脉冲微分方程边值问题多个正解的存在性，并且研究了一类奇异泛函微分方程边值问题的多重正解［10-12］；汪会民等研究了二阶非线性脉冲泛函微分方程正解的存在性［13］；景冰清等证明了一类二阶脉冲微分方程边值问题正解的存在唯一性［14］。但是对有偏差变元的脉冲泛函奇异边值问题的研究较少。因此，文章利用锥压缩及锥拉伸不动点定理，讨论了Banach空间中一类具有偏差变元的奇异脉冲泛函微分方程边值问题多个正解的存在性，并通过例子验证其应用的可行性。

1 偏差变元二阶脉冲奇异边值问题描述

令（E，‖·‖）是实巴拿赫（Banach）空间，设J＝［0，1］，0＜t1＜… ＜tm＜1，PC［J，E］＝｛x｜x：J→E，x（t）在 t≠ tk连续，在 t＝tk左连续且右极限存在，k＝1，2，…，m｝，PC1［J，E］＝｛x｜x∈PC［J，E］并且x′∈PC［（0，1），E］｝，J0＝［0，t1］，Jk＝（tk，tk＋1］，k＝1，…，m，tm＋1＝1。可知PC［J，E］关于范数 ‖x‖PC＝为一 Banach空间。

令E中的一个锥为P，引入偏序关系“≤”，当且仅当y-x∈P时有x≤y，类似地，在PC［J，E］中引入偏序关系，当且仅当 ∀t∈ J，x（t）≤ y（t）时有 x，y∈ PC［J，E］，x≤ y。

研究一类具有偏差变元的二阶脉冲奇异边值问题正解的存在性，其由式（1）［10-11］表示为

式中：f（t，x）有可能在 t＝0及 t＝1处有奇异性；a∈ C［J，R＋］并在（0，1）上 a（t）＞0；R＋＝［0，＋∞）；f∈ C［（0，1）×P，P］；Ik∈ C［P，P］，k＝1，2，…，m；θ是 E的零元。

式（1）的解x指x∈PC［J，E］，ax′∈PC1［（0，1），E］且x满足式（1），正解指非负并且不是平凡解，也就是 x∈ PC［J，P］并且 x（t）不恒等于 θ，t∈ J。

2 偏差变元二阶脉冲奇异边值问题正解的存在性

2.1 预备知识

令 x（t）：（0，1］→E是连续的，若存在，就称积分收敛。同样可定义其它广义积分的敛散性。

设 Tr＝｛x∈E：‖x‖≤r｝，Br＝｛x∈PC［J，E］：‖x‖PC≤r｝（r＞0），D⊂PC［J，E］，D（t）＝｛x（t）：x∈ D｝⊂ E，t∈ J，α是 Kuratowskii非紧性测度［1-3］。

引理（a） 令D⊂PC［J，E］有界并且在每一个集合 Jk（k＝0，1，…，m）上等度连续，则有 α（D）＝

引理（b） 令 P是 E中的一个锥，Pr，s＝｛x∈ P：r≤ ‖x‖ ≤ s｝并且 s＞r＞0。令A：Pr，s→ P是严格集压缩算子且满足下列2点之一，

（1）若x∈P，‖x‖ ＝r有Ax≤／x并且若x∈P，‖x‖ ＝s有Ax≥／x；

（2）若x∈P，‖x‖ ＝r有Ax≥／x并且若x∈P，‖x‖ ＝s有Ax≤／x；

则A在锥P中存在一个不动点x满足r＜‖x‖ ＜s［15］。

2.2 基本假设

（H1）‖f（t，φ（t））‖ ≤ g（t）‖h（φ（t））‖，t∈ （0，1），φ（t）∈ P；其中，g：（0，1）→ （0，∞）是连续的，h：P→P连续有界并且单调递增且 φ（0）＝0，φ（1）＝1。

（H2）对于（H1）中的 h（x）有

式中：N是P的正规常数，P为正规锥

（H′2）把（H2）中的‖x‖→＋∞换为‖x‖→0，其余不变。

（H″2）有 d ＞0使其中如同（H1）所述。

（H3）∀R＞0和［a，b］⊂ （0，1），f在［a，b］×TR上一致连续。

（H4）有常数L≥0，Lk≥0使得∀t∈（0，1）及有界集D⊂P都有 α（f（t，D））≤Lα（D），α（Ik（D））≤Lkα（D），k＝1，2，…，m；且

（H）有（P*是锥P的对偶锥）满足：x＞θ时＞0，且存在a*、b*使得t＜a*＜b*＜1，

5m对于t∈J*＝［a*，b*］一致成立其中

（H′5）把（H5）中的‖x‖→0换为‖x‖→＋∞，其余不变。

2.3 引理及证明

2.3.1 引理1及证明

引理1 当且仅当x是脉冲积分算子，由式（2）表示为

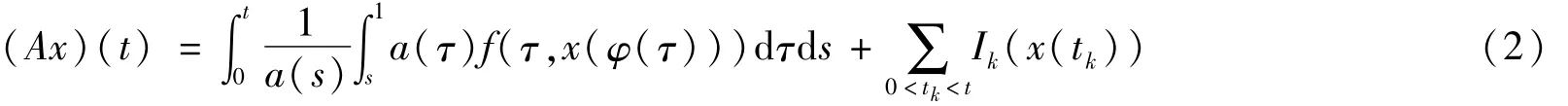
在 PC［J，P］中的不动点时，x∈ PC［J，P］是式（1）的非负解。

证明（略）

2.3.2 引理2及证明

引理2 若（H1）、（H4）成立，则有 ∀r＞0，算子 A：PC［J，P］∩ Br→ PC［J，P］是连续有界的。

证明 由（H4）可知，Ik把 P中的有界集映射成有界集。由（H1）可知，A为PC［J，P］∩Br到PC［J，P］的有界算子。

证明 A是 PC［J，P］∩ Br到 PC［J，P］的连续算子。令｛xn｝，｛x｝⊂ PC［J，P］∩ Br，‖xn-x‖PC→0（n→＋∞）要证明‖Axn-Ax‖PC→0（n→＋∞）。

由（H1）可知｛（Axn）（t）｝在 Jk（k＝1，2，…，m）上等度连续，再由勒贝格控制收敛定理知

‖（Axn）（t）-（Ax）（t）‖Ik（x（tk））‖ →0（n→＋∞）。由 Ascoli-Arzela定理得｛Axn｝在 PC［J，P］中相对紧。

证明 ‖Axn-Ax‖PC→0（n→＋∞）。如果不成立，则有 ε0＞0及｛xni｝⊂ ｛xn｝使得 ‖Axni-Ax‖PC≥ε0（i＝1，2，…）。因｛Axn｝相对紧，所以存在｛Axni｝的子列在 PC［J，P］中收敛到某 y∈ PC［J，P］。不妨设也就是则有 y＝Ax，矛盾。所以，A是 PC［J，P］∩ Br到 PC［J，P］的连续算子。

2.3.3 引理3及证明

引理3 若（H1）、（H3）、（H4）成立，则有∀R＞0，A是PC［J，P］∩Br到PC［J，P］的严格集压缩算子。

证明 令∀R＞0，S⊂PC［J，P］∩BR，由（H1）得AS是有界集并在Ji上等度连续，由引理（a）得式（3）为

式中：（AS）（t）＝｛（Ax）（t）：x∈ S｝，t∈ J。

用格林函数把式（2）改写成式（4）为

式中：G（t，s）

设D

由（H1），对 ∀x∈ S得式（5）为

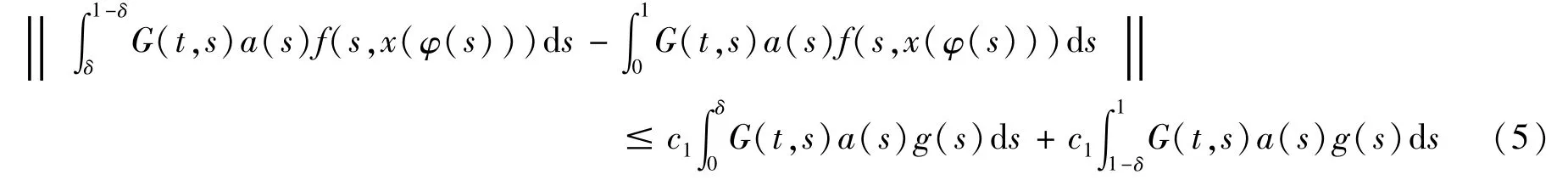
式中

由（5）式及（H1）得 D和 Dδ的 Hausdorff距离 dH（Dδ，D）→0（δ→0＋）。所以，得到式（6）为

估计α（Dδ）。由得式（7）为

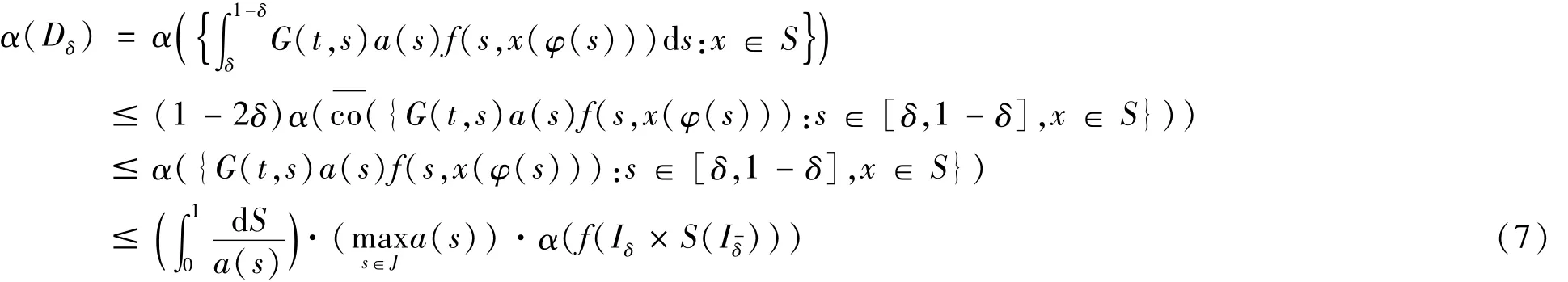
式中

algorithm,while point collection Obis defined to store the intermediate points of the optimized one.The expressions for sets Oaand Obare

再由（H3）、（H4）和式（1）易证式（8）为

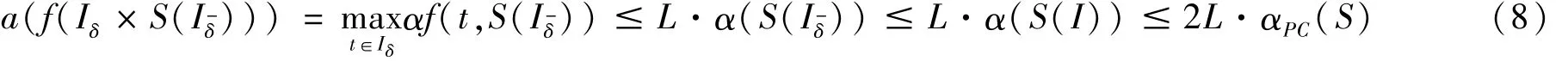
式中：S（I）＝｛x（t）：t∈ J，x∈ S｝

再由式（7）、（8）可知，α（Dδ）≤2LαPC（S）。

设 δ→0＋，结合式（6）得

显然

由式（3）、（8）得 αPC（AS）

由（H4）和引理（b）可得A是PC［J，P］∩Br到PC［J，P］的严格集压缩算子。

2.4 偏差变元二阶脉冲奇异边值问题正解的存在性定理及证明

2.4.1 定理1及证明

证明 由式（4），设由（H1）和（H5）得0＜c*＜1。从 G（t，s）的构造得式（9）为

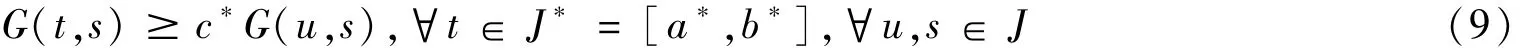
设 K＝｛x∈ PC［J，P］：x（t）≥ c*x（s），∀t∈J*，s∈ J｝。则 K是 PC［J，E］的一个锥，并且 K⊂ PC［J，P］。对 ∀x∈ K，t∈ J*及 ∀u∈ J，由式（4）、（9）得式（10）为

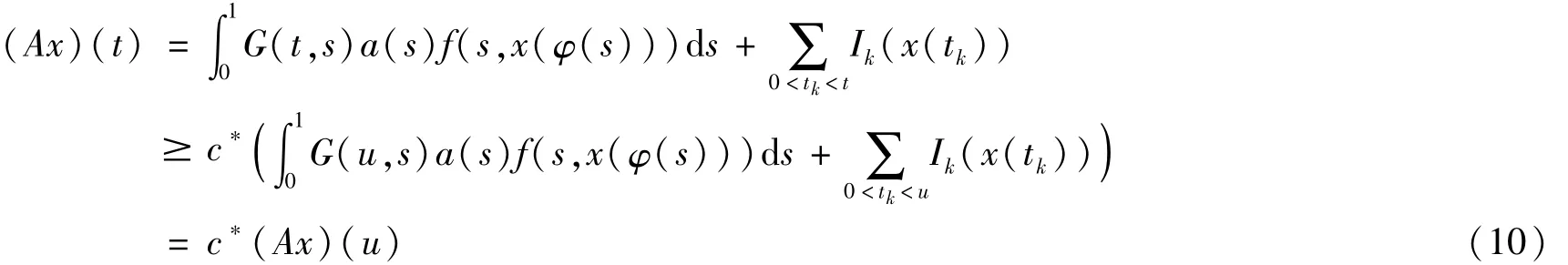
故 A（K）⊂ K。

接下来证A在锥K中满足引理2。

由式（2），结合（H2）有 c′＞c，c′k＞ck满足式（11）为

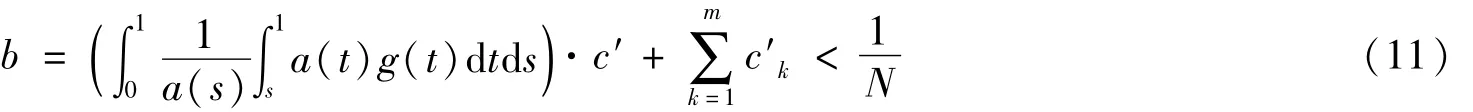
并且由r＞0，当x∈P且‖x‖ ＞r时，得式（12）为

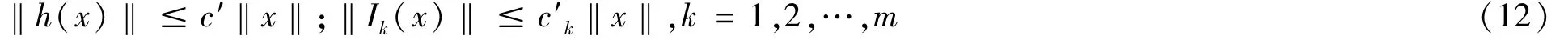
这样，对∀x∈P，得式（13）为

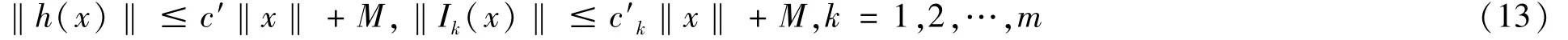
式中＝1，2，…，m）。

设＝1＋（1-Nb）-1NG，其中

事实上，如果有，则得式（14）为满足Ax*≥x*，则有

由 （H1） 和的 取 法 知矛盾，所以式（14）成立。

又由（H5）可知，存在ε＞0，满足式（15）为

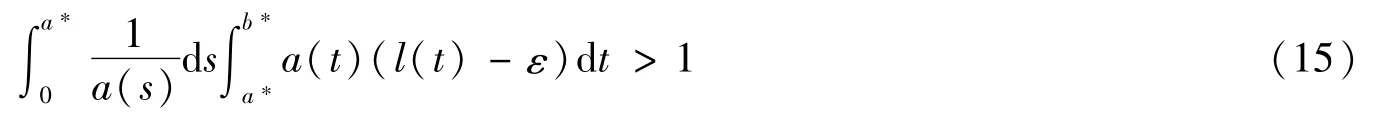
从而存在l＞0，0＜使得当x∈Tr1∩P并且x不恒等于θ时，有式（16）为

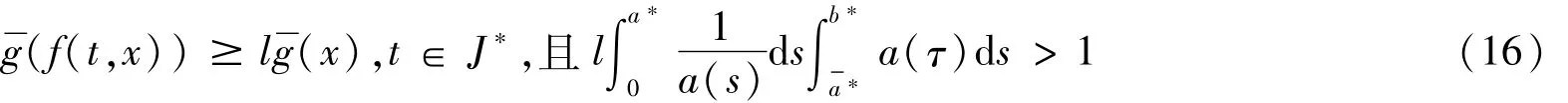
因此，根据式（16）可以证明式（17）成立。

如果有 x0∈ K，‖x0‖PC＝r1满足 Ax0≤ x0，则对 ∀t∈ J*及 ∀s∈ J有 x0（t）≥ c*x0（s），所以，满足式（18）为

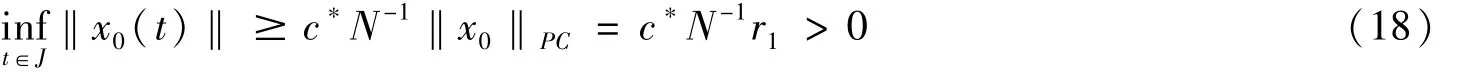
因为a*＝，b*＝由φ的单调性和上述性质得式（19）为

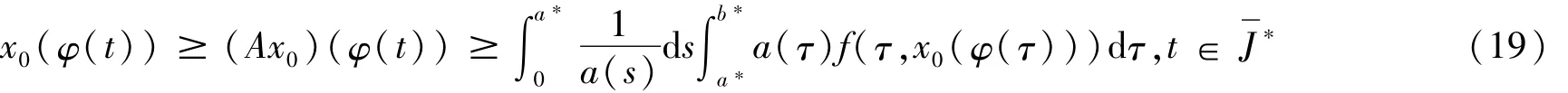
结合式（16）、（19）可知，当 t∈时

因为 x0（φ（t））在上连续（x（φ（t）））在上也连续，所以能取到最小值。由式（18）和（H5）中对的要求可知由式（15）即得矛盾，所以式（17）成立。从而由式（14）、（17），再结合引理（b）即得定理1的结论。

2.4.2 定理2及证明

定理2 如果（H1）、（H′2）、（H3）、（H4）、（H′5）成立，则式（1）至少有一正解。定理2的证明和定理1的证明类似，略。

2.4.3 定理3及证明

定理 3 如果（H1）、（H″2）、（H3）、（H4）、（H5）、（H′5）成立，则式（1）至少有 2个正解 x1、x2满足0＜‖x1‖PC＜d＜‖x2‖PC。

证明 构造与定理1的证明中一样的K，类似地有式（10）成立。

下证（H″2）中的 d由式（20）表示为

如果存在x*∈K，‖x*‖PC＝d使得Ax*≥x*，则有

由（H″2）可知d，矛盾，所以式（20）成立。

由于（H5）、（H′5）成立，和定理1后半部分的证明一样，有0＜r1＜d＜r2使得对∀x∈K，‖x‖PC＝r1，或 ‖x‖PC＝r2时，都有Ax≤／x成立。

连续两次使用引理（b）可得定理3的结论。

3 算例验证

无穷微分方程组由式（21）表示为

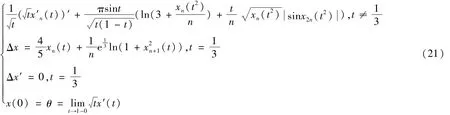
在有界数列组成的抽象空间l∞中考虑此问题，x＝（xn）∈l∞，设‖x‖ ＝sup｜xn｜，则l∞为Banach空间。取P＝｛（xn）：xn≥0，n＝1，2，…｝，则有P是l∞的正规锥，并且正规常数是1。将此问题看成形如式（1）的问题，可取也就是只有一个脉冲点t1＝13，I1（x）＝（Iln（x）），Iln（x）＝45xn＋1ne13ln（1＋x2n＋2）。

验证此函数满足（H1）～（H5）。

取可看出（H1）满足。

因为，所以（H2）也满足。另外显然（H3）成立。

由对角线法则抽取子列的方法得（H4）中的，即（H4）成立。

验证（H5）满足。令 x∈ P，取∈P*满足

则当x＞θ时＞0。

取得到

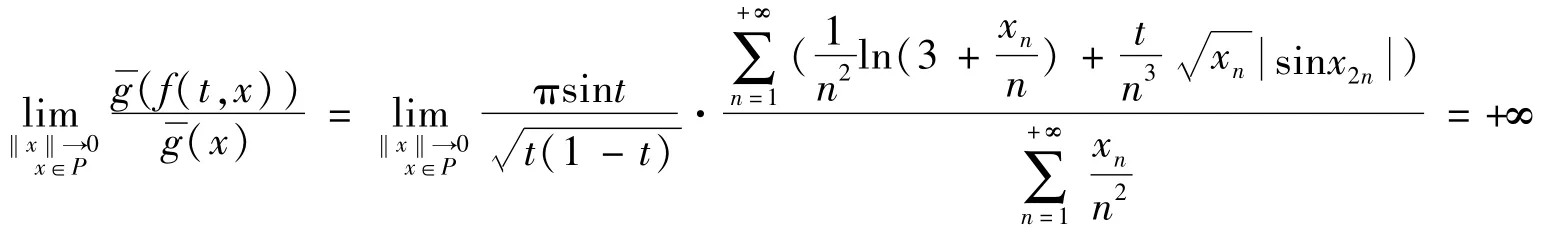
对 t∈ ［a*，b*］一致成立，即（H5）是满足的。

综上可知（H1）～（H5）是成立的，由定理1可知式（21）至少存在一个正解。

4 结语

具有偏差变元的脉冲奇异边值问题是抽象空间常微分方程中一个既有深刻理论意义又有广泛应用价值的研究方向。针对带有偏差变元的抽象微分方程的研究比较少见，因此文章研究的问题有一定的研究价值并且带有挑战性，明确给出了所研究方程多个正解存在的充分条件，具有一定的参考价值。但是文章仅仅给出了一类具有偏差变元的二阶脉冲奇异边值问题正解存在性的充分条件，对于一般的具有偏差变元的n阶脉冲奇异边值问题正解存在性研究将是今后一个重要的研究方向。

［1］郭大钧，孙经先.抽象空间常微分方程［M］.济南：山东科学技术出版社，1989.

［2］郭大钧.非线性泛函分析［M］.济南：山东科学技术出版社，1985.

［3］Guo D J，Lakshmikansham V，Liu X Z.Nonlinear Integral Equations in Abstract Spaces［M］.Dordrecht：Kluwer Academic Publishers，1996.

［4］Agarwal R P，Regan D.Singular boundary value problemes［J］.Nonlinear Analysis，1996，27：645-656.

［5］Agarwal R P，Regan D.Nonlinear superlinear singular and nonsingular second order boundary value problemes［J］.Journal of Differentional Equations，1998，143：60-95.

［6］庞常词.四阶两点边值问题的正解［J］.山东建筑大学学报，2009，24（4）：337-341.

［7］赵庆利，李宗成.均匀棒纯纵向运动方程初边值问题的有限元方法［J］.山东建筑大学学报，2010，25（2）：129-133.

［8］王继忠，于江波，张长学.一类不确定非线性系统的鲁棒调节控制［J］.山东建筑大学学报，2016，31（6）：593-598.

［9］程建刚.一类带奇异性的两点边值问题［J］.数学物理学报，2000，20（1）：109-114.

［10］刘衍胜.Banach空间中一类奇异脉冲微分方程边值问题多个正解的存在性［J］.系统科学与数学，2003，23（2）：215-222.

［11］刘衍胜.奇异泛函微分方程边值问题的多重正解［J］.应用数学学报，2003（4），605-611.

［12］李海燕.抽象空间中二阶奇异脉冲微分方程边值问题的多个正解［J］.安庆师范学院学报（自然科学版），2009，15（1）：21-23.

［13］汪会民，蒋威.二阶非线性脉冲泛函微分方程正解的存在性［J］.巢湖学院学报，2010，12（6）：528-531，547.

［14］景冰清，杨晨.一类二阶脉冲微分方程边值问题正解的存在唯一性［J］.中北大学学报，2013，34（5）：1-5.

［15］韦忠礼.负指数Emden-Fowler方程奇异边值问题的正解［J］.数学学报，1998，41（3）：655-662.