基于隐马尔科夫链的医暴舆情热度分析

秦 旺 赵欣琦 杨媛媛

南京邮电大学 江苏 南京 210000

近年来，暴力伤医事件频发，据中国医院协会最新调查表明，每年每所医院发生的平均数为27.3次。愈演愈烈的医暴事件，不仅使得医生的个人安全遭受巨大威胁，也严重影响社会的和谐稳定。与此同时，随着微博等互联网新媒体平台的崛起，为公共事件提供了强大的舆论阵地，使得医暴事件传播速度加快，辐射范围扩大，迅速形成突发医暴网络舆情。医暴网络舆情使得不实言论快速传播，个体极端情绪迅速放大，进一步恶化了医暴事件的负面影响，激化社会潜在矛盾。

一般认为，舆情热度是舆情的关键指标之一。医暴事件的舆情热度不仅与医患双方本身情况具有强相关联系，在演变过程中，公众的情感强度对其发展的影响同样非常显著。公众对医暴事件的高情感强度将产生助推作用，显著提高舆情事件热度增量值与峰值。因此，对医暴舆情的热度进行监测与分析，发现医暴舆情发展的关键介入时期，降低系列事件对社会产生的负面影响，则显得尤其重要。

由于上述原因，越来越多法学者开始关注舆情热度。如赵磊等[1]建立了基于BP神经网络的舆情热度仿真模型，杨长春等[2]尝试通过建立舆情敏感信息库并引入网络舆情关系指标来对突发事件进行热度分析与预测，兰月新等[3]基于灰色关联度方法，构建网络舆情热度模型与多维度logistic模型，对各个媒体平台舆情信息开展预测。然而需要指出的是，上述研究侧重于分析舆情热度本身的变化趋势，对于与舆情有高关联度的公众情感缺乏考虑。而隐马尔科夫模型作为解决通过已知状态推测未来状态一类问题的方法，符合本研究中舆情热度与公众情感二重随机的特征，进入了舆情热度的研究领域。目前已有学者做出有益的尝试。如何建民等[4]在《面向微博舆情演化分析的隐马尔科夫模型研究》一文中，选择网民特征、信息主题和信息内容完整度三维指标，构建了面向微博舆情演化分析的隐马尔科夫模型，揭示了微博舆情演化发展的一般规律。本研究在此基础上，采用HMM模型，针对突发医暴事件，在互联网上进行数据收集，尝试构建舆情热度与舆情情感相关的HMM模型，通过实证得到的状态转移矩阵与观测矩阵，深入剖析医暴舆情热度。通过选择医暴事件为主题进行实例分析，对医暴舆情热度变化进行追踪，并提出切实有效的措施，以此为相关舆情监管部门提供借鉴。

1 实证研究

1.1 隐马尔科夫模型

隐马尔科夫模型（HMM）是一个基于马尔科夫过程的随机模型，它包括一系列有穷状态集，以及与状态对应的观测序列，状态之间的转移是由状态转移概率矩阵来表示。由于实际观测到的是观测序列而不是状态本身，因此把从观测序列得到隐状态的过程叫作隐马尔科夫过程[5]。

隐马尔科夫模型由状态转移概率分布、观测概率分布以及初始概率分布决定。其形式化表示如下 ：

假设Q是所有序列的集合，F是所有可能的观测序列的集合。

Q= {q1,q2,…,qN},V= {v1,v2,…,vM}

上述表中，N是状态序列的规模，M是观测序列的规模。

I为状态序列，O对应的观测序列，长度为T。

I= (i1,i2,…,iT),O= (i1,o2,…,oT)

A是状态转移概率矩阵，如下所示：

A= [aij]N×N

其中，

aij=P(it+1=qj|it=qt),i=1,2,…,N;j=1,2,…,N

是在时刻t处于状态qi的条件下，在时刻t+1转移到状态qj的概率。

B是观测概率矩阵：

B= [bj(k)]N×M

其中，

bj(k)=P(ot=vk|it=qj),k=1,2,…,M;j=1,2,…,N

是在时刻t处于状态qj的条件下，生成观测vk的概率。

π是初始状态概率向量：

π=(πi)

其中，

πi=P(il=qi),i=1,2,…,N

是时刻t=1处于状态qi的概率。

隐马尔科夫模型有观测概率矩阵B、状态转移概率矩阵A和初始状态概率向量π决定。A和π决定状态序列，B决定观测序列。因此隐马尔科夫模型λ可以用三元组符号形式化表示，如下式所示：

λ=(A,B,π)

A、B、π是隐马尔可夫模型的三要素。

1.2 指标选取及数据来源

突发医暴事件舆情中，民众的情感强度变化与事件发展的热度都有着紧密的联系。热度作为舆情事态发展最直观的表现，是医暴舆情HMM模型的观测状态，并以发帖数、评论数、转发数、点赞数等指标维度描述医暴舆情热度。而舆情热度往往受隐藏在背后的民众情感所驱使，故舆情情感为HMM模型的隐状态，并选取情感强度指标进行界定。

哈尔滨伤医事件的实验数据源于新浪微博，统计时间段为8月15日12：00到8月17日23：00。以时段累加分组收集事件直接相关微博的评论数、转发数、点赞数和评论文本，随后通过熵权法计算出每时段热度值。使用Hownet知网情感词典方法对评论文本的情感值进行打分，结果仍按照小时累加统计，最终得到各时段内的情感强度值。

1.3 哈尔滨医暴舆情结果分析

定义传播标准值增量为后一时段标准值与本时段标准值之差。根据数值大小，将标准值增量样本集合划分为4个状态空间,即S1=[-0.4024，-0.0503],S2=[-0.0503,0]，S3=[0,0，02]，S4=[0.02，0.9143]， 对应舆情热度的快速上升状态，缓慢上升状态，缓慢下降状态，快速下降状态。以4个状态空间作为模型的隐状态空间。定义A矩阵为状态转移矩阵，B矩阵为输出概率矩阵。

经处理后部分数据如表1。

通过以上数据训练HMM算法，得到A与B。

分析得出，当医疗暴力事件舆情热度处于初始形成阶段时，舆情关注度增度处于S4区间的概率显著高于其他状态，这表示医暴事件正在被快速传播，公众接受了大量驳杂的相关信息，其情感强度急速上升，此时虚假消息极易被大范围传播以致误导公众，需要引起有关部门的注意。

当最高概率区间演变至S3状态时，舆情处于平稳发展阶段，此阶段医暴事件已经引起相当一部分公众的关注，同时信息逐渐变得全面客观，网络上形成了多种看法并趋于平稳，医暴舆情具有了一定规模并走向高潮。公众的情感强度也达到顶峰，并开始产生巨大的影响力。而此阶段内权威信息的披露能起到较好的舆论接受度，有利于舆论的引导与事件的解决。

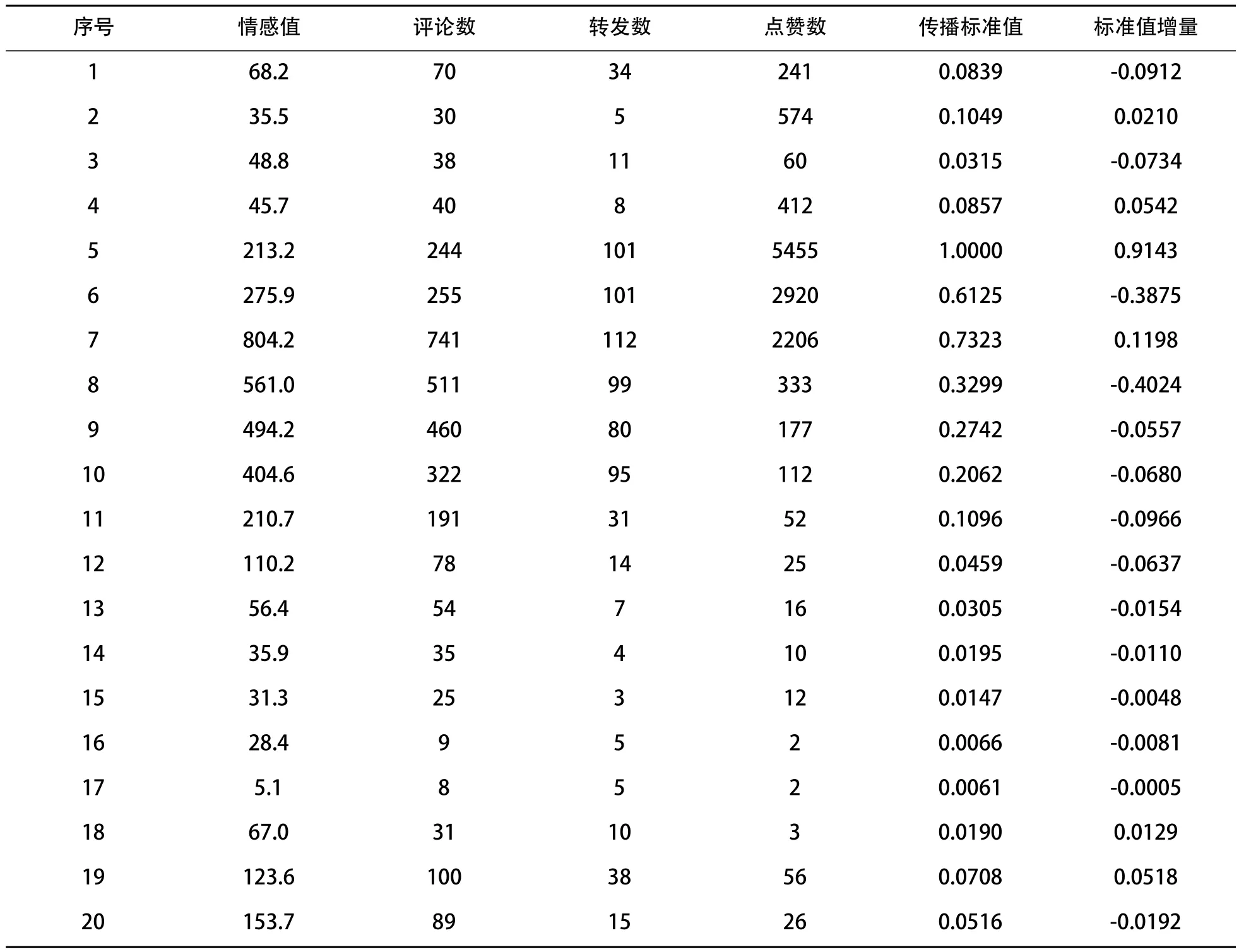
表1 经处理后的部分数据

在随后而来的波动阶段内，医暴舆情关注度增度在S2与S3之间反复变化，同时伴随着低概率的S1与S4状态，这代表着事件受众群体发生稳定更迭，同时也是舆情转入消亡阶段的重要标志。在这一阶段，公众被其他事件影响，对此事件的情感强度开始下降，伴随而来的舆论对事件的影响力同样减小。这一阶段内，除非事件发生重大转折，否则舆论观点将持续稳定，直至消失，官方说明解释不易起到理想效果。

2 结论

本研究通过对突发医患暴力事件的互联网舆情数据进行追踪处理，构建了相关的隐马尔科夫模型，来探讨医暴事件舆情热度的变化规律。

医患纠纷问题一直为社会热点问题，医患暴力事件也从未淡出过人们视野。然而在现阶段相关问题事件无法得到彻底解决的情况下，如何检测并分析其舆情热度变化，建立历史数据库或训练较高精度的模型，乃至对单个和多个医患暴力事件的舆情热度进行准确预测，将会是未来互联网舆情领域重点关注的问题。并希望在舆情的不同阶段对舆情采取相应的措施，以达到通过舆情促进事件解决的目的。

纵观整个医暴事件舆情热度发展，不难发现，在其初始形成阶段与平稳发展阶段，舆情发展极不稳定，此时官方的介入与信息披露都将起到良好的导向效果与稳定作用，利于减少虚假信息的大氛围传播达到稳定管控舆情的作用，且效果持续时间较长。在随后的波动阶段与消亡阶段，医暴事件的影响往往开始缩小至一小部分人群并淡出主流视野，此时再对其进行引导管控则效果不大。

而对应到具体事件的发展，在医暴事件舆情的初始形成阶段，公众对事件的来龙去脉并不清楚，因此容易被错误的信息引导，产生“沉锚效应”，使得事件最初的走向变得不可控。此时应该针对错误言论进行公开解释或清理，还原事态真实情况，促进公众对事件正确的了解。而在医暴舆情的平稳发展阶段，医暴事件备受社会瞩目，成为热点事件，这时接受不同的或不完整的信息的公众在新媒体平台上产生海量观点与评论，且极易形成激烈冲突，乃至形成舆论暴力，将当事人或管理者推向舆论的风口浪尖。这不仅对当事人造成难以治愈的心灵伤害，而且使得医患关系进一步恶化，社会矛盾持续加深。对此，应倡导规范的公众言行，做出有意识的引导，防止社会舆论对于事件的看法走向极端。同时由于此时信息传播极为迅速，网络舆情易出现不可控状态，必须防止水军恶意传播虚假消息，防范舆论暴力。在最后的医暴舆情的消亡阶段，随着事情真相的大范围传播，公众对问题的认识基本不会改变，舆情趋于稳定。此时，应以事件的解决方案来回应公众，并采纳合理建议，为医患纠纷提出正确恰当的解决方式，逐渐修复医患关系，重建社会信任。良好结果不仅为日后的医患纠纷提供借鉴，更可缓和医患关系，重建社会信任链条。

[1]赵磊,王松.基于BP神经网络的舆情热度趋势仿真模型研究[J].情报学报，2016,35(9)：989-999.

[2]杨长春,袁敏.基于交互关系的突发事件热度预测研究 [J].现代情报，2017,37(3)：40-45.

[3]兰月新,刘冰月,张鹏等.面向大数据的网络舆情热度动态预测模型研究[A].情报杂志，2017,36（6）：105-110.

[4]何建民,李雪.面向微博舆情演化分析的隐马尔科夫模型研究[A].情报科学，2016,34（4）：7-11.

[5]宰祥顺.基于隐马尔可夫模型的推荐算法研究[D].黑龙江：哈尔滨商业大学，2017.