“数学遇见春天”
2018-06-30高丽君张宏伟
高丽君 张宏伟


[摘 要]将集趣味性、广泛性、神秘性于一体的斐波那契数列,以儿童化的方式置于小学数学课堂中让学生进行探究,是对全景式数学教育“跨领域建设融合性数学项目课程”理念和“全方位、全时空、全身心、全自主”学习主张的践行与落实。它融合了数学、科学、生物等多门学科知识,通过课堂教学和游学实践相结合的方式,最终以项目课程的模式呈现,达成复习知识、提升能力、启迪智慧、激发兴趣、拓展数学视野、丰富认识、培养综合素养的全景式数学教育目的。
[关键词]全景式数学教育;学科整合;斐波那契数列;浪漫
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2018)15-0001-003
2017年春,和朋友小聚茶室,边品春芽,边倚窗赏绿柳春花。不知怎的,几个朋友忽地就聊到了斐波那契数列(又称黄金分割数列,指的是0、1、1、2、3、5、8、13、21、34……这样一个数列)。斐波那契数列听起来高深莫测,实则为一组符合一定规律的数字。也许是师傅那句话“数学老师要时刻用数学的眼睛看待一切,时刻思量如何整合出更具孩子气、更饱满有趣的综合课程”引发了我的思考:“这不正是学生认识规律、认识自然、复习100以内加减法最好的课程资源吗?”于是,“数学遇见春天”微项目课程如春花般绽放开来。在这个万物复苏的季节,我和学生走近自然,遇见了春天,遇见了科学,遇见了数学……给他们的童年留下了一份美丽、神奇、难忘的记忆。
游学前——浪漫感知斐波那契数列
斐波那契数列在人类发展史上有着举足轻重的作用,它因与自然界有诸多的联系而被称作为神奇数列。这种具有递推特征的数列在植物界中的体现最为明显,如自然界中大部分花的花瓣数量就是斐波那契数。因此,“数学遇见春天”的微项目课程就从数花瓣开始,让一年级学生发现大自然中很多事物都是按照一定的规律生长的,从中感受到大自然和数学的神奇,激发他们对数学的热爱之情。
正值春暖花开,级部安排去世界花卉大观园进行游学活动。根据一年级学生的心理特点和认知规律,游学前一天的晨诵时间,我带领学生数不同花的花瓣。低学段学生看到美好的事物都很兴奋,有很高的兴致数数。教学过程如下:
师:现在各种花都开了,今天看看哪位“小蝌蚪”认识花的种类多。(话音刚落,学生眼里充满期待)谁见过一片花瓣的花?(学生一时想不起来,于是师出示马蹄莲的图片,学生惊叹世界上还有这么美丽的花)
师:你们猜,我下面会让你们说一说几片花瓣的花?
生:1片花瓣的花,2片花瓣的花,4片花瓣的花……(学生根据自己的经验争论不休)
师:你们的思考都很棒!接下来,我的问题是你能再说出一种一片花瓣的花吗?(在学生的期待中,师顺势出示花烛和2片花瓣的虎刺梅的图片)
师:仅仅看数字1、1、2,能猜测这些花可能符合什么規律吗?
生1:1+1=2,还不能确定。
(师继续出示3片花瓣的铁兰)
生2:老师,我猜你下一步会出示5片花瓣的花。
师:为什么会这么认为?
生2:因为这几个数字是有规律的,如1+1=2、1+2=3,把相邻的两个数加起来就是下一个数字,所以我猜测你下一步会出示花瓣数量是2+3=5(片)的花。
师:数学学习需要进行猜想,但猜想后必须要验证,验证之后才能见分晓。(师点击PPT,画面中出现三种5片花瓣的花,分别是洋紫荆、黄蝉、蝴蝶兰,教室里顿时沸腾了!学生一方面惊叹于花的美丽,另一方面猜想正确的喜悦大大鼓舞了他们)
生3:下面要出示8片花瓣的花,因为3+5=8。
(师出示8片花瓣的格桑花)
……
学生在这个过程中已经找到了规律,尽管有些隐晦,不似间隔相同数字那样清晰,但他们的思维已经被激活。紧接着,我出示13片花瓣的雏菊和21片花瓣的紫菀给学生验证,学生热情不减。然后我不再出示花的图片,而是让学生运用规律计算出将要出现的数字,依次为1、1、2、3、5、8、13、21、34、55、89。这样,我在轻松愉悦的氛围里带领学生复习100以内的加法,学生兴致勃勃。
计算至此,我问:“算到89,还能继续吗?”一学生说:“后面还能不停地写出很多个数,写到我八十岁都写不完!”这个学生的回答得到了大家的一致认同,但大家也被他“写到八十岁都写不完”的话逗乐了。提出这个问题,我的目的是让学生尝试理解数列的无穷性。在这个过程中,我发现一年级学生虽然不能用精准的数学语言描述数列的无穷性,但已经能够在找规律过程中体会并理解数列的无穷性。
为了让学生知道具有一定规律的一组数字叫数列,我问学生:“如果很多数字按照规律排成一列,应该叫什么呢?”学生猜测:“数字列。”我听后喜出望外,引导学生改进名字:“如果去掉一个不太重要的字的话,你会去掉哪个字?”一生思考后回答:“我觉得‘字容易让人想起汉字,跟数学关系不大,可以去掉。”……虽然一年级学生的认知水平有限,但不影响他们从字面上进行简单、合理的判断,而且学生的发现和创造也遵循了人类最原始的思维路径。我进一步告诉学生:“这一列数字是由一个叫斐波那契的人发现的,所以它叫斐波那契数列。”……要知道,斐波那契数列的第一次正式出现是在人教版高中数学必修五学习数列概念后的课后阅读部分。在这个发现规律的过程中,学生理解“1、1、2、3、5、8、13、21、34、55、89”这一列数字不是随便的数字,而是具有一定的规律,蕴含了与数列相关的函数思想。这样的认知过程与学生已有的知识经验产生“化学反应”,激起学生的情感共鸣,引发他们对数学的热爱以及对自然界的惊叹,发现数学之美。
游学中——实践探索斐波那契数列
1.户外渗透数学思想
第二天去世界花卉大观园进行游学活动,我专门设计了游学单(如下图),以期培养学生记录、发现、分析等方面的能力。同时,让课堂上学习的内容再回归到大自然中,学以致用,使学生进一步感受到数学与生活的密切联系,发现自然的“密码”(万物皆数学),体验到数学的应用价值。
学生需要记录的内容包括花的名称、颜色、花香程度、花瓣数量、花蕊数量等,需要解决的问题包括比较问题、相差问题、分类问题等。这样不着痕迹地把数数、统计、比较、加减法运算等内容融入游学活动中,既巩固了本阶段学生所学的知识,又提高了学生学习数学的兴趣。
2.延伸科学知识
斐波那契数列在自然界中的体现远不止花瓣数量,我抓住游学活动这个契机,引导学生通过亲身体验继续发现、探究,开拓知识视野,使他们体会到数学的神奇和无处不在。
游学活动时,我结合真实生长的树进行现场授课:“一个新发的树枝在第一阶段主要吸收养分,不分叉,树枝数量为1;第二阶段继续汲取营养生长,为分叉做好准备,但树枝数量还是1;第三阶段,生长时机成熟,分叉,树枝数量是2;第四阶段,老树枝分叉,上一阶段新发的树枝继续生长不分叉,树枝数量为3;依次类推,树枝数量依次为1、1、2、3、5、8、13……符合斐波那契数列的规律。”
此外,我还让学生找到松果种子,数它的螺旋排列,发现顺时针数是8条,逆时针数是13条,为斐波那契数;菜花表面排列的螺旋线,顺时针数是5条,逆时针数是8条,为斐波那契数;还有向日葵的螺旋线也是斐波那契数……
游學归来,我又在课间补充了经典的“兔子问题”:“1对小兔子→1对大兔子→1对大兔子+1对小兔子(共2对兔子)→2对大兔子+1对小兔子(共3对兔子)……”这个过程以动态PPT的形式展示,学生在“数数→猜测→数数”的过程中体会到数学的有趣。令我欣喜的是,故事还没讲完,就有学生联想到树枝分叉的情境,解释说“小兔子需要生长一个阶段之后再生小兔子”。学生把“树枝分叉”和“兔生兔”两个不同的例子联系起来,说明他们既理解了两者之间的共性,又体会到万物生长的相似性以及数学解题模型之间的互通互联。
游学后——初步精致化斐波那契数列
1.课堂的数学化
游学归来,学生依旧沉浸在数花瓣的氛围之中,我计划用花瓣数量继续进行单元复习。课堂上,我新建了一个空白的Excel表格,首先做了表头,有“花名”“花瓣数量”两项,然后在“花名”下面依次填入上一阶段认识的花。没等我输入完,大部分学生都猜到要填入的花瓣数量。接着,我故弄玄虚,说要做一件大事,学生都静静地望着我。我熟练地“插入”柱状图,通过刚刚完成的数据表格,形成如下的柱状图。
师:这叫柱状图(全景式数学教育之“浪漫”认识),即用小柱子的长度表示数量。现在大家猜一猜,为什么有高矮不同的柱子呢?
[为什么要引入柱状图?在进行比较的时候,柱状图具有较强的直观性,能帮助学生建立更具体、更形象的认知系统。]
生1:高矮不同的柱子跟花瓣的数量有关系,也就是说花瓣的数量越多,柱子越高,如马蹄莲和紫菀的柱子高度就相差很多。
生2:每个柱子的头上都顶着花瓣数量呢!
师:从这幅图中,你可以提出什么数学问题?(一共有八种花瓣的数据,给学生提供了充足的素材去提出数学问题)
生3:格桑花和雏菊的花瓣一共有多少片?这是一个用加法解决的问题。
(其他学生的思维被激活了,连续提出几个用加法解决的问题,包括三个数相加、四个数相加、五个数相加等一系列的连加问题)
师:刚才提出来的问题都是用加法解决的问题,根据这幅柱状图,还能不能提出别的类型的问题呢?
生4:紫菀比蝴蝶兰多多少片花瓣?这是一个用减法解决的问题。
师:请大家思考,这个问题除了可以这样问外,还可以怎样问呢?
生5:还可以问“蝴蝶兰比紫菀少多少片花瓣”“紫菀和蝴蝶兰相差多少片花瓣”,这三种问法都可以用同一个算式21-5=16解答。
……
复习课上,学生这样的联想能力让我很兴奋。紧接着,我又让学生分别用这三种问法提问,以巩固学生对这一知识点的掌握。就这样,在轻松、愉悦的氛围中,学生以同一个数学算式用三种方法提数学问题的方式“攻克”了本课的教学难点,且“提出数学问题并解答”本身已经高于“会做题”的认知水平。
师:由“……比……多多少”和“……比……少多少”这两类问题,你还可以想到其他的问题吗?
生6:看着这幅图中高高低低的柱子,我想起第一单元“学说话”时“多得多”“多一些”“少得多”“少一些”等问题。如紫菀的花瓣数量比马蹄莲多得多,蝴蝶兰的花瓣数量比铁兰多一些,花烛的花瓣数量比紫菀少得多,刺虎梅的花瓣数量比铁兰少一些。
……
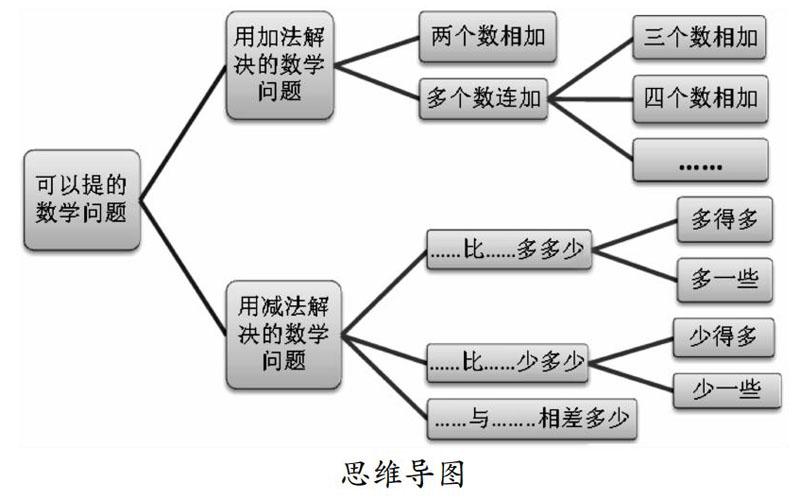
然后我让学生以小组合作的方式,用“多得多”“多一些”“少得多”“少一些”四个词给同桌说四句话,以巩固学生对这一内容的学习。至此,提问环节结束,整个过程,我以思维导图(如下)的形式记录下学生的所有回答并分类。这样教学,使学生系统、全面地复习并巩固了100以内各种类型加法、减法解决问题的题目,以及相应进位加法、退位减法的计算问题,这些问题包含甚至超越了一年级解决问题的所有类型。同时,我在教学中渗透了找规律、统计等知识,引导学生从整体的角度沟通了知识之间的内在联系。
2.课后的拓展与延伸
基于课上整体的教学内容,我布置了两项趣味性课后作业,以巩固学生课堂所学的知识。
家庭作业(1):运用斐波那契数列,破解老师家的14位wifi密码。
第二天课堂上,学生都兴奋地表示已经破解我家wifi的密码——11235813213455,还有的学生表示自己家的wifi密码已经改为斐波那契数列,原因是家长觉得这一列数字很有意思,而且可以作为孩子学习的一个纪念。
同样是加法练习,变换形式会给学生带来不一样的情感体验,使他们体会到加法并不仅仅可以用来解决“一共有多少”的问题,还有很多有意思的应用。这个做作业的过程,拓展了学生的数学认知范畴,并在学生的脑海中埋下数学有用、数学好玩的种子。
家庭作业(2):用“画正法”统计家里桌子、碗、筷子的数量,并比较谁的数量多、谁的数量少,最后列式计算相差多少。
这一作业与实际生活紧密联系,看似简单,只是数数桌子、碗、筷子的数量,实则融合了统计、比较、减法等知识,旨在提高学生解决实际问题的能力。
这个春天,我带领学生在数学的世界里“花式数数”——数花瓣、数树枝、数螺旋线、数餐具……实现了由“实物→图形→数字”的逐步抽象过程,引导学生复习了100以内的加减法,使学生不仅学会发现规律、提出数学问题,还认识了奇妙的自然界。这种趣味性的学习,使学生在知识学习和情趣培养方面都有很大的发展,可谓“居室内,文理兼容,内外兼修,阅大千世界”。在这个过程中,学生发现数学那么有用、那么神奇、那么好玩、那么有意思!
我和我的“小蝌蚪们”永远不会忘记,一年级我们循着季节时令,一起在美丽的大自然里吻醒了烂漫的春花,吻醒了冰冷的数学,吻醒了我们内心深处等待开启的自己……
(责编 杜 华)
