等比数列(第一课时)教学设计

山东省滨州市沾化区第二中学 张明贵

一、教学目标

知识目标：通过教学使学生理解等比数列的概念，推导并掌握通项公式。

能力目标：使学生进一步体会类比、归纳思想，培养学生的观察、概括能力。

情感目标：培养学生勤于思考，实事求是的精神及严谨的科学态度。

二、教学重点和难点

重点：等比数列的定义，通项公式的猜想过程、理解。

难点：等比数列的通项公式的应用。

三、教学用具

多媒体

四、教学过程

（一）创设情境

情景引入生活中实际的例子．

1.细胞分裂问题，可以记作数列：1,2,4,8,…． ①

3.计算机病毒感染可以记作数列 ：1,20,202,203,204…

观察三组数列的共同特征．从第2项起, 每一项与前一项的比都等于同一常数.

（二）讲解新课

1.等比数列的定义

一般地，如果一个数列从第二项起，每一项与它前一项之比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做这个数列的公比，用q表示,(q ≠0)．

（2）对定义的认识

①等比数列的首项不为0； ②等比数列的每一项都不为0;

2.等比数列的通项公式

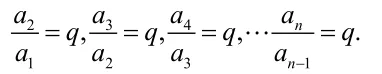
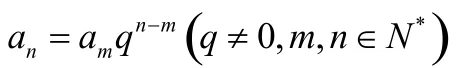
3.等比中项

若a, G, b 成等比数列,那么G叫做a与b的等比中项.G2=ab

4.等比数列与指数函数的关系

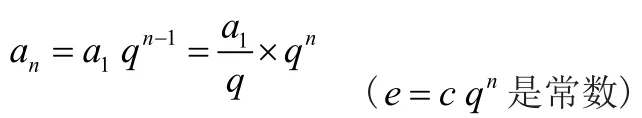
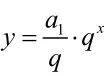
n 的离散的点.

5.等比数列的判断方法

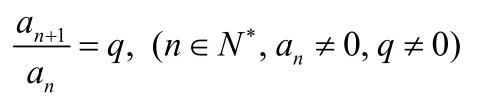
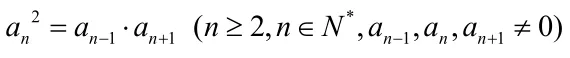
6.例题讲解

例1 一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项．

解 设这个等比数列的第1项是a1，公比是q，那么

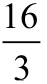
例2 已知{a },{b}是项数相同的等比数列，求证

n n{an·bn}是等比数列.

证: 设{an}的公比为p,{bn}的公比为q,

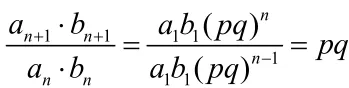
∴{ an·bn}是公比为pq的等比数列.

7.当堂演练

在等比数列{an}中：

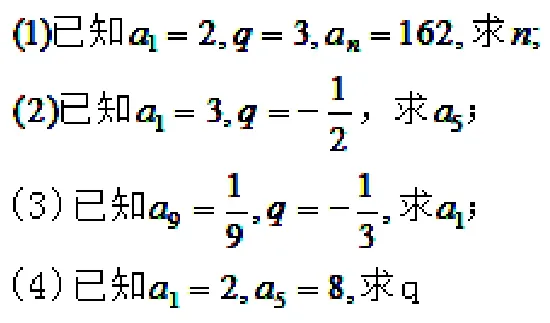
8.课堂小结

①等比数列的定义，等比数列的通项公式；

②注意在研究内容与方法上要与等差数列相类比；

③用方程的思想认识通项公式，并加以应用．

9.课后作业

课本P53习题2.4 A组第1题，B组第1题.