高效数学课堂模式探讨

山西省长治市武乡县武乡中学校 魏翠萍

“1+1”学案模式课：一节自主课 + 一节展示课。

一、“1+1”学案编写

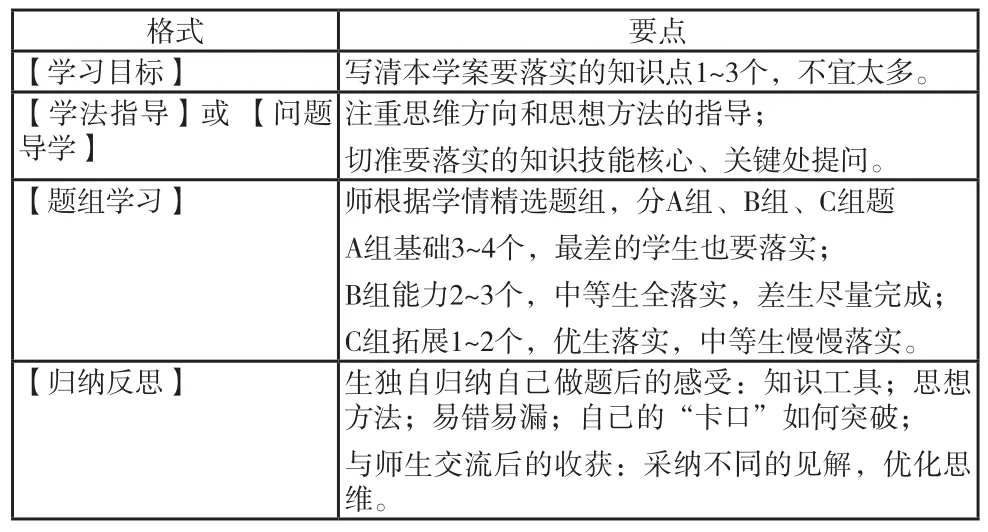
格式 要点【学习目标】 写清本学案要落实的知识点1～3个，不宜太多。【学法指导】或 【问题导学】注重思维方向和思想方法的指导；切准要落实的知识技能核心、关键处提问。【题组学习】 师根据学情精选题组，分A组、B组、C组题A组基础3～4个，最差的学生也要落实；B组能力2～3个，中等生全落实，差生尽量完成；C组拓展1～2个，优生落实，中等生慢慢落实。【归纳反思】 生独自归纳自己做题后的感受：知识工具；思想方法；易错易漏；自己的“卡口”如何突破；与师生交流后的收获：采纳不同的见解，优化思维。

编学案要根据目标定内容，根据内容定题量，试题要有代表性，少而精，确保“1+1”能完成。【问题导学】与【学法指导】有时可合并，二者要兼顾。

二、自主课模式

生独立完成学案（约30分钟）

生活动：安静地、独立地思考完成学案，相当于一个限时训练。

师活动：师来回细致地观察学生答题情况，一方面督促生答题，另一方面了解学情。看速度、看准确度、看生思维优劣、看每题对生难易情况，看出共性问题与个性问题等。师要根据学情，看是否需要调整教学设计。

师点拨（约7分钟）

师根据看到的情况，个别点拨（其他学生仍在独立完成）：

1.基础知识工具（如概念、公式、定理）有误的学生；

2.大部分同学会而该生不会的；

3.有好的思维方向而难以进一步突破的学生。

通过师点拨，燃起学习中出现不同类型困难的学生的学习激情和坚持不懈的意志品质。

生生交流、师生交流（约7分钟）

1.小组内对答案，交换思维；组长负责本组成员“有人会，本组人就要会”；

2.异组交流，组长间的交流。

交流一题多解，不会的题突破口，三个“臭皮匠”看能否顶一个“诸葛亮”将不会的题“凑”出来。

3.师适时地、平等地参与进去，顺着学生的思维方向讨论，使学生的思维得以迸发出来。

4.师布置下节课班级交流的内容、位置与展示学生（约1分钟）

师整合学情，把能体现本学案思想方法的或一题多解的或思维有“卡口”的定为展示内容；

遵循自愿展示的原则，确定展示人；

重点内容，重点位置展示。

三、展示课模式

1.师培训学生

师将要展示的题摘录出来后，本着生自愿的原则，让生自觉、自愿地承担展示任务。课下，让展示的学生先给师讲一遍，行的通过，否则，师顺着生的思维适当点拨；当生说不清时，师要耐心地引导生使其思维得以优化，让他再讲，直到师生达成共识为止。注意：展示的学生必须讲究效率，但师切记不能主宰生的思维。这一环节师可以一拨一拨地培养学生“敢于发言”到“善于发言”。积极上进的学生都会踊跃参加的。

2.展什么、怎么展

展什么：展重点、展难点 怎么展：重思维、重过程全会的，不展 师一定要把好关，确保人人会

展重点内容中，一部分同学还不会的课前到指定位置写好步骤或适当写步骤，重点突破时边讲边完善，最终形成完整的答案展难点，知识点复合多，无思维方向的课前几乎不写，展示时先分析题，带领同学们从分析中找到思维方向，理清思维的几个层次，然后一层一层的写好步骤，从而突破难点，提升大家的思维品质

每位学生展示完成后，都要说“大家还有别的见解吗？（或还有疑问吗？）有请下一位”，这时其他同学听后，有的大有收获，有的见解不同会形成一种质疑，讲错时同学们还会及时纠正等等，一种充满生机、充满思维碰撞的课堂自然形成！

3.师作用

师生首先平等地参与课堂教学活动，但师针对课堂中学生的表现，有必要时也应及时点拨、完善、拓展，尤其本节错误之处，最好及时纠正。其次，师必须发挥好课堂的主导作用，学生难以形成的知识体系或思想方法，教师必须引导学生提升他们的数学素养。

4.归纳反思，重建知识体系

针对老师学案中设计的【学法指导】或【问题导学】，切中问题的实质来归纳、总结，从知识点到思想方法言简意赅。

四、实践后感受

编“1+1”学案对教师要求很高。先要研究新课标和高考，从做大量的高考题中找准考向，定下教学目标，结合学情，精选题组。这需要老师付出大量的时间和精力，才能编出适合自己所教学生的好学案。

自主课上老师一点也不轻松，师不能坐着而要不停的“看”，并要“看”出学情，整合信息，定出展示目标；同时，这也是一个与学生思维碰撞、心心交流的过程，师的真诚会激发出学生潜在的正能量。

展示课要想成功，而不浪费大部分学生的时间，教师课前必须培养发言的学生，让他们充满自信地表达自己的想法，别人听后才能有收获，同时该生的综合素质也会有所提高。

不论传统课堂还是课改课堂，学生课堂收获的多少是决定课堂是否高效的关键。要想真正实现高效课堂，既需要教师科学地管理学生，充分调动学生的学习积极性；也需要学生不懈的努力，取长补短，不断地重建自己的知识体系，真正将课堂知识内化为自我的知识技能。

附学案：

【学习目标】

1.用活导数的几何意义；

2.准确理解“用导函数f′(x)的正负来研究原函数f(x)的增减”，并会对f′(x)灵活变形。

【学法指导】

1.用方程（组）思想思考求一个或几个量的值；

2.积累求导后的变形方向；

3.用心体会“卡口”处自己到底缺少什么？

【题组学习】

（A组1）（1）设曲线处的切线方程，求a,b的值；

（B组）（2）求f(x)在[0 ,+∞)内的最小值.

（A组2、3）（1）求f(x)的解析式及单调区间；

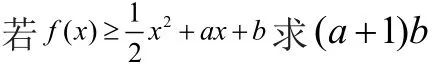
【归纳反思】写在《学习报告本》上。