带有未知死区非线性系统的自适应控制方案

李雷雷

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

0 引言

近年来，自适应模糊跟踪控制受到了学者们的广泛关注。在实际应用过程中，模糊控制经常被用来解决系统的控制效果不佳以及系统不稳定的不利干扰问题[1-2]。因此，在控制器的设计过程中构造一个系统约束是至关重要的。在文献[3]中，一个基于观测器的非线性系统的自适应模糊控制方法被提出。在文献[4]中，利用自适应模糊控制，结合帕德近似和自适应反步法，提出了一种新颖的控制方法来处理输入延迟的问题。不同于上面的结果，对于系统状态和非线性死区输入，在文献[5]提出了一个多变量非线性的自适应模糊控制方案。

未知死区经常出现在实际的非线性系统中，很容易导致系统的不稳定，从而造成较大的误差。因此，关于非线性系统的稳定性分析和控制系统的设计成为一个值得研究和探索的问题。死区在许多实际非线性系统中会严重影响系统性能。例如，流体系统、仪器领域、无线波通信、伺服电机[6-8]，这些系统都含有死区输入。在处理上述应用程序时，存在死区会造成许多困难，这一问题在过去十年中得到了广泛的研究。控制死区比较有用的方法是构造一个自适应死区逆[9]。因此，文献[10]采用非最小相位线性动力学，对已知的未知死区输出死区进行逆补偿。文献[11]利用自适应死区逆的死区补偿输出，为线性离散系统设计了一个离散自适应控制方法。文献[12]通过引入光滑的逆函数的死区，设计了一种自适应输出控制方法。其他方法如采用神经网络，文献[13]设计了一个自适应控制器，来解决在工业过程控制系统死区的各种问题。在文献[14]中，针对严格反馈非线性系统与完全未知的虚拟控制未知死区系数，作者给出了一种鲁棒自适应神经控制设计方法。

许多研究基于线性系统死区模型，然而，在实际系统中非线性系统死区的干扰也是很常见的问题。针对这个问题，笔者对一类非线性系统死区输入建立了一个基于补偿器的自适应模糊控制方案。对于线性化的非线性死区模型，本研究克服了非线性死区输入对系统稳定的影响，证明了闭环系统的稳定性，保证了闭环系统所有信号半全局一致有界，并且系统的跟踪误差收敛到一个原点小邻域。本研究的创新点在于考虑了更一般的未知死区系统形式，通过构造滤波器，定义误差补偿信号，系统死区的干扰被解决。

1 问题分析

考虑下面的非线性随机纯反馈系统

(1)

u∈R表示系统死区输入，它的表达式为

(2)

其中，v表示死区输入信号，mr和ml分别表示死区的右斜率和左斜率，br和bl表示非线性输入的间断点。方案的目标是构造一个控制律来调节系统输出x1跟踪到给定信号xd。为了完成反步法的设计，引入下面的定理和假设。

定义1[15]对于任意函数V(x，t)∈C2，1和非线性控制系统方程(1)，定义微分算子

(3)

其中，Tr(A)表示A的迹。

定义2 对于全集Ω∈Rn和初始状态x0=x(t0)，如果存在常数ε>0和一个时间常数T=T(ε，x0)，对所有的t>t0+T，满足E(|x(t)|p)<ε，则称非线性控制系统(1)的轨迹{x(t)，t≥0}半全局一致有界，其中E(|x(t)|p)表示|x(t)|p的期望。

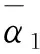
(4)

则对于任一x0∈Rn，有

(5)

假设1 参数mr和ml是未知的正常数。存在正常数bm和bM，使得0≤bm≤min{ml，mr}≤max{ml，mr}≤bM。

为方便起见，根据文献[11]，死区(2)式的输出能够被表示成下列形式

u=mϑ+d，

(6)

根据假设1，有|d|≤d*，其中d*=bMmax{|br|，|bl|}是一个正常数。

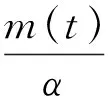
(7)

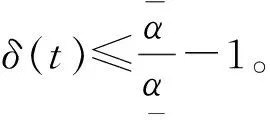
把(7)式代入(6)式，可以得到

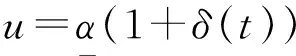
(8)

引理2[16](杨氏不等式) 对∀(x，y)∈R2，有

(9)

其中，ε>0，p>1，q>1，并且(p-1)(q-1)=1。

在反步法设计过程中，将用模糊逻辑近似系统中未知非线性函数。模糊逻辑系统函数被描述为[16]

y(x)=WTS(x)，

(10)

其中，x∈Ω⊂Rq表示状态的输入矢量，q是模糊逻辑系统的输入维度；W=[w1，w2，…，wl]T∈Rl权向量，l>1表示节点数；φ(x)=[φ1(x)，φ2(x)，…，φl(x)]T，表示基函数向量，φi(x)是高斯函数，它的形式为

(11)

其中，μi=[μi1，μi2，…μiq]T(i=1，…，l)，表示邻域中心；η是高斯函数的广度。模糊逻辑系统函数(10)能够逼近紧集Ω⊂Rq上的任意连续函数

f(x)=W*TS(x)+γ(x)，∀x∈Ω∈Rq，

(12)

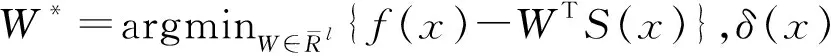
设计命令滤波的形式如下：

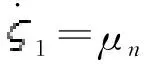
(13)

(14)

2 自适应控制方案

将基于反步法和模糊逻辑系统近似，对系统(1)给出一个自适应模糊控制方案。反步法需要n步，在设计过程中，构造虚拟控制信号αi(i=2，…，n-1)，

(15)

(16)

定义误差补偿信号ζi(i=2，…，n-1)，形式如下：

(17)

gi(xi+1，c-αi)，

(18)

(19)

其中，ci>0，ζ(0)=0，‖ζi‖是有界的，且满足

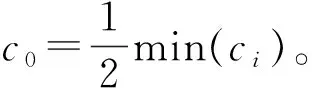
在反步法的每一步中，将用到下列坐标变换

z1=x1-xd，zi=xi-xi，c，i=2，…，n，

(20)

其中xd是给定的参考信号，xi，c表示命令滤波输出。定义补偿跟踪误差信号vi=zi-ζi。

第1步：考虑下列李雅普诺夫函数

(21)

则，由定义1得

(22)

由(9)式，可以得到

(23)

(24)

把(23)式和(24)式代入(22)式中，可得

(25)

再把定义的误差补偿信号(17)式代入(25)式得

(26)

通过设计的虚拟控制信号(15)式，(26)式可写成

(27)

(28)

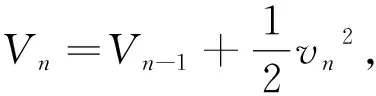
(29)

同样，由(9)式，得

(30)

(31)

把(30)式和(31)式代入(29)式得

(32)

把(19)式代入(32)式，可以得到

(33)

下面引入一个实际控制器：

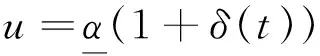
(34)

代入(33)式，有

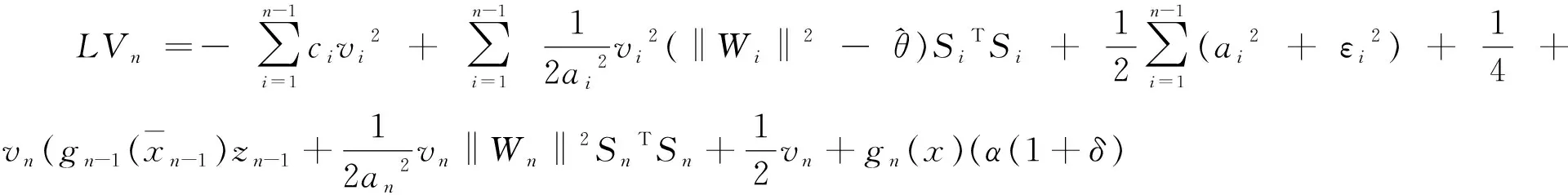
(35)

根据假设2，可以知道

(36)

将其代入(35)式，得

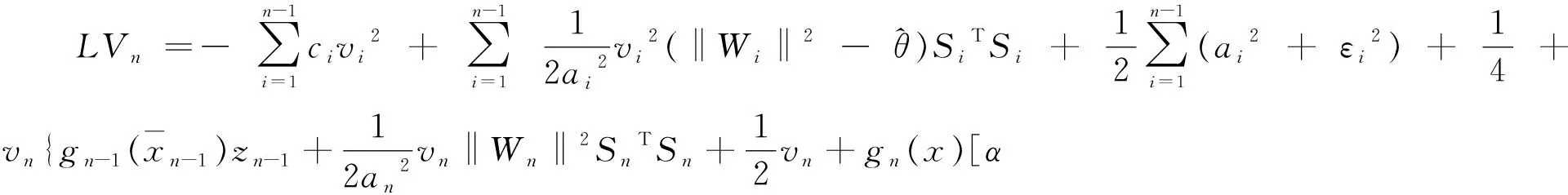
(37)

构造控制信号：

(38)

则(37)式可以被重写成

(39)

(40)

则可以构造自适应律为

(41)

其中Dm是一个已知正常数。

3 稳定性分析

把(41)式代入(40)式，得到

(42)

利用杨氏不等式(9)，得

(43)

将其代入(42)式，得

(44)

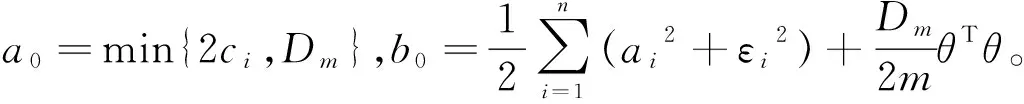
由引理1得

(45)

且

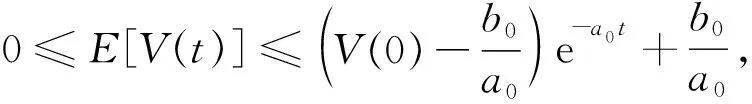
(46)

则

(47)

根据(46)式和(47)式，可得到

(48)

(49)

根据以上分析和讨论，得出下列定理：

定理1在假设1和假设2条件下，对于带有未知死区的非线性随机纯反馈控制系统(1)，基于模糊逻辑系统近似，利用反步技巧，通过设计适当的李雅普诺夫函数(21)，提出带有恰当虚拟控制信号(15)(16)，实际控制信号(38)，误差补偿信号(17)(18)(19)和自适应律(41)的控制方案，保证了非线性控制系统(1)的所有控制信号最终一致概率有界，跟踪误差收敛到紧集(49)。

4 结论

本研究针对一系列带有未知死区的严格反馈随机非线性系统，提出了一个自适应模糊控制方案。通过利用模糊逻辑系统近似地来识别系统中的未知函数，基于一个适当的李雅普诺夫函数，结合自适应反步法，构造控制信号和控制律，引入误差补偿信号，由此系统中的未知死区干扰被解决，保证了随机严格反馈控制系统的所有信号最终一致概率有界，跟踪误差最终收敛到一个相应的紧集。

参考文献：

[1] XIE X， YUE D， ZHANG H， et al. Control synthesis of discrete-time T-S fuzzy systems via a multi-instant homogeneous polynomial approach[J].IEEE Trans. Cybern，2016，46(3)：630-640.

[2] LI Y， TONG S C， LI T. Hybrid fuzzy adaptive output feedback control design for MIMO time-varying delays uncertain nonlinear systems[J].IEEE Trans. Fuzzy Syst.，2016，24(4)：841-853.

[3] LI T， LI Z， WANG D， et al. Output-feedback adaptive neural control for stochastic nonlinear time-varying delay systems with unknown control directions[J].IEEE Trans. Neur. Netw. Syst.，2015，26(6)：1188-1201.

[4] LI H， WANG L， DU H A. Boulkroune， Adaptive fuzzy back-stepping tracking control for strict-feedback systems with input delay[J].IEEE Trans. Fuzzy Syst.，2017，25(3)：642-652.

[5] BOULKROUNE A， MSAAD M， FARZA M. State and output feedback fuzzy variable structure controllers for multivariable nonlinear systems subject to input nonlinearities[J].Int. J. Adv. Manuf. Technol.，2014，71(1)：539-556.

[6] NURIEL P， WEINBERGER R， ROSENBAUM G， et al. Golding， timing and mechanism of late-pleistocene calcite vein formation across the Dead Sea Fault Zone[J].Northern Israel. J. Struct. Geol.，2012(36)：43-54.

[7] PENG J Z， DUBAY R. Identification and adaptive neural network control of a DC motor system with dead-zone characteristics[J].ISA Trans.，2011(50)：588-598.

[8] MISRA S， VAISH A. Reputation-based role assignment for role-based access control in wireless sensor networks[J].Comput. Commun，2011(34)：281-294.

[9] TAO G， KOKOTOVIC P V. Adaptive control of plants with unknown dead-zone[J].IEEE Trans. Autom. Control，1994，39(1)：59-68.

[10] TIAN M， TAO G. Adaptive output dead-zone compensation[J].IEEE Conference on Decision and Control，1997(2)：1157-1161.

[11] TAO G， KOKOTOVIC P V. Discrete-time adaptive control of systems with unknown dead-zone[J].Int. J. Control，1995，61(1)：1-17.

[12] ZHOU Q， WEN C， ZHANG Y. Adaptive output control of nonlinear systems with uncertain dead zone nonlinearity[J].IEEE Trans. Autom. Control，2006，51(3)：504-511.

[13] CUI X Z， SHIN K G. Design of an industrial process controller using neural networks[J].Proceedings of the American control conference，1991，49：508-513.

[14] GE S S， WANG J. Robustness adaptive neural control for a class of perturbed strict-feedback nonlinear systems[J].IEEE Trans. Neural Netw.，2003，13(6)：1409-1412.

[15] 李雷雷，刘西奎.任意转换下带有未知迟滞的随机非线性系统自适应跟踪控制方案[J].唐山学院学报，2017，30(3)：1-8.

[16] LI Y， ZHANG W H， LIU X K. Stability of Nonlinear Stochastic Discrete-Time Systems[J].Journal of applied mathematics，2013(2013)：1-9.