基于RBF网络最小参数学习法的机械手终端滑模控制

刘昕明，吕东东

（辽宁工程技术大学 电气工程与控制工程学院，葫芦岛125105）

滑模变结构控制以其对系统参数变化和外部扰动的鲁棒性而著称，线性滑模控制（LSMC）是系统到达滑模面后，跟踪误差渐进收敛至零[1]，并且可以通过选择滑动模态参数来调整渐进收敛的速度，但是无论如何调整，状态跟踪误差都不能在有限时间内收敛至零。为了解决无限时间收敛问题，采用终端滑模控制，通过在线性滑模面中引入非线性函数项和适当设计控制器，使得跟踪误差在有限时间内收敛到零，并且相对于线性滑模控制鲁棒性更强。由于TSMC自身也存在缺点会出现奇异问题[2-3]，为了避免奇异问题的出现，对终端滑模面进行了改进[4]。由于要设计的控制器依赖于机械手的精确数学模型，而机械手的某些项是不能确定的，可以采用RBF神经网络去逼近不确定项。RBF神经网络是一种非线性模型，具有收敛速度快、全局逼近能力强等优点，对于复杂不确定问题具有自适应能力和自学习能力，可以应用于非线性和不确定系统的控制器设计中[5]。为了简化自适应算法，增强实时控制的要求，用单个参数取代神经网络权值。把RBF神经网络算法和终端滑模算法结合起来控制两关节的机械手，并用Lyapunov定理证明稳定性，然后用Matlab/Simulink仿真实验。

1 机械手动力学模型

一个串行N关节机器人机械手的动力学模型可以用拉格朗日形式表示为[6]

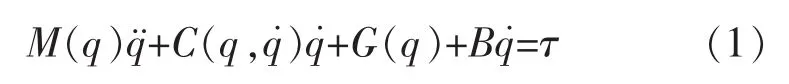
式中：q∈Rn是关节角位移量；∈Rn是关节速度矢量；τ∈Rn是施加的扭矩输入向量；M（q）∈Rn×n是非奇异的正定惯性力矩阵；C（q，）∈Rn是离心力和哥氏力项；G（q）∈Rn是重力力矩矢量；B=diag｛B1，B2，…，Bn｝是代表机器手的粘性摩擦系数的对角矩阵。

1.1 机械手的混合动力学模型

为了应用适当的控制算法，机器手动力学模型应该转换为每个关节点相对应执行器的等效动力学模型[7-8]。机械臂的每个关节是由直流伺服电机驱动的，在电机轴上机械手驱动器动力学数学模型可以描述为

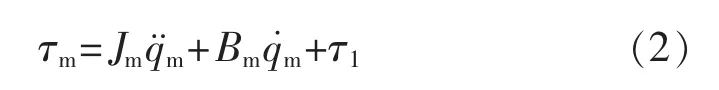
式中：τm∈Rn是电机提供的转矩矢量；qm∈Rn是电机轴的角位移；τ1∈Rn表示在电机轴上的负载转矩矢量；Jm=diag｛Jm1，Jm2，…，Jmn｝是电机轴上的转动惯量对角矩阵；Bm=diag｛Bm1，Bm2，…，Bmn｝是电机轴的粘性摩擦系数的对角矩阵。

由于每个关节是由一个直流伺服电机通过谐波传动系统驱动，我们可以得到式中：N=diag｛n1，n2，…，nn｝是一个齿轮比的对角矩阵。

直流电动机的转矩是与电枢电流成比例的。所以，我们可以得到：

式中：Kτ=diag｛Kτ1，Kτ2，…，Kτn｝是一个转矩常数的对角矩阵；u∈Rn是电动机电枢电流矢量。

式（1）～式（5）机械手的动态模型可以写成：

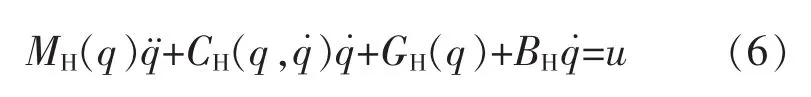
式中：

一般情况下，机械手系统的动力学具有以下三个特性：

特性1 惯性矩阵MH（q）是对称正定矩阵，存在正数 m1，m2满足

特性 2 矩阵 CH（q，）和惯性矩阵 MH（q）的导 数满足属于正实数）；

1.2 控制目标

机械手的控制目标是设计一个稳定的新型控制器，使换到机械手输出轨迹q快速准确地跟踪给定期望轨迹qd，即保证跟踪误差e在有限时间内收敛到零。qd是给定的二阶连续可导的期望轨迹，定义跟踪误差e=qd-q。

2 改进终端滑模面的设计

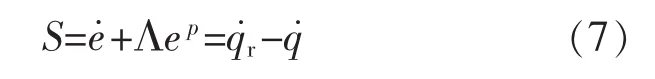
式中：；p=p1/p2，p1和 p2是正奇数满足p2＞p1，Λ是正定对角参数矩阵。

在式（7）中S的第i个元素可以写成如下形式：

当终端滑模中Si=0，表明：

从式（9）中知，ei=0 是系统（7）的终端吸引子，然后对跟踪误差ei到达零的时间tei为

是可导的，我们得到由于含有负分数幂 p-1，如果0，ei=0时，可能会引起奇异问题。

在终端滑模面上时（S=0），根据式（9）则有：

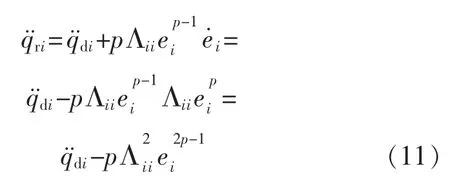
如果 p＞1/2，中就会没有负分数幂。 但是，在Si≠0和ei=0的情况下仍然存在奇异性问题。可以采用间接的方法避免奇异性问题[10]，通过切换终端滑模面和线性滑模面来避免奇异问题，但是由于简单的转换并不能完全消除奇异，提出了改进的终端滑模面。 我们首先改进为

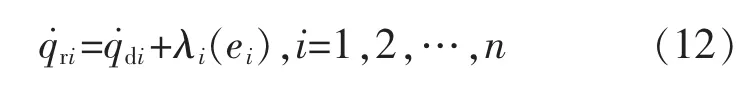
式中

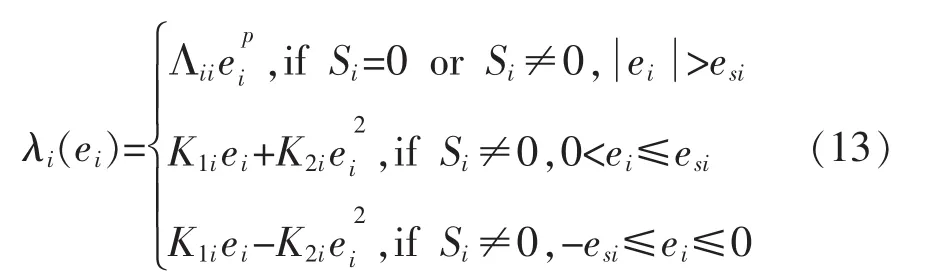
式中：是一个正常数；Λii是一个正常数。

改进的滑模面如图1所示，表示为

式中：λ（e）= [λ1（e1），λ2（e2），…，λn（en） ]T。

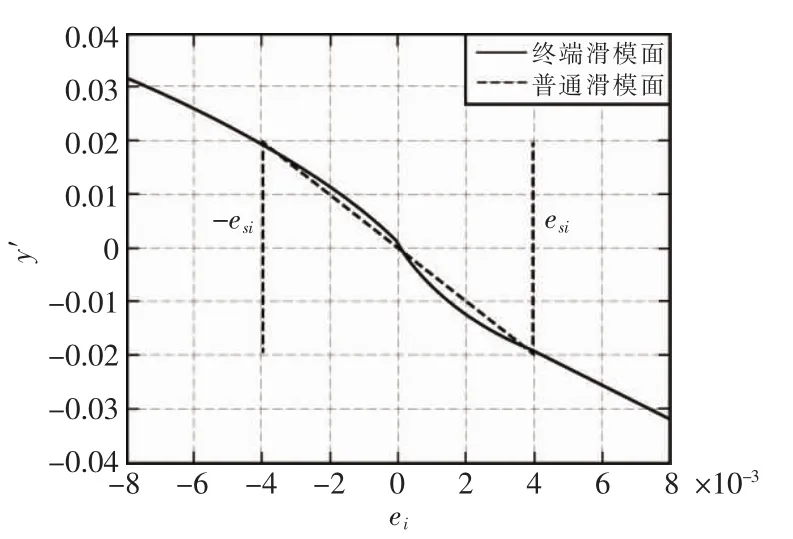
图1 改进的终端滑模面Fig.1 Improved terminal sliding surface

通过选择p＞1/2，终端滑模控制（Si=0）的奇异问题是可以避免的。在Si≠0情况下，当ei进入到|ei|≤esi区域时，从终端滑动面切换到一般滑动面上。因此，在Si≠0且ei=0的情况下，奇异性问题也可以被克服。

3 新型控制器的设计

3.1 RBF神经网络最小参数的TSMC控制器设计

由和式（8），闭环动力学公式可以写成：

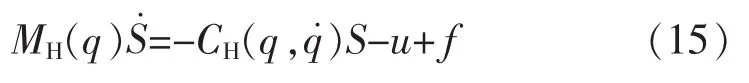
式中机器手非线性函数为

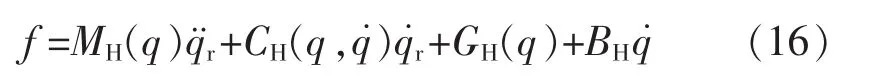
如果机器手的非线性函数f是已知的，那么控制器可以定义为

式中：K是一个正定对角常数矩阵；r=r1/r2，其中r1和r2是正奇数满足

在式 （17）中控制输入u包含一个非线性PD项，就是把式（17）代入式（8）中，我们可以得到如下的闭环系统：

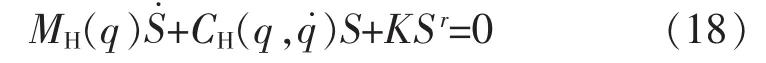
用Lyapunov理论证明闭环系统（18）的稳定性。问题是如果f的参数和结构是未知的，那么基于模型的控制器是不可用的。因此，采用RBF神经网络逼近非线性函数 f。

假设存在一个不变的理想权重矩阵w，由RBF神经网络逼近非线性函数的性质可知f可以写成：

式中：为输入向量；ε是RBF神经网络的建模误差；h（x）为常用的高斯函数。

上述控制器中RBF神经网络逼近非线性函数f中的未知参数，实现了无需模型信息的神经网络自适应控制，但是该算法不利于实时控制。那么，我们对该算法进行适当改进，采用单个参数φ，不需要基于数学模型信息，可代替RBF神经网络中的权值W，以此来实现基于单参数估计的自适应控制[11]。

取为第 i个关节点的估计权值，并且令=wi-，取单个参数 φ，令，φ 为正常数，为 φ 的估计值，

定义根据GL算子[12]，我们定义：

式中的◦表示矩阵相乘。

把式（19）可以改写成

那么控制输入u就设计为

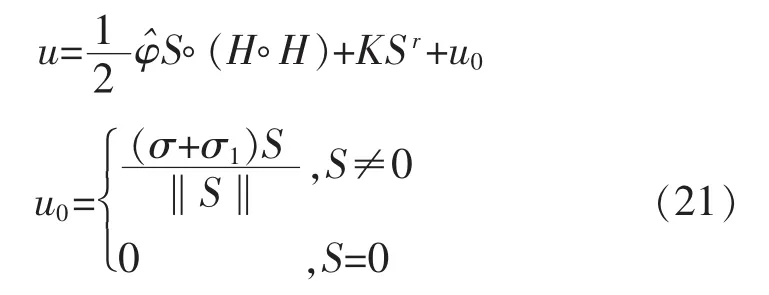
把改进的控制输入（21）代入式（6）中得：

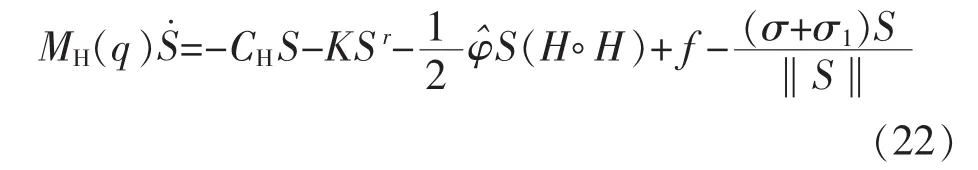
3.2 新型控制器稳定性分析

定义Lyapunov函数：

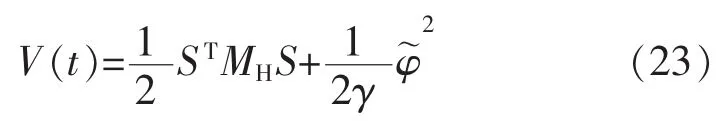
式中，γ＞0。

于是：

由于：

又由于：

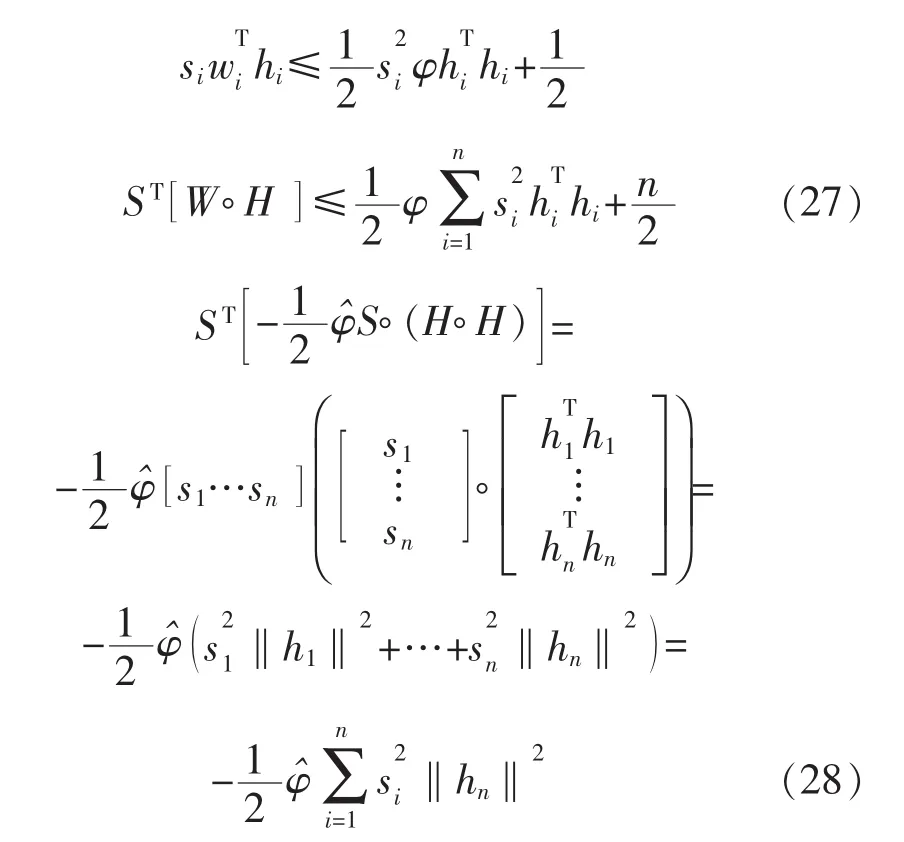
式中：n为机械手关节的个数。

于是由式（24）～式（28）计算，可以推导出式（29）为

设计自适应律为

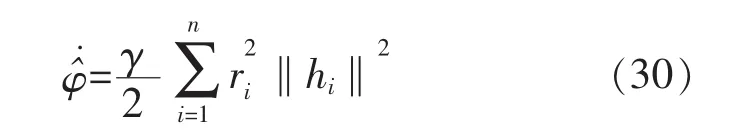
则：

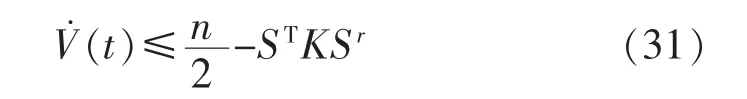
为了保证（t）≤0，只需要保证≤STKSr。经过理论推导可以证明控制器的稳定性。

4 实验结果对比

为了说明验证所设计控制算法的优点，把RBF神经网络最小参数的终端滑模控制和RBF神经网络与线性滑模结合的算法进行比较，然后通过Matlab/Simulink进行盾构机换刀机械手模型建模仿并进行仿真验证，取机械手的模型参数：

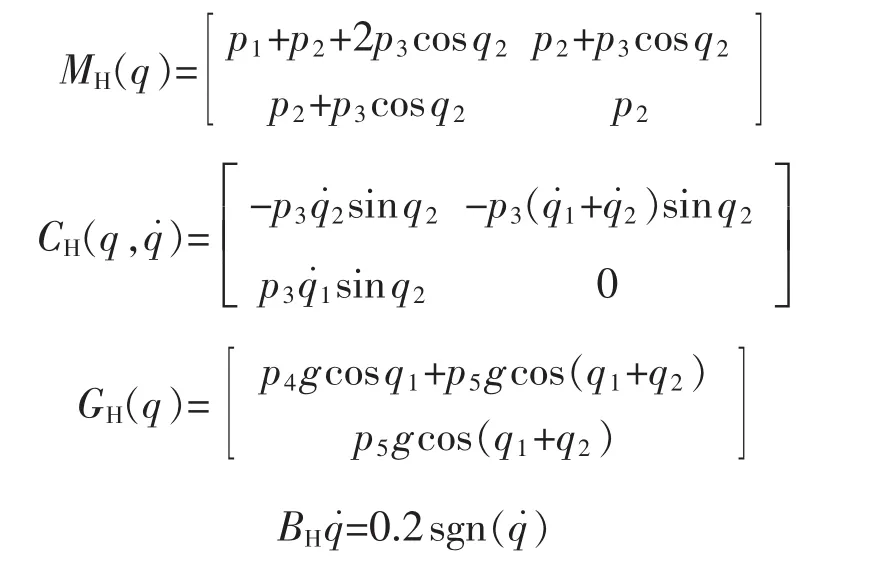
为了更好地显示动态的跟踪效果，取p=［p1，p2，p3，p4，p5］=［2.9，0.76，0.87，3.04，0.87］。 两个关节输入的期望轨迹分别是 qd1=0.05sint，qd2=0.07sint。

4.1 RBF神经网络的LSMC控制器

LSMC控制采用RBF神经网络，这种控制方案应用很广泛，控制律为

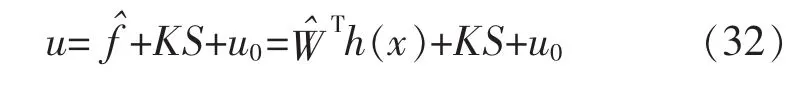
式中：

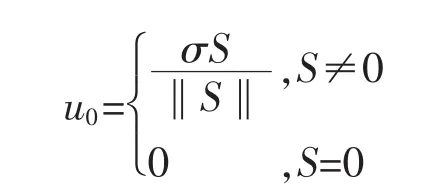
RBF网络的权重更新律为控制参数为 K=diag［30，30］，Λ＝diag［5，5］，Γ＝20，σ＝0.006。 选取模型的初始状态值为［0.09，0，-0.09，0］，仿真结果如图2～图4所示。

4.2 RBF神经网络最小参数的TSMC控制器

TSMC控制采用RBF神经网络最小参数，控制参数为 K=diag［50，50］，Λ=diag［20，20］，σ＝0.003，diag ［1，1］，选取模型的初始状态值为［0.5，0，0.5，0］，仿真结果如图5～图7所示。

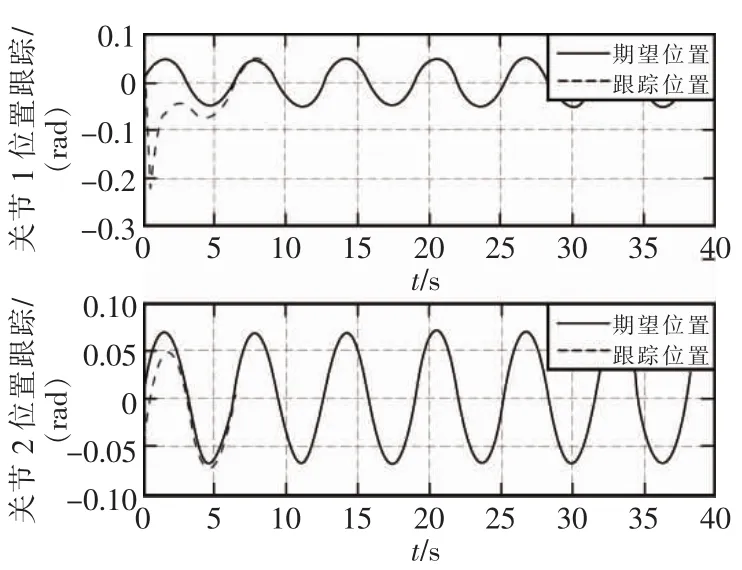
图2 RBFNN的LSMC机械手关节位置跟踪Fig.2 RBFNN LSMC manipulator joint position tracking

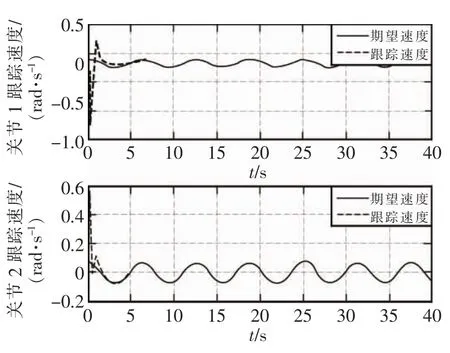
图3 RBFNN的LSMC机械手关节速度跟踪Fig.3 RBFNN LSMC manipulator joint velocity tracking

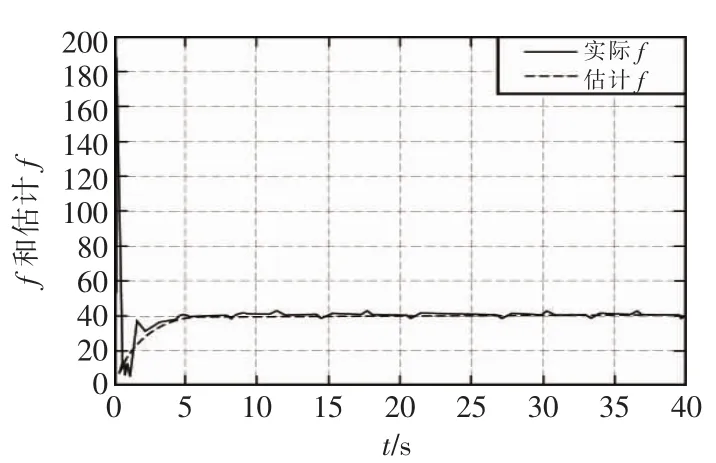
图4 RBFNN的LSMC机械手关节‖f（x）‖与逼近对比曲线Fig.4 RBFNN LSMC manipulator joint and approximation comparison curve

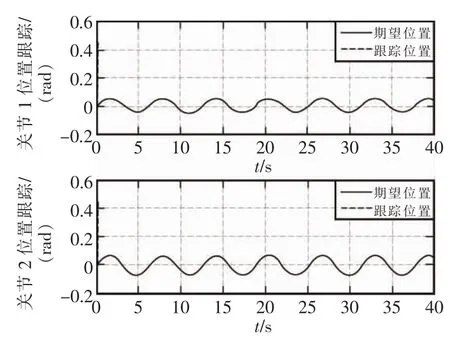
图5 RBFNN最小参数TSMC机械手关节位置跟踪Fig.5 RBFNN minimum parameter TSMC manipulator joint position tracking

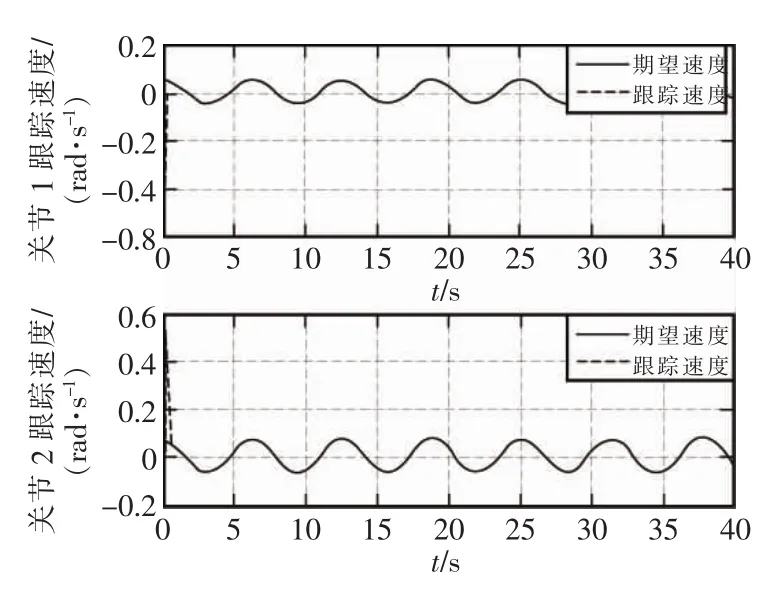
图6 RBFNN最小参数TSMC机械手关节速度跟踪Fig.6RBFNN minimum parameter TSMC manipulator joint velocity tracking

图7 RBFNN最小参数TSMC机械手关节‖f（x）‖与逼近对比曲线Fig.7 RBFNN minimum parameter TSMC manipulator joint and approximation comparison curve

两种控制器分别对两关节机械手控制的仿真结果从图中可以很明显地看出，从图2和图5对比和图3和图6对比得到，采用RBF神经网络最小参数的TSMC控制器的机械手各关节的位置跟踪和速度跟踪性能方面均不到1 s就跟踪上期望值了，而采用RBF神经网络的LSMC控制器的机械手各关节的跟踪性能都远远超过1 s。在逼近性能方面，比较图4和图7，采用RBF神经网络的LSMC控制器的机械手也没有采用RBF神经网络最小参数的TSMC控制器的机械手的逼近速度快。可以证明本文所设计的控制器在各关节位置跟踪、速度跟踪及其逼近未知参数性能方面均优于前者。

5 结语

本文提出的基于RBF网络最小参数学习法的机械手终端滑模控制方法，不依赖于机械手的精确数学模型，当机械手的结构和参数不能确定或者未知时，仍然能保证机械手系统具有良好的跟踪性能。采用改进的终端滑模面，既避免了一般线性滑模面，不能再有限时间收敛的问题，又避免了终端滑模的奇异问题；用一个单一的参数来代替神经网络的权值，简化了自适应算法，设计了性能优化的控制器；用Lyapunov理论证明了该算法的稳定性，并且用仿真的方法验证了算法的正确性、有效性和优良性。在本文的基础上，我们今后在以下方面进一步研究：我们会进一步的优化算法，并应用到机械手实体上，不断地提高该算法控制机械手实体的精度、速度和准确性。

[1] Igelnik B，Pao Y H，LeClair S R，et al．The ensemble approach to neural-network learning and generalization[J]．IEEE Transactions on Neural Networks，1999，10（1）：19-30．

[2] Lee Y，Lee C K．Classification of multiple cancer types by multicategory support vector ma chines using gene expression data[J]．Bioinformatics，2003，19（9）：1132-1139．

[3] 王艳敏，冯勇，夏红伟，等．多输入不确定系统的平滑非奇异终端滑模控制[J]．控制与决策，2015，30（1）：161-165．

[4] 刘俊龙．机械臂的神经网络自适应终端滑模控制研究[D]．沈阳：东北大学，2014．

[5] 龚发云，袁雷华，汤亮．SCARA机械手的RBF神经网络自适应轨迹跟踪控制[J]．机床与液压，2014，42（3）：41-46．

[6] F．L．Lewis，C．T．Abadallah，D．M．Dawson．Control of Robot Manipulator[S]．New York：Macmillan，1993．

[7] Yoo D S，Chung M J，Bien Z．Real-time implementation and evaluation of dynamic control algorithms for industrial manipulators[J]．IEEE Transactions on Industrial Electronics，1991，38（1）：26-31．

[8] Liangyong Wang，Tianyou Chai，Fellow，et al．Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics[J]．IEEE Transactions on Industrial Electronics，2009，56（9）：3296-3304．

[9] 刘金琨．滑模变结构控制Matlab仿真[M].1版．北京：清华大学出版社，2005．

[10] Feng Y，Yu X H，Man Z H．Non-singular adaptive terminal sliding mode control of rigid manipulators[J]．Automatica，2002，38（12）：2159-2167．

[11] 刘金琨．滑模变结构控制Matlab仿真[M].3版．北京：清华大学出版社，2015．

[12] S．S．Ge，C．C．Hang，T．H．Lee，T．Zhang．Stable Adaptive Neural Network Control[M]．Boston，MA：Kluwer，2001． ■