基于改进滑模控制的光伏系统最大功率跟踪

， ， ， ，

(1.国网河北省电力有限公司新河县供电分公司，河北 邢台 055650；2.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

0 引言

光伏电池板作为光伏发电系统中重要的能量转换元件[1]，其转换效率的高低直接影响着整个光伏系统能量的输出。光伏电池的输出是典型的非线性伏安关系，受周围环境主要是光照强度和温度的影响。为了使光伏电池的输出始终保持在最大功率点，众多学者对光伏电池的最大功率跟踪(MPPT)算法[2-3]做了各种研究。恒定电压法[4-6]是最早、最简单的一种MPPT算法，原理简单、便于控制，响应速度快，但只适合温度变化幅度较小的环境。电导增量法[7]直接关注功率变化，控制精度较高，但是对硬件的计算能力有一定的要求，否则会增加系统的控制周期。扰动观测法[8-9]是一个寻优的过程，文献[10]提出的变步长扰动观测法，减小了稳态误差，但是响应速度并没有明显提高。文献[11]提出的滑模变结构控制，跟踪速度明显提高，但是系统趋于稳态时会在滑模面出现高频率、小幅度的抖动。这些方法虽然在跟踪速度或控制精度方面均有各自的优势，但是并没有一种较好的算法能够改善这两方面的矛盾，因此对MPPT控制算法的研究很有必要。

1 最大功率跟踪的工作原理

1.1 光伏电池的基本特性

太阳能光伏电池本质上属于半导体PN结，PN结经阳光照射产生光电流的现象称为光生伏特效应。当温度为T=25 ℃，S光照强度分别取600、800、1 000W/m2时，光伏电池的U-I曲线和U-P曲线如图1、图2所示。

由图1可以看出，电压和电流呈非线性关系，在电压达到一定的值后，随电压升高，电流迅速降低，且不同光照对应的伏安特性曲线也不相同。

由图2 可知，光伏电池的输出功率随电压变化而变化，会在某一电压值附近出现最大功率点，环境不同，最大功率点也不尽相同。

图1 光伏电池的U-I特性曲线

图2 光伏电池的U-P特性曲线

1.2 最大功率跟踪的工作原理

光伏电池输出的电压幅值较小，一般先用Boost电路进行升压，最大功率跟踪正是在此电路的基础上实现的，如图3所示。

由最大功率传输定理可知，当光伏电池输出最大功率时，输出阻抗等于负载阻抗。因此，光伏电池的最大功率跟踪过程实际上就是匹配光伏电池的输出阻抗与负载阻抗的过程。当光照均匀时，由图2可知，光伏电池的P-U曲线为单峰值曲线，且在最大功率点处有

dPmax/dUmax=0

(1)

式中，Pmax、Umax分别为光伏电池输出最大功率点的功率和电压。

将图3简化为一个简单的光伏系统图，仅由光伏电池、负载R和PWM开关信号K组成如图4所示。当开关信号K的占空比D=0时，负载阻抗RL=∞；当D=1时，负载阻抗RL=R。

开关K的输入-输出关系为

Uout=UinD

(2)

则

dP/dD=dP/dUin·dUin/dD=-dP/dUin·dUout/D2

(3)

在最大功率点处有Umax=Uin，所以

dPmax/dD=0

(4)

因此可以通过改变占空比D的数值来实现控制光伏电池功率输出，即计算出Pmax处的占空比D就找到了对应时刻的Pmax。

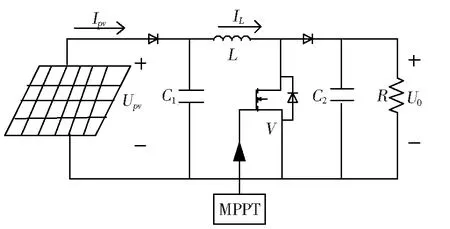
图3 Boost升压电路

图4 Boost简化电路

2 改进滑模控制器的设计

滑模变结构控制(滑模控制)是变结构控制的一种方法。这种控制方法与常规的控制策略根本性区别在于控制是不连续的，是一种随时间变化系统结构随之改变的控制特性。这种变化可以使系统在一定的状态下沿规定的运动轨迹作高频率、小幅度的上下运动，即“滑动模态”或“滑模”运动。滑动模态可以预先规定设计，与外界扰动及系统参数无关，所以滑模控制对光伏系统的MPPT有比较好的鲁棒性[12]。

传统的滑模控制器的控制变量与系统参数和外界扰动无关，响应速度快，能迅速到达最大功率点附近，但是当系统状态趋于稳定，靠近滑模面时，由于滑模不连续控制的本质，使系统来回穿越滑模面，不能保持，因而产生高频抖动。变步长的扰动观测法在到达最大功率点时将步长控制在较小值不变，几乎可以使系统保持平滑，但是在到达最大功率点的过程中，系统判断并改变步长会增加系统的响应时间。

结合以上两种控制方法的特点，提出了一种改进的滑模控制：

(1)若Upv-Um>ΔU，则使用滑模控制使系统快速到达最大功率点附近；

(2)若Upv-Um<ΔU，则使用变步长扰动观测法使系统保持平稳运行。

改进的滑模控制不仅能够削弱滑模控制的抖动问题，还能保证一定的响应速度，使光伏电池最大限度地工作在最大功率点附近。

2.1 变步长扰动观测法

图5 变步长扰动观测法的控制流程图

变步长扰动观测法是目前使用比较广泛的一种MPPT算法，占空比的改变值称为扰动步长Δd。系统刚启动时距离最大功率点较远，令Δd较大，快速接近，当功率差值缩小到一定范围内以后，适当减小Δd，以便系统稳定工作在最大功率点附近，变步长扰动观测法的流程如图5所示。

2.2 滑模控制器的设计

传统的滑模控制直接控制输出电压，而本文采用的是间接电流法，即利用电感电流的误差来控制输出电压。间接电流法能够保证系统的滑模区存在，而传统的电压控制有时不一定存在。滑模控制器的设计主要是求取滑模切换函数和控制率，并证明滑模控制率的可达性，即该控制率在滑模面上存在滑模区。设u为升压电路中开关管V的函数表达式

(5)

取切换函数为

s(x)=iL-iLref

(6)

式中，iL为Boost电路中的电感电流;iLref为稳态时Boost电路中电感的参考电流。取控制率为

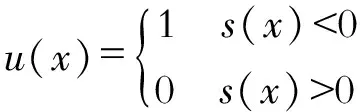
(7)

为了提高系统的响应速度和稳态误差，在式(6)中加入比例积分，形成新的切换函数。

(8)

其中

f=iL-iLref

(9)

根据赫尔维茨判定定理，系统的多项式

ɑnsn+ɑn-1sn-1+ɑn-2sn-2+…+ɑ0=0

(10)

稳定的充要条件是ɑn>0，且一般取ɑ0=1，所以，当Kp>0，Kd=1时s(x)是稳定的。

为了提高滑模控制的响应速度，采用指数趋近率

(11)

根据式(6)、式(8)、式(9)及Boost电路的基尔霍夫定律可得切换函数的导数为

(12)

解得滑模控制率为

(13)

将式(13)代入式(12)得

(14)

由此可证明

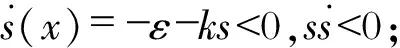
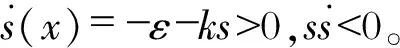
因此，该切换函数和控制率满足滑模控制的可达性条件，所设计滑模控制器能够使系统稳定于s=0。

2.3 改进滑模控制器的Simulink仿真

根据最大功率跟踪的控制原理，在Simulink中搭建了光伏电池模型和Boost电路，如图6所示，并根据改进滑模控制的切换函数和控制率对该算法进行了建模，如图7所示。

对变步长扰动观测法、传统滑模控制器以及改进的滑模控制器分别进行了Simulink仿真，得到各种控制方式下光伏电池输出功率的波形，如图8～图10所示。

由以上3个功率输出波形可以看出，当光照强度为1 000 W/m2时，变步长扰动观测法到达最终稳定电压的时间较长,约为0.08 s，但是稳定后基本保持在60 W；传统滑模控制刚好相反，由起始到达稳定状态响应时间较短,约为0.04 s，但是稳定后并不能平滑地保持在60 W上，有明显的抖动；而改进滑模控制到达最终稳定电压的时间约为0.04 s，稳定后平滑保持在60 W，消除了传统滑模控制的抖动现象。由此可以证明，改进的滑模控制综合了两种算法的优点，既保留了滑模控制的响应速度，又减少了稳定状态下的抖动，为最大功率跟踪提供了一种新思路。

图6 光伏系统MPPT仿真模型图

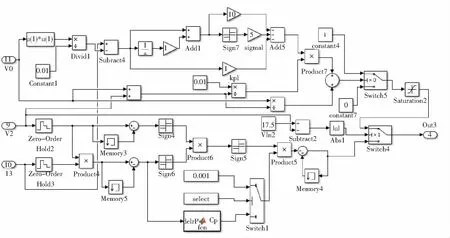
图7 改进滑模控制的Simulink模型

图8 变步长扰动观测法的功率输出

图9 传统滑模控制的功率输出

图10 改进滑模控制器的输出功率

3 基于STM32的实验

为了验证提出的改进滑模控制算法的可靠性，进行了基于STM32的硬件实验。采用两个功率为10 W的万家好JB—007太阳能光伏组件并联作为电源模块，搭建了实验平台对其输出情况进行了跟踪，如图11、图12所示。

图11 光伏组件

图12 实验平台

实验过程中，光伏电池输出电流的波形采用串联0.5 Ω电阻两侧的电压波形来代替，测得该时刻的光照强度和温度的平均值分别为S=800 W/m2，T=15 ℃，实验结果如图13、图14所示。

图13 传统滑模控制的实验结果

图14 改进滑模控制的实验结果

由图13、图14可以看出，传统滑模控制器到达最大功率点后波形的抖动较大，而改进的滑模控制抖幅明显减小，波形清晰，且改进滑模控制保留了传统滑模响应较快的特点。因此，可证明提出的改进滑模控制算法，改善了光伏系统中最大功率跟踪在跟踪速度和跟踪精度上的矛盾，可以应用到实际的系统中。

4 结论

通过对光伏电池最大功率跟踪原理的学习，对各种MPPT算法的分析比较，清楚了各种常用算法的优缺点，并在传统滑模控制的基础上提出了改进型滑模控制。根据理论推导、仿真和实验可得到如下结论：

(1)理论推导证明了改进滑模控制算法在理论上的存在性和可达性。

(2)通过仿真结果对比分析，验证了改进滑模控制能够很好地解决最大功率跟踪在跟踪速度和跟踪精度方面的矛盾，为MPPT提供了一种新方法。

(3)实验结果表明，提出的改进算法在保证响应速度的基础上减小了稳态误差，可以应用到工程实践中。

参 考 文 献

[1]徐成,赵金城,郑洪有,等. 屋顶安装光伏太阳能板风荷载试验研究[J]. 石家庄铁道大学学报:自然科学版,2015,28(2):62-67.

[2]Kasa N, Iida T, Chen L. Flyback inverter controlled by sensorless current MPPT for photovoltaic power system[J]. IEEE Transactions on Industrial Electronics, 2005, 52(4):1145-1152.

[3]Salas V, Olias E, Barrado A, Lazaro Review of maximum power point tracking algorithms for stand-alone photovoltaic arrays[J].Solar Energy Mat Solar Cells，2006， 90(11):1555.

[4]张晓辉,姜军,马红伟. 一种光伏系统最大功率点跟踪新方法及其仿真验证[J]. 南方电网技术,2013(3):71-75.

[5]熊远生,俞立,徐建明. 固定电压法结合扰动观察法在光伏发电最大功率点跟踪控制中应用[J]. 电力自动化设备,2009(6):85-88.

[6]戴志威,舒杰,吴昌宏. 基于环境参数模型的定电压MPPT控制算法研究[J]. 电力电子技术,2015 (5):61-63.

[7]杨立永，毛鹏.光伏发电系统的优化建模、仿真和控制[M].北京:北京机械工业出版社, 2014.

[8]王奇. 光伏发电MPPT控制方法研究与改进[D].秦皇岛:燕山大学,2014.

[9]吴增强. 光伏发电系统的最大功率跟踪和并网控制策略研究[D].上海:上海电机学院,2015.

[10]刘邦银,段善旭,刘飞,等. 基于改进扰动观察法的光伏阵列最大功率点跟踪[J]. 电工技术学报,2009(6):91-94.

[11]马海川. 基于滑模变结构控制的光伏发电系统控制器的设计 [D].沈阳:东北大学,2012.

[12]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.