基于字典学习形态分量分析的轴承故障诊断

， ，

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

在负载和工况变化时，滚动轴承的振动信号通常为非平稳信号，故障产生的冲击会引起不同程度和形态的振动信号调制、耦合现象，因此，如何有效地提取轴承故障特征是轴承故障诊断技术研究的重要内容。杨红娜将随机共振与共振解调相结合来提取故障特征[1]，但仅适用相对线性的系统。2004年，Starck et al[2]提出了形态分量分析方法，其基本思想是利用信号组成成分的形态差异性，不同形态的信号可以用不同的字典稀疏表示，结果把源信号分解成若干个形态各异的稀疏信号，且被分解出的各分量具有实际的物理意义。有学者用基于固定字典的MCA方法从轴承和齿轮箱的复合故障振动信号中提取出各故障特征[3-5]，取得了比较好的效果，但每个固定字典具有确定的数学模型，如Dirac字典、Fourier字典、小波字典等，不能最佳匹配被分析复杂信号的结构特征，所以在强噪声下难以提取到故障特征。最近研究成果表明，通过学习获得的字典比固定字典在图像去噪、图像修复、图像超分辨率等方面有更出色的性能[6-7]，Liu et al[8-10]提出一种移不变的稀疏编码进行字典学习并应用于轴承故障诊断。因此，如果根据故障信号本身学习出振动信号中包含故障特征的波形函数作为字典，无疑会促进形态分量分析方法对故障特征的提取。

根据以上分析，将MCA方法与K-SVD字典学习算法相结合，提出了基于字典学习形态分量分析的轴承故障诊断方法。采用K-SVD算法对轴承内圈、外圈故障信号的训练样本进行学习，获得能够对故障信号进行稀疏表示的字典；将学习到的字典替换表征冲击成分的Symlet小波字典，使用MCA对复杂信号提取故障特征分量；对包络后的故障特征分量做频谱分析，诊断轴承的故障及部位。研究结果表明：在采提取故障特征时，K-SVD学习到的字典优于构造的固定字典。

1 MCA介绍

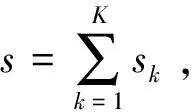
(1)

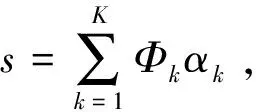
(2)

(3)

(4)

通过以上过程将原始信号分解成表示不同特征的信号分量。

2 K-SVD原理

∀i，‖xi‖0≤T0

(5)

式中，T0为稀疏表示系数中非零元素个数的最大值。K-SVD字典学习技术的具体实施步骤为[7]

(1)字典初始化。初始字典使用部分原数据，设置字典矩阵D(0)∈Rn×K，并用ρ2范数对字典的每一列单位标准化。

(2)稀疏编码。根据初始字典D，采用任意一种追踪算法(选用正交匹配追踪(OMP))，求解每个样本yi的稀疏系数向量xi，即

(6)

(7)

通过式(7)来优化字典空间，完成字典的学习过程。

3 字典学习形态分量分析的轴承故障诊断

基于字典学习形态分量分析的轴承故障诊断方法步骤如下：(1)分别以含有单个故障特征的信号为训练样本，利用K-SVD算法对训练样本进行学习，得到每个故障特征的字典；(2)使用学习到的字典替换固定字典，将复合故障的信号作为测试样本进行MCA分解，得到包含轴承外圈、内圈故障特征的冲击分量；(3)对各个冲击分量做Hilbert变换得到各自的包络谱；(4)根据各自故障特征频率结合包络谱诊断轴承故障。

4 算法仿真及对比

设置如下含有两种成分的信号进行仿真分析(采样频率为4 096 Hz，采样点数N为2 048)

s(t)=h(t)+y(t)+n(t)

(8)

h(t)=A·cos(2πfit)

(9)

(10)

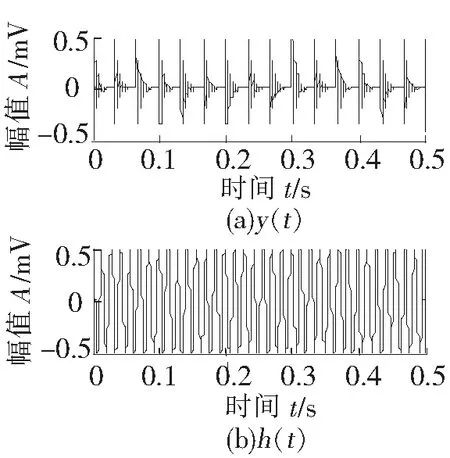
图1 冲击与简谐的仿真信号

式中,h(t)为余弦信号;幅值A是0.5;特征频率fi为70 Hz；y(t)为冲击信号;幅值B取0.5;阻尼系数g取0.1;固有频率fn为270 Hz;重复次数K取15，合成后冲击信号的特征频率为30 Hz。两种成分的信号如图1所示，加入噪声信号n(t)并调整其信噪比为6 dB，复合信号如图2(a)所示，可见复合信号中的冲击特征被噪声淹没。使用固定的字典，构建离散余弦字典来稀疏表示信号中的简谐成分，构建8阶消失矩Symlet小波字典来稀疏表示信号中的冲击成分。对复合信号s(t)进行形态分量分析，结果如图2所示，其中图2(c)为分离出的冲击成分(Part1)，对比图1(a)可知冲击成分未被完全分离出，对Part1进行Hilbert包络解调做谱分析，如图3(a)所示，在其频谱图中未找到特征频率；图2(d)为分离出的简谐成分(Part2)，与图1(b)对比可知两种信号的形态接近，对Part2直接进行傅里叶变换如图3(b)，在70 Hz处出现一个峰值，与简谐信号的特征频率一致；图2(b)为Part1与Part2的叠加，其形态与复合信号相似。经以上仿真试验可知，基于固定字典的形态分量分析在强噪声情况下不能有效分离出复合信号中的冲击成分。

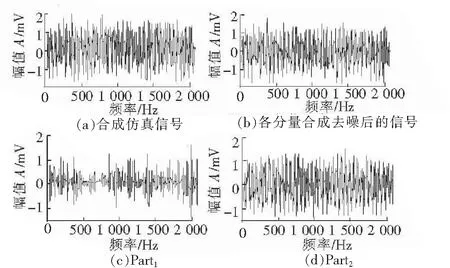
图2 形态分量分析方法分解信号结果

图3 各分量的频谱图

使用本文提出的方法，以冲击信号、余弦信号作为训练样本，使用K-SVD算法对训练样本进行学习，将学习到的字典替换Symlet小波字典和离散余弦字典，应用MCA方法分解复合信号，结果见图4。在图4(c)中能够找出冲击成分，对其做Hilbert包络谱分析，如图5(a)所示频谱图发现冲击成分的特征频率30 Hz及其倍频成分；图4(d)为分解出的简谐成分，虽然出现了调幅现象，但从形态上更接近图1(b)。以上分析说明K-SVD方法学习到的字典比固定字典更能稀疏表示源信号。

图4 改进算法后分解到的各个分量

图5 改进算法后各个分量的频谱图

5 应用实例

实验轴承型号为SKF6205在轴承外圈、内圈上使用电火花机床分别加工了直径为 0.18 mm、深 0.28 mm 的凹槽，故障特征频率见表1。

表1 SKF6205轴承在不同负载下故障数据

复合故障信号如图6(a)所示，使用固定的字典，构建8阶消失矩Symlet小波字典来稀疏表示信号中的冲击成分。对复合故障信号进行MCA分解，结果如图6所示，图6(b)为去噪后的信号，图6(c)为分离出的外圈分量，图7(d)为内圈分量，可知外圈的冲击成分丢失，内圈分量的包络谱中同时包含了内圈与外圈的特征故障频率成分，不能分离出内、外圈的故障特征。

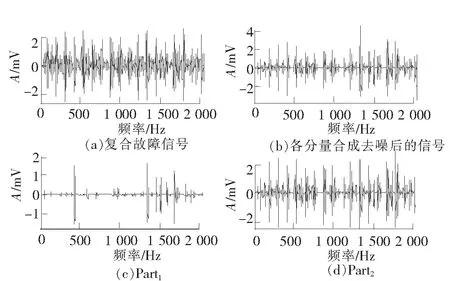
图6 固定字典MCA分解到的各个分量

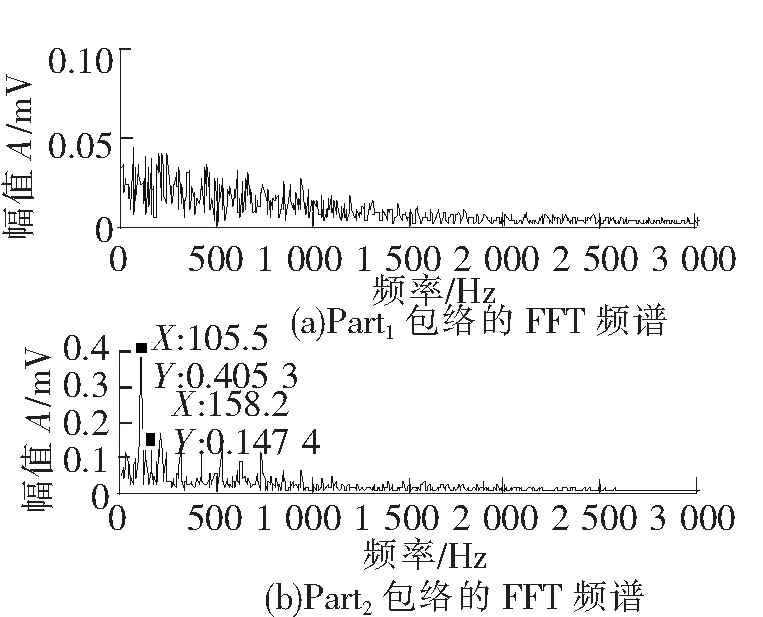
图7 固定字典MCA分解到的各个分量包络谱

分别以外圈故障数据b、内圈故障数据e为样本信号，使用K-SVD算法学习字典，将学习到的字典替换固定字典，分解信号结果如图8(c)、图8(d)所示。图8(c)为外圈分量，其包络谱见图9(a)，出现105.6 Hz及其倍频成分，与表1中的外圈理论故障特征频率105.86 Hz一致，图8 (d)为内圈分量，其包络谱见图9(b)，158.2 Hz处有峰值，与表1中的内圈理论故障特征频率157.96 Hz一致。

图8 学习字典的MCA分解到的各个分量

图9 学习字典的MCA分解到的各个分量频谱

将以上的复合故障信号加入噪声，调整其信噪比为0 dB，加噪声后的信号见图10(a)，再次使用字典学习的形态分量分析方法，结果如图10(c)、10(d)和图11所示，可知，信噪比为0 dB时，仍可成功提取出外圈、内圈的故障特征波形。但图9(a)的峰值及其倍频成分显然比图11(a)清晰，调整原始信号的信噪比为-3 dB时，则在频谱图中难以找到故障特征频率及其倍频成分(限于篇幅不再列出-3 dB时的频谱图)。可知原始信号的信噪比大小影响诊断的结果，信噪比较大的样本能训练出更加匹配信号的字典，从而实现故障诊断。

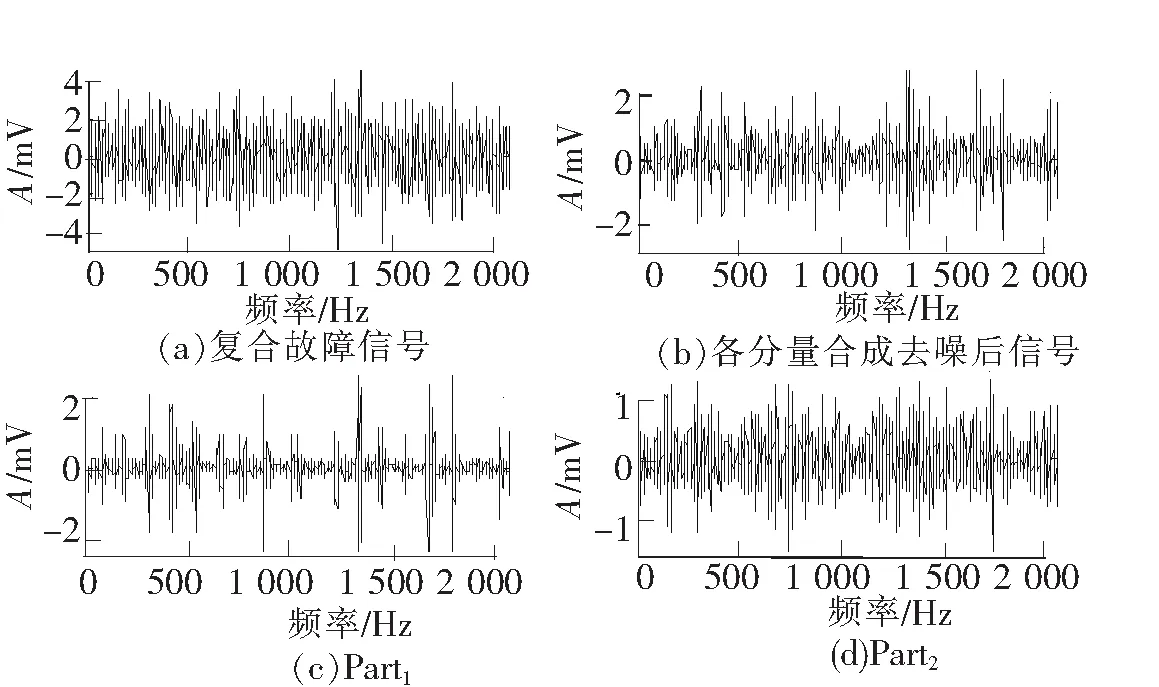
图10 强噪声下分解到的各个分量

图11 强噪声下分解到的各个分量频谱

再使用2 HP负载工况下学习到的字典，以1 HP负载下复合故障信号为测试样本，使用本文提出方法分解信号。图12中(c)、(d)分别为外圈、内圈分量，在各自的频谱图(图13(a)、图13(b))中同时找到外圈与内圈的故障特征频率，但出现频率混叠现象。

在使用K-SVD训练字典时，选取的样本信号故障特征明显。

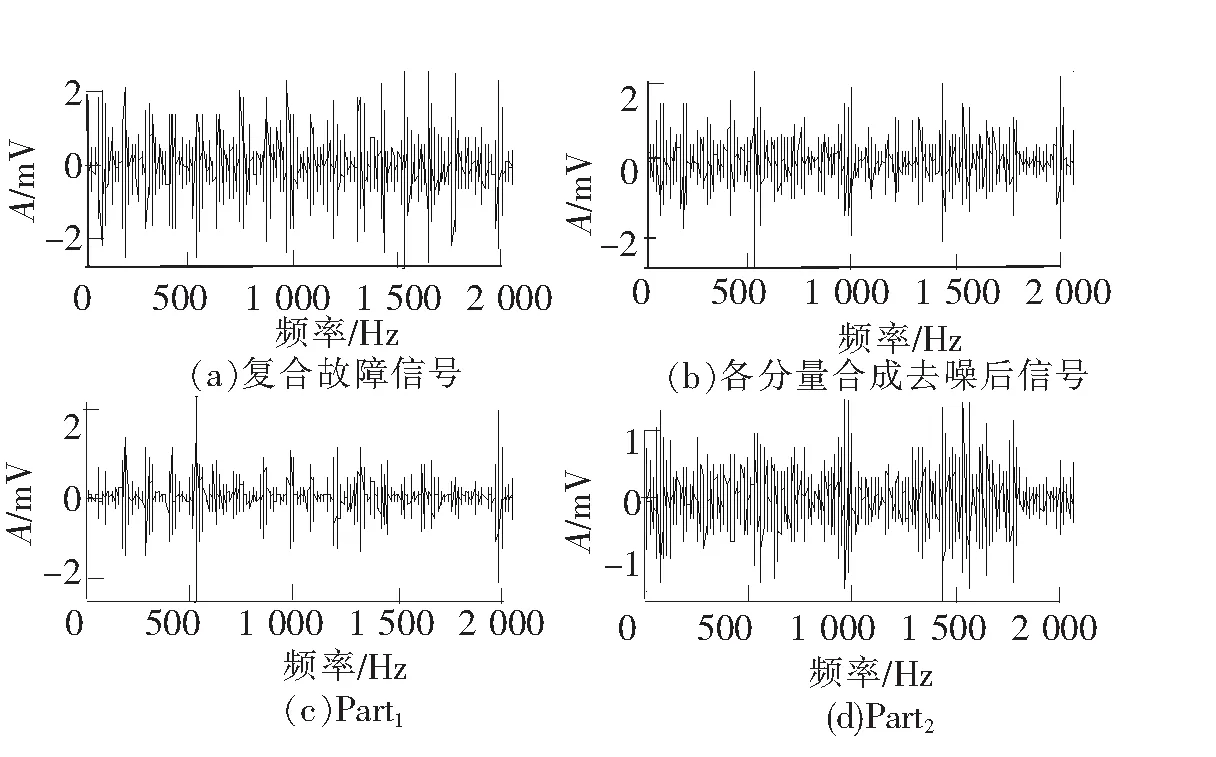
图12 1 HP负载下分解到的各个分量

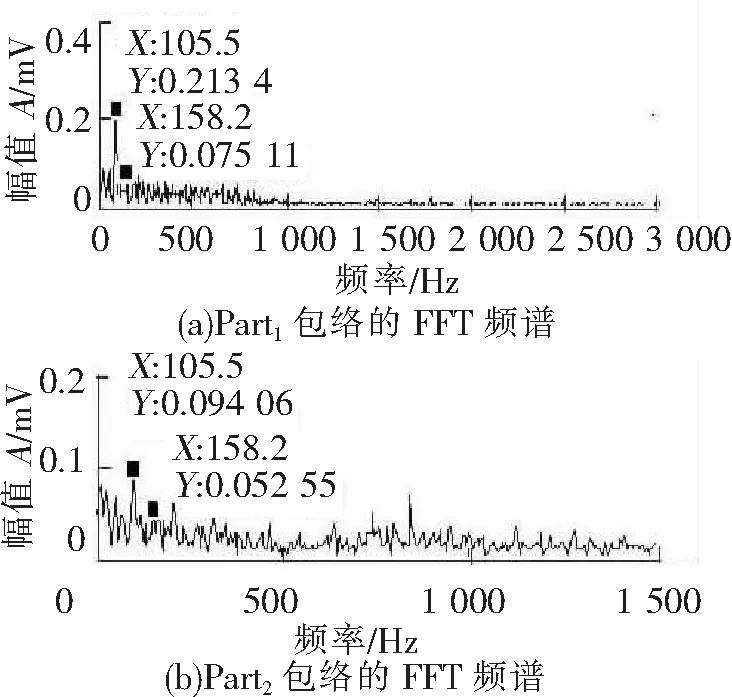
图13 1 HP负载下分解到的各个分量频谱

6 结论

在基于固定字典的形态分量分析方法基础上，提出了字典学习形态分量分析的滚动轴承复合故障诊断方法，用于从滚动轴承复合故障信号中提取出包含轴承外圈、内圈的冲击成分，主要研究结论如下：

(1)算法仿真表明，在强噪声情况下，通过学习得到的字典比固定字典更能匹配复杂信号的结构特征；应用实例表明，利用字典学习的形态分量分析方法对滚动轴承故障振动信号进行分析，能有效地提取滚动轴承复合故障信号中的冲击成分。

(2)在强噪声或某种负载下，学习到的字典能够提取出该种工况下轴承外圈、内圈故障波形；在不同工况下的故障特征提取时，虽然在各自的频谱图中能够找到外圈与内圈的故障特征频率，但出现了频率混叠现象，需进一步研究解决。

参 考 文 献

[1]杨红娜, 郝如江. 基于随机共振的齿轮箱早期故障诊断研究[J]. 石家庄铁道大学学报:自然科学版, 2016, 29(2):61-66.

[2]Starck J L, Moudden Y, Bobin J, et al. Morphological component analysis[J]. Journal of the Brazilian Computer Society, 2004, 10(3):31-41.

[3]杨杰, 郑海起, 关贞珍,等. 基于形态成分分析的轴承复合故障诊断[J]. 轴承, 2011(8):38-42.

[4]陈向民, 于德介, 李蓉. 齿轮箱复合故障振动信号的形态分量分析[J]. 机械工程学报, 2014, 50(3):108-115.

[5]李辉, 郑海起, 唐力伟. 形态分量分析在齿轮箱复合故障诊断中的应用[J]. 振动、测试与诊断, 2013, 33(4):620-626.

[6]Michael E, Michal A. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2007, 15(12):3736-3745.

[7]Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11):4311-4322.

[8]朱会杰, 王新晴, 芮挺,等.基于稀疏编码的振动信号特征提取算法与实验研究[J]. 振动与冲击, 2015, 33(21):59-64.

[9]Grosse R, Raina R, Kwong H, et al. Shift-invariance sparse coding for audio classification[J]. Computer Science Learning, 2012(9):149-158.

[10]Liu H, Liu C, Huang Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J]. Mechanical Systems & Signal Processing, 2011, 25(2):558-574.