结合深度学习的机械臂视觉抓取控制
2018-06-28白成超宋俊霖
白成超,晏 卓,宋俊霖
(1.哈尔滨工业大学航天工程系,哈尔滨150001;2.西安航空动力试验技术研究所,西安710000)
1 引言
人类航天活动产生了大量的空间碎片和太空垃圾,严重威胁航天器的正常运行,有必要对其进行监控管理和回收[1]。机械臂是完成这个任务的重要工具,可以抓取接近航天器的太空垃圾,使其脱离轨道,从而有效地保护航天器[1]。机械臂抓取目标首先需要知道目标的位置,这就需要利用传感器检测与识别技术识别出目标,同时计算出其准确的空间位置,因传感器的类型不同,识别原理也不同,本文主要基于相机来研究视觉精确识别。
机械臂视觉抓取在常规的机器人学、控制理论的基础上,融合了计算机视觉理论、深度学习和人工智能等学科,具有重要的科研和应用价值[2]。其中涉及的目标检测技术在视觉领域是现在非常热门的研究方向,传统目标检测通常是静态检测,而且目标单一,目标检测受到外形、大小、视角的变化以及外部光照的变化等因素的影响,因而所提取的特征泛化能力不强,鲁棒性较差,通常需要对每一个特定目标都提出相适应的算法[2],难以适应新物体。
基于深度学习的目标识别与定位是近年来的研究热点,尤其是深度学习中卷积神经网络的发展直接促进了目标识别和定位任务的进步。近几年的CVPR、ECCV等国际计算机视觉顶级会议不断有新的深度学习网络模型提出,并不断刷新各种大规模图像竞赛的精度。目标检测的精度和速度是两个主要的问题,基于区域选择的R⁃CNN系列网络与 End⁃to⁃End的 YOLO、SSD 等网络在速度和精度上均有较大的进步[3]。
机械臂视觉抓取系统中基于深度学习的视觉识别可通过对深度卷积神经网络的训练实现多目标快速识别而不必更改识别算法。这需要搜集被检测目标的大量图像制作标准的训练集,利用前述基于深度神经网络的目标识别算法对数据集进行离线训练,将得到的模型用于在线识别。R⁃CNN系列算法[3⁃4]是目前主流的用于机械臂抓取的深度学习目标检测算法,但是速度上并不能满足实时的要求。本文基于回归的思想搭建深度神经网络,并通过改进YOLO算法进行识别率及实时性的验证,即在小样本环境下,给定输入图像,直接在图像上回归出目标位置和目标类别,并同时满足实时检测的要求。
2 基于深度学习的多目标识别算法
本文用于机械臂待抓取目标识别的深度学习多目标识别算法使用YOLO算法[3],其流程如图1所示:
1)采集摄像头原始图像,将原图划分为S×S的网格。
2)每一个网格会预测 B个 bounding box(Object在图片所占的矩形框,下面记为bbox)和confidence(置信度)得分,记录的五元素具体为(x,y,w,h,P(Object)∗IOU), 其中 P(Object) 表示当前位置是一个Object的概率,IOU预测的是重叠概率。其中x、y是中心坐标;w、h是bbox的宽度和高度。
3)计算每一个网格预测的类别概率Ci=P(Classi|Object)。
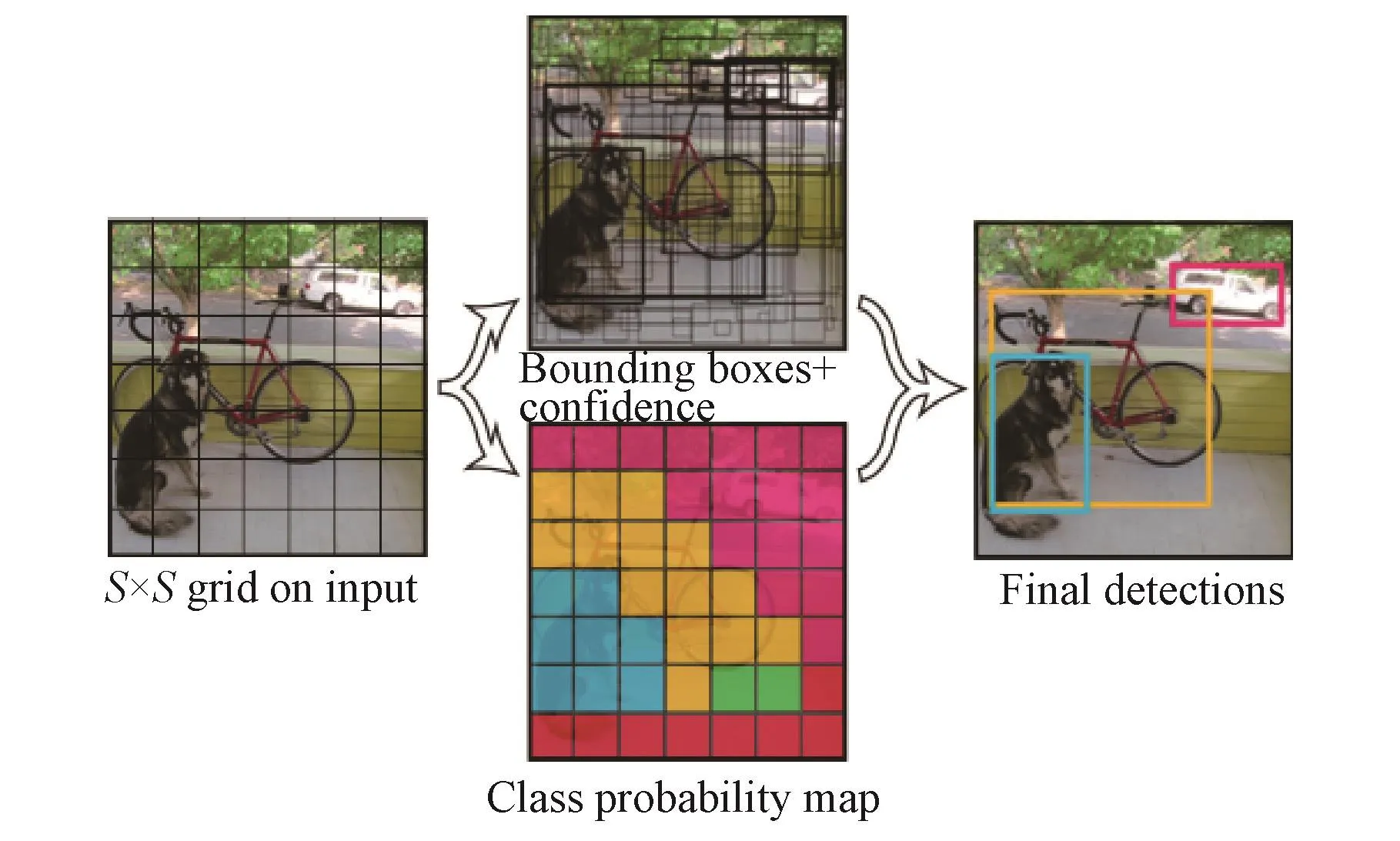
图1 YOLO算法流程Fig.1 Flow chart of YOLO algorithm
YOLO算法利用卷积神经网络实现目标识别模型,并在PASCAL VOC数据集上进行评估。网络的初始卷积层从图像中提取特征,而全连接层预测输出类别概率和相应图像坐标。网络结构参考同样应用于图像分类的GoogLeNet模型[4],有24个卷积层,然后是2个全连接层,如图2所示。
在网络训练误差中,大bbox和小bbox权值相同。另外,网络训练误差的度量方式应该反映出大bbox的小偏差与小bbox的小偏差相比更不显著。为了解决这个问题,回归的是bbox宽度和高度的平方根,而不是直接的宽度和高度。YOLO在每个网格中预测出多个bbox。在训练网络时,对每个类别,只需要用一个bbox来负责该类别的所示,涉及的D⁃H参数及各轴惯性参数可参考用户手册[5]。

图2 YOLO算法使用的卷积网络[3]Fig.2 Convolution networks for YOLO algorithms[3]
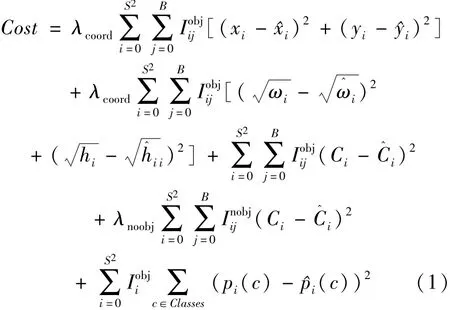
回归[3]。网络输出得到的代价函数如式(1):
如果目标在网格,损失函数会惩罚分类错误。如果预测器起作用,该损失函数也惩罚bbox的坐标误差。训练结束后通过该回归方程便可以实时预测目标类别及目标在图像坐标系中的坐标,通过计算其中心深度得到目标在相机坐标系中的三维位置。

图3 WAM 的 4⁃DOF 和 D⁃H 坐标系[5]Fig.3 WAM 4⁃DOF dimensions and D⁃H frames[5]
3 机械臂控制系统设计
3.1 机械臂系统
本文所用到的机械臂是4自由度Barrett WAM机械臂,其结构(未安装机械手时)如图3
3.2 相机与机械臂标定
上述基于深度学习的目标识别算法获得目标坐标在相机坐标系下,而机械臂的运动和控制基于的自身参考坐标系,因此需要将相机坐标系下的三维点转化为机械臂坐标系下的三维点,这个过程需要进行标定。
在机械臂与摄像机标定问题中,可由机械臂内部传感器得到机械臂末端执行器在机械臂坐标系下的三维坐标,通过双目立体视觉计算出末端执行器在摄像机坐标系下的三维坐标(通过第二章得到)。操作机械臂改变末端执行器位置我们便可以得到一组点在不同坐标系下的坐标值。
问题转化为已知空间中的同一组点在不同坐标系(摄像机坐标系、机械臂坐标系)下的坐标א= {(Xi,X′i)}, 计算两个坐标之间的变换矩阵。Xi是由齐次向量表示的第i个三维点,X是4×N矩阵包含了N个点,这些点均由齐次向量表示。得到一组对应点后,问题变成在3D刚性场景的找最优Γr的点云配准问题,可以为式(2)所示最小二乘问题:

Γr需要满足SE(3)的所有约束。利用李群结构SE(3)及其相关李代数se(3)可以将约束问题可以转化为无约束优化问题。定义代价函数如式(3):

其中 C(ω,v) =d(exp(ω,v)Xi,X′), 为了后面计算 Jacobian矩阵方便,令 d(·,·) =‖·‖2L2。
在对代价函数化简之前,有必要对输入数据进行规范化操作。这有利于防止收敛到错误的解,且减少所需的迭代次数。分别对点集X和X′计算如下转换矩阵:
对所有点进行规范化操作i= wXi,′i=w′X′i。对规范化后的点进行后续优化操作,当找到最优的 (,)∗时,真实的最优解可通过式(4)计算:
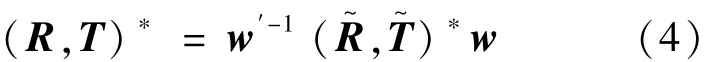
求代价函数对 se(3)的Jacobian矩阵如式(5):
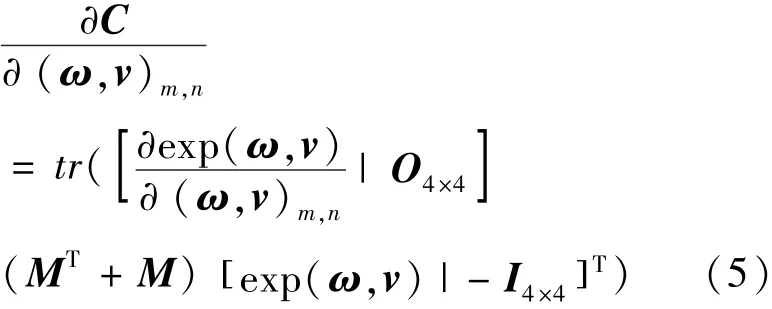
将上述算法记为算法3,其流程总结如下:
1)将X和X′标准化,并且计算w和w′;
2)生成标准化后的点集,∀i= wXi,′i= w′X′i;
3)利用标准化后的点集X和X′计算M;
4)x随机取一组数x0∈R R6,满足‖x0‖ <π,其中x为优化变量 ω,v( );
5)利用梯度下降法优化代价函数,不断迭代x直到它收敛于x∗;
6) 利用 exp将 x∗映射到 SE(3),得到(,)∗。
(R,T)∗= w′-1(,)∗w, 算法结束,得到摄像机坐标系与机械臂坐标系之间的变换关系。在第二章通过深度学习算法可以获得目标在摄像机坐标系下的三维坐标,利用这里的位姿变换关系可以转化为机械臂坐标系的三维坐标,这样便可以用于后续机械臂的路径规划即期望轨迹的计算。
3.3 期望轨迹计算
利用前述系列算法已经可以获得目标在机械臂坐标系下的三维坐标,现在将为机械臂从初始点到目标点规划一条合理的路径,这里采用MoveIt!工具包[6],运动规划算法基于第三方运动学库 OMPL(Open Motion Plan Library)。
利用Rviz和MoveIt!使模型在ROS系统进行运动仿真时可视,这样的话,给定机械臂末端执行器的起点和终点位置及姿态,OMPL库就可以在线完成运动规划。机械臂模型利用MoveIt!在从初始位姿到目标位姿的运动规划仿真如图4所示。
3.4 基于李群李代数的机械臂动力学模型
机械臂逆动力学通常用于计算使动力学系统沿着规定的关节轨迹运动所需的关节力矩,假设机械臂各关节角及角速度(θ,θ·)已知(期望轨迹计算)。通过给定的关节加速度θ¨计算关节力矩τ。另一方面,机械臂正动力学通常用于积分加速度得到系统下一个时间步长的状态(θ,)仿真系统的运动[7-9],利用给定的关节力矩 τ 计算关节加速度。定义如下变量:

图4 利用MoveIt!完成运动规划Fig.4 Motion planning made by MoveIt!
i:第i个关节的索引;
λ(i):第i个关节父关节的索引;
μ(i):第i个关节子关节的索引;
{i}:第i个关节的固连坐标系;
T:坐标变换矩阵;
Ii:第i个关节的广义惯量;
Vi:{i}系下第i个关节的广义速度;
Fi:第i个关节所受的广义力;
令将逆动力学算法记为算法1,计算逆动力学的算法包含下面两个递推过程,总结如下:
1)前向递推

2)反向递推

将正动力学算法记为算法2,计算系统正动力学的算法包含三个递推过程。假设机械臂各关节角及角速度已知(期望轨迹计算)。通过给定的关节加速度计算关节力矩。
递推过程如下:
1)前向递推
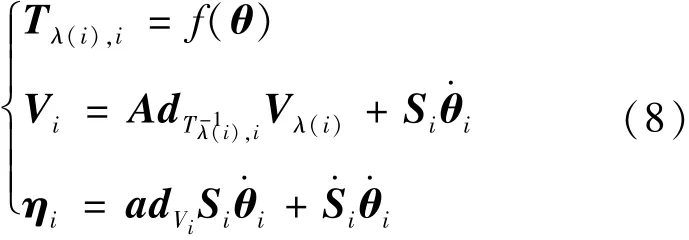
2)反向递推

3)前向递推
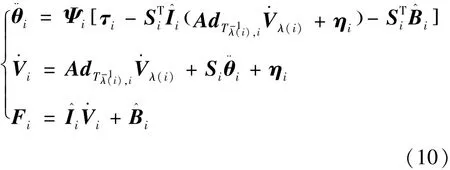
3.5 滑模控制律
相比于其他非线性控制方法,滑模控制主要优点是对动力学建模误差和外部干扰具有良好的鲁棒性[10]。 将机械臂动力学方程(6)、(7)总结如式(11):
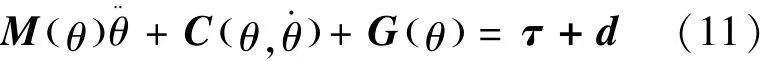
其中d为干扰力矩向量,表示机械臂真实动力学模型与名义动力学模型的偏差。下面给出两个假设[11]:
1)‖M-1(θ)‖≤α,这里α为有界正常数。
2)干扰力矩向量d= [d1d2d3d4]T也是有界的,即 ‖di‖ ≤ βi,i = 1,2,3,4。
这样机械臂动力学模型可以用式(12)表示:

定义跟踪误差:e≜x-xd,设滑模面为式(13):

这里 λ = diag(λ1,λ2,λ3,λ4),λ1、λ2、λ3、λ4为正常数。首先需要设计控制律u使得S趋于O。设计Lyapunov函数如式(14):

这里 Κ = diag( k1,k2,k3,k4),k1、k2、k3、k4为正常数。将u代入得式(17):
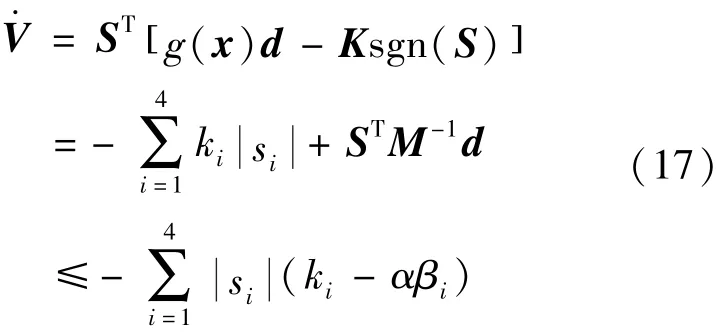
对时间求导得加速度矩阵如式(15):
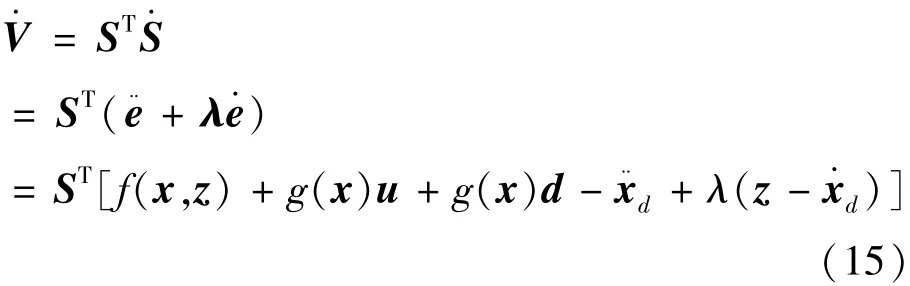
从而控制律可设计为式(16):

如果满足 ki> αβi, 将有V·< O, 这样便保证了系统在Lyapunov意义下是稳定的,即保证跟踪误差会收敛于0。代入公式(16)可得式(18):
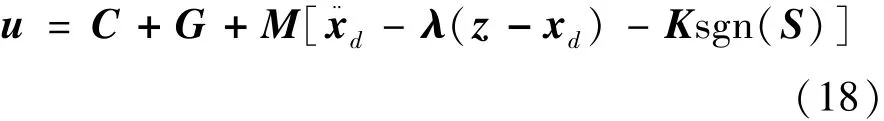
滑模控制有一个非连续项K sgn(S),当选取合适的K时它将使得滑模控制对干扰具有鲁棒性。但是,另一方面,该项也带来了抖震,为了减小抖震,使用边界层方法,即用si/( si+ε)代替sgn(si),这里ε代表边界层宽度。
4 机械臂抓取试验系统的相关验证
4.1 抓取系统简介
本系统设计方案考虑到双目摄像机能够从不同角度实时获取目标物体的图像信息,以便可以较为容易地得到目标的三维坐标,故而采用双目视觉系统。从系统工作的实时性考虑,采用固定摄像机的结构,减少系统的计算压力,提高相应速度,并且将双目相机固定在机械臂工作台的一侧,并且从安全稳定性考虑,将其放在机械臂操作空间之外。搭建的基于视觉的机械臂控制系统如图5所示,主要由两大核心部分组成:视觉目标识别系统和机械臂控制系统。
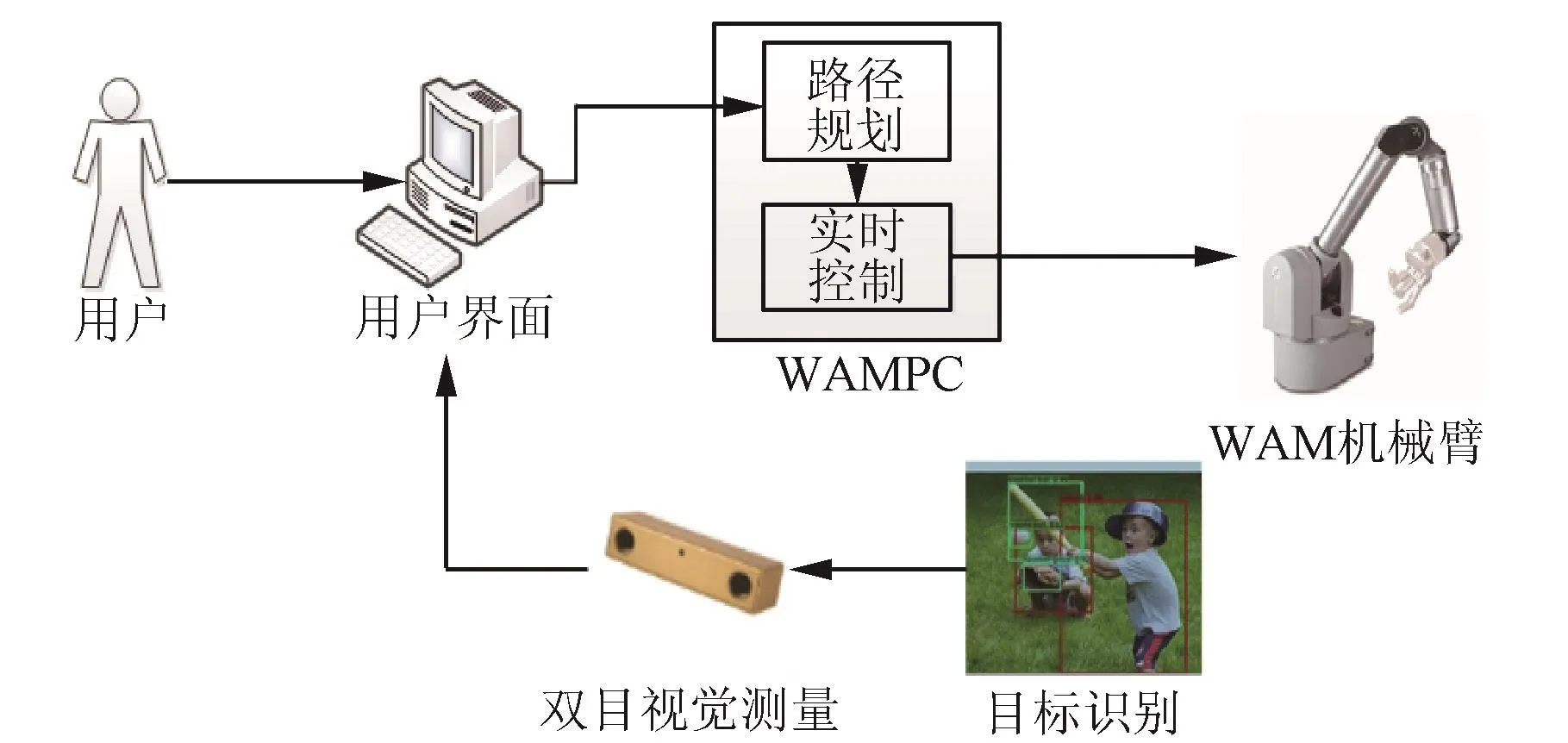
图5 抓取系统方案Fig.5 Scheme of capture system
在操作机械臂前提前利用深度学习算法训练好多目标识别模型,采集需要辨识的目标图像,构建数据集,利用数据集对深度卷积神经网络训练,并通过正则化及非凸优化调整网络权值,提高网络泛化能力。系统上电后,双目摄像头采集视频信号将图像信息传送至上位机,上位机对采集的图像信号分析,利用已经训练好的深度卷积神经网络实现目标的识别,通过双目视觉系统得到所需的目标物体的位置信息,上位机在得到目标位置信息后通过机械臂运动学逆解或者轨迹优化算法计算得到机械手欲达到这个位置每个关节需要转动的角度,根据控制算法实时计算控制器输出,通过上位机软件发出相应的控制指令驱动机械臂控制系统的控制器使各关节转动相应的角度,以使机械手准确抓取指定物体。
下面主要验证基于深度神经网络的多类目标识别与定位、机械臂的滑模控制以及避障抓取目标。
4.2 目标识别试验
考虑NVIDIA公司的 Jetson TX1(图6)具有Teraflops级的浮点计算能力和强大的软件堆栈以及超低能耗,足以负载实时目标识别的应用和开发,因此本文所用基于深度学习的YOLO算法使用此板卡实现。

图6 TX1的GPU板卡及开发者套件[12]Fig.6 TX1 GPU board and Developer Suite[12]
YOLO所依赖的深度学习框架为darknet,模型训练所需的超参数设置如下:1)基础学习率learning_rate 为 0.001;2) 学习率的衰减策略 pol⁃icy为“steps”,步长 stepsize 为 40000;3) 学习率的变化比率 scales为0.1;4)最大迭代次数 max_batche为 80200;5) 动量 momentum 为 0.9;6) 权重衰减项 decay为0.0005。
识别算法神经网络结构如表1所示。
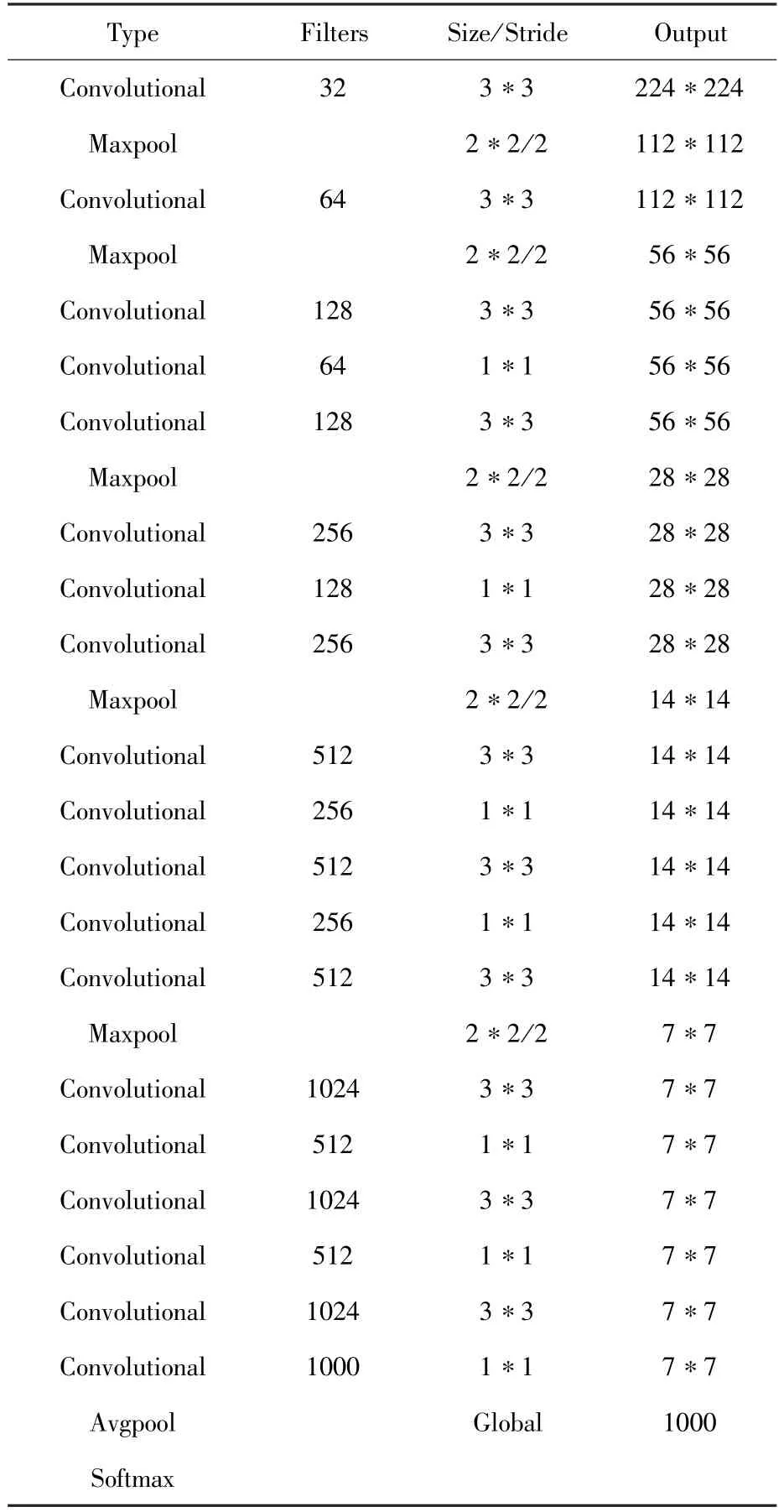
表1 网络结构Table 1 Network structure
训练过程如下:
1)首先是数据的准备,目前验证目标识别算法可以通过一些标准数据集,如Kitti数据集。如果数据集不标准,需要将数据集转化为标准数据集的形式,常见的有VOC格式。
2)然后通过YOLO算法训练神经网络连接权值,生成权值文件,这个训练过程可以通过TX1的GPU加速。
通过图7所示结果可以看出,YOLO算法识别出了包括显示屏、椅子、杯子、人等对象,对多类目标实现了较好的识别与较精准的定位。

图7 测试结果Fig.7 Test results
4.3 滑模控制验证
针对本文所用滑模控制律,首先设计一个仿真算例。该示例用于跟踪一个参考轨迹 θd(t),其表达式为: θd(t) = [0.1 + 0.5sin0.6 t -1.5708 0 3.14]T, 设 初 始 条 件 为 θ(0) =[0 - 1.5708 0 3.14]T, 控制律的相关参数为: λ = 20Ι4×4、Κ = 25Ι4×4、ε = [0.5 0.5 0.5 0.5]T, 仿真的采样时间为 0.001 s。 得到图 8 所示结果。
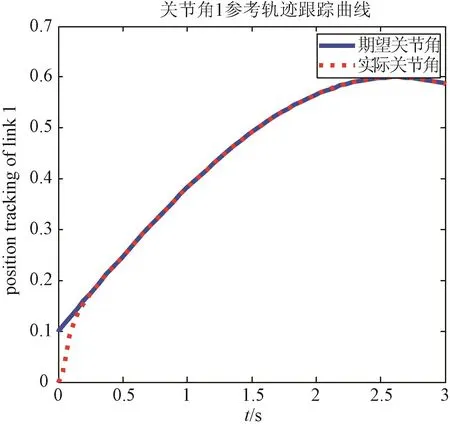
图8 关节角1参考轨迹跟踪仿真结果Fig.8 Simulation results of joint angle 1 in trajectory tracking experiments
由上图可知滑模控制在跟踪正弦轨迹时响应速度很快,在0.21 s时误差即在2%。控制力矩在初始时刻较大,随着实际关节轨迹趋近于期望关节轨迹,控制力矩将趋于0。
通过该仿真试验可知该控制律控制精度满足控制要求,下面完成实物试验。
在WAM机械臂的Ubuntu12.04实时操作系统上用C++编写控制程序实现上述控制算法。由PC机通过Socket协议向机械臂发出控制指令,从而实现对机械臂的实时控制。本试验用于跟踪一个参考轨迹θd(t),其表达式为:θ (t)
d初始条件为θ(0) = [0.1 - 0.6854 0.1 1.6708]T, 控制律的相关参数设为 λ = 70Ι4×4、Κ = 50Ι4×4、ε= [0.5 0.5 0.5 0.5]T。 得到如图9所示结果。
由多关节联动试验可知,滑模控制可以对多关节同时进行高精度跟踪。
4.4 避障抓取试验
如图10~11所示,在完成目标识别与定位后,通过期望轨迹计算得到有效关节轨迹,控制机械臂跟踪该路径,同时还需要避免各关节与障碍物的碰撞,在空间足够的地方,张开Bhand⁃280机械手,然后在接近目标的位置处实施抓取动作。在目标位置完成抓取后,机械臂需要收回到基座,这时同样需要避免各关节与障碍物的碰撞。最终的抓取试验是成功的。
5 结论
本文通过仿真验证及实物抓取验证,实现了基于深度学习的的目标快速精确识别,能在小样本环境下快速给出目标的分类及定位信息,为抓取规划控制提供了前提。同时从实际机械臂运行精度可以得出所设计滑模控制律具有使用可靠性。但目前实验环境相对单一,验证任务相对简单,后续将在本文的基础上在高动态环境下复杂多目标识别,协同抓取等方面展开进一步研究。

图10 机械臂避障抓取目标过程Fig.10 The process of obstacle avoidance and target capture by the robotic arm

图11 机械臂抓取目标后返回避障过程Fig.11 The process of obstacle avoidance and retur⁃ning after target grasping of the robotic arm
[1] 邓桦.机械臂空间目标视觉抓取的研究[D].哈尔滨:哈尔滨工业大学,2013.
Deng Hua.Research on Visual Capture of Robot Arm with Spatial Target[D].Harbin: Harbin Institute of Technology,2013.(in Chinese)
[2] 于灏洋.基于双目视觉的伺服机械臂运动控制研究[D].大连:大连理工大学,2016.
Yu Haoyang.Research on Motion Control of Servo Arm based on Binocular Vision [D].Dalian: Dalian University of Tech⁃nology, 2016.(in Chinese)
[ 3 ] Redmon J, Divvala S, Girshick R, et al.You only look once: Unified, real⁃time object detection[C] //Proceedings of the IEEE Conference on Computer Vision and Pattern Rec⁃ognition.2016: 779⁃788.
[ 4 ] Redmon J, Farhadi A.YOLO9000: better, faster, stronger[J].arXiv preprint arXiv: 1612.08242, 2016.
[5] The WAMTMArm [EB/OL].https://www.barrett.com/wam⁃arm/.
[6] 孟韶南,梁雁冰,师恒.基于ROS平台的六自由度机械臂运动规划[J].上海交通大学学报, 2016(S1):94⁃97.
Meng Shaonan, Liang Yanbing, Shi Heng.Motion planning of six degree of freedom robot arm based on ROSplatform[J].Journal of Shanghai Jiao Tong University, 2016(S1): 94⁃97.(in Chinese)
[7] 刘鹏,王强,张伟.机械臂动力学建模及控制仿真[J].自动化与仪表, 2017(03): 9⁃12.
