Testing and evaluation for fatigue crack propagation of Ti-6Al-4V/ELI and 7050-T7452 alloys at high temperatures

Yunto ZHU,Junjing XIONG,*,Zhiyng LV,Yngung ZHAO

aSchool of Transportation Science and Engineering,Beihang University,Beijing 100083,China

bAECC Beijing Institute of Aeronautical Materials,Beijing 100095,China

1.Introduction

Because of their superior stiffness and strength,excellent resistance to creep,oxidation and corrosion,and good fracture toughness at high temperature,advanced metallic alloys(e.g.,titanium and aluminium alloys,Ni-based singlecrystalline or polycrystalline superalloys,etc.)are widely used in advanced aircraft and aero-engines as airframe component and gas turbine blade materials,where they commonly encounter a wide range of temperature(25–1000 °C).High temperatures can strongly affect the fatigue properties and damage mechanism.With the increasing temperature,some metallic alloys considerably undergo the decrease in fatigue strength(e.g.,low-cycle fatigue resistance1,2and high-cycle fatigue strength3,4)and in fracture resistance(e.g.,fracture threshold5–7and fracture toughness8),but the increase in crack growth rates,9–16ultimately decreasing fatigue life.The reason for this is that fatigue crack initiation and propagation of metallic materials at high temperature is a progressive damage process with the synergistic interaction between fatigue,creep and oxidation under thermo-mechanical stresses,and some metallic alloys suffer from a fatigue transition mechanism from brittle cleavage fracture at lower temperatures to ductile quasicleavage fracture at higher temperatures,and a plasticity induced and oxide induced crack closure mechanism.A significant body of research exists covering quantitative models for depicting the fatigue properties of low-cycle ε-N1,2and highcycle S-N,3,4fracture threshold6and fracture toughness,8and crack propagation rate6,9,11–14at high temperatures.In addition,a number of models accounting for the fatiguecreep-oxidation interaction have been proposed to express crack propagation behavior at high temperature by using the linear summation rule.17–20Based on the linear elastic fracture mechanics(LEFM), finite element(FE)modelling for crack propagation behavior and residual life at high temperature are also covered in several works.21,22As a result,fully understanding the effects of high temperatures on the fatigue properties and damage mechanism of metallic alloys at high temperatures is becoming increasingly important for assessing failure limits and reliability during the design prediction stage of advanced aircraft and gas turbine engines.

During actual operation of aircraft or steam turbine engines,many metallic alloy components often undergo variableamplitude rather than constant-amplitude loading histories,and the effects of load interaction have an appreciable influence on fatigue life in the environment of high temperature.23Therefore,high temperature fatigue under variable amplitude loading histories is the single most common cause of failures of aircraft or gas turbine engines.Although a large amount of research has been conducted on the fatigue and fracture properties and lives of alloy steels and superalloys at high temperatures,the effect of high temperature on the crack growth properties of Ti-6Al-4V/ELI and 7050-T7452 has been scarcely reported,and the load interaction on the residual lives of the aforementioned alloys subjected to variable amplitude loading histories at high temperature has not been systematically studied.Because of their superior mechanical properties at high temperatures,Ti-6Al-4V/ELI and 7050-T7452 have been widely used in advanced aircraft and gas turbine engines as airframe or rotor spindle materials,where they commonly experience random-spectra loading histories in a high temperature environment.The random-spectra loading can cause crack initiation and propagation from small defects in airframes.Hence,a need exists for fully understanding the effect of high temperature on the crack growth properties of Ti-6Al-4V/ELI and 7050-T7452;furthermore,a technique for assessing the load interaction effect in engineering design for advanced aircraft or gas turbine engines is desirable,which is the focus of this paper.

2.Experiments

2.1.Experimental methodology

All M(T)(or middle tension)specimens for fatigue tests were manufacturedfrom Ti-6Al-4V/ELIor7050-T7452.The mechanical properties of material are listed in Table 1(here σsis the yield ultimate strength and r is the overload shut-off ratio),and the geometry and dimensions of the specimens are shown in Fig.1.All specimens have an initial artificial prefabricated crack size of 8 mm through linear cutting and polishing.All fatigue tests were conducted on a MTS-880-100 kN servo-hydraulic machine under axial cyclic loadingswith a sinusoidal waveform at a loading frequency of 10 Hz in room environment(shown in Fig.2(a)).During tests,a WZHD0850 long focal-length optical telemicroscope with measurement accuracy within 0.01 mm was utilized to measure the crack sizes at a specific interval of cyclic loading until the rupture of specimen.Notably,the crack growth tests on M(T)specimen always necessitate two long focal-length optical telemicroscopes to separately measure four crack lengths at the left and right sides on the front and back surfaces of specimen,and the mean value of four crack lengths is regarded as the actual crack length.However,due to resource constraint and measuring difficulty,from an engineering viewpoint,the M(T)specimens were thought to be thin enough,and the crack lengths at the left and right sides on the front surface of specimen are as same as those on the back surface.Therefore,in this work,only two crack lengths at the left and right sides on the front surface of specimen were measured at a specific interval of cyclic loading until the rupture of specimen,by using a long focal-length optical telemicroscope,and the mean value was argued to be defined as the actual crack length.In addition,a SDGDYD-180/+350 environmental chamber whose temperature fluctuated within ±2°C was employed to maintain the testing temperatures of 250 °C and 150 °C through controlling the electromechanical heater of environmental chamber.A pre-crack of about 2.0 mm length was made along both left and right notch-edge cracks on all specimens at the beginning of tests.

Table 1 Material properties for both alloys.

Fig.1 Geometry and dimensions of M(T)specimen for fatigue crack growth tests.

It is noteworthy that due to the great size of hydraulic grip system,it is hard to install the hydraulic grip system in environmental chamber,and the mechanical fixtures were then used to grip the M(T)specimen(shown in Fig.2(b)and(c)).From Fig.2(b)and(c),it is clear that four fastening holes and one centering hole were manufactured on the mechanical fixture,and the M(T)specimen was first fixed on the mechanical fixtures through the centering rods,and then gripped and clamped by tightening the bolts.In order to make sufficient clamping and friction forces on the M(T)specimen for transferring the tension-compression loading,the circular arc grooves were fabricated at the root of grip fixture to reduce the stiffness of grip for increasing the clamping force,and the knurling grip surfaces were manufactured to increase the roughness for increasing the friction factor(shown in Fig.2(c)).For these reasons,we argue that the mechanical fixtures transfer the axial loading by sufficiently clamping and friction forces on the M(T)specimen,but not by pin-loading.

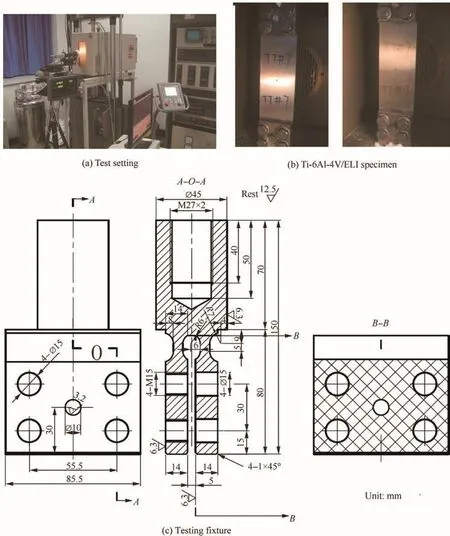
Fig.2 High temperature fatigue crack growth measurement.

Four categories of crack growth tests were prepared.Two of them were constant-amplitude loading tests at room temperature of about 25 °C and at high temperature of 250 °C or 150°C to determine pure and high temperature crack growth properties,separately.Two other categories were actual random-spectra loading tests at about 25 °C and at 250 °C or 150°C to obtain pure and high temperature residual lives,respectively.The high temperatures of 250 °C and 150 °C represent the maximum operation temperatures to which Ti-6Al-4V/ELI and 7050-T7452 are commonly subjected in airframe applications,respectively.Furthermore,three stress ratios of-1,0.06 and 0.5 were implemented for the tests of constantamplitude loading,and at least three specimens were utilized for each stress ratio.Meanwhile,two reference stress levels of 176.0 MPa and 66.7 MPa were employed for the tests of actual random-spectra loading on Ti-6Al-4V/ELI and 7050-T7452,separately,and at least three specimens were used for each reference stress level.Note that two reference stress levels of 176.0 MPa and 66.7 MPa represent the common working stress levels on Ti-6Al-4V/ELI and 7050-T7452 in an airframe,respectively.

Fig.3(a)and(b)show the sequences and the coefficient values of 1000 and 116884 load peaks and valleys(i.e.,500 and 58442 load cycles)in a block of actual random-spectra loading history for Ti-6Al-4V/ELI and 7050-T7452,respectively.n is the number of fatigue loads in Fig.3(a)and(b).Table 2 also shows the reference stress levels for the two materials.Notably,the reference stress levels in Table 2 and the load coefficient in Fig.3(a)and(b)are not the actually applied load levels for the two materials.The actually applied load levels for the two materials should be determined by multiplying the reference stress levels in Table 2 by the load coefficients in Fig.3(a)and(b),separately.As a result,two actually applied random-spectra loading histories for Ti-6Al-4V/ELI and 7050-T7452 can be obtained by multiplying the reference stress levels of 176.0 MPa and 66.7 MPa in Table 2 by the load coefficients in Fig.3(a)and(b),respectively.

Fig.3 Actual random-spectra load histories for Ti-6Al-4V/ELI and 7050-T7452.

Table 2 Residual lives for both alloys under random-spectra loading.

It is worth noting that the crack length was defined as the half of the corresponding full crack length during all tests,and an initial crack size a0of about 2 mm was pre-cracked through cyclic loading at the beginning of all tests.

2.2.Experimental results and discussion

Through constant-amplitude loading tests,the experimental data-sets of crack length ai(i.e.,halves of the corresponding full crack lengths)versus number of stress cycles Niwere determined and the crack growth rates （da/dN）icorresponding to the crack length aiwere calculated based on the secant method25from an experimental dataset[ai,Ni].In accordance with standards ASTM E647-15,25the stress intensity range for the M(T)specimen is

where α is the corrected coefficient for crack size in the plain plate with finite width and α=2a/W,where a is the crack size or length;W is the width of specimen;B is the thickness of specimen;ΔP is the load range.

By means of Eq.(1),the stress intensity range （ΔK）icorresponding to the crack length aiwere also calculated and an experimental dataset[（da/dN）i,（ΔK）i]was then obtained.

The experimental datasets under constant-amplitude loading at about 25 °C,250 °C and 150 °C are shown in Fig.4(here R is the stress ratio and T is the temperature).The results in Fig.4 lead to the following deductions:

(i)The crack growth rates for both alloys in both temperature environments increase with the increasing stress ratio.The reason for this is that lower stress ratio is more likely to induce the closure of fracture faces at crack tip and to decrease crack growth rates.These results are consistent with the research closures of previous works.26,27

(ii)In the same stress ratio case,the crack growth rates of 7050-T7452 are much greater at 150 °C than at 25 °C.This is probably due to the reduction in Young’s modulus and yield strength of 7050-T7452 at high temperature,which leads to a severer plastic deformation at crack tip and an increase in crack growth rates.However,there is insignificant difference between the crack growth rates of Ti-6Al-4V/ELI at 250 °C and at 25 °C,and in particular,the crack growth rates of Ti-6Al-4V/ELI at stress ratio of 0.5 are slightly less at 250°C than at 25°C.This likely owes to the nucleation and growth of secondary cracks,and the oxide-induced and roughness-induced crack closure effects at higher temperature.In reality,at higher temperature,the nucleation and growth of secondary cracks lead to an increase in the roughness of fracture surfaces and a reduction in crack driving force.Moreover,the oxideinduced and roughness-induced crack closure effects decrease the effective stress intensity range.The efforts in this paper have a good agreement with those in literatures.28–31Hereby,we propose that the crack growth rate behavior of Ti-6Al-4V/ELI is unsusceptible to the high temperature,but that of 7050-T7452 is susceptible.High temperature substantially and adversely affects the crack growth behavior of 7050-T7452,but slightly and even beneficially influences the crack growth rate of Ti-6Al-4V/ELI.

Fig.4 Crack growth behavior of da/dN-ΔK curve for Ti-6Al-4V/ELI and 7050-T7452.

The experimental results under actual random-spectra loading are shown in Table 2.The results in Table 2 result in the following deductions:

At the same reference stress level,the mean value of crack growth life for Ti-6Al-4V/ELI is 15.2%greater at 250°C than at 25 °C(here ［（603-511.4）/603］× 100%=15.2%),whereas that for 7050-T7452 is 35.8%less at 150 °C than at 25 °C(here［（4.36-2.8）/4.36］× 100%=35.8%).It is noteworthy to point out that from the rain- flow counting analysis of actual random-spectra loading history,a substantial amount of load cycles with the stress ratios within a range from 0.06 to 0.5 exist in actual random-spectra loading history,and fatigue crack growth rates of Ti-6Al-4V/ELI corresponding to these load cycles at high temperature are close to those at room temperature.However,there are also a large number of load cycles with the negative stress ratios in actual random-spectra loading history,and fatigue crack growth rates of Ti-6Al-4V/ELI pertinent to these load cycles at high temperature are different from those at room temperature(see Fig.4(a)).This result leads to 13.4%greater crack growth life for Ti-6Al-4V/ELI subjected to actual random-spectra loading history at high temperature than at room temperature.

2.3.Fractographic analysis

To understand the damage mode and mechanism,and the differences between the damage modes and mechanisms for both alloys at room temperature and at high temperature,representative fracture surfaces of failed specimens were analyzed fractographically using a scanning electron microscope(SEM)to provide direct evidence of crack growth in regions unobservable during the fatigue process.The fracture surfaces of both alloys are shown in Figs.5–7.Note that by using Eq.(1),the ranges of stress intensity factor ΔK in Figs.5 and 6 were determined from the crack length a corresponding to fractographic picture provided by SEM and the constant amplitude fatigue load ΔP.

Significant results that emerged from the fractographic analysis are summarized as follows:

(i)Figs.5 and 6 clearly show serial and fine plastic fatigue striations,which demonstrates a smooth and stable crack growth under constant-amplitude loading,while Fig.7 exhibits sparse and discrete plastic fatigue striations and abundant ductile dimples between fatigue striations,which illustrates a significant load-interaction effect arising from the random-spectra loading,in other words,the load variations within actual random-spectra load history contribute to the alternation between a smooth and stable crack growth and an instantaneous sharp separation of the dimple at crack tip.The clear plastic fatigue striations appear on fracture surfaces of both alloys,which indicates the occurrence of local plastic deformation at crack tip at room and high temperatures.

(ii)Fig.5(a),(c)and(e)evidently display extensive cleavage steps and tearing ridges for 7050-T7452.In contrast,Fig.5(b),(d)and(f)reveal the plastic fatigue striations,oxidation productions,ductile equal-axis dimples,voids and second-phase particles,and tearing ridges for 7050-T7452.Therefore,fatigue failure modes for 7050-T7452 under constant-amplitude loading can be considered as the mixed brittle cleavage and ductile quasi-cleavage fracture at room temperature,but the ductile quasicleavage fracture at high temperature.Furthermore,abundant oxidation productions can weaken the grain boundary binding and it is easier for micro pore and defect to initiate along grain boundary,drastically increasing fatigue crack growth.Consequently,high temperature substantially and adversely affects the crack growth behavior.

Fig.5 Fractographic pictures for 7050-T7452 under constant-amplitude loading.

(iii)Fig.6(a),(c)and(e)clearly expose substantial cleavage steps and fracture facets on fracture surfaces of Ti-6Al-4V/ELI subjected to constant-amplitude loading at room temperature,whereas Fig.6(b),(d)and(f)demonstrate the plastic fatigue striations,oxidation productions and secondary cracks on fracture surfaces for Ti-6Al-4V/ELI subjected to constant-amplitude loading at high temperature.Thus,fatigue failure modes for Ti-6Al-4V/ELI under constant-amplitude loading can be concluded as the brittle cleavage fracture at room temperature,but the mixed brittle cleavage and ductile quasi-cleavage fracture at high temperature.As mentioned in the previous fractographic analysis result(ii),high temperature substantially and adversely affects the crack growth behavior;however,the initiation and propagation for substantial secondary cracks on fracture surfaces of Ti-6Al-4V/ELI at high temperature can dissipate and disperse the energy to drive crack growth,and release localized stress concentration at the tip of crack,considerably decreasing fatigue crack growth.Thereby,we propose that the initiation and propagation of secondary crack is the primary reason for a slight influence of high temperature on the crack growth behavior of Ti-6Al-4V/ELI.

(iv)Figs.5(b),(d),(f)and 6(b),(d),(f)also show more intense oxidation productions on fracture surfaces of both alloys subjected to constant-amplitude loading in high temperature environments at negative stress ratio of-1 than at two positive stress ratios of 0.5 and 0.06.Consequently,we deduce that the cyclic loading mode(i.e.,positive or negative stress ratio)considerably influences the crack growth properties of both alloys at high temperatures,namely,the negative stress ratio has a more detrimental effect on the crack growth properties of both alloys at high temperatures than the positive stress ratio.

Fig.6 Fractographic pictures for Ti-6Al-4V/ELI under constant-amplitude loading.

3.Evaluating crack growth behavior and residual life

3.1.Depicting temperature-dependent crack growth behavior

A three-parameter empirical power function formula is commonly used to characterize materials’crack growth properties as32

where N is the number of stress cycle,da/dN is the crack growth per stress cycle,R is the stress ratio,C is the crack propagation resistance coefficient,m1and m2are the material constants or crack propagation exponents,and ΔK0is the fracture threshold fitted from experimental data.

Note that(i)the crack propagation resistance coefficient C is an important material property to characterize fatigue crack propagation for constant-amplitude loading(i.e.,the greater the crack propagation resistance coefficient C is,the faster the crack growth rate becomes),and is dependent on the material properties,the material thickness,the orientation of the crack relative to principal material directions and the loading environment.33,34(ii)The fracture threshold ΔK0in Eq.(2)is not really the fatigue crack growth threshold value ΔKthof given materials.Actually,the fracture threshold ΔK0in Eq.(2)is the idealized material property corresponding to near zero crack growth rate,obtained by a regression process of crack growth rate vs.ΔK data in Paris region,in a threedimensional logarithmic coordinate system.The introduction of fracture threshold ΔK0has helped Eq.(2)with better fitting precision.

Eq.(2)is a da/dN-ΔK-R surface equation to express the relationship between the stress intensity range ΔK,stress ratio R and fatigue crack growth rate da/dN in a three dimensional coordinate system.The undetermined material constants C,m1,m2and ΔK0in Eq.(2)can be determined by best fitting from experimental datasets.By means of Eq.(2),the da/dN- ΔK-R surfaces for both alloys at 25°C,250 °C and 150 °C were determined from the experimental datasets in Fig.4(a)and(b).Table 3 shows the results of the da/dN-ΔK-R surfaces.The da/dN-ΔK curves for both alloys were deduced from the da/dN-ΔK-R surface models in Table 3.The da/dN-ΔK-R surfaces(shown in Table 3)are plotted in Fig.8(a)and(b),and the da/dN-ΔK curves are plotted in Fig.4(a)and(b).

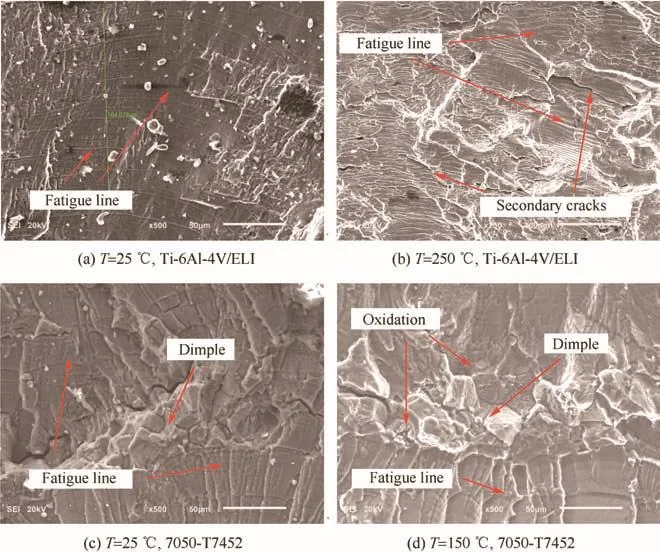
Fig.7 Fractographic pictures for both alloys under random-spectra loading.

Table 3 Crack growth rate da/dN-ΔK-R surfaces.

Fig.8 Crack growth rate da/dN-ΔK-R surfaces for Ti-6Al-4V/ELI and 7050-T7452.

From Table 3 and Figs.4(a),(b)and 8(a),(b),it is obvious that(i)good agreement is achieved between the experimentaldata and the predicted surface;(ii)the crack propagation resistance coefficient C for Ti-6Al-4V/ELI at 250°C obtained by best fitting of the model is close to that at 25°C.Conversely,that for 7050-T7452 is much greater at 150 °C than at 25 °C;(iii)the da/dN-ΔK-R surfaces for Ti-6Al-4V/ELI at 250 °C and at 25 °C are close to(even intersect)each other,but that for 7050-T7452 is upper at 150 °C than at 25 °C,which indicates that high temperature has an insignificant influence on the crack propagation behavior of Ti-6Al-4V/ELI,but a significant adverse effect on the crack propagation behavior of 7050-T7452;(iv)fatigue crack growth rates for both alloys depicted by the surface model Eq.(2)increase with the increasing stress ratio and stress intensity range,respectively;(v)the differences between da/dN-ΔK-R surfaces for both alloys at both temperatures decrease with the increasing stress ratio and stress intensity range,respectively.Thus,we propose that the surface model Eq.(2)has adequately and logically characterized the physical characteristics and the phenomenological quantitative laws of crack growth behavior.Importantly,the parameters of this model can be determined expediently and easily.

Table 4 Walker model for crack growth rate.

Notably,if the effect of fracture threshold ΔK0is neglected,then Eq.(2)can be degraded into the Walker model35:

In general,the Walker model Eq.(3)is used to depict fatigue crack growth rate da/dN at both positive and negative ratios,in other words,the parameters of the Walker model Eq.(3)are determined from the crack growth rate data at positive and negative ratios by fitting,respectively.By means of Eq.(3),the Walker models for both alloys at 25 °C,250 °C and 150°C were determined from the experimental datasets in Fig.4(a)and(b)respectively.Table 4 shows the results of Walker model.

3.2.Estimating temperature-dependent residual life

The Willenborg-Chang model based on plastic zone theory has been proved to be successful in modelling the load interaction on residual life under random-spectra loading by introducing the effective stress ratio Reffat crack tip.24Therefore,incorporating the Willenborg-Chang model and the da/dN-ΔK-R surface model with three parameters(i.e.,Eq.(2)),it is possible to predict the crack growth increment for the ith stress cycle in a block of random-spectra load history as follows.

otherwise,

where Reffis the effective stress ratio,（Kmax）effis the effective maximum nominal stress intensity, （Kmax）this the maximum nominal stress fracture threshold, （Kmax）OLis the overload maximum nominal stress intensity,ZOLis the size of overload plastic zone,and Δa′is the increment of crack growth through the overload plastic zone.

From Eqs.(4)–(9)and material properties listed in Table 1,and actual random-spectra load history,with cycle-by-cycle accumulation damage calculation,all crack growth increments pertaining to each subsequent adjacent stress cycle in actual random-spectra load history can be calculated until final failure,and the cumulative number of stress cycle(i.e.,residual life or crack growth life)corresponding to each current crack size can be obtained and recorded.Thus,the residual life pertinent to final crack size is modelled based on the aforementioned modified damage accumulation rule,incorporating the Willenborg-Chang model and the da/dN-ΔK-R surface model.Apparently,the load interaction under actual random-spectra loading is taken into account in residual life prediction through the aforementioned modified damage accumulation rule.

Similarly,incorporating the Willenborg-Chang model and the Walker model,the crack growth increment for the ith stress cycle in a block of random-spectra load history can also be calculated as

Using the aforementioned modified damage accumulation rules,the residual lives for Ti-6Al-4V/ELI and 7050-T7452 are calculated from actual random-spectra load histories shown in Fig.3(a)and(b),the material properties listed in Table1,theda/dN-ΔK-R surface models listed in Table 3 and the Walker models listed in Table 4.During the prediction of residual lives,the consistent initial crack length a0is chosen to be the initial pre-cracked size of 2 mm under cyclic loading at the beginning of all tests,as mentioned at the end of Section 2.1.The calculated results are listed in Table 2.

The results in Table 2 lead to the following deductions:(i)for the Walker model,the maximum relative deviations of residual life predictions for Ti-6Al-4V/ELI and 7050-T7452 from experiments are 23.7%and 47.0%respectively;(ii)for the da/dN-ΔK-R surface model,the maximum relative deviations of residual life predictions for Ti-6Al-4V/ELI and 7050-T7452 from experiments are 21.8%and 23.9%respectively,with the acceptable scatter.Namely,the residual life predictions based on the da/dN-ΔK-R surface model are closer to the experimental results than those from the Walker model;(iii)one reason for the larger deviations of the predicted results of the Walker model from the experimental data than those of the da/dN-ΔK-R surface model is the neglect of the effect of fracture threshold.In reality,there are a large number of small load cycles in actual random-spectra loading history for Ti-6Al-4V/ELI and 7050-T7452,which can cause lower stress intensity factor ranges than the fracture threshold.Thus,it is argued that the modified damage accumulation rule from the da/dN-ΔK-R surface model can provide a reasonable prediction for temperature-dependent residual life of metallic alloys.

4.Conclusions

The focus of this paper is to evaluate crack propagation behaviors and residual lives of metallic alloys subjected to fatigue loading at room and high temperatures.Fatigue tests were performed on Ti-6Al-4V/ELI and 7050-T7452 subjected to constant-amplitude and random-spectra loading histories at 25 °C and at 250 °C and 150 °C.The damage mode and mechanisms at high temperature were compared with those at room temperature on the basis of the results of fractographic analysis.Temperature-dependent residual lives under actual random-spectra loading were evaluated based on a modified accumulation damage rule.The underpinning work contains three features:

(i)Fatigue failure modes for 7050-T7452 under constantamplitude loading can be considered as the mixed brittle cleavage and ductile quasi-cleavage fracture at room temperature,but the ductile quasi-cleavage fracture at high temperature.Conversely,fatigue failure modes for Ti-6Al-4V/ELI under constant-amplitude loading can be concluded as the brittle cleavage fracture at room temperature,but the mixed brittle cleavage and ductile quasi-cleavage fracture at high temperature.

(ii)The crack growth rate behavior of Ti-6Al-4V/ELI is unsusceptible to the high temperature,but that of 7050-T7452 is susceptible.High temperature substantially and adversely affects the crack growth behavior of 7050-T7452,but slightly influences the crack growth behavior of Ti-6Al-4V/ELI.The initiation and propagation of substantial secondary cracks is the primary reason for a slight influence of high temperature on the crack growth behavior of Ti-6Al-4V/ELI.

(iii)A modified accumulation damage rule,accounting for the load interaction, is presented to predict temperature-dependent residual lives of both alloys subjected to actual random-spectra load history.Good correlation is achieved between the predictions from the modified ruleproposed in thepaperand actual experiments.

It is worth noting that the conclusions on the crack growth behavior for Ti-6Al-4V/ELI and 7050-T7452 are valid only for the temperatures used in the test,or 250 °C and 150 °C.

Acknowledgements

This project was supported by the National Natural Science Foundation of China(No.51375033).

1.Chu ZK,Yu JJ,Sun XF,Guan HR,Hu ZQ.High temperature low cycle fatigue behavior of a directionally solidified Ni-base superalloy DZ951.Mater Sci Eng A 2008;488(1–2):389–97.

2.Fan KL,Liu XS,He GQ,Chen H.Elevated temperature low cycle fatigue of a gravity casting Al-Si-Cu alloy used for engine cylinder heads.Mater Sci Eng A 2015;632:127–36.

3.Liu Y,Yu JJ,Xu Y,Sun XF,Guan HR,Hu ZQ.High cycle fatigue behavior of a single crystal superalloy at elevated temperatures.Mater Sci Eng A 2007;454:357–66.

4.Qiu CL,Wu XH.High cycle fatigue and fracture behavior of a hot isostatically pressed nickel-based superalloy.Phil Mag 2014;94(3):242–64.

5.Shyam A,Padula SA,Marras SI,Milligan WW.Fatigue-crackpropagation thresholds in a nickel-base superalloy at high frequencies and temperatures.Metall Mater Trans A 2002;33(7):1949–62.

6.Ding J,Hall R,Byrne J.Effects of stress ratio and temperature on fatigue crack growth in a Ti-6Al-4V alloy.Int J Fatigue 2005;27(10–12):1551–8.

7.Zhang M,Song XP,Yu L,Li HL,Jiao ZH,Yu HC.Fatigue small crack growth threshold determination of a high-Nb TiAl alloy at different temperatures by in-situ observation.Int J Miner Metall Mater 2013;20(12):1192–7.

8.Tanaka K,Amita T,Satou T,Koba K,Kusumoto J,Kanaya A.Evaluation on high temperature fracture toughness of CrMoV cast steel by small punch testing.Int J Press Vessel Pip 2009;86(9):643–8.

9.Zhu SJ,Peng LM,Moriya T,Mutoh Y.Effect of stress ratio on fatigue crack growth in TiAl intermetallics at room and elevated temperatures.Mater Sci Eng A 2000;290(1–2):198–206.

10.Hsu KC,Lin CK.High temperature fatigue crack growth behavior of 17–4 PH stainless steels.Metall Mater Trans A 2004;35(9):3018–24.

11.Andersson M,Persson C,Melin S.High temperature fatigue crack growth in Inconel 718 subjected to high strain amplitudes.Fatigue Fract Eng Mater Struct 2006;29(11):863–75.

12.Yamamoto M,Kitamura T.Effect of microstructure on crack propagation in high temperature fatigue of directionally solidified Ni-based superalloy.Fatigue Fract Eng Mater Struct 2006;29(6):431–9.

13.Zhong ZH,Gu YF,Yuan Y,Cui CY,Yokokawa T,Harada H.Fatigue crack growth behavior of a newly developed Ni–Co-base superalloy TMW-2 at elevated temperatures.Mater Sci Eng A 2012;552(34):464–71.

14.Wang L,Huang X,Guo G,Hu Y,Zhang L.Fatigue crack propagation behavior of a nickel based super alloy at elevated temperatures.Mater Res Innov 2014;18(S4):1087–90.

15.Kuhn F,Zeismann F,Brueckner-Foit A.Crack growth mechanisms in an aged superalloy at high temperature.Int J Fatigue 2014;65:86–92.

16.Adair BS,Johnson WS,Antolovich SD,Staroselsky A.Crystallographic orientation and temperature effects on the fatigue crack growth rate and resulting fracture surface morphology in PWA1484 single crystal superalloy.Eng Mater Struct 2015;38(1):56–68.

17.Martinez-Esnaola JM,Martin-Meizoso A,Affeldt EE,Bennett A,Fuentes M.High temperature fatigue in single crystal superalloys.Fatigue Fract Eng Mater Struct 1997;20(5):771–88.

18.Ruiz-Sabariego JA,Pommier S.Oxidation assisted fatigue crack growth under complex non-isothermal loading conditions in a nickel base superalloy.Int J Fatigue 2009;31(11–12):1724–32.

19.Bouvard JL,Gallerneau F,Paulmier P,Chaboche JL.A phenomenological model to predict the crack growth in single crystal superalloys at high temperature. Int J Fatigue 2012;38:130–43.

20.Barker VM,Johnson WS,Adair BS,Antolovich SD,Staroselsky A.Load and temperature interaction modeling of fatigue crack growth in a Ni-base superalloy.Int J Fatigue 2013;52:95–105.

21.Ismonov S,Loghin A,Hanlon T,Shen C.Application of crack tip plasticity based fatigue modelon high temperature alloy HAYNES(R)282(R).Int J Fatigue 2015;70:146–53.

22.Jovicic G,Nikolic R,Zivkovic M,Milovanovic D,Jovicic N,Maksimovic S,et al.An estimation of the high pressure pipe residual life.Arch Civ Mech Eng 2013;13:36–44.

23.Zakaria KA,Abdullah S,Ghazali MJ,Azhari CH.Influence of spectrum loading sequences on fatigue life in a high temperature environment.Eng Fail Anal 2013;30:111–3.

24.Chang JB,Szamossi M,Liu KW.Random spectrum fatigue crack life predictions with or without considering load interactions.In:Chang JB,Hudson CM,editors.Methods and models for predicting fatigue crack growth under random loading.Philadelphia:ASTM;1981.p.115–32.

25.American Society for Testing and Materials.Standard test method for measurement of fatigue crack growth rates.Report No.:ASTM E647-15;2015.

26.Riddell WT,Piascik RS.Stress ratio effects on crack opening loads and crack growth rates in aluminum alloy 2024.In:Panontin SD,Sheppard SD,editors.Fatigue and fracture mechanics:twentyninth volume.West Conshohocken:ASTM;1999.p.407–25.

27.Boyce BL,Ritchie RO.Effect of load ratio and maximum stress intensity on the fatigue threshold in Ti–6Al–4V.Eng Fract Mech 2001;68(2):129–47.

28.Arakere NK,Goswami T.High temperature fatigue crack growth behavior of Ti-6Al-4V.High Temp Mater Process 2002;21(4):229–36.

29.Ogawa T,Hayashi Y,Tokaji K,Hirose M.Fatigue crack growth of Ti-6Al-4V alloy at elevated temperatures.J Soc Mater Sci Japan 1993;42(481):1186–92.

30.Prasad K,Abhaya S,Amarendra G,Kumar V,Rajulapati KV,Bhanu Sankara Rao K.Fatigue crack growth behavior of a near α titanium alloy Timetal 834 at 450 °C and 600 °C.Eng Fract Mech 2013;102:194–206.

31.Mercer C,Lou J,Allameh SM,Soboyejo WO.Effects of temperature on the fatigue crack growth behavior of cast gamma-based titanium aluminides.Metall Mater Trans A 2001;32(11):2781–94.

32.Wang CQ,Xiong JJ,Shenoi RA,Liu MD,Liu JZ.A modified model to depict corrosion fatigue crack growth behavior for evaluating residual lives of aluminium alloys.Int J Fatigue 2016;83:280–7.

33.Wang R.A fracture model of corrosion fatigue crack propagation of aluminum alloys based on the material elements fracture ahead of a crack tip.Int J Fatigue 2008;30(8):1376–86.

34.Wang R,Zheng X.Corrosion fatigue crack propagation of an aluminum alloy under periodic overloads.Fatigue Fract Eng Mater Struct 2012;35(5):389–98.

35.Walker EK.The effect of stress ratio during crack propagation and fatigue for 2024–T3 and 7075–T6 aluminum Effects of environment and complex load history on fatigue life.Philadelphia:ASTM;1968.p.1–14.