A multi-order method for predicting stability of a multi-delay milling system considering helix angle and run-out effects

Shanglei JIANG,Yuwen SUN

Key Laboratory for Precision and Non-Traditional Machining Technology of the Ministry of Education,Dalian University of Technology,Dalian 116024,China

1.Introduction

Milling operations are widely used in the aerospace industry for machining various highly expensive components,such as aero-engine blisks,impellers,blades,casings,and so on.These components are mostly made of aluminum alloys,or difficult-to-cut titanium and nickel alloys.In the milling process,chatter is an undesirable phenomenon that inevitably deteriorates workpiece quality and even causes damages to CNC machine tools.1How to avoid chatter is a key issue to ensure a stable cut with a high material removal rate.Chatter stability prediction plays an important role in selecting machining parameters in order to achieve a chatter-free operation.Generally,it utilizes stability lobes to classify machining parameter combinations into stable and unstable regions in a diagram,2namely the stability lobe diagram(SLD).An optimal cutting parameter combination chosen in a stable region not only avoids chatter,but also improves machining productivity.Therefore,it is particularly necessary and important to seek an effective prediction method.

Apart from the trial and error method,some feasible methods including analytical and numerical methods have been proposed in the frequency domain and the discrete time domain.Altintas and Budak3proposed the first analytical solution in the frequency domain.Their method,known as the single-frequency solution(SFS),can give a rapid and accurate computation of the SLD in a large radial immersion case.In order to improve the prediction accuracy in a small radial immersion case,a multi-frequency solution(MFS)was further proposed by Budak and Altintas4,which uses the higher harmonics of directional factors instead of the average ones used in the SFS.Alternately,based on the Floquet theory of delaydifferential equations(DDEs),modeling in the discrete time domain is also a good choice to achieve accurate stability predictions.Bayly et al.5solved discrete time equations by using temporal finite elements analysis to determine stability boundaries.Butcher et al.6proposed the Chebyshev collocation method in the discrete time domain to predict the stability of a time-periodic DDE.Both methods use one matrix to construct the Floquet transition matrix(FTM)in a similar way,and they are very competitive for their rates of convergence.However,they are only easy to use for single-delay cases and not quite suitable for cases with varying or multiple time delays.

On the other hand,Insperger and Stépán7investigated the periodic motion of time-period DDEs using the semidiscretization(SD)method,in which only the delay term and the periodic coefficient term are discretized.An updated version of the SD method8,known as the zeroth-order SD(0th SD)method,was then applied to predict the stability of milling processes,in which the delay term was discretized as a weighted sum of two neighboring discrete state values.Furthermore,a first-order SD(1st SD)method9was developed to essentially increase the efficiency of the original SD method,in which the delay term was then approximated by linear interpolation of two neighboring discrete state values.Alternatively,Ding et al.10proposed a first-order full-discretization(1st FD)method with a faster computational efficiency.In addition to discretizing the delay term and the periodic coefficient term,a portion of the actual time-domain state term is discretized in the FD method as well.Both SD and FD methods use a series of matrix multiplication to construct the FTM in another similar way,and they can be extended to predict the stability of a milling system with varying or multiple time delays.Insperger9compared SD with FD methods in a same scheme and proved that the 1st FD method converges slower than the same-order SD method.Later,second-order FD(2nd FD)11and high-order FD methods12–14were further developed to improve the convergence rate of FD methods.However,the construction of the FTM becomes more complicated,especially for multi-or varying-delay systems.Recently,Ding et al.15developed an efficient numerical integration(NI)method and Zhang et al.16proposed a compact Simpson method for the stability analysis of milling processes,respectively based on an integration scheme and a differential scheme.It was found that these methods are also analogous to temporal finite elements analysis and the Chebyshev collocation method in constructing the FTM.Besides,Zhou et al.17predicted the stability in end milling of aero-engine casings using an analytical method.Luo et al.18presented a new time-domain model of mechanics and dynamics of the cutter exit process.

This paper proposes an efficient,accurate,and compact stability prediction for a multi-delay milling system.The delay term and the periodic coefficient term are integrated as a comprehensive state term in the integral response of time-period DDEs which is approximated by a multi-step implicit Adams formula,and the time-domain state term is not discretized.A compact and arbitrary-order FTM is constructed by using a series of matrix multiplication.An improved precise time integration algorithm is used to calculatethe resulting exponential matrices rapidly.Furthermore,considering that different cutting force models and corresponding calibration accuracies of cutting force coefficients significantly affect the reliability of stability lobes19,20but the cutting force models in most of the above works are linear,an exponential force model is employed and a new approach is also presented to accurately calibrate exponential cutting force coefficients(ECFCs) and cutter run-out parameters (CRPs)simultaneously.

2.Modeling of the milling dynamics

The milling cutter is modeled as a mass-spring-damper system with two degrees of freedom(2-DOFs)respectively in the X direction(parallel to the tool feed)and the Y direction(perpendicular to the tool feed).It is assumed to be flexible as opposed to the rigid workpiece as shown in Fig.1.OG（t）is the geometric center of the milling cutter at the current cutting instant t.OG（t- τ）is the geometric center of the milling cutter at the previous cutting instant t- τ,where τ is the time delay.XRand YRare the orthogonal coordinate axes with their coordinate origins lying at OG（t）.j-1，j,and j+1 represent the previous,current,and next cutter teeth,respectively.kxand kyare the X and Y axial stiffness,respectively.cxand cyare the X and Y axial damping,respectively.FT（t）and FR（t）denote the tangential and radial cutting forces,respectively.Ω is the spindle rotation speed.hj（t）is the instantaneous uncut chip thickness of the jth tooth.θj（t）is the angular position of the jth tooth.Dynamic displacements of the system are excited by dynamic cutting forces,the mathematical representation of which is given by

Fig.1 Schematic of a 2-DOF milling process.

with

where mp,ζp,and ωnp（p=x，y）are the modal mass,damping ratio,and angular natural frequency,respectively.x（t）and y（t）are the dynamic displacements in the X and Y directions,respectively.Fx（t）and Fy（t）are the dynamic cutting forces in the X and Y directions,respectively.

2.1.Calculation of Fx（t）and Fy（t）

In order to accurately calculate Fx（t）and Fy（t）,the flat-end cutter considering the helix angle effect is divided into several disk-shape elements along the cutter axis with an equivalent axial length z0.Each element can be viewed as a simplified plane figure with its axial length being ignored.Thus,the tangential and radial cutting forces acting on the lth cutting element of the jth tooth can be formulated as

whereis a switch function that is used to determine whether the cutting element is removing material or not.hl，j（t）is the instantaneous uncut chip thickness related to the lth cutting element of the jth tooth at t.Sl，j（t）is the cutting area calculated by Sl，j（t）=hl，j（t）z0.Kl，j，T（t）and Kl，j，R（t）are respectively the tangential and radial cutting force coefficients related to the lth cutting element of the jth tooth at t,and both of them are expressed as the exponential functions of hl，j（t）in which kT，eT,kR，eRare the ECFCs.

Thus,at any cutting instant,the resultant forces in the X and Y directions can be calculated by summing up all the elemental forces,which can be expressed in the following form:

where the angular position related to the lth cutting element of the jth tooth at t can be given by

in which γl，jis the lag angle related to the lth cutting element of the jth tooth with respect to the bottom cutting element on the same tooth.Based on the known nominal geometrical radius R and cutter helical angle β , γl，jis calculated by

It should be noted in Eq. (4) that Ψl，k，k-1（k=1，2，...，j-1）is defined as the pitch angle between the kth and(k+1)th teeth of the lth cutting element.There are two cases for constant pitch milling cutters:(1)if there is no cutter run-out,Ψl，k，k-1is constant and equal to 2π/N in which N is the number of teeth;(2)if cutter run-out occurs,Ψl，k，k-1is varying for different k,which is the same as variable pitch cutters.As for variable helix cutters,Ψl，k，k-1is varying along different axial cutting elements of each tooth.

2.2.Calculation of hl，j（t）

If cutter run-out occurs,the rotation center is no longer the geometric center,as shown in Fig.2.ORis the rotation center of the milling cutter.XGand YGare the orthogonal coordinate axes with their coordinate origins lying at OG.Rl，jis the actual rotation radius related to the lth cutting element of the jth tooth.As a result,the run-out phenomenon will lead to changing radii and pitch angles of the teeth,which further alter hl，j（t）and regenerative time delay over the rotation period of the milling cutter.In order to take the cutter run-out effect into account,two CRPs are defined here:ρ denotes the run-out offset which is the distance between ORand OG;λ denotes the location angle which is defined in the bottom of the cutter and measured between the offset direction OROGand the tool tip direction of tooth j=1 relative to OG.The changing radius Rl，j（t）can be obtained by using the cosine law as follows:

For two successive cuts,the regenerative time delay between jth and(j-1)th teeth of the lth cutting element can be calculated by

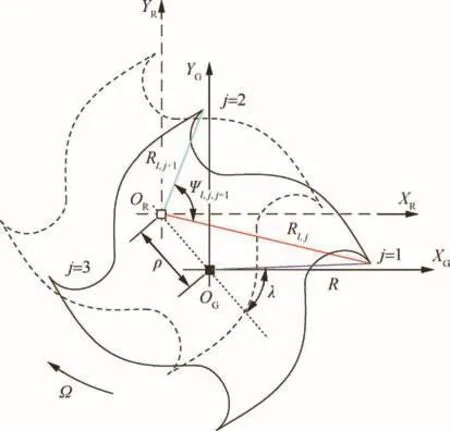
Fig.2 Cutter run-out model.

Then hl，j（t）can be determined by the following static and dynamic components:

where ftis the feed per tooth.n（t）and n（t- τl，j，j-1）are the dynamic displacements in the radial direction.Mathematically,one can have

2.3.Calibration of ECFCs and CRPs

In order to obtain accurate cutting force coefficients,a traditional linear force model usually requires a large number of slot milling experiments with a wide range of cutting parameters.This leads to a significant increase in time and economic costs.A few approaches21,22for calibrating nonlinear cutting force parameters have been proposed using only one or two cutting tests.As an alternative,a new calibration method with simple steps is proposed in this section only via a single cutting test.As mentioned previously,if the ECFCs and the CRPs are known in advance and the dynamic component of hl，j（t）is assumed to be 0,the total cutting forces at arbitrary instant iΔt can be calculated by Eq.(3),where i is an integer and Δt is the sample period in the measurement of cutting forces.Under the same cutting conditions,the total cutting forces in an actual milling process can also be measured by a dynamometer.With this understanding,one can yield

where（iΔt）,（p=x，y）denotes the measured cutting forces at iΔt.Fp（iΔt）（p=x，y）denotes the predicted cutting forces at iΔt which can be expressed by the following function form:

In fact,all the cutting instants over one revolution provide nsamgroups of Eq.(10)which depend on the spindle rotation speed and the sample frequency used in the measurement.Therefore,the problem of solving Eq.(10)can be transformed into the following nonlinear function minimization problem:

with

where ΔFq（iΔt），（q=x，y）denotes the deviation between predicted and measured forces at iΔt.S1is a weighted sum of the total squared force deviations respectively in the X and Y directions.α1and α2are two weighting factors,which estimate the contributions of the total squared force deviations of different directions to S1.Generally, α1and α2can be assigned values with a ratio of around 1:1.

Mathematically,P1is an unconstrained nonlinear optimization problem and does not provide any derivative information.Considering the advantage of solving unconstrained nonlinear optimization problems without derivatives,Powell’s algorithm is employed in our study,which adjusts calibration parameters until S1is at a minimum.The ECFCs and the CRPs can then be calibrated simultaneously.However,for constant pitch milling cutters,it should be noted that the sum of different magnitudes of cutting forces acting on each tooth with the same angular position is independent of the cutter’s radial run-out effect23,24;problem P1can thus be simplified into the following problem:

with

and

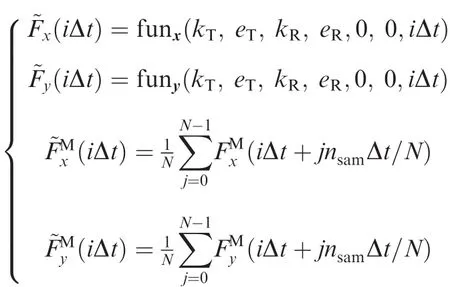
where the CRPs are set to be zero.Thus,the ECFCs can be calibrated firstly by solving problem P1,and the CRPs can then be calibrated by solving problem P2.Without loss of generality,the ECFCs and CRPs are calibrated using the second way in Section 5.

3.Proposed stability prediction method

In order to further improve the computational efficiency of original SD and FD methods,an Adams and precise time integration discretization(APD)method is proposed for predicting the stability of the multi-delay milling system governed by Eq.(1).Note that Eq.(1)is a nonlinear time-period DDE and its stability behavior can be analyzed by introducing a perturbation u（t）= ［ux（t），uy（t）］Tinto the desired periodic motion solution

where qs（t）is the stationary solution and is periodic at the spindle rotation period T=60/Ω, satisfying qs（t）=qs（t+T）,and the perturbation u（t）is considered as an infinitesimal which is associated with the stability behavior.Substituting Eq.(13)into Eq.(1),expanding into power series with respect to u（t）,and eliminating the higher-order terms can derive the following linear variational system:

where Hl，j（t）is the cutting force coefficient matrix which is periodic at T and can be expressed as

with

By introducing the state-space vector U（t）=［u（t），˙u（t）］T,Eq.(14)can be transformed into a state-space form with its order being halved as follows:

where A（t）is the system matrix and Bl，j（t）is the cutting force coefficient matrix,which can be given by

in which O and I are the 2×2 zero submatrix and identity submatrix,respectively.

In order to simplify the stability investigation on the system governed by Eq.(16),the system matrix can be replaced by its boundary value on a discrete time interval that will be introduced below,i.e.,Ad=A（dδ）where δ is the discrete time interval and d is the position index of each discrete time interval in T.As a result,Eq.(16)can be analytically reformulated into an integral equation with the initial value U（0）=U0as follows:

where ε is the variable of integration.Next,the spindle rotation period is discretized into m small time intervals,satisfying T=mδ.On each time interval dδ ＜ t＜ （d+1）δ，（d=0，1，...，m-1）,Eq.(17)can be given as

where the notation U（td）=Udis used for simplification purpose and the subsequent variables are done in the same manner.

In the Duhamel integral of Eq.(18),the involved state terms including exp（Ad（dδ + δ - ε））,Bl，j（ε）,and U（ε- τl，j，j-1）can be integrated into a comprehensive state term G（ε）by directly using their product as follows:

Hence,Eq.(18)can be rewritten as

Then,a multi-step implicit Adams formula based on forward difference is used to approximate the system response as follows:

where κ is the order of the implicit Adams formula.▽ris the difference operator and Eris the coefficient related to▽rGd,which satisfy25

where s is the variable of integration.Substituting Erand▽rGdinto Eq.(21)leads to

where

with

and Λ1，Λ2，...，Λκare the coefficients of Gd，Gd+1，...，Gd+κ,which can be easily calculated via Eqs.(22)and(23)and are given in Table 1 for κ ≤ 4.mj，j-1is the approximation parameter of the time delay corresponding to the actual pitch angle between the jth and(j-1)th teeth due to the occurrence of cutter run-out,which satisfies mj，j-1=round（τl，j，j-1/δ）andConsidering the advantages of efficiently calculating exponential matrices without solving any inversematrices,the resulting exponential matrices in Eq.(26)are calculated by using the PTI algorithm.26Table 2 provides the pseudo-codes of calculating Φ1and Φ-κ+1via the PTI algorithm.In the table,pexis the precision exponent of the PTI algorithm,and η is the precisely divided time interval,satisfying η = δ/2pex.Since the time interval δ is already very small,η will be an extremely small time interval,and pex=2 is large enough in the computation.

Table 1 Coefficients for the implicit Adams formula.

It is noted that half of the elements in the system matrix are zero and identity submatrices.Hence,the power of the system matrix Aqd，（q=1，2，3 and 4）involved by the PTI algorithm in Table 2 can be calculated rapidly using the following recursive formulas:

where

with

and Oq,Iq,Wq,and Qq, （q=1，2，3 and 4）are intermediate matrix variables.Combining the original PTI algorithm with the rapid computation of the qth power of the system matrix gives an improved PTI algorithm,which can significantly improve the computational efficiency.

Table 2 Pseudo-codes for calculating Φ1and Φ-κ+1.

After that,a concise 2(m+2)-dimensional discrete dynamical map can be defined as

where

in which the ‘× ’subscripts are used to distinguish the dimension of each element in matrix Fd.O4×4and O2m×2are zero matrices.I2m×（2m+2）and P4×2mare respectively

and the upper and lower brackets denote the total column dimension of the respective included elements.

Now,a unified arbitrary-order FTM F of the milling dynamic system over the discrete time period can be established as

Finally,the stability lobes of the multi-delay milling system can be predicted based on the Floquet theory.They are drawn in the cutting parameter space when the eigenvalues of the FTM are in modulus equal to 1.The milling process will be stable if a cutting parameter combination is chosen in the lower region of stability lobes;otherwise,it will be unstable.

4.Simulation comparison

To compare the convergence rate and computational efficiency of the proposed APD method with those of typical and recently proposed methods,a common benchmark example is employed with a single delay and without considering the helix angle and cutter run-out effects.9For comparison purpose,the FTM of the proposed method is simplified into the following form of a single-DOF system with a single delay that is equal to the tooth passing period:

where mtis now the approximation parameter regarding the tooth passing period and

with

Table 3 Parameters of the single-DOF milling model.9

and the involved elements in P2×mtcan be deduced following the same procedures from Eq.(16)to Eq.(25)which are not repeated here.The system parameters and the tool parameters are listed in Table 3,9where the single-DOF system is recognized in the X direction.

4.1.Convergence analysis

Convergence analysis has been normally used in some existing literature9,11–16for algorithm error estimation.It utilizes a local discretization error which is defined as the deviation between an exact solution and an approximate solution to estimate the rate of convergence.It has been proven that the deviation between the exact critical eigenvalue μ0and the approximate critical eigenvalue μ tends to be 0 when a large approximation parameter m is adopted.8Here,μ0is determined by the 1st SD method with m=600 as a reference.Four cutting test points are selected for the convergence analysis as shown in Fig.3.The cutting test points shown in Fig.3(a)–(c)have the same spindle speed of Ω=5000 r/min and different axial cutting depths of ap=0.2,0.5,and 1 mm,which are often chosen as the benchmark points to compare convergence rates between different methods.Similarly,the cutting test point in Fig.3(d)shows a comparison between the 4th-order FD method and the proposed APD method in 1st-4th order forms.As shown in Fig.3(a)–(c),the convergence curve of the proposed APD method in the first-order form(1st APD)is closer to the horizontal axis than those of other methods,especially in small approximation parameter cases.From Fig.3(d),even compared to the high-order FD method,namely the 4th FD method,the proposed APD method in first-order forms can still achieve a faster rate of convergence.It can also be seen that the proposed APD method can converge faster by changing into a higher-order form.However,when a form beyond the second order is adopted,the convergence curve is not smooth anymore,even showing a phenomenon that the improvement of the rate of convergence by the fourth-order form is no more than that by the threeorder form,which is called Runge phenomenon and attributed to the numerical instability caused by increasing equidistant points in Lagrange interpolation.27Thus,a higher-order form beyond the third order for the proposed APD method is unnecessary.

Fig.3 Convergence analysis with different cutting test points.

4.2.Comparison with SD methods

As mentioned previously,the SD and FD methods are representative methods in the discrete time domain.In order to verify the effectiveness of the proposed method,a widely used benchmark example for low-speed milling is employed.The SLDs are determined by the SD,FD,and proposed APD methods.Computation efficiency and prediction accuracy are simultaneously investigated.Process parameters of the milling dynamical system are derived from the above subsection.The SLDs for low-speed milling are illustrated in Fig.4,which are determined by the 0th SD,1st SD,and proposed 1st APD methods with a different approximation parameter m.The stability boundaries determined by the 1st SD method with m=300 is presented by red color for reference.The SLDs are calculated over a 400×200 sized grid of cutting parameters within the spindle speed Ω ∈ ［2 × 103，3 × 103］r/min and the axial cutting depth ap∈ ［0，2×10-3］m.The computational times of the three methods are also summarized in Fig.4.It can be seen that the proposed APD method has a much better prediction accuracy than that of the SD method and costs less computational time.

4.3.Comparison with FD methods

Since the 1st FD method was firstly proposed in 2010,some improved high-order methods have been developed one after another to achieve more accurate prediction.In Ref.14,Ozoegwu et al.proposed hyper third-order FD methods based on the least squares approximation theory and proved that the fourth-order(4th FD)method gives the best stability prediction at the top of lobbing effect.In a benchmark example of high-speed milling,a comparison between the FD methods and the proposed APD method is conducted.The newly published 4th FD method and the well-accepted 1st FD and 2nd FD methods are selected from FD methods.Accordingly,the corresponding fourth-order, first-order,and second-order forms are adopted for the proposed APD method.

Fig.4 Comparisons of the SLD and computational time between the SD method(0th SD and 1st SD methods)and the proposed 1st APD method in low-speed milling.

Fig.5 Comparisons of the SLD between the FD methods(1st FD,2nd FD,and 4th FD methods)and the proposed APD method(in 1st,2nd,and 4th-order forms,respectively)in high-speed milling.

Fig.6 Comparisons of computational time between FD method and proposed APD method.

The SLDs illustrated in Fig.5 are calculated over a 400×200 sized grid of cutting parameters within the spindle speed Ω ∈ ［6 × 103，10 × 103］r/min and the axial cutting depth ap∈ ［0，4×10-3］m.The SLD determined by the 2nd FD method with m=300 is presented by red color for reference.It can be seen that the proposed method is more accurate than the corresponding FD method.In terms of the so-called lobbing effect,it can be seen in the enlarged region of Fig.5,the proposed method in the fourth-order form gives a more accurate prediction than that of the 4th FD method.

Fig.7 Experimental setup.

Table 4 Cutting parameters for calibrating ECFCs and CRPs.

Table 5 Calibrated ECFCs and CRPs.

In terms of computation efficiency,as shown in Fig.6,the proposed method is highly efficient.When the first-order form is adopted,the proposed method costs less computational time than that of the efficient 1st FD method.When the fourthorder form is adopted,it costs less computational time than that of the 2nd FD method.Most importantly,with an increasing order,there is only a slight increase in computational time for the proposed APD method.In Fig.6,two arrows in red color denote the increasing trend in computational time of FD methods from first-order to fourth-order and the proposed APD method respectively in first-order to fourth-order forms.It can be found that both increasing trends are nearly linear,at least over the relatively small approximation orders κ ≤ 4,and the increasing trend of the proposed method is significantly lower than that of FD methods.

5.Experimental verification

5.1.Experimental calibration of ECFCs and CRPs

Fig.9 Frequency response function for the machine-tool structure in the X and Y directions.

Table 6 Modal parameters for the machine-tool structure.

Two down milling tests on a five-axis CNC milling machine DMU50 are firstly carried out without lubrication to validate the proposed calibration method.The experimental setup is shown in Fig.7.The cutting conditions are listed in Table 4.Aluminum alloy 6061 is adopted as the workpiece material,which is widely used as an aerospace part material.A two fluted end mill cutter with a diameter of 12 mm and a helix angle of 35°is employed,and the cutter overhang length is 70 mm.A Kistler Dynamometer 9257 B with a sampling frequency of 15 kHz is used to measure the cutting forces in the X and Y directions.

Fig.8 Comparisons between measured and predicted cutting forces.

Table 7 Cutting parameters for verifying the accuracy of the predicted SLD.

Fig.10 Predicted SLD and chatter results from experiments.

The ECFCs and CRPs are calibrated using the proposed calibration method,in which a fractional tolerance of 10-4is used during the process of optimization.The calibrated results based on Test 1 converge within 3726 iteration steps using 2.9 min in a desktop computer with Intel(R)Core(TM)-i5-4430 CPU@3.0 GHz and 8 GB memory,and the calibrated results are listed in Table 5.The result of Fig.8 shows that the predicted cutting forces using the calibrated results agree well with the experimental cutting forces,which indicates that the proposed calibration method is effective.

5.2.Experimental verification for the proposed APD method

The modal at the tool tip is determined by a hammer test.Fig.9 provides the real and imaginary parts of the frequency response function for the machine-tool structure along the X and Y directions.With the system identification approach used in Ref.28,modal parameters are derived and listed in Table 6.In the following simulation results,only Mode 2 in Table 6 is considered for the proposed APD method to predict the SLD.This is because Mode 2 is significantly more flexible than other modes.A series of cutting tests is carried out to verify the proposed method,and all of them are conducted without lubrication in a down-milling mode.Other cutting conditions are listed in Table 7.

5.3.Results and discussion

The decision-making about whether chatter has occurred or not for each cutting test is done by chatter marks left on the machined surface and by the analysis of measured force signals.The chatter results and the SLD predicted by the proposed method are illustrated in Fig.10,where the triangles marked in red color stand for the chatter cases in the experiment,and the pentagrams in green color denote stable cutting.Fig.10 also provides the surface quality after milling,measured cutting forces during one full cut,and the corresponding Fourier spectra of cutting tests 5 and 8,where f denotes the tooth passing frequency of each cutting test.It can be seen that cutting test 5 is stable and its Fourier spectrum is dominated by its tooth passing frequency and the harmonic frequencies of the tooth passing frequency.Cutting test 8 is at a spindle speed of 5000 r/min which is 200 higher than that of cutting test 5,and chatter vibrations occur in this cutting test.From the Fourier spectrum of cutting test 8,it can be seen that the maximum chatter frequency is 19.59 times its tooth passing frequency,which is close to the second-mode frequency of the machine-tool structure.When the spindle speed is increased by an extra 200 r/min on the basis of cutting test 8,namely to cutting test 10,the chatter vibrations disappear again.The above experimental results indicate that the predicted SLD is accurate.In other words,the proposed method in this paper is valid and has the potential to be used by industrial users for selecting proper cutting parameter combinations to accomplish chatter-free milling operations.

6.Conclusions

In a milling process,accurate and efficient prediction of chatter stability depends on accurate modeling of milling dynamics and the stability prediction method.From this study,the following conclusions can be drawn:

(1)A multi-delay stability system is built on an exponential force model,and both helix angle and run-out effects are taken into account.

(2)A new calibration approach is presented to determine the ECFCs and CRPs simultaneously.

(3)For the modeled multi-delay milling system,an efficient multi-order APD method is further proposed to predict its stability.

(4)Compared to typical methods in the discrete time domain,the proposed method is highly efficient and accurate with a fast rate of convergence and a compact multi-order form.

(5)A series of cutting tests has demonstrated the practicability and effectiveness of the proposed method.

(6)The proposed method also has the potential ability to solve the stability problem of milling processes with varying or multiple time delays which may be introduced by variable helix or pitch tools,varying spindle speed,etc.

Acknowledgments

This study was co-supported by the National Natural Science Foundation of China (Nos.51525501,11290143,and 51621064)and the Science Challenging Program of China(No.JCKY2016212A506-0102).

1.Quintana G,Ciurana J.Chatter in machining processes:a review.Int J Mach Tool Manu 2011;51(5):363–76.

2.Altintas Y.Manufacturing automation:metal cutting mechanics,machine tool vibration,and CNC design.2nd ed.Cambridge:Cambridge University Press;2012.

3.Altintas Y,Budak E.Analytical prediction of stability lobes in milling.CIRP Ann –Manuf Technol 1995;44(1):357–62.

4.Budak E,Altintas Y.Analytical prediction of chatter stability in milling—Part I:General formulation.J Dyn Syst Meas Control 1998;120(1):31.

5.Bayly PV,Halley JE,Mann BP,Davies M.Stability of interrupted cutting by temporal finite element analysis.J Manuf Sci Eng 2003;125(2):220.

6.Butcher EA,Bobrenkov OA,Bueler E,Nindujarla P.Analysis of milling stability by the chebyshev collocation method:algorithm and optimal stable immersion levels.J Comput Nonlinear Dyn 2009;4(3):31003.

7.Insperger T,Stépán G.Semi-discretization method for delayed systems.Int J Numer Methods Eng 2002;55(5):503–18.

8.Insperger T,Stépán G.Updated semi-discretization method for periodic delay-differential equations with discrete delay.Int J Numer Methods Eng 2004;61(1):117–41.

9.Insperger T.Full-discretization and semi-discretization for milling stability prediction:some comments.Int J Mach Tools Manuf 2010;50(7):658–62.

10.Ding Y,Zhu LM,Zhang XJ,Ding H.A full-discretization method for prediction of milling stability.Int J Mach Tools Manuf 2010;50(5):502–9.

11.Ding Y,Zhu LM,Zhang XJ,Ding H.Second-order fulldiscretization method for milling stability prediction.Int J Mach Tools Manuf 2010;50(10):926–32.

12.Liu YL,Zhang DH,Wu BH.An efficient full-discretization method for prediction of milling stability.Int J Mach Tools Manuf 2012;63(5):44–8.

13.Quo Q,Sun YW,Jiang Y.On the accurate calculation of milling stability limits using third-order full-discretization method.Int J Mach Tools Manuf 2012;62:61–6.

14.Ozoegwu CG,Omenyi SN,Ofochebe SM.Hyper-third order fulldiscretization methods in milling stability prediction.Int J Mach Tools Manuf 2015;92:1–9.

15.Ding Y,Zhu LM,Zhang XJ,Ding H.Numerical integration method for prediction of milling stability.J Manuf Sci Eng 2011;133(3):31005.

16.Zhang Z,Li HG,Meng G,Liu C.A novel approach for the prediction of the milling stability based on the Simpson method.Int J Mach Tool Manu 2015;99:43–7.

17.Zhou X,Zhang DH,Luo M,Wu BH.Chatter stability prediction in four-axis milling of aero-engine casings with bull-nose end mill.Chin J Aeronaut 2015;28(6):1766–73.

18.Luo M,Mei JW,Zhang DF.Time-domain modeling of a cutter exiting a workpiece in the slot milling process.Chin J Aeronaut 2016;29(6):1852–8.

19.Elías-zún˜iga A,Martínez-lópez A,Rodríguez C.Stability predictions for end milling operations with a nonlinear cutting force model.J Manuf Sci Eng 2009;131:1–6.

20.Wan M,Wang YT,Zhang WH,Yang Y,Dang JW.Prediction of chatter stability for multiple-delay milling system under different cutting force models.Int J Mach Tools Manuf 2011;51(4):281–95.

21.Azeem A,Feng HY,Wang L.Simplified and efficient calibration of a mechanistic cutting force model for ball-end milling.Int J Mach Tools Manuf 2004;44(2):291–8.

22.Wan M,Zhang WH,Dang JW,Yang Y.New procedures for calibration of instantaneous cutting force coefficients and cutter runout parameters in peripheral milling.Int J Mach Tools Manuf 2009;49(14):1144–51.

23.Wu BH,Yan X,Luo M,Gao G.Cutting force prediction for circular end milling process.Chin J Aeronaut 2013;26(4):1057–63.

24.Wan M,Zhang WH,Tan G,Qin GH.New cutting force modeling approach for flat end mill.Chin J Aeronaut 2007;20(3):282–8.

25.Hairer E,Nørsett SP,Wanner G.Solving ordinary differential equations I.2nd ed.Berlin Heidelberg:Springer;1993,pp.357–61.

26.Zhong WX,Williams FW.A precise time step integration method.Proc Inst Mech Eng Part C –J Mech Eng Sci 1994;208(6):427–30.

27.Berrut J-P,Trefethen LN.Barycentric Lagrange interpolation.SIAM Rev 2004;46(3):501–17.

28.Schmitz TL,Davies MA,Medicus K,Snyder J.Improving highspeed machining material removal rates by rapid dynamic analysis.CIRP Ann – Manuf Technol 2001;50(1):263–8.