An adaptive fast fixed-time guidance law with an impact angle constraint for intercepting maneuvering targets

Yao ZHANG,Shengjing TANG,Jie GUO

Key Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China

1.Introduction

In the last few decades,intelligent and maneuvering targets have been regarded as serious threats in modern warfare,and to intercept them,there is a great need to develop advanced guidance laws by using modern control techniques.A guidance law,as an indispensable part in the course of maneuvering target interception,determines the flight trajectory of an interceptor and has direct influence on the terminalmiss distance.1As is well known,the Proportional Navigation Guidance(PNG)law has been widely applied in weapon guidance during the last few years due to its convenient implementation and efficiency for stationary as well as moving targets with weak maneuver.2However,with the increasing requirement of defense tasks,especially for intercepting a highly maneuverable target,the performance of PNG is difficult to meet high demands of damage ability with the increase in target available maneuverability.Therefore,obtaining a small enough miss distance is no longer the only objective in some practical intercepting missions.In some missions,interceptors are required not only to achieve accurate attack with the minimum miss distance,but also to have a desired impact angle at the time of interception,which provides the best damage effect by increasing the effectiveness of warheads against maneuvering targets.3As for the progress of homing guidance and precious attack in recent years,robust terminal angle constraint guidance law design has attracted great attention and become one of the most important evaluation indicators for missile design,4since it can improve the overall guidance performance,for instance,increasing kill probability,improving penetration capability,and reducing the warhead size.5Such a requirement is quite significant for interceptors when attacking large ships,tanks,ballistic missiles,as well as fast and maneuvering aircrafts.6

The issue of intercepting a target from a desired terminal impact angle,including a stationary target,7non-stationary non-maneuvering target,8and maneuvering target,9,10has been studied extensively for a few decades.Various guidance laws,such as optimal guidance,11trajectory shaping guidance,12time varying based PNG,13and an intelligent optimization method,14have been derived to guarantee imposing a predetermined impact angle.However,these guidance laws need to estimate the function of time-to-go tgo,which is a formidable challenge.In order to satisfy vital requirements including zero miss distance and a terminal impact angle constraint without an estimation of tgo,in recent years,terminal angle constraint guidance laws based on Sliding Mode Control(SMC)have become a research hotspot.In Ref.15,an impact angle constraint guidance law was proposed for unpowered lifting reentry vehicles against stationary targets.Besides,an SMC-based guidance law that enables imposing a desired intercept-angle was designed in Ref.16,and its applications in head-on,tail-chase,and head-pursuit interception engagements were analyzed.17Note that the conventional SMC guidance law is well known for its simplicity and robustness,but the states when the sliding mode is established can only satisfy asymptotical stability,which implies that these existing guidance laws can only ensure an interception with a prespecified impact angle through asymptotic convergence rather than finite-time convergence.As is well known,in some guidance applications,like air-to-air combat situations,the assurance of interception with a desired impact angle within a finite time is very necessary.Besides faster convergence rates,finite-time control laws usually achieve higher accuracies,better disturbance rejection features,and stronger robustness against uncertainties.18

Among the SMC community,Terminal Sliding Mode Control(TSMC),established by a nonlinear switching manifold(i.e.,sliding surface),obtains a finite-time convergence property stabilizing system states within a prescribed time without imposing strong control energy.19Recently,the TSMC method has been used in missiles20and unmanned aerial vehicles21guidance applications.Especially,an impact angle control guidance law,based on finite-time convergence stability and sliding mode control for moving targets with a slow speed,was proposed in Ref.2.Besides,in Ref.6,guidance laws with impact angle constraints,which ensure finite-time convergence to a desired impact angle,based on TSMC for stationary,constant velocity,and maneuvering targets,were developed.Although the guidance laws proposed in Refs.6,22provide finite-time convergence,that is,an interceptor is able to align itself with an impact angle frame within a finite time,both have the drawback of a potential singularity problem when the error being steered to a very small value.The same singularity problem can also be found in a Finite-Time Guidance law(FTGL)that only focuses on interception without considering impact angle constraints.23Therefore,for the purpose of avoiding the singularity while preserving the finite-time convergence feature,an impact angle constrained guidance law,based on Nonsingular Terminal Sliding Mode Control(NTSMC)for stationary and non-maneuvering moving targets with a constant speed,was firstly proposed in Ref.24.Similarly,a finitetime convergent terminal angle constrained guidance law was also proposed in Ref.25for guided bombs against stationary targets.However,these guidance laws developed in Refs.24,25are limited to stationary or moving targets without maneuvering cases.Especially,Kumar et al.proposed a Nonsingular Terminal Sliding Mode Guidance Law(NTSMGL)with impact angle constraints,and analyzed impact angle constraints situations for stationary targets,constant-speed targets, and maneuvering targets under different initial engagement geometries and desired impact Line-Of-Sight(LOS)angles.The designed NTSMGL in Ref.26gave a great performance in each situation and was convincing for different attack missions.This work,however,has three main limitations:(A)the chattering problem;(B)a long path length and a long strike time;(C)requiring information on the upper bound of target maneuver.In reality,target acceleration cannot be obtained in advance due to the complexity of unpredictable target maneuver pro files.Thus,a quite large robust switching gain is required,which in turn will lead to overestimation of the switch control input,increase control energy waste,and worsen the undesired chattering phenomenon.Up to date,a continuous composite Fast NTSMGL(FNTSMGL)was proposed in Refs.27by using a fast NTSMC approach and a general disturbance observer,where the proposed guidance law required no information on target maneuver and mitigated the chattering problem effectively.Furthermore,a guidance law designed in Ref.28employed the fast TSMC method and an extended state observer,which could optimize trajectories obviously with a short path length and a short strike time.Nevertheless,it should be pointed out that all these guidance laws based on the finite time convergence stability theory cannot guarantee system convergence within bounded finite time,that is to say,an exact convergence time cannot be obtained in the initial design of an guidance system.We are required to select appropriate initial conditions of an interceptor to achieve a desired fast convergence property with a desired settling time.

Therefore,in contrast to existing finite-time control,the‘ fixed-time’stability proposed by Polyakov29can ensure system convergence within bounded time regardless of initial conditions,which prohibits its application into a practical spacecraft system if the settling time could be prescribed without having the knowledge of initial conditions.Inspired by this attractive feature, fixed-time stability has found applications in attitude tracking control30and fault tolerant control31for spacecraft.However,there are few achievements in applying fixed-time stable control to missile guidance law design.Zuo32proposed a fixed-time stable first-order system with application to the network consensus problem,and then provided a nonsingular fixed-time terminal sliding mode control method in Ref.33for a class of second-order dynamic systems with matched uncertainties.However,the convergence time of the Nonsingular Terminal Sliding Mode(NTSM)controller is not an optimal one,and a characteristic of globally fast convergence is not obtained;additionally,the method employing an approach of eliminating the singularity problem is complicated.

Motivated by the above discussion,this paper proposes a fast fixed-time convergent NTSM control approach and investigates the feasibility of the impact angle constrained guidance law for intercepting maneuvering targets by introducing adaptive gain nonlinear methods implemented using the proposed fast fixed-time SMC technique to estimate the bound of target maneuver.The main contributions of this study relative to most of the existing guidance laws are the following two aspects.Firstly,a novel Fast Fixed-Time NTSM(FFTNTSM)is proposed and applied to the impact angle constrained guidance design.Consequently,it can guarantee finite-time system stabilization independent on initial conditions without singularity and achieve global fast convergence both far away from and at a close range of the control objective.Secondly,an Adaptive Fast Fixed-Time NTSM Guidance Law(AFFTNTSMGL)is designed for maneuver target interception with a desired impact angle,which ensures a finite-time reachability of the LOS angle tracking error and LOS angular rate into a small neighborhood of the origin regardless of the initial launched conditions.A continuous and nonsingular property is achieved by introducing a continuous piecewise function to the sliding mode manifold.In comparison with the existing fruitful results on existing guidance laws,23,26,27,33the proposed guidance law applies a simpler structure to overcome the singularity problem and overestimation of the switch gain without any knowledge of target maneuver.Besides,it provides globally faster convergence rates both far away from and in a small neighborhood of the origin.

This paper is organized as follows.Section 2 presents some preliminary concepts.In Section 3,the FFTNTSM is established and the AFFTNTSMGL is developed to intercept maneuvering targets with impact angle constraints.Next,results of numerical simulations to demonstrate the performance and superiority of the proposed guidance law are given in Section 4,followed by conclusions in Section 5.

2.Preliminary concepts

2.1.Problem formulation

Consider an impact angle constrained interception problem within the perpendicular plane and 2D planar homing engagement geometry between a missile and a target as depicted in Fig.1(a).The missile and the target are supposed to have velocities Vmand Vt,their flight path angles are denoted by γmand γt,and their normal accelerations are amand at,respectively.Besides,the relative range between the missile and the target is r,and the LOS angle is given by θ.For simplicity,assuming that the missile and the target are regarded as point masses moving in the perpendicular plane with constant velocities,the corresponding kinematic engagement equations are given by

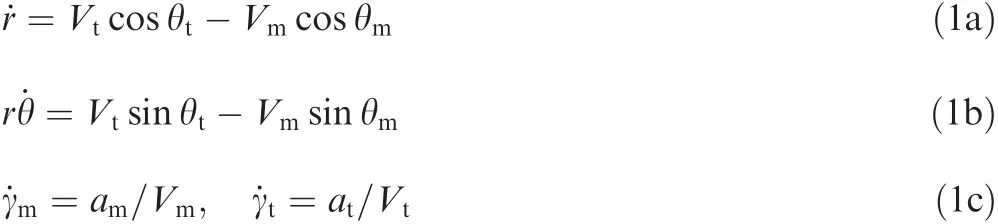
where θm= γm- θ and θt= γt- θ.

Differentiating Eqs.(1a)and(1b)with respect to time,we have

Fig.1 Planar engagement between a missile and a target.

Generally,the tangential acceleration along the missile’s velocity cannot be controlled in the terminal phase,5and therefore it is verified from many existing research that only the second-order dynamics between the missile’s normal acceleration amand the LOS angle θ as shown in Eq.(2b)is applied to the design guidance law in the terminal phase.Besides,note that the control input,i.e.,the missile normal acceleration am,is multiplied by the term cosθm,and it is obviously found that the cases θm= ±π/2,which cause cosθm=0,lead to control singularity.Under such conditions,the missile cannot regulate the LOS angular ratesuccessfully.In Ref.6,it has been demonstrated that if θm=±π/2,then˙γm-˙θ≠0.Therefore,the scenarios θm= ±π/2 are not stable equilibrium points,and the guidance system trajectory just across the points θm= ±π/2 will not stay on them.As a result,the normal acceleration amcan be used to control the LOS angle θ.In addition,considering the physical saturation of the actuator,the missile’s available overload is always bounded and the normal acceleration amsatisfies|am|≤.In order to remove the dependence of the guidance law on the term cosθm,a new variable is introduced as φ =am+atcosθt-amcosθmfrom Ref.27,and then the LOS angular rate dynamics in Eq.(2b)can be rewritten as

Remark 123.Technically,the missile intercepting the target by impact(i.e.,hit-to-kill)occurs when r≠0 but belongs to the interval r0∈[rmin,rmax]=[0.1 m,0.25 m].

Assumption 123.The target acceleration atis bounded and satisfies|at|≤for all t≥ 0,whereis a positive unknown constant.In this paper,we consider many kinds of target maneuvers,for example,constant maneuver,periodic maneuver,ramp maneuver,and high-order maneuver.The maximum accelerationof the target is bounded but not required to know.

As is well known,achieving a desired impact angle is an extra objective along with the conventional requirement of interception.The impact angle,denoted by θimpin Fig.1(b),is defined as the intersect angle between the velocity vectors of the missile and the target during interception and is formulated as

where γtfand γmfrepresent the flight path angles of the target and the missile,respectively,in the process of interception.The guidance laws for interception at a desired impact angle within a finite time are designed under the assumption that the target-to-missile speed ratio υ satisfies υ=Vt/Vm＜1.Hereon,from Ref.26,it is easy to establish a relationship between the impact and LOS angles,that is,a unique LOS angle exists for a particular impact angle in most engagement scenarios.As shown in Fig.1(c),at the time of interception,the missile and the target are on a collision course,and thus,there exists

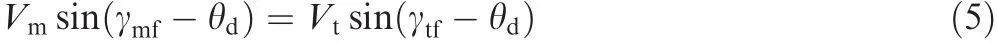
where θdrepresents the desired LOS angle at the time of interception.Additionally,from Eq.(1b),we get r˙θ=0.Then,the relation

is derived and Eq.(6)achieves the purpose that the impact and LOS angles have the one-to-one correspondence as discussed in Ref.26,which is bene ficial to further research.Especially,when θimp=kπ,k= ±1，±2，...,head-on and tail-chase scenarios can be represented.

2.2.Control objective

In this paper,the control objective is designing the interceptor lateral acceleration amto guarantee that the condition θ = θdis achieved at the time of interception.Considering that the guidance law is designed for a general case of a maneuvering target,a desired terminal LOS angle θdcan be pre-specified with a constant value,and some necessary data such as θ,˙θ,r,˙r,and γmcan be provided availably.Let x1= θ - θdand x2=˙θ,and then substituting them into Eq.(3)yields

where f=-,g=-1/r,and d=φ/r.

Assumption 2.In Eq.(7),d defines an unknown lumped disturbance of the target.Based on Remark 1 and Assumption 1,the following inequality holds:

Therefore,d is a bounded unknown lumped external disturbance,i.e.,|d|≤ Δ，where Δ is an unknown positive constant.

The ultimate purpose of this concept is to develop a guidance law amso that it can ensure not only that the missile has a small miss distance,but also that the LOS angle error x1and the LOS angular rate can be steered to a small enough neighborhood near zero in finite time in the presence of unknown external disturbance and,consequently,a quasiparallel approach can be realized.

3.Design of adaptive FTNTSM guidance law

3.1.Fast fixed-time nonsingular terminal sliding mode

As is known,the finite-time stability cannot guarantee system convergence within bounded settling time independent on the initial condition,which prohibits its application into practical interception missions if the initial condition is unavailable to be selected easily or even unknown.An inappropriate selection on the initial condition causes an undesired time or in finite time to accomplish command tracking.Obviously,such an in finite convergence time is not an option during highly critical terminal intercepting phases.Moving further on,in 2012,Polyakov29proposed a fixed-time stability concept as follows.

Lemma 129.Consider the system of differential equations as

where x∈ Rn,F（x）:D → Rnis continuous in an open neighborhood D⊆Rnof the origin and F（0）=0.The origin is said to be a fixed-time stable equilibrium point if it is globally finitetime stable with a bounded settling time function T（x0）,that is,there exists Tmax＞ 0 so that T（x0）＜ Tmax，∀x0∈ Rn.

In 2015,Zuo32,33proposed a fixed-time terminal sliding surface s=x2++,where m1,n1,p1,and q1are positive odd integers satisfying m1＞n1,p1＜q1＜2p1,α1＞ 0,and β1＞ 0.When s=0,there exists a fixed-time stable systemwith a bounded settling time T ≤ n1/［α1（m1-n1）］+q1/［β1（q1-p1）］.However,consider the system=0 with α1=1,and the eigenvalue satisfies ∂x2/∂x1=-/n1.Due to m1＞ n1,the eigenvalue tends to be zero at the origin,which implies that the convergence rate is in finitely small.That is to say,as shown in Fig.2,when the initial state satisfies|x0|＜1,the convergence rate is slower than that of the case m1/n1=1;when the initial state is far from the origin,the convergence rate is faster than that of the case m1/n1=1.

To this end,it is imperative to enhance the convergence rate of the existing fixed-time convergent SMC approach and achieve fast fixed-time convergence both far away from and in a small permissible range of the origin.Therefore,a novel fast fixed-time stable system is established.

Lemma 2.Consider the following differential equation:

where

κ =0.5+0.5 × m1/n1+ （0.5 × m1/n1-0.5）sign（|ξ|-1）,α0＞ 0,β0＞ 0,and m1,n1,p1,and q1are positive odd integers that satisfy m1＞n1and p1＜q1.Then,Eq.(10)is fixed-time stable,and the settling time T is bounded by

Proof.The differential equation in Eq.(10)can be rewritten as

Introduce a new variable as χ =z（q1-p1）/q1and the expression for the first equation in Eq.(12)is rewritten as

Let ξ = ［（m1-n1）q1］/［n1（q1-p1）］,and we have

Fig.2 Phase plot of the system x2+=0 with different values of m/n.

Similarly,the expression for the second equation of Eq.(12)is rewritten as

Therefore,by solving Eqs.(14)and(15)for convergence time,the upper bound of convergence time can be estimated as

The proof is completed.□

Remark 2.Note that the fixed-time stable system presented in this paper achieves faster global convergence than that of the system proposed by Zuo.The proposed system introduces a linear term z instead of a nonlinear term zm1/n1in Zuo’s approach in the vicinity of the origin,thereby providing a fast convergence rate both far away from and in a small permissible range of the origin.

Consider the following stable systems:(A)the proposed fast fixed-time stable system˙z=-zκ-zp1/p1with m1/n1=5/3 and p1/q1= 3/5,(B)the fixed-time stable system ˙z=-zm1/n1-zp1/q1proposed by Zuo32,33,and (C)the conventional finite-time stable system˙z=-z-zp1/q1.Different from the finite-time stable system,the proposed fixed time stable system can guarantee stabilization within bounded time independent on initial conditions.Meanwhile,the system achieves fast convergence.Next,a comparative simulation among the above stable systems is given to show the superiority of the proposed fixed-time stable system.Fig.3 shows the convergence time of the above stable systems under different initial conditions.As Fig.3 clearly verifies,the convergence time of the fixed-time stable systems is upper bounded by a constant,while the convergence time of the finite-time stable system becomes longer if the initial state is farther from the origin.Besides,it takes less time for the proposed fast fixed-time stable system to converge to zero than that of Zuo’sapproach.Simulation results demonstrate the superiority of the proposed fixed-time stable system.

Fig.3 Convergence time versus the initial condition for different stable systems.

Fig.4 Weaving target interception with different initial heading angles under the AFFTNTSMGL proposed by fixed-time stability.

A novel fast fixed-time TSMC strategy for an arbitrary uncertain second-order system is presented,and the corresponding sliding mode manifold can be constructed as

where

κ1=0.5+0.5 × m1/n1+ （0.5 × m1/n1-0.5）sign（|z|-1）,α1＞ 0,β1＞ 0,and m1,n1,p1,and q1are positive odd integers satisfying m1＞n1and p1＜q1＜2p1.Then,the fast fixed-time terminal sliding mode dynamics is obtained as

3.2.Guidance law design

According to the above analysis,in this section,we need to design the guidance law amfor the guidance system in Eq.(7)using the design principles of the SMC theory.Firstly,the fast fixed-time NTSM manifold s is given by

Then,from Eqs.(7)and(18),the time derivative of the proposed sliding manifold s in Eq.(19)can be obtained as

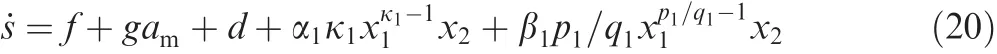
In order to make the system trajectories fast converge to the designed sliding manifold s in Eq.(20)from arbitrary initial conditions,a fast fixed-time terminal sliding mode reaching law can be selected as

where κ2=0.5+0.5 × m2/n2+ （0.5 × m2/n2-0.5）sign（|s|-1）, α2＞ 0,β2＞ 0,and m2,n2,p2,and q2are positive odd integers satisfying m2＞n2and p2＜q2.Substituting Eq.(20)into Eq.(21),we have

where the saturation function is defined as

Remark 3.In Eq.(22),a saturation function is introduced to limit the amplitude of the singularity termin the control input.In order to guarantee the sliding manifold reach to zero outside the singularity area,xmaxcan be chosen to satisfy

where|x1|＜x1,max.

Unfortunately,in a practical intercepting guidance process,the lumped disturbance d containing target maneuver acceleration may not be easily obtained.Usually,we choose a switching function ηsign（s）to compensate the unknown disturbance,where η is the robust switching gain satisfying η ≥ Δ.However,based on Assumption 2,the upper bound Δ remains uncertain in many practical situations.This yields an overestimation of the robust gain η,which contributes to a chattering increase.In addition,applying the discontinuous signum function sign(s)leads to the guidance law being a discontinuous controller,which induces the chattering problem.Therefore,from the above-mentioned contents,in order to circumvent an overestimation of the robust switching control gain,a modified continuous adaptive fast fixed-time NTSM guidance law

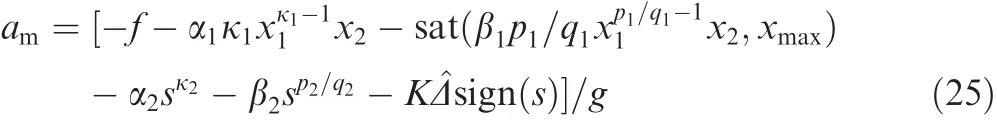
is proposed and updated by

where K≥1.

3.3.Stability analysis

Before verifying the fixed-time convergence of the proposed guidance law in Eq.(25),the following lemmas which play an important role in the analytical process are given.

Lemma 331.For any xi∈ R,where ν∈ （0，1］.If v ≥ 1,we have

Fig.6 Weaving target interception with various desired impact LOS angles under the AFFTNTSMGL proposed by fixed-time stability.

Lemma 429,34.Consider the nonlinear system in Eq.(9).Suppose that there exist a Lyapunov function V(x),scalars a,b,γ1,γ2,k0∈ R+,γ1k0＜ 1,γ2k0＞ 1,and 0＜ Θ ＜ ∞,so that ˙V（x）≤-（aV（x）γ1+aV（x）γ2）k0+Θ.Then,the trajectory of this system is practically fixed-time stable.In addition,the residual set of the solution in Eq.(9)can be given by｛limt→Tx|V（x）≤ min｛a-1/γ1［Θ/（1- φk0）］1/（k0γ1），b-1/γ2［Θ/（1- φk0）］1/（k0γ2）｝｝,where φ is a scalar and satisfies 0＜φ≤1.Moreover,the time needed to reach the residual set is bounded as

Theorem 1.For the guidance system shown in Eq.(7),if the fast fixed-time NTSM manifold is provided by Eq.(20)and the guidance law is selected as Eq.(25)with the adaptive update law designed by Eq.(26),then the variables s and~Δ are all bounded.The trajectory of the closed-loop system will converge to a small neighborhood of the equilibrium point within a bounded finite time T independent on initial conditions.That is to say,the trajectory of the guidance system is practically fixed-time stable,where the settling time T is given by

whereand

Proof.According to choosing Eq.(25)as the control input,the closed-loop system of the fast fixed-time terminal sliding mode dynamics can be transformed into

Consider the following positive definite Lyapunov function:

where=Δ-represents the estimation error of Δ.Then,differentiating V1with respect to time along the trajectory in Eq.(28)yields

where η1=2（κ2+1）/2α2and η2=2（p2/q2+1）/2β2.It can be found that≤0.Therefore,V1(t)≤V1(0)holds,which implies that V1(t)is bounded.So far,we can conclude that the sliding mode manifold s and the estimation error~Δ are all bounded.Due to

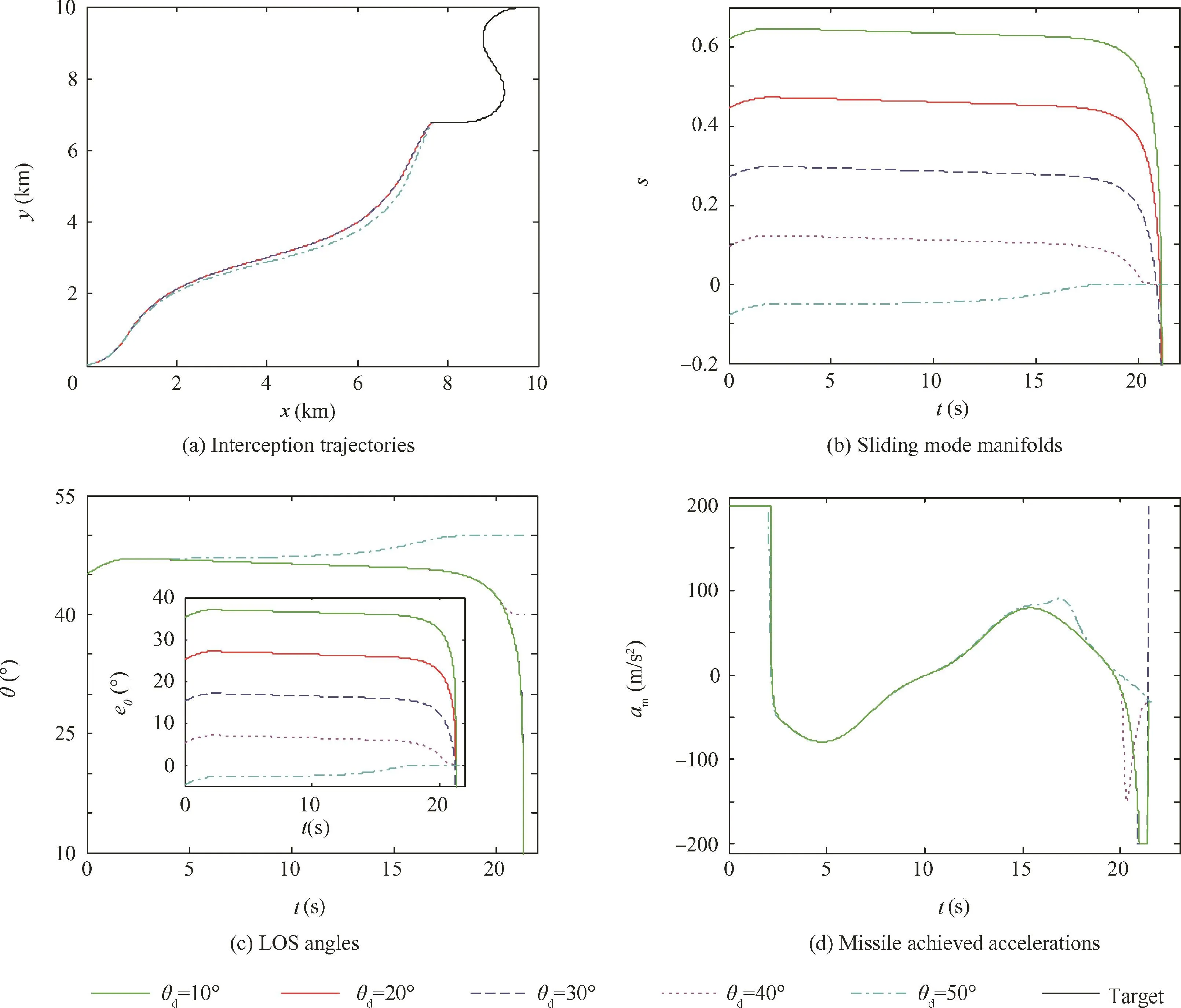
Fig.7 Weaving target interception with various desired impact LOS angles under the NTSMGL proposed by finite-time stability:

κ2≥ 1 and 0 ＜ p2/q2＜ 1,there exist （κ2+1）/2 ≥ 1 and（p2/q2+1）/2 ＜ 1.From Lemma 3,we have

wherewith bounded~Δ.Thus,assume that there exists an unknown constant δ0and a compact set D so thatThen we have

whereFrom Lemma 4,the trajectory of the guidance system in Eq.(7)tends to be practically fixed-time stable.Besides,the residual set D1is calculated as

The settling time is given by T≤1/［η2φ（1-（p2/q2+1）/2）］+2（κ2+1）/2-1/［η1φ（（κ2+1）/2-1）］. Therefore, the proof of Theorem 1 is completed.□

Remark 4.In the proof process, the case whereholds is ignored.The reasons are shown as follows.If we regard the singularity area as the region where inequalityholds,from the first equation in Eq.(7),the solution for state variables can be obtained by

If x2(t)＞0 holds,x1(t)will increase monotonically and leave the singularity area,which is defined as the region where inequalityholds.Similarly,if x2(t)＜0 holds,x1(t)will decrease monotonically and also leave the same singularity area.Both cases demonstrate that the guidance system lies in the singularity region transiently.Therefore,as indicated in Ref.35,the existence of a singularity region cannot influence the result of fixed-time convergence stability analysis.

Theorem 1 is only used to ensure that the variables s and~Δ achieve practical fixed-time convergence.Therefore,propose the next theorem which can guarantee that the proposed sliding manifold s converges to the origin in fixed time while x1and x2converge to the regions near the origin in fixed time.

Fig.8 Target maneuver pro file in Case 2.

Theorem 2.Consider the guidance system in Eq.(7)with the fast fixed time NTSM manifold in Eq.(20).Then applying the control input in Eq.(25)and the adaptive law in Eq.(26),there exist positive constants α1, β1, α2, β2and positive odd integersm1,n1,p1,q1,m2,n2,p2,q2satisfying that m1＞n1,p1＜q1＜2p1,m2＞n2,and p2＜q2while(m1+n1)/2,(p1+q1)/2,(m2+n2)/2,and(p2+q2)/2 being positive odd integers,so that the system states converge to the origin within a fixed-time Tsand the guidance system is fixed-time stable.

Proof.Consider the following Lyapunov candidate function:

Similarly,the time derivative of the Lyapunov function Vscan be obtained as

Sincethere existsfor any t≥0.Since K≥1,Eq.(34)can be rewritten as

Chooselarge enough and K satisfying

Meanwhile,combined withthe following can be obtained:

From Eq.(37),we have

When|s|≥1,one obtains

When|s|＜1,Eq.(38)becomes

According to Lemma 2,Eq.(7)reaches the proposed sliding mode manifold within a bounded time,and the bound of convergence time can be estimated by

When the system reaches the sliding mode manifold s=0,similarly,consider the Lyapunov function Vx1=and the stability analysis of the guidance system states that converge to the small neighborhood of zero is as follows.

The ideal sliding motion of the guidance system satisfies the following equations:

The time derivative of the Lyapunov function Vx1is given by

Based on Lemma 2,the state variable x1is stabilized within a bounded finite time given by

From Eqs.(43)and(44),we can obtain that when the state variable x1enters the region|x1|≤ ε with fast fixed-time convergence,the state variable x2also settles down to the region,i.e.,

Finally,the convergence time for the guidance system in Eq.(7)can be estimated as

Therefore,x1and x2converge to the regions near the origin in fixed time,and Theorem 2 is proven.□

4.Simulations results

Fig.9 Comparison results using different guidance laws for Case 1.

Fig.10 Comparison results using different guidance laws for Case 2.

Fig.11 Weaving target interception with different convergence times under the AFFTNTSMGL.

In order to validate the effectiveness and superiority of the proposed Adaptive Fast Fixed-Time NTSM Guidance Law(AFFTNTSMGL),a surface-to-air interceptor is taken into account in its terminal guidance phase against a maneuvering target,and extensive results of the performance of the proposed guidance law obtained from numerical simulation are presented.From these results,the desired final LOS angle is computed by Eq.(6),and the normal acceleration is obtained and bounded according to Eq.(25)with the adaptive law in Eq.(26).Here,the missile autopilot is considered as the following second-order system,which fully considers that the time lag and autopilot dynamics between the acceleration command and the achieved acceleration always exist:

where amais the real achieved normal acceleration,ξmand ωmrepresent the damping ratio and natural frequency of the interceptor autopilot,respectively.The autopilot parameters are set as ξm=0.8 and ωm=10rad/s.Besides,an airframe is taken as a first-order lag block with a time constant equal to 0.3 s,and the upper bound of the interceptor’s achieved acceleration 20g with g=9.81 m/s2.The initial conditions of the interceptor and the target are listed in Table 1.

In this section,an incoming orthogonal interception by a surface-to-air missile is simulated.Here,we assume perfect knowledge of the range r and the range rate˙r.The missile seeker that measures the LOS angle and the LOS angular rate is taken as a first-order lag system with a time constant of 0.1 s to filter the additive Gaussian measurable noise.Thus,the LOS angular rateθ˙ provided by the seeker from lagged angular information is introduced into the guidance law as the LOS angular rate estimate d^θ/dt.The design parameters for implementing the proposed AFFTNTSMGL are listed in Table 2.

For the purpose of better illustration,the Fixed-Time NTSM Guidance Law(FTNTSMGL)based on the achievements obtained by Zuo32,33,the Fast NTSM Guidance Law(FNTSMGL)proposed by He et al.27,the NTSM Guidance Law(NTSMGL)in Ref.26,and the Finite-Time Guidance Law(FTGL)in Ref.23are employed in simulations,where the FTNTSMGL is given by

wherein which a1,b1＞0.The parameters in Eq.(48)are set as m1/n1=m2/n2=5/3,p1/q1=p2/q2=3/5,a1=b1=1,a2=b2=0.25,xmax=6,η =100，and τ=0.01.From Ref.27,theFNTSMGL is defined as

Fig.12 Sudden target interception with different convergence times under the AFFTNTSMGL.

where e=θ-θd,=,and the sliding mode manifold is designed as s=˙e+μ1e+μ2χ（e）with

where p and q are two positive odd integers satisfying that 1/2＜ p/q ＜ 1, B1= （2-p/q）ϖp/q-1, B2= （p/q-1）ϖp/q-2,and¯s=˙e+μ1e+μ2ep/q.Here,wechoosethesame values of parameters in the FNTSMGL as those given in Ref.27. In addition, the NTSMGL is defined as am=-2˙r˙θ+rκ|˙e|2-a3sign（˙e）/a3+η1tanh（s/τ）with s=e+b3|˙e|a3sign（˙e）,where κ,b3,η1＞0,1＜a3＜2,and the parameters are taken as κ=1,a3=b3=1.5,and η1=400.The FTGL is designedasam=-N˙r˙θ+f0tanh（˙θ/τ）+β0|˙θ|μ0tanh（˙θ/τ）,whereN=3,f0=80,β0=30,and μ0=0.5.Simulation integration is done by the Runge–Kutta method with a time step of 0.01 s.

4.1.Interception with different initial heading angles

In this case,simulations are carried out for interception against weaving targets(targets executing sinusoidal maneuvers)26with different initial heading angles of an interceptor,where the lateral acceleration of a targetis given by at=8gsin(πt/10)m/s2Besides,the desired impact LOS angle is set as 40°,but the initial heading angles of the missile γmare chosen as 30°,60°,90°,120°,and 150°,respectively.To evaluate the performance of the proposed guidance law against a waving maneuver of the target,the proposed fixed-time convergent guidance law is compared with the NTSMGL established on the conventional finite-time theory.

Fig.4 shows the simulation results with differential initial heading angles under the proposed guidance law,and some detailed results related to interceptor-target trajectories,occurrence of sliding modes,tracking of LOS angles,and lateral achieved accelerations are presented in Fig.4,respectively.These can be compared with Fig.5 under the NTSMGL.It can be observed that the settling times for the sliding mode manifold for all the conditions are independent on initial heading angles of the interceptor,i.e.,11 s.Furthermore,the proposed guidance law provides a higher rapid convergence rate for the sliding mode manifold and LOS angle than that of the existing NTSMGL.Therefore,the proposed guidance law achieves fast fixed-time convergence regardless of different initial conditions,and the missile’s normal accelerations are within their maximum allowable limits,i.e.,20g,with no chattering and peak phenomena caused by target maneuver in the terminal phase.The miss distances,impact LOS angles,and interception times obtained by these two different guidance laws under different initial heading angles are summarized inTable 3,which suggest that the proposed guidance law can obtain a more accurate interception performance with a shorter interception time than those of the NTSMGL.

Table 1 Initial parameters for simulation.

Table 2 Parameters of the proposed AFFTNTSMGL.

4.2.Interception with various desired impact LOS angles

In this case,the simulation results of weaving target interception with various desired impact LOS angles are presented.The maneuver acceleration of the weaving target is still taken as at=8gsin(πt/10),and the initial heading angle of the interceptor γmis supposed to be 15°.In contrast to the previous section,the desired impact LOS angles in simulations are selected as 10°,20°,30°,40°,and 50°,respectively.Similarly,we choose the same NTSMGL as the compared method to verify the fixed-time convergence of the proposed guidance law.The results are shown in Figs.6 and 7.Different from the NTSMGL,the sliding mode manifolds and LOS angles θ of the proposed guidance law also converge to the desired values within bounded finite time,which is independent of the desired LOS angles and can be estimated in advance.The missile lateral accelerations respond to the guidance demand rapidly,and still there are no chattering and too large terminal required acceleration in the proposed guidance system.The miss distances,impact LOS angles,and interception times with the AFFTNTSMGL and the NTSMGL under different desired impact LOS angles are shown in Table 4.It is found that,with the existing NTSMGL,the divergence of the terminal impact LOS angle at interception is stimulated by the target maneuver,while the proposed AFFTNTSMGL improves the precision of the miss distance and the desired LOS angle tracking simultaneously,and the settling times for the sliding modes are indeed identical.

Table 3 Miss distances,impact LOS angles,and interception times for weaving target interception with different initial heading angles in Section 4.1.

Table 4 Miss distances,impact LOS angles,and interception times for weaving target interception with different desired impact LOS angles in Section 4.2.

Table 5 Miss distances,impact LOS angles,and interception times for Cases 1 and 2.

Table 6 Miss distances,impact LOS angles,and convergence time estimations for Cases 1 and 2.

4.3.Interception with different target maneuvers

To evaluate the superiority of the proposed guidance law,two different target maneuvers are taken into account.Case 1:The target performs weaving maneuvers as at=8gsin(πt/10).Case 2:The target performs sudden maneuvers as depicted in Fig.8.

In this section,the desired impact LOS angle θdis chosen as 40°,and the initial heading angle of the interceptor is selected as 15°.The simulation results containing the planar interception trajectories,relative range pro files between the interceptor and the target,LOS angle pro files,LOS angular rates,interceptor achieved accelerations,sliding mode manifolds,tracking error pro files of the LOS angle,and the system’s state-plane trajectories,obtained by the AFFTNTSMGL,the FTNTSMGL,the FNTSMGL,the NTSMGL,and the FTGL,are presented in Figs.9–10.Fig.9 are for Case 1,while Fig.11 for Case 2.The miss distances,impact LOS angles,and interception times with these five different guidance laws under the above two cases are presented in Table 5.As described in interception trajectories and relative range pro files,an accurate attack against the maneuvering target is achieved in some sense under these five guidance laws.Fortunately,the miss distance obtained by the proposed AFFTNTSMGL is smaller than those of the other four methods.The reason is that the proposed guidance law provides strong robustness and disturbance rejection by using an adaptive law to estimate unknown bounds of the lumped disturbance.Besides,employing an adaptive robust gain resolves the problem of switch gain overestimation without any knowledge on target maneuvers so that the chattering phenomenon is eliminated,while the other four guidance laws cannot.Therefore,the proposed guidance law is more practical.According to the above simulation results,it is obviously verified that the proposed guidance law offers an interesting fast fixed-time convergence,that is,the settling time can be estimated in advance and is independent of initial state conditions.In this section,we can obtain that the convergence rate of the sliding mode can be adjusted only by changing the parameters of the proposed AFFTNTSMGL,which suggests that the proposed guidance law achieves faster convergence of the sliding mode than those of the other guidance laws,as shown in Fig.9(f)and 10(f).In addition,one can further observe in Fig.9(h)and 10(h)that the performance of the proposed AFFTNTSMGL in driving the tracking errors of the LOS angle and the LOS angular rate to zero is superior to those of the other four guidance laws.Based on the above simulations and analysis,it can be found that the proposed AFFTNTSMGL exhibits better transient,stronger robustness,more precise interception,and better guidance tracking performance than those of the other four guidance laws.As a result,the proposed guidance law has wonderful overall performance and is bene ficial to real implementations.

4.4.Interception with different convergence times

From the above analysis,the AFFTNTSMGL proposed in this paper achieves that the closed-loop system can be stabilized within bounded settling time independent on initial conditions,and the convergence time can be estimated by the design parameters of the AFFTNTSMGL.In order to demonstrate that,simulations of the same initial conditions with different convergence times are needed.From Eq.(46),it can be found that the estimation of the convergence time is related to some design parameters in the AFFTNTSMGL.Here,simulations are executed under different design parameters so that different convergence times can be obtained.

In this section,the desired impact LOS angle θdis chosen as 40°,and the initial heading angle of the interceptor is selected as 15°.Two different target maneuvers,which are the same as those in the above section,are considered.Simulation results containing planar interception trajectories,sliding mode manifolds,LOS angle pro files,and interceptor achieved accelerations obtained by the AFFTNTSMGL are shown in Figs.11 and 12.Fig.11 is for Case 1,and Fig.12 for Case 2.The miss distances,impact LOS angles,and interception times with the aforementioned five different guidance laws under the above two cases are presented in Table 6.From Table 6,it can be found that choosing the design parameters appropriately is in favor of obtaining an accurate impact LOS angle and a rapid convergent speed,which is proven useful as the basis for parameter tuning in the proposed AFFTNTSMGL.

5.Conclusions

A novel smooth adaptive fast fixed-time convergent nonsingular terminal sliding mode guidance law for intercepting a maneuvering target is proposed considering terminal impact angle constrains.In contrast to existing fixed-time or finitetime guidance laws,the proposed guidance law provides a more rapid convergence both far away from and in a close range of the origin,and employs a continuous piecewise function to overcome the singularity problem.Besides,the closedloop guidance system can be stabilized with bounded settling time independent on initial launched conditions and has a higher pointing accuracy with chattering-free achieved accelerations of the interceptor.The performance of the proposed guidance law is inspected through extensive numerical simulations of the planar relative motion equations with the impact angle constraint and compared with some existing fixed-time or finite-time convergent guidance laws.Simulation results present that the proposed guidance law can offer a faster fixed-time convergence rate,a stronger robustness against unknown target maneuvers,and a better interception performance with a higher accuracy and a smaller tracking error of the LOS angle than those of existing guidance laws.In the future,integrated guidance and control design based on the proposed fast fixed-time convergent theory will be investigated.

Acknowledgements

The authors would like to thank the editor and all the anonymous reviewers for their comments,which helped to improve the quality of this paper.This work was supported in part by the National Natural Science Foundation of China(Nos.11202024,11572036).

1.Hou ZW,Liu L,Wang YJ,Fan JH.Terminal impact angle constraint guidance with dual sliding surfaces and model-free target acceleration estimator.IEEE Trans Control Syst Technol 2017;25(1):85–100.

2.Nesline FW,Zarchan P.A new look at classical vs modern homing missile guidance.J Guid Control Dynam 1981;4(1):78–85.

3.Song JH,Song SM,Zhou HB.Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints.Int J Control Autom Syst 2016;14(1):99–114.

4.Harl N,Balakrishnan SN.Impact time and angle guidance with sliding mode control.IEEE Trans Control Syst Technol 2012;20(6):1436–49.

5.Taub I,Shima T.Intercept angle missile guidance under time varying acceleration bounds.J Guid Control Dynam 2013;36(3):686–99.

6.Kumar SR,Rao S,Ghose D.Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints.J Guid Control Dynam 2012;35(4):1230–46.

7.Ratnoo A,Ghose D.Impact angle constrained interception of stationary targets.J Guid Control Dynam 2008;31(6):1817–22.

8.Ratnoo A,Ghose D.Impact angle constrained guidance against nonstationary nonmaneuvering targets.J Guid Control Dynam 2010;33(1):269–75.

9.Cho D,Kim H,Tahk MJ.Impact angle constrained sliding mode guidance against maneuvering target with unknown acceleration.IEEE Trans Aerospace Electron Syst 2015;51(2):1310–23.

10.Xiong SF,Wang WH,Liu XD,Chen ZQ.Guidance law against maneuvering targets with intercept angle constraint.ISA Trans 2014;53(4):1332–42.

11.Wang H,Lin DH,Chen ZX,Wang J.Optimal guidance of extended trajectory shaping.Chin J Aeronaut 2014;27(5):1259–72.

12.Ohlmeyer EJ,Phillips CA.Generalized vector explicit guidance.J Guid Control Dynam 2006;29(2):261–8.

13.Kim BS,Lee JG,Han HS.Biased PNG law for impact with angular constraint.IEEE Trans Aerosp Electron Syst 1998;34(1):277–88.

14.Sang DY,Min BM,Tahk MJ.Impact angle control guidance law using Lyapunov function and PSO method.Proceedings of SICE annual conference;2017 Sept 17-20;Takamatsu,Japan.Piscataway:IEEE Press;2007.p.2253-7.

15.Shtessel YB,Shkolnikov IA,Levant A.Guidance and control of missile interceptor using second-order sliding modes.IEEE Trans Aerosp Electron Syst 2009;45(1):110–24.

16.Zhao Y,Sheng YZ,Liu XD.Sliding mode control based guidance law with impact angle constrain.Chin J Aeronaut 2014;27(1):145–52.

17.Shima T.Intercept-angle guidance.J Guid Control Dynam 2014;27(1):145–52.

18.Lu KF,Xia YQ.Finite-time fault tolerant control for rigid spacecraft with actuator saturations.IET Cont Theory Applicat 2013;7(11):1529–39.

19.Bhat SP,Bernstein DS.Finite-time stability of continuous autonomous systems.SIAM J Control Optim 2000;38(3):751–66.

20.Yu JY,Zhang YA,Gu WJ.Approach to integrated guidance/autopilot design for missiles based on terminal sliding mode control.Proceedings of international conference on machine learning and cybernetics;2004 August 26–29;Shanghai.Piscataway:IEEE Press;2004.p.610–5.

21.Yu JY,Xu Q,Zhi Y.TSM control scheme of integrated guidance/autopilot design for UAV.Proceedings of 3rd international conference on computer research and development;2011 March 11–13;Shanghai.Piscataway:IEEE Press;2011.p.431–5.

22.Zhang Y,Sun M,Chen Z.Finite-time convergence guidance law with impact angle constraint based on sliding-mode control.Nonlinear Dyn 2012;70(1):619–25.

23.Zhou D,Sun S,Teo KL.Guidance laws with finite time convergence.J Guid Control Dynam 2009;32(6):1838–46.

24.Kumar SR,Rao S,Ghose D.Non-singular terminal Sliding Mode Guidance and Control with Terminal Angle Constraints for Non-Maneuvering Targets.Proceeding of the 12th international workshop on variable structure systems;2012 Jan 12–14;Mumbai,Maharashtra.Piscataway:IEEE Press;2012:291–6.

25.Song QZ,Meng XY.Design and simulation of guidance law with angular constraint based on non-singular terminal sliding mode.Physics Procedia 2012;25:1197–204.

26.Kumar SR,Rao S,Ghose D.Nonsingular terminal sliding mode guidance with impact angle constraints.J Guid Control Dynam 2014;37(4):1114–30.

27.He SM,Lin DF,Wang J.Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets.Nonlinear Dyn 2015;81:881–92.

28.Sun LH,Wang WH,Yi R,Xiong SF.A novel guidance law using fast terminal sliding mode control with impact angle constraints.ISA Trans 2016;64:12–23.

29.Polyakov A.Nonlinear feedback design for fixed-time stabilization of linear control systems.IEEE Trans Autom Control 2012;57(8):2106–10.

30.Gao JW,Cai YL.Fixed-time control for spacecraft attitude tracking based on quaternion.Acta Astronaut 2015;115:303–13.

31.Jiang BY,Hu QL,Friswell MI.Fixed-time attitude control for rigid spacecraft with actuator saturation and faults.IEEE Trans Cont Syst Technol 2016;24(5):1–7.

32.Zuo ZY.Nonsingular fixed-time consensus tracking for secondorder multi-agent networks.Automatica 2015;54:305–9.

33.Zuo ZY.Non-singular fixed-time terminal sliding mode control of non-linear systems.IET Control Theory Appl 2015;9(4):545–52.

34.Zhu Z,Xia YQ,Fu M.Attitude stabilization of rigid spacecraft with finite-time convergence.Int J Robust Nonlinear Control 2011;21(6):686–702.

35.Feng Y,Yu XH,Han FL.On nonsingular terminal sliding mode control of nonlinear systems.Automatica 2013;49(6):1715–22.