Dynamic modeling and simulation of a pressurized system used in flight vehicle

Bing SUN,Qi XU,Yang CHEN

School of Astronautics,Beihang University,Beijing 100083,China

1.Introduction

As a part of propulsion system in aerospace flight vehicle,the pressurized system generally involves high-pressure gas vessel,pressure reducing regulator,valve and other attached pipes.By delivering the pressurized gas stored in gas vessel into the propellant tank with designed pressure,the system can control the ullage pressure of propellant tank,and guarantee that the propellant is supplied to engine pump or combustion chamber with designed pressure and flux.

Numerical simulation,as a research approach in addition to experimentation,can shorten design and development time,reduce experimental costs and provide guiding advice for experiments.Many researchers conduct simulations on different pressurized systems.Matsumoto et al.1proposed a new self-pressurized system for propellant feed system so as to reduce the system weight.The steady mathematical model was established and verified to describe the system behavior.Karimi et al.2simulated a pressurized system in upper stage engine.It had a special capsule stored by high-pressure gas.The simulation results proved that the heat exchanger installed in front of the tank can improve the performance of pressurized system.They3also conducted simulation on a warm pressurized system,and a simultaneous simulation approach was verified.Li et al.4studied a pressurized feed system of the dual-thrust hybrid rocket motor.The influences of some structure parameters and initial state parameters on the performance of motor were obtained.Guo et al.5conducted an investigation on a gas cycling test system.The simulation results showed that the refueling gas temperature has a significant effect on the stable temperature.Then they6designed and simulated a new gas cycling test system by using multi-stage storage and self-pressurized method.The simulation results showed that total energy consumption of the system decreases with the increase of gas storage stages.Among these numerical researches,various simplifications and assumptions are adopted.For example,the system nonlinear factors are ignored1;the pressuring gas is considered as ideal gas2,4;the component or system is considered as thermal isolation2;the kinetic energy and potential energy of the flow are ignored2,4;the pipe dynamics is ignored3,4;the state parameters in cavity are considered instantaneously uniform4–6;the transient opening processes of some valves are ignored.4

As an important control component for pressurized system,the pressure reducing regulator can decrease and stabilize the pressurized gas pressure.Since the regulator is a kind of valve,the researches of various valves can be referred to for the study of regulator.Three-dimensional(3D)model7–12is widely applied to simulate different valves.Refs.8–10conduct simulations on the steady flow field which has definite valve spool opening and boundary condition.It is easy to obtain flow field distribution under different opening,structure or boundary condition.Refs.11,12use the dynamic mesh method to calculate the transient flow field with changed opening,and the minimum opening is not zero in order to maintain fluid mesh continuity.Although 3D meshes can model the real structure and 3D model can compute the detailed flow field,they will lead to complex modeling and long-time computing.

The component-level research can use high-dimensional CFD method.However,it does not enable representation of the whole system.13Therefore,the system-level research must reach reasonable balance between accuracy of component modelsand complexity of the overall system. The general approach14is to use the 1D or even 0D simplified model for modeling and simulation,with focus on overall characteristics of the system and the specific role of a single component during the system dynamic change.Many mature system-level simulation tools are developed in this way,such as Amesim,15FloMASTER,16,17EcosimPro,18–20Easy5,21,22GFSSP23,24(Generalized Fluid System Simulation Program),and so on.25–29

Amesim(Advanced modeling environment for performing simulation of engineering systems)was developed by Imagine S.A.in France in 1995 and now belongs to Siemens AG in Germany.It is an open,powerful and user-friendly platform to model,run and analyze complex multi-domain systems and components.15Its new version is LMS Imagine.Lab Amesim 15 released in 2016,and it has 40 libraries and more than 4500 ready-to-use components.FloMASTER,formerly known as Flowmaster,was first released commercially in 1987 by Flowmaster Ltd.in UK and now belongs to Mentor Graphics Corporation in USA.It is a 1D CFD solution for the modeling and analysis of fluid mechanics in complex piping systems of any scale,16and its new version is FloMASTER V8.1 released in 2016.EcosimPro is a modeling and simulation tool for modeling 0D or 1D multidisciplinary continuous discrete systems and any kind of system based on differential-algebraic equations and discrete events.18Its first version is released in 1993,and the latest version is EcosimPro 5.10 released on Dec.18,2017.Easy5 is a graphics-based software tool used to model,simulate,and design multi-domain dynamic systems.21It is developed by MSC (MacNeal-Schwendler Corporation)Software Corporation in USA,and its latest version is Easy5 2017 released in Dec 2016.Method Of Characteristics(MOC)is adopted to calculate the transient flow of gas pipe.22GFSSP has been developed by NASA in USA since 1990s.This software aims to conduct static and dynamic simulation on 1D compressible fluid network.The fluid network is considered as a combination of many nodes and branches.Finite Volume Method(FVM)is used to establish different conservation equations.23This software is still developing in recent years by adding new models and improving algorithm,and the current version is GFSSP Version 701 released in Dec.2015.REDS(Rocket Engine Dynamic Simulator)28has been developed by JAXA(Japan Aerospace Exploration Agency)in Japan since 2001.This program aims to calculate the startup and shutdown transient process of LE-7A rocket engine.Its modeling method is similar with GFSSP.LRETMMSS(Modularization Modeling and Simulation Software for the transients of Liquid Propellant Rocket Engines)29was developed by National University of Defense Technology in China in 2002.It establishes a finite element state-variable model system by employing two kinds of finite volume grids staggered in discrete space.This modeling approach is the staggered-grid FVM essentially.

FVM30derives its discrete equation based on the integral equation in its control volume.The discrete equation expresses the flux equilibrium in control volume,and each term has clear physical meaning.The connection between different components can be managed by FVM easily.It is beneficial to the system-level simulation.With these advantages,FVM will gradually become the mainstream discretization method for establishing large numerical simulation systems.Based on this idea,Ref.31establishes a novel simulation theory and model system for flow/heat transfer/combustion multi- field coupling pipe- flow system.It is a combination of the flow/heat transfer two- field coupling pipe- flow model subsystem,the chemical equilibrium thermodynamic calculation-based and the chemical kinetics-based multi- field coupling subsystems.The applications to some practical engineering systems13,14,31,32have verified its applicability and accuracy.

Whether the regulator can work stably has a crucial effect on the pressurized system.Many researchers carry out related work through system-level simulation.Zafer and Luecke33used root locus method to investigate the stability-sensitivity of some design parameters in the regulator.However,the simulation results are obtained on the basis of linearized model and cannot reflect the oscillation directly.Rami et al.34studied the influences of structure and control parameters on the regulator stability by the time-domain transient simulation.Among the system-level dynamic models for miscellaneous valves35–38and regulators,33,34,39,40the main distinction is complexity.Some simulations use adiabatic model,33,35–37linear model33or isothermal model,40and these models do not strictly agree with the real situation.Some models ignore the pneumatic forces provided by different cavities or moving parts,33,40or use pressure difference-based injector orifice model33,34to compute the flux of valve spool or orifice.

In light of the advantages and disadvantages of various valve models,starting from the flow/heat transfer two- field coupling pipe- flow model subsystem,31a system-level model of a novel Dual-Stage Gas Pressure Reducing Regulator(DSGPRR)is established.The variation of cavity volume,the movement of valve spool,and heat transfer of wall are considered.Then the dynamic model of a pressurized system used in flight vehicle is established to simulate the working characteristics of the system and the specific role of each component.Based on these,the influences of various structure parameters on the DSGPRR stability are analysed by a series of simulations,and their variable ranges which can guarantee the stability of DSGPRR are obtained.

2.Physical model of experimental system

Fig.1 shows the schematic diagram of the pressurized experiment system.It includes gas source C0,hand valves C1 and C5,gas vessel C2,solenoid valve C3,DSGPRR C4,orifice C6 and attached pipes.Three pressure sensors are installed at the upstream and downstream pipes of the DSGPRR respectively.The pressure sensor M0 is used to monitor the pressure of C2.The variable pressures of C4 inlet and outlet in whole working period can be obtained through the pressure sensors M1 and M2 respectively.The type of C1 and C5 is ZF5704.4Z,and the nominal pressure is 40 MPa;the type of C3 is K0512410,and its nominal pressure is 45 MPa;the type of M0-M2 is BLD,their accuracy class is 0.25,the measurement range of M0 and M1 is 0–40 MPa,and the range of M2 is 0–2.5 MPa.

Fig.1 Schematic diagram of pressurized experiment system.

Before the startup of test,C1 and C3 are closed;C5 is full-opening;the two valve spools in C4 are full-opening;high-pressure air is stored in C0.Firstly,C1 is opened,and then the high-pressure air in C0 flows into C2.When the pressure monitored by M0 reaches to the design value,C1 is closed and the test preparation is accomplished.

The instantaneous open of C3 marks the startup of experiment.Then the high-pressure air in C2 impinges on C3,and the pressure of each cavity in C4 increases and the openings of two C4 spools decrease.The flux of air ejected by C6 increases.After a short time,the upstream air pressure is reduced and stabilized by C4,and the air is ejected with rated pressure and flux through C6.The air in C2 flows out continuously with system working.After a long working time,the pressure of C2 decreases to the design output pressure of C4.Two C4 spools open gradually until their openings reach maximum.As the upstream pressure continues to decrease,the output air flux cannot be maintained although the two C4 spools are full-opening,so the output air flux decreases continuously.Finally,the pressures of C2-C6 reach to atmospheric pressure and the air in system no longer flows out.The system working process can be divided into five stages from the perspective of pressurized gas feeding:(A)the initial none- flow stage before C3 opens;(B)the increasing- flow stage between the time when C3 opens and the time when the C4 spools reach to rated opening;(C)the steady- flow stage as the C4 spools are in rated openings;(D)the decreasing- flow stage after the C4 spools reach to full-opening again;(E)the final none- flow stage after the C2-C6 pressures decrease to atmospheric pressure.

3.Modeling approach

3.1.Primary governing equations

Based on the integral conservation equations in Eulerian type of specification suitable for control volume of continuous fluid medium,the integral conservative equations of quasi onedimensional compressible transient flow in variable-crosssection pipe can be obtained on condition that the inner heat source is zero as follows:

Above equations can consider pipe-wall elastic deformation,variable fluid properties,gravitational field,friction,axial heat conduction,and the heat transfer between fluid and pipewall.When the volume of the control volume is variable(for example,a certain part of wall of the fluid cavity is a mobile piston),the physical meaning of the elastic deformation term in energy equation is the expansion work exported by fluid.

According to the FVM which has two kinds of finite volume grids staggered in discrete space,13a finite volume model in form of ordinary differential equations can be obtained as follows:

In the equations,andThe boundary parameters of state element can adopt different schemes,and the upwind scheme is used generally.fλ,jis calculated by specific formula according to Reynolds number.13

The transient unsteady heat-conduction differential equation in axisymmetric cylindrical coordinates can be described as follows:

The axisymmetric two-dimensional heat-transfer model which has the form of ordinary differential equation through spatial discretization13can be established as follows:

Based on Eqs.(2)and(4),the transient characteristics of the component which is similar with pipe or volume can be simulated.

The components such as valve,orifice and pressure reducing regulator,have throttling phenomenon.The valve spool and orifice throttling model should be established to calculate the mass flow rate.The general pressure ratio-based injector orifice model can be described as follows:

where Cdrepresents the throttling characteristic and its value can be obtained through test or relation formula.14

On the basis of above primary governing equations, flow and heat transfer can be described.

Table 1 Modularization disassembly of pressurized system.

3.2.Modularization modeling approach

The conventional modeling method usually embeds system constitution and structure into computer program during establishing the model of a system.It means that the program codes must be modified if the system structure changes.The modularization method32can solved this problem effectively.Table 1 shows the module information of five typical components after modularization disassembly of the pressurized system.Fluid source,gas pipe,gas volume and gas valve are four basic modules,and DSGPRR is a module obtained by combinative development from some basic modules.

The models of four basic modules are provided by Ref.13.Below establishes the numerical model of DSGPRR.

3.3.Numerical model of DSGPRR

The function of pressure reducing regulator is to reduce and stabilize the gas pressure to the designed value.Its principle is throttling as high-pressure-cavity gas flows into lowpressure cavity through the narrow channel which is formed by valve spool and valve seat.The pressure energy of highpressure-cavity gas turns to the kinetic energy during flowing through channel,and then turns to the intermolecular potential energy.Subsequently,the pressure of gas decreases as it flows into low-pressure cavity.Fig.2 shows the structure of the DSGPRR used in the pressurized system.It is a dual-stage series redundancy high-pressure unloading diaphragm pressure regulator.Its function is to solve the single point failure produced by single-stage pressure regulator,and enhance the stability of gas system.

Fig.2 Schematic diagram of DSGPRR structure.

Fig.3 Finite control volume grids of DSGPRR.

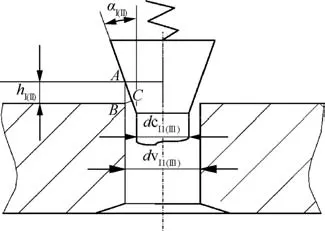
Fig.4 Schematic diagram of throttling at valve spool.

Fig.3 shows the finite control volume grids of the DSGPRR.The grids are built according to the regulator structure by FVM,and its boundaries should be linked to gas pipes.The pressures of I-stage and II-stage spring cavities are equal to the atmospheric pressure due to the wall through holes connected with the external environment,so the two cavities are not involved in the grids.The regulator is divided into 6 cavities including I-stage high-pressure cavity,I-stage feedback cavity,I-stage low-pressure cavity(II-stage high-pressure cavity),II-stage feedback cavity,II-stage deputy feedback cavity and II-stage low-pressure cavity,which are connected by throttling channels.Every cavity should be considered with variable volume because of the movement of spools.Fig.4 shows the schematic of throttling at valve spool when its opening is h.The valve-spool shape of the regulator is tapered.The crosssectional area of throttling channel is the lateral area of a circular truncated cone formed by the line segment BC rotating a circle around the spool axis.According to the geometry,the calculation equations of the area can be developed,and the calculation equations of various cavity volumes and pneumatic acting areas can also be deduced.

The model of the DSGPRR is a combination and expansion of gas-volume model and gas-valve model,and is derived from Eqs.(2)and(5).The model can consider the variation of cavity volume,the movement of spool,and heat transfer of wall.The pressure,density and total energy per unit volume of each cavity are considered instantaneously homogeneous.The positive direction of force is considered as the direction along which the valve spool can be lifted.When the axial heat conduction and the gravity are ignored,the equations of the DSGPRR are obtained as follows:

(1)I-stage valve spool

Cross-sectional area of flow equation:

where CdI1represents spool throttling characteristic and its value is the function of h1.The CdI1-h1curves need to be established for different kinds of spools by test and appropriately amended for different fluid media according to viscosity and density.

(2)I-stage feedback hole

where CdI3represents throttling characteristic of the hole.In the case of reverse flow,that is,when the equation meets 0≤pI2＜pI3,the positions of pI3and pI2are exchanged and a minus sign is added in front of the mass flow rate equation.

(3)I-stage high-pressure cavity

Energy equation:

Volume differential equation:

Volume algebraic equation:

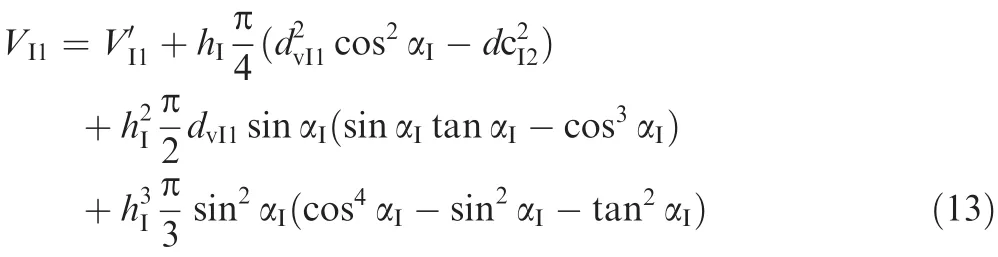
(4)I-stage low-pressure cavity (II-stage high-pressure cavity)

Continuity equation:

Energy equation:

The boundary parameters in Eq.(15)use upwind scheme,such as:when QmI1≥0,pinI21=pI1;when QmI1＜0,pinI21=pI2.

(5)I-stage feedback cavity

(6)I-stage valve spool movement

Force equilibrium equation:

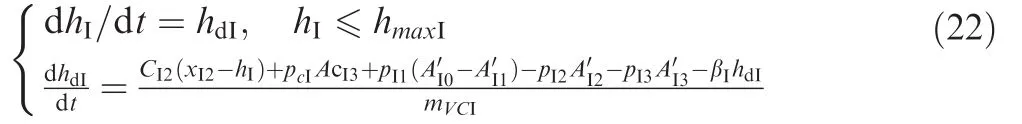
where the effective acting areas are calculated by

(7)II-stage valve spool

Volume differential equation:

Volume algebraic equation:

where CdII1can be obtained by the method same as CdI1.

(8)II-stage feedback hole

The computation method of CdII3is the same as that of CdI3.In the case of reverse flow,the treating method is the same as Eq.(8).

(9)II-stage feedback middle spool

Cross-sectional area of flow equation:

The value of dvII4is considered as dII4.In the case of reverse flow,the treating method is the same as Eq.(8).

(10)II-stage low-pressure cavity

Continuity equation:

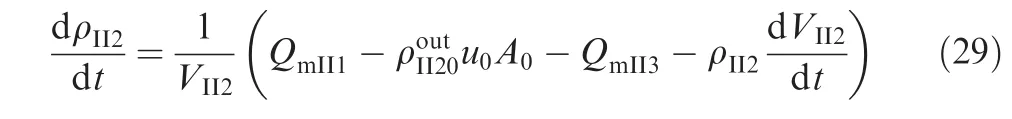
Energy equation:

Volume differential equation:

Volume algebraic equation:

The boundary parameters in Eq.(30)use upwind scheme,and the treating method is the same as Eq.(15).

(11)II-stage feedback cavity

Energy equation:

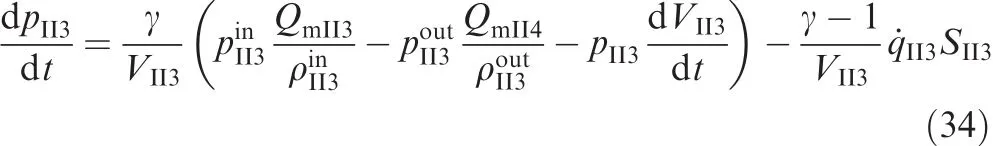
Volume differential equation:

Volume algebraic equation:

(12)II-stage deputy feedback cavity

Continuity equation:

Energy equation:

Volume differential equation:

Volume algebraic equation:

(13)II-stage valve spool movement

Force equilibrium equation:

where the effective acting areas are calculated by

4.Numerical model of experiment system

Fig.5 Numerical simulation model of pressurized system.

Table 2 System initial,structure and control parameters.

The modularization numerical model of the pressurized system is shown in Fig.5.The gas source C0 and the hand valve C1 are omitted.The numerical model system is divided into 1 gas volume(GVol1),5 gas pipes(GP1-5),3 gas valve(GV1-3),1 dual-stage gas pressure reducing regulator(DSGPRR1)and 1 fluid source(FS1).The length,inner diameter and thickness(unit:mm)of each pipe are shown in Fig.5.The flow field grids of every gas pipe are divided by 100 mm/grid.The length along flow direction of the lumped parameter components(such as gas volume,gas valve,etc.)is two standard grid units,i.e.200 mm.The gas is considered as ideal gas.The quasi one-dimensional compressible transient pipe flow model is used to compute gas flow.The pipe-wall radial-direction one-dimensional heat transfer model is used to calculate the wall temperature fields of GP,GV and DSGPRR components.The GVol1 uses the wall zerodimensional heat transfer model.The pipe-wall radial direction grid sequence numbers of the components using 1D heat transfer model total 4.The external surface of each component is natural convection,and the heat transfer coefficient is 5 W/(m2·K).The throttling in GV1 and GV2 use the pressure ratio-based dual-model solution and the local loss model14respectively,and the flow coefficient of GV1 is calculated by the variable-coefficient default formula scheme.14GV3 adopts the pressure ratio-based injector orifice model to simulate its throttling,and its flow coefficient is viewed as constant.CdI1and CdII1are calculated by the variablecoefficient default formula scheme;CdI3,CdII3and CdII4are considered as constant.The wall material of each component is stainless steel,and its thermophysical parameters are constant.The dynamic process of the system is simulated by using the classical four-order Runge-Kutta method.

Fig.6 Comparison of simulation results with test data.

The initial state parameters of the system are shown in Table 2.The air pressure between the GVol1 and the upstream cavity of GV1 is p0;the air pressure between the downstream cavity of GV1 and the upstream cavity of GV2 is p1;the air pressure after the downstream cavity of GV2 is p2;the atmospheric pressure is patm.The temperature of whole pipeline is T0.The volume of GVol1 is V0G.The structure and control parameters are also shown in Table 2.

5.Results and discussion

Fig.6 provides the comparison of the simulation results with the experimental data.The locations of two pressure sensors M1 and M2 are shown in Fig.1,and they represent the pressure of I-stage high-pressure cavity and II-stage low-pressure cavity respectively.The data acquisition frequency of each pressure sensor is 200 Hz,i.e.,a data point per 5 ms.The data output frequency of simulation results is 20 Hz before 1 s;200 Hz during 1–50 s;20 Hz after 50 s.The simulation results and experimental data at four working stages are compared,i.e.,whole working stage(0–1044 s),start-up stage of GV1(1.3–1.8 s),pressure build-up stage of DSGPRR1(0–10 s),and early rated working stage(0–50 s).

Fig.7 Pressure,temperature and mass flow rate of GVol1.

The pressurized system is at initial state and the pressure of each cavity in DSGPRR1 is 0.101325 MPa before 1.4 s.These phenomena are reflected by the simulation and experimental curves in Fig.6(b)and(c).The pressure of each cavity in DSGPRR1 increases rapidly with the opening of GV1 during 1.4–1.6 s as shown in Fig.6(b).The simulation and experimental curves in Fig.6(b)indicate that pI1increases firstly and then becomes relatively steady after a period of oscillations,and pII2decreases to steady state gradually after a peak.The experimental curves show that pII2reaches maximum and steady state prior to pI1,but the simulation curves show there is no apparent difference between them.The comparison of simulation and experiment in Fig.6(b)shows that the simulated curve of pI1rises faster than the corresponding experimental curve and has more obvious oscillation,but their peak and steady values are almost the same;the simulated curve of pII2rises slower than the experimental curve and has slight oscillation in the decreasing stage,but their peak and steady values are also almost the same.

Fig.8 Pressure,temperature and mass flow rate of GV1.

As shown in Fig.6(a),(c)and(d),two valve spools move to the rated state and steady pressure is outputted by DSGPRR1 after the drastic change period of 1.4–1.8 s.There are three differences between simulation results and test data:(A)Fig.6(a)shows that the experimental curve of pI1declines faster than the simulation curve;(B)Fig.6(d)shows that the experimental curve of pI1has a ’bump’in the period of 3–25 s,i.e.,it rises firstly and then declines,but the simulation curve declines continuously with an approximate constant rate;(C)similar with the experimental curve of pI1,the experimental curve of pII2also has a ‘bump’as shown in Fig.6(a),it declines slightly in the period of 1.7–30 s,rises slightly in the period of 30–450 s,and then continues to decline with small amplitudes,but the simulation curve experiences a slight rise in the whole period.The simulated curves agree with the experimental curves in quality,and the numerical errors between them are tolerated in engineering.

The differences between the simulation results and the test data are caused possibly by the following reasons:(A)the air is considered as ideal,and it makes the simulated initial air mass in the gas vessel larger than the real experimental value,so the experimental curve of pI1declines faster than the simulation curve;(B)the pressure sensors are installed at bypass,and it makes the experimental curve more smooth in the start-up stage;(C)the real opening variation curve of GV1 is not measured during experiment,so there is a little error between the simulation and the experiment in the start-up stage;(D)the regulator has some defects in manufacture and assembly,which makes the experimental opening variations of spools deviate from the theoretical situations,so the experimental curves show ‘bump’.

Fig.9 Pressure,opening,moving velocity and mass flow rate of DSGPRR1 in start-up stage.

Fig.10 Pressure,opening and mass flow rate of DSGPRR1 in pressure build-up stage.

The following methods can be used to improve the accuracy of simulation results:(A)the real-gas calculation model should be used to decrease the error caused by ideal gas assumption;(B)the displacement sensor should be installed at the solenoid valve GV1 to measure the real opening variation;(C)the pressure sensor and the displacement(or acceleration)sensors should be installed at the I-stage low-pressure cavity and the spools,respectively,to verify the simulation results more comprehensively;(D)the manufacture and assembly quality of the regulator should be enhanced to decrease the experiment error.

Figs.7–13 show the simulation results of the 11-component numerical system.The dynamic characteristics of GVol1 and GV1-3 are shown in Figs.7,8,12 and 13,respectively.The dynamic characteristics in each period of DSGPRR1 are shown in Figs.9–11.The 1400 s is chosen as the simulationend time because the GVol1 pressure decreases to atmospheric pressure around 1360 s.

It can be seen from Figs.7–13 that the whole system maintains its initial state before 1.4 s.The pressure of the pipeline from GVol1 to GV1 upstream cavity is 35 MPa,the pressure of the pipeline after GV1 downstream cavity is 0.101325 MPa,and the temperature of the whole pipeline is 285.15 K.Fig.9 shows that the pressure of each cavity in DSGPRR1 is 0.101325 MPa,and I-stage and II-stage valve spools are full-opening,i.e.0.5 mm and 0.55 mm respectively.

As shown in Fig.9(a)and(b),the pressure of each DSGPRR1 cavity increases rapidly with GV1 opening in 1.4–1.62 s.As I-stage and II-stage feedback holes have large equivalent diameter,pI3,pII3,pI2and pII2rapidly increase simultaneously.As the initial flow area of II-stage feedback middle spool is zero,and the volume of II-stage deputy feedback cavity is inverse proportional to hII,pII4increases more slowly than pII3.Since the effective acting area of the feedback-cavity gas on spool moving parts is larger than those of other cavities,the movements of two spools are controlled mainly by the pressure of feedback cavities(including II-stage deputy feedback cavity).Therefore,hIand hIIdecrease to rated values from full-opening position mainly with pI3,pII3and pII4changing as shown in Fig.9(c)and(d).After a drastic variation process in the period of 1.4–1.8 s,the two spools stabilize at the rated openings and the regulator begins to output the air with stable pressure and flux.

Fig.11 Pressure,opening,temperature and mass flow rate of DSGPRR1.

As shown in Figs.10 and 11,in the rated working stage,pI1decreases gradually with the consumption of the air in GVol1(Fig.7),and pI2and pII2stabilize approximatively at the rated values.There is a slow rising trend for the pressure curves of pI2(i.e.pII1)and pII2as shown in Fig.11(a)and(b),and Fig.11(b)indicates that the relative rising amplitude of pII2is much less than pI2.The force on spool moving part produced by the pressure of high-pressure cavity makes the spool move to its closed position,so hIincreases with the slash decrease of pI1and hIIdecreases slightly with the increase of pII1.Figs.7,8,11(c)and(d),12,and 13 show that the air temperatures of the whole pipeline decrease continuously with the out flow of air.As the pressures of two DSGPRR1 low-pressure cavities are approximate constant,the densities of DSGPRR1 lowpressure cavities increase gradually.Therefore,QmI1and QmII1calculated by the injector orifice model increase slowly as shown in Fig.11(e)and(f).

Fig.12 Pressure,temperature and mass flow rate of GV2.

Fig.13 Pressure,temperature and mass flow rate of GV3.

When the simulation time reaches to about 1155 s,Fig.11(a)depicts that hIincreases to nearly maximum and the I-stage output pressure of regulator(pI2)begins to decrease due to the decrease of upstream air pressure.Around 1265 s,Fig.11(b)shows that hIIincreases to nearly maximum and the II-stage output pressure(pII2)begins to decrease.In addition,QmI1and QmII1also begin to decrease as shown in Fig.11(e)and(f).Since then,the air outputted by the regulator no longer has rated pressure and flux.Figs.7,8,11(a)and(b),12,and 13 show that the pressures of the whole pipeline reach to atmospheric pressure and the air in the gas vessel is almost completely exhausted around 1360 s.According to Fig.11(c)and(d),as the air flux decreases,the warming effect produced by external environment and pipe wall begins to become significant.The temperature curves of DSGPRR1 cavities present a rising trend after 1300 s,and this phenomenon can also be seen in Figs.7,8,12 and 13.

According to Fig.13,in the rated working stage,the air pressure drops to about 0.1 MPa from 0.65 MPa due to the throttling of GV3.The air mass flow rate curve herein has a slight rising trend,but its value stabilizes at 4 g/s approximatively.It can be seen by referring to Fig.11(a)and(b),due to the superior dynamic performance of the DSGPRR,the output pressure of regulator(pII2)stabilizes around the design value(0.65 MPa),although there is a slight rising trend at its curve and the I-stage output pressure of regulator(pI2,pII1)has a relative obvious rise with the slash decrease of pI1.

In conclusion,the regulator works stably when upstream pressure decreases from 35 MPa to 4 MPa.The output pressure of regulator can be stabilized at its design value(0.65 MPa)within a relative variation range of-0.015%～+0.092%,and the I-stage output pressure of regulator can also be stabilized at its design value(3.2 MPa)within a relative variation range of+0.053%～+2.95%.This type of DSGPRR has excellent output performance,and can provide stable working gas for downstream system.

6.Stability analysis of DSGPRR

In order to make the output pressure of pressure reducing regulator satisfy the design requirement,it is necessary to keep the regulator in a stable working state,i.e.,to maintain the output pressure within the design range without drastic oscillation.By selecting the simulation case in Table 2 as standard case,a series of cases in which each structure parameter changes separately are simulated to study its influence on regulator stability.The sample variance of valve spool opening hIor hIIis selected as stability index,and its value is inversely proportional to the regulator stability.This index considers relative oscillation amplitude and oscillation frequency,and is calculated by

where xiis the value of the ithsample;E(x)is the sample expectation;n is the sample number.The 5–10 s sample time range is chosen to consider the rated working stage,and 1.3×10-6is selected as critical stability value.If the stability index is bigger than the critical value,the regulator is viewed as unstable.The stability indexes of hIand hIIin standard case are 4.28×10-8and 6.27×10-10,respectively.

Fig.14 shows the opening of I-stage and II-stage valve spools in the rated working stage when mVCIis 200 g.The hIcurve has an obvious high-frequency oscillation,and the hIIcurve is stable.In this case,the stability index of hIand hIIare 1.55×10-6and 6.83×10-10,respectively.The regulator is viewed as unstable although the output pressure is stable.As shown in Fig.15,when the value of mVCIdecreases to the half of design value,the stability index of hIand hIIare 4.25×10-8and 6.22×10-10,respectively.The regulator is more stable in this case.

Based on the above judgement criterion,the influences of structure parameters on regulator stability are revealed by a series of simulations.Table 3 gives the stability variation rules and reasonable value ranges of various structure parameters.The design values and calculation ranges are also provided in Table 3.The symbol ‘↑” or ‘↓” means that the stability of this type of regulator will be enhanced or weakened with the change of corresponding structure parameter.

As shown in Table 3,stability variation rules for most structure parameters are monotonous,but the five structure parameters including lI2,dvI3,αI,dvI1and lII4have different variation rules.The stability indexes increase no matter how the values of the above five parameters change.For the parameter lI2,the stability index increases with the increase of this parameter,but its value is always smaller than the critical value,so the corresponding stability value range has no upper limit in the calculation range.For the parameters dvI3and lII4,the stability indexes are always smaller than the critical value,so any value in the calculation range can meet the design requirement.

In addition,the simulation researches indicate that the stability of the DSGPRR is directly related to the II-stage structure parameters.This means that if there is an obvious instability in the I-stage part,the II-stage structure parameters can be improved to ensure that the output pressure meets the design requirement.However,if there is an obvious instability in the II-stage part,it is insignificant to change the I-stage structure parameters.

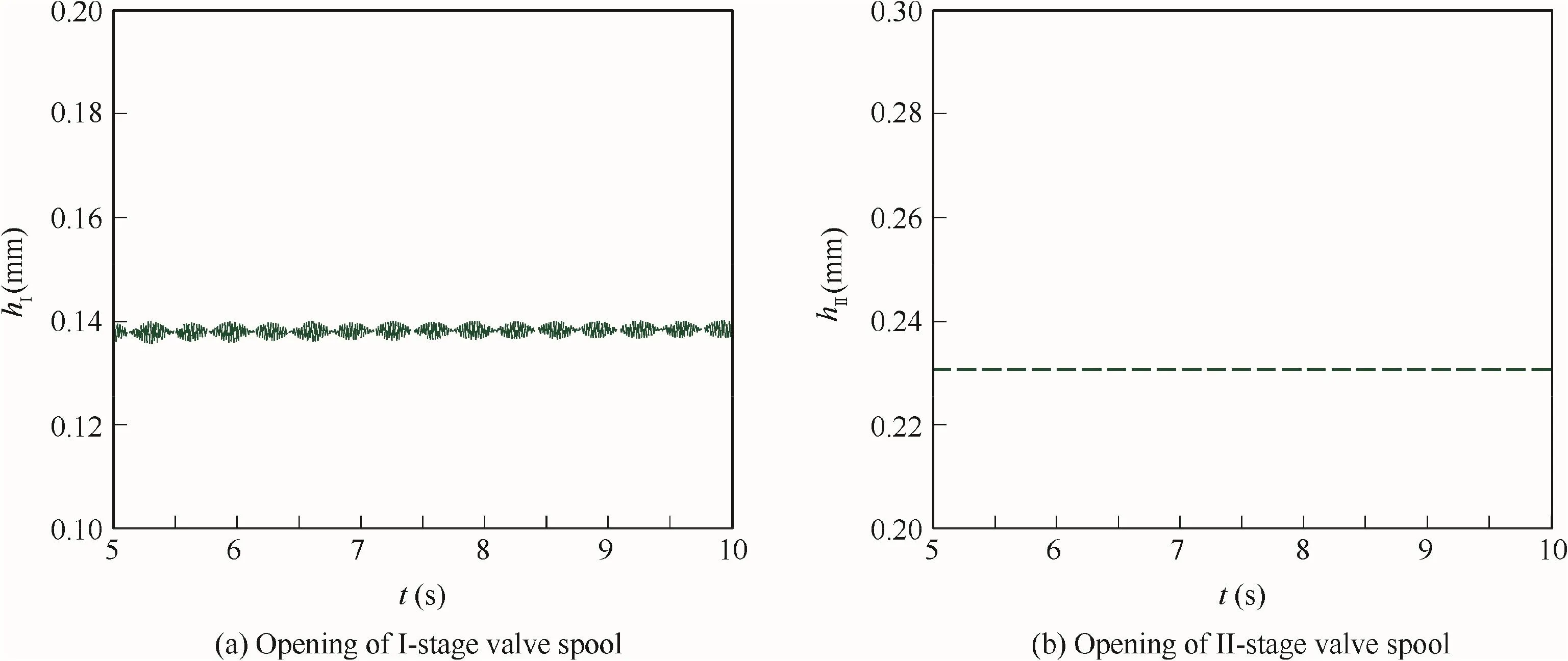
Fig.14 Opening of valve spools when mVCIis 200 g.

Fig.15 Opening of valve spools when mVCIis 16.8105 g.

7.Conclusions

Through the simulation study of the pressurized system,the following conclusions can be obtained:

(1)The system-level numerical models established for the DSGPRR and the system are reasonable and reliable.The simulation results accord well with the experimental data.

(2)As the key component in the system,the DSGPRR has excellent dynamic output performance and can provide stable working gas of 0.65 MPa within a relative variation range of-0.015%–+0.092%.

(3)The DSGPRR stability variation rules for various structure parameters are revealed by a large number of simulations,and the stable value ranges of various structure parameters are also provided.These provide numerical support for the design and improvement of this type of regulator.

(4)The stability of the DSGPRR is directly related to the II-stage structure parameters.The II-stage structure parameters can be improved to ensure the output pressure if the I-stage part has obvious instability,but not vice versa.

(5)For obtaining better simulation results,the real gas effect needs to be considered and the operating time sequence of solenoid valve should be measured.For the more accurate experimental data,additional sensors need to be installed,and the manufacture and assembly precision of regulator needs to be improved.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China(No.11101023)and the China Scholarship Council(No.201203070237).

1.Matsumoto J,Okaya S,Igoh H,Kawaguchi J.Concept of a self pressurized feed system for liquid rocket engines and its fundamental experiment results.Acta Astronaut 2017;133:166–76.

2.Karimi H,Nassirharand A,Nohseni M.Modeling and simulation of a class of liquid propellant engine pressurization systems.Acta Astronaut 2010;66:539–49.

3.Karimi H,Nassirharand A,Zanj A.Integration of modeling and simulation of warm pressurization and feed systems of liquid propulsion systems.Acta Astronaut 2011;69:258–65.

4.Li JH,Yu NJ,Zeng P,Cai GB.Design and integrated simulation of a pressurized feed system of the dual-thrust hybrid rocket motor.Sci China-Technol Sci 2013;56(4):989–1000.

5.Guo JX,Yang J,Zhao YZ,Pan XM,Zhang LF,Zhao L,et al.Investigations on temperature variation within a type III cylinder during the hydrogen gas cycling test.Int J Hydrog Energy 2014;39(25):13926–34.

6.Guo JX,Xing LJ,Hua ZL,Gu CH,Zheng JY.Optimization of compressed hydrogen gas cycling test system based on multi-stage storage and self-pressurized method.Int J Hydrog Energy 2016;41(36):16306–15.

7.Zen W,Tong ZZ,Li SJ,Li HZ,Zhang L.Thermodynamic characteristic study of a high-temperature flow-rate control valve for fuel supply of scramjet engines.Chin J Aeronaut 2012;25(4):559–65.

8.Xu H,Guang ZM,Qi YY.Hydrodynamic characterization and optimization of contra-push check valve by numerical simulation.Ann Nucl Energy 2011;38(6):1427–37.

9.Li BR,Gao LL,Yang G.Evaluation and compensation of steady gas flow force on the high-pressure electro-pneumatic servo valve direct-driven by voice coilmotor.Energy Conv Manage 2013;67:92–102.

10.Zeng LF,Liu GW,Mao JR,Wang SS,Yuan Q,Yuan H,et al.Flow-induced vibration and noise in control valve.Proc Inst Mech Eng Part C-J Eng Mech Eng Sci 2015;229(18):3368–77.

11.Beune A,Kuerten JGM,Van Heumen MPC.CFD analysis with fluid-structure interaction of opening high-pressure safety valves.Comput Fluids 2012;64:108–16.

12.Yonezawa K,Ogawa R,Ogi K,Takino T,Tsujimoto Y,Endo T,et al.Flow-induced vibration of a steam control valve.J Fluids Struct 2012;35:76–88.

13.Chen Y,Wang HS,Xia JX,Cai GB,Zhang ZP.Dynamic modeling and simulation of an integral bipropellant propulsion double-valve combined test system. Acta Astronaut 2017;133:346–74.

14.Chen Y,Cai GB,Zhang ZP,Huang YL.Multi- field coupling dynamic modeling and simulation of turbine test rig gas system.Simul Model Pract Theory 2014;44:95–118.

15.LMS Imagine S.A.AMESim reference manual rev 10;2010.

16.Atmaca AU,Erek A,Altay HM.Comparison of two numerical approaches to the domestic hot water circuit in a combi boiler appliance.Energy Build 2016;127:1043–56.

17.Cai HK,Qian YY,Hou L,Wang WW,Zhang EL,Yang WP.Virtual design and analysis with multi-dimension coupling for engineering machinery cooling system.Sci China-Technol Sci 2015;58(1):117–22.

18.Leonardi M,Nasuti F,Di Matteo F,Steelant J.A methodology to study the possible occurrence of chugging in liquid rocket engines during transient start-up.Acta Astronaut 2017;139:344–56.

19.Lagier B,Hoa C,Rousset B.Validation of an EcosimPro®model for the assessment of two heat load smoothing strategies in the HELIOS experiment.Cryogenics 2014;62:60–70.

20.Zamarren˜o JM,Mazaeda R,Caminero JA,Rivero AJ.A new plug-in for the creation of OPC servers based on EcosimPro©simulation software.Simul Model Pract Theory 2014;40:86–94.

21.Xiao Q,Li QH,Chang C.The influence of lateral shock absorber valve parameters on vehicle dynamic performance.J Mech Sci Technol 2015;29(5):1907–11.

22.MSC Software Corporation.EASY5 2010 gas dynamics library user guide;2010.

23.Majumdar AK,LeClair AC,Moore R,Schallhorn PA.Generalized fluid system simulation program,version 6.0.Washington,D.C.:NASA;2016.Report No.:NASA/TP-2016-218218.

24.Majumdar A,Valenzuela J,LeClair A,Moder J.Numerical modeling of self-pressurization and pressure control by a thermodynamic vent system in a cryogenic tank. Cryogenics 2016;74:113–22.

25.Ramamurthy B,Horowitz E,Fragola JR.Physical simulation in space launcher engine risk assessment.2010 proceedings–annual reliability and maintainability symposium(RAMS);2010 Jan 25–28;San Jose,CA,USA.New York:IEEE;2010.

26.Calabro M,Talbot C.New upper stage propulsion concept for future launchers.Acta Astronaut 2008;63:357–66.

27.Iannetti A,Palerm S,Marzat J,Piet-Lahanier H,Ordonneau G.HMS developments for the rocket engine demonstrator Mascotte.Reston:AIAA;2015.Report No.:AIAA-2015-3992.

28.Yamanishi N,Kimura T,Takahashi M,Okita K,Negishi H,Atsumi M.Transient analysis of the LE-7A rocket engine using the rocket engine dynamic simulator(REDS).Reston:AIAA;2004.Report No.:AIAA-2004-3850.

29.Zhang YL,Liu K,Cheng MS.Dynamics theory and application of liquid propellant rocket engine.Beijing:Science Press;2005[Chinese].

30.Versteeg HK,Malalasekera W.An introduction to computational fluid dynamics:the finite volume method.2nd ed.New Jersey:Prentice Hall;2007.

31.Chen Y,Jiang F,Cai GB,Xu X.A novel simulation theory and model system for multi- field coupling pipe- flow system.Combust Theor Model 2017;21(5):799–837.

32.Chen Y,Cai GB,Wu Z.Modularization modeling and simulation of turbine test rig main test system.Appl Math Model 2011;35:5382–99.

33.Zafer N,Luecke GR.Stability of gas pressure regulators.Appl Math Model 2008;32(1):61–82.

34.Rami EG,Jean-Jacques B,Bruno D,Francois M.Modelling of a pressure regulator.Int J Pressure Vessels Pip 2007;84(84):234–43.

35.Paul BH,Gonthier KA.Analysis of gas-dynamic effects in explosively actuated valves.J Propul Power 2010;26(3):479–96.

36.Ye QF,Chen JP.Dynamic analysis of a pilot-operated two-stage solenoid valve used in pneumatic system.Simul Model Pract Theory 2009;17(5):794–816.

37.Hos CJ,Champneys AR,Paul K,McNeely M.Dynamic behavior of direct spring loaded pressure relief valves in gas service:model development,measurements and instability mechanisms.J Loss Prev Process Ind 2014;31:70–81.

38.Rao YX,Yu L,Fu SW,Zhang F.Development of a butter fly check valve model under natural circulation conditions.Ann Nucl Energy 2015;76:166–71.

39.Afshari HH,Zanj A,Novinzadeh AB.Dynamic analysis of a nonlinear pressure regulator using bondgraph simulation technique.Simul Model Pract Theory 2010;18(2):240–52.

40.Tan JG,Jiang YP,Wang ZG.Instability characters and suppression method of a pressure regulator.J Braz Soc Mech Sci Eng 2013;35(1):1–10.