浅谈变式在课堂教学的应用
2018-06-27广东英德市英德中学石景学
广东英德市英德中学 石景学
目前高中的数学教学中,仍存在“满堂灌”和“题海战术”的教学模式。这种枯燥的教学方式不但让学生掌握情况差,也在慢慢的磨灭学生的自信与兴趣,最终导致学生成绩下降,甚至放弃对数学的研究和学习。面对这种情况,变式教学就显得尤为重要,通过变式为学生营造一种生动、活泼、宽松自由的氛围,开阔学生的视野,激发学生的情趣,有助于培养学生的探索精神和创新意识,并能使学生举一反三,事半功倍。老师也可通过变式教学提高课堂效率,减轻学生负担。本文结合自身的教学经历和学生实际情况,浅谈变式教学的应用。
一、变式教学在课前练习的应用
课前练习,一直是我校提倡的教学环节,该环节的时间一般控制在课间的前五分钟,设计一到两题的基础习题,帮助学生复习回顾上一节课的主要内容,而通过对习题的巧妙变式,可以流畅的把学生从复习上节课知识转移到对新知识的探究上,同时也为学生理解新知识做好铺垫,起到承上启下的作用。
二、变式在概念教学的应用
概念是数学学习的基础,学生对概念的理解、掌握程度直接关系到学生解题能力的强弱。现在的数学教学中,还有很多老师直接让学生对概念生搬硬套,忽视概念的形成、理解的教学过程,学生只知道概念的形,而不知概念的真正内涵,最终导致学生在解题时不会用或用错的现象比比皆是。为了让学生更好的理解概念,可充分利用变式,让学生从不同角度理解概念,形成完整的概念观,为学生正确的使用概念打下坚实基础。例如在《基本不等式》的概念教学中设计如下的例题和变式:
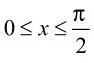
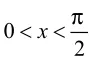
例1重点强调用基本不等式时,求和的最值积为定值,求积的最值和为定值。而变式2主要强调用基本不等式时,两数要为正数。变式3主要强调基本不等式取等号时两数要相等。通过上面的例题和变式,学生在短时间内经历了基本不等式成立的三个条件:一正,二定,三相等。既加深了学生对概念的理解和掌握,又为接下来正确使用基本不等式打下坚实的基础。
三、变式教学在巩固、拓展延伸的应用
随着新课改的深入和素质教育的大力实施,不但增添数学教学内容,也提高了数学的难度。教师除了要传授知识和解题方法,还要注重培养学生的探索精神、创新意识和解决问题的能力。这就意味着老师的教学任务越来越重,一题一得的教学方式显然已经满足不了现在的教学需求。如何在有限的时间提高课堂效率,减轻学生的学习负担成了很多老师头痛的问题。经实践证明,变式教学是一种行之有效的方法。利用一道简单的习题,提升学生的学习信心和学习热情,在通过巧妙地变式和拓展体会问题的来源,掌握分析问题、解决问题的一种基本方法,提高学生解决问题的能力,例如在《简单的线性规划》的学习中,可设计如下的例题和变式:




上述的例题与变式中,例2主要是为了帮助学生复习巩固线性规划中的截距型,也为接下来的变式做好准备。通过变式1,学生很快发现与例2的区别在于可行域含参,难点在于把可行域画出来,可引导学生给参数赋值,画出一个封闭的可行域,在结合截距型的解题方法,确定目标函数过哪点时取得最值,并把该点坐标求出,代入目标函数求出参数a。变式2中,把参数位置改为目标函数,引导学生发现封闭可行域的最优解必在可行域的端点处,可先求出三个端点,分别代入目标函数求出a,利用截距型的解题方法检验每个点求出的值是否满足题意,最终确定a的值。变式3中的最优解有无数个,学生首先想到出现这种情况只能是目标函数与可行域的直线平行,可假设目标函数分别与可行域中的直线平行求出值,并一一检验是否符合题意,最终确定值a。过程中老师以点拨、引导为主,充分体现学生的主体地位,既调动了学生积极性,又培养了学生探索求知的能力。并在相似背景下把高考考点三种含参试题都探究了一遍,不但提高了课堂效率,又减轻了学生负担。
四、变式教学在处理复杂问题时的应用
高中数学存在各式各样复杂的难题,学生面对这些复杂问题,往往是一头雾水,找不到方向。而老师对这类问题的讲解往往只是就题讲题,忽视学生的知识结构和认知习惯,导致学生过程中听不懂或听懂了但不能通解该类题,花了大量的时间和精力却得不到想要的结果。这种高投入,低产出的行为给学生造成过重的心理压力和心理负担,打击了学生的学习自信与热情,使学生产生厌学的情绪,长久以往不但学习成绩下降,甚至出现弃学现象。可通过变式,让学生经历从简单到复杂,循序渐进的探究过程,让学生不断加深对相关知识的理解,为解决最终复杂问题打下坚实的基础。
综上所述,变式教学可以用于课前练习,起承上启下的作用;用于概念教学,加深学生对概念的理解和正确使用概念;用于对知识的巩固、拓展延伸,提高课堂效率,减轻学生的学习负担;用于解决复杂问题,循序渐近的加深学生对问题的理解,最终解决复杂问题。总之,教学中适时的变式,有助于营造轻松、活泼的课堂氛围,激发学生的求知欲望,有助于提升学生的学习自信与热情。有助于培养学生的探索精神和创新意识。
