基于遗传算法的Low-E膜系中透明介质膜层均匀性在线分析

， ，，， ，(.，， 000； .， 000； .太阳能与建筑节能玻璃材料加工技术市， 000;.盛建材工程有限公司， 000; .， 0090)

1 前 言

随着建筑节能法规的强制实施及公众节能意识的增强，离线Low-E镀膜玻璃的用量在逐年增加，该类产品采用Ag薄膜实现低辐射效果，但由于Ag薄膜的金属属性需要利用透明介质膜层构成膜系，解决其附着力、耐环境、抗划伤等性能局限，同时需要通过各透明介质膜层与Ag膜层的光学匹配实现对产品光学性能及外观颜色的调控，以满足建筑设计要求。目前离线Low-E节能镀膜玻璃采用磁控溅射方式生产，能够生产最大宽度3300mm[1-2]，因此对膜层厚度均匀性提出了较高的要求。

为满足产品质量管控需求，离线Low-E镀膜生产线均配备有在线光学性能检测系统，用于监控产品玻面、膜面反射和透射光谱及颜色，若能利用在线光学系统测得的光谱数据分析介质膜层的厚度均匀性，将会在磁控溅射阴极安装调试及产品开发中具有重要的指导意义，因此本文将介绍依据膜面反射光谱、建立膜层柯西光学模型、基于遗传算法分析介质膜层厚度及折射率，以及结合各测量点颜色数据分析膜层厚度均匀性的方法。

2 光学模型

2.1 透明介质膜层特点

在离线Low-E膜系中常用到SiNx、SnOx、ZnOx、ZnSnOx、TiOx等透明介质膜层，这类膜层的厚度对实现产品的透光率、反射率和颜色等光学性能起到至关重要的作用[3]，在Low-E镀膜行业采用L*、a*、b*方式表示颜色空间，其中L*表示明度(Luminosity)，a*为横坐标，由正到负的变化表示颜色由红色变化至绿色；b*为纵坐标，由正到负的变化表示颜色由黄色变化至蓝色[4]。表1为开发的双银产品膜系结构，该膜系共10层，由于Low-E镀膜玻璃在使用时以玻面作为观察面，因此玻面反射(Rg)颜色是光学性能考察的重要指标[3]。图1为第9层ZnSnOx薄膜厚度变化对玻面反射颜色的影响，需要在溅射阴极调试时、产品膜系开发前首先解决单层介质膜层在镀膜宽度方向的均匀性问题，因此测试分析介质膜层厚度均匀性具有重要意义。

表1 双银产品膜系结构Table 1 Structure of Double-silver Low-E Film

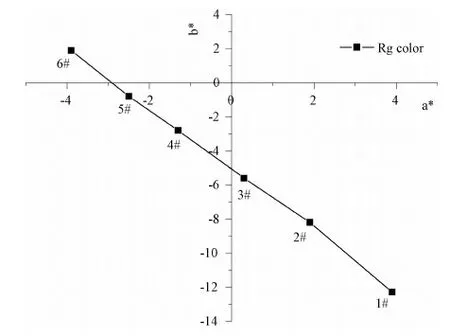
图1 玻面颜色随介质膜层(第9层ZnSnOx)厚度的变化Fig.1 Glass surface color with dielectric layer (No.9 ZnSnOx) thickness variation (1#11.6nm, 2#10.6nm, 3#9.6nm, 4#8.6nm, 5#7.6nm, 6#6.6nm)

2.2 膜层光学模型及与遗传算法的结合

膜层实际光谱可以通过在线光谱测量系统获得，本文采用的在线光谱测量装置安装于镀膜设备产品出口端，在镀膜玻璃宽度方向可以测得24个位置的380～780nm波长范围透射、玻面和膜面反射光谱，每测量点测试时间小于260毫秒；与其对应的理论光谱数据可以通过导纳矩阵法计算得到[5-7]，计算结果由膜层光学常数、厚度决定。对于透明介质膜层光学常数中消光系数k=0，折射率n随波长的色散关系可以用柯西(Cauchy)模型表示[8]，如式(1)。

(1)

式中：λ为波长，对于可见光范围取值380～780nm。

因此在已知实测光谱结果条件下，可以建立以膜层光学常数及厚度为未知数的特征矩阵方程[9]，求解膜层光学常数及厚度，但该方程涉及到三角函数、复数等复杂运算，很难获得解析解，但可以利用寻找最佳数值解的方法求解[10-12]。本文采用遗传算法寻找柯西模型参数及厚度的最佳解，根据遗传算法的编码定义[13-15]与本文讨论的问题存在以下对应关系：

基因：待求解的未知数，本文中为膜层折射率及厚度，由于以Cauchy模型表示膜层折射率色散关系，所以模型参数An、Bn、Cn及膜层厚度为基因；

个体：基因的一个组合，或称为染色体、对应于厚度、An、Bn、Cn的一个组合；

种群：多个体的组合，种群大小即为个体的数量；

评价函数：用于评价个体计算结果与测量结果的接近程度，或称为适应度函数，本文以膜面计算光谱反射率RfJ和膜面实测光谱反射率Rfc之间的均方差(MSE)表示[16](如式(2))，MSE越小越接近最佳解；

(2)

式中：n为光谱点个数，λi为光谱点。

终止条件：若满足终止条件，即得到最佳解，否则继续进行遗传过程，根据实际运算量设定满足MSE小于10-3或40次迭代即终止遗传过程。

通过以上的定义即可将问题转化为利用遗传算法寻找最佳个体(膜层厚度、An、Bn、Cn)的过程，该个体对应的膜面计算光谱反射率与实际测得的膜面光谱反射率之间的均方差值(MSE)最小。

3 数据分析流程及说明

3.1 总流程

本文以透明介质膜层SiNx薄膜为例说明厚度均匀性分析流程，如图2，膜层经在线测试得到各点的膜面反射光谱并计算得到膜面平均反射光谱及各点颜色，图3为SiNx薄膜24个测量点的膜面反射颜色的b*值。在分析过程中建立膜层Cauchy模型，依据膜面平均反射光谱，利用遗传算法获得膜层的折射率及平均厚度；再由分析得到的膜层折射率利用导纳矩阵法计算该膜层在一定厚度范围内各厚度对应的膜面反射光谱及颜色，形成颜色与厚度的关系，再利用线性插值得到各实测颜色对应的厚度值，形成膜层厚度的均匀性分布结果，其中计算的膜面反射颜色范围要大于测试得到的膜面反射颜色范围。

图2 通过遗传算法分析厚度均匀性流程Fig.2 Thickness uniformity analysis process based on genetic algorithm

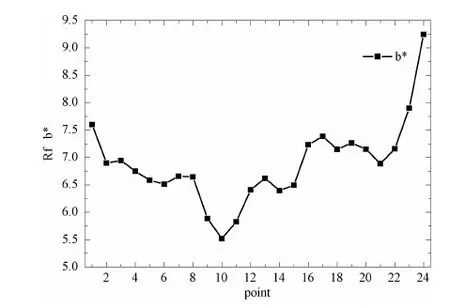
图3 SiNx膜层各点膜面反射颜色b*分布Fig.3 b* Value distribution of film surface reflection of SiNx film

3.2 折射率及厚度遗传算法分析流程

图2流程中的核心为根据膜面平均反射光谱由遗传算法分析膜层的折射率及平均厚度，其具体流程如图4所示，初始种群的生成和遗传过程由遗传算法标准过程完成[12-13]，导纳矩阵光谱计算过程有光学模型确定[5]，初始种群或新种群中的个体是导纳矩阵的输入参数，获得计算膜面反射光谱。由运算效率及精度分析本文中遗传过程的参数为：种群大小为35个个体、遗传迭代40次、精英数量为8个，交叉因素0.2[17]。通过图4流程获得的最佳解即为所测量的透明介质膜层的折射率柯西模型参数及膜层平均厚度。

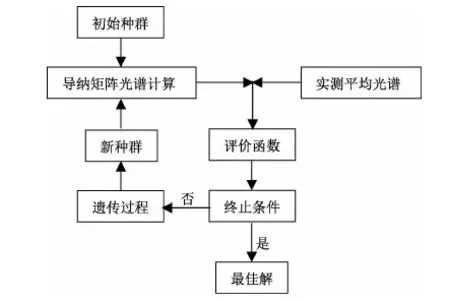
图4 遗传算法求解膜层柯西模型参数和厚度流程Fig.4 Process for solving Cauchy model parameters and thickness based on genetic algorithm

3.3 厚度均匀性分析流程

厚度均匀性分析流程如图5所示，以图3所测试的SiNx膜层为例，通过图2、4流程，得到膜层柯西模型参数为An=1.99609，Bn=0.00026757，Cn=0.00110583及平均厚度78.32nm，并由式(1)得到膜层折射率。一般生产中需要将膜层厚度均匀性控制在±2%，因此可以依据平均厚度设置厚度范围为75～85nm，利用已经分析获得的膜层折射率，计算75～85nm厚度范围内每变化1nm时，膜面的反射光谱及颜色，形成膜层厚度与颜色的b*之间的关系如图6所示。从图3、6可以看出，实际测量SiNx膜层膜面反射颜色b*分布范围为5.51～9.25，小于图6中颜色b*值范围，因此可以将实际测量颜色b*值按图6所示关系进行线性插值，得到各测量点厚度，如图7所示。

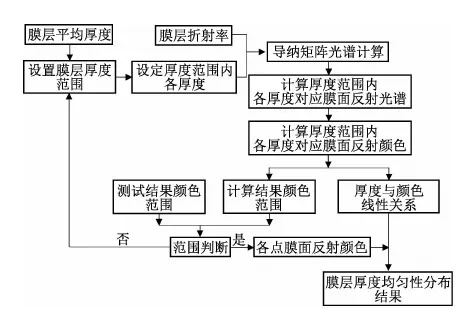
图5 厚度均匀性分析流程Fig.5 Process of thickness uniformity analysis

4 数据分析流程正确性讨论

4.1 利用膜面平均反射光谱的优势

本文中使用的在线光谱测量装置可以测得镀膜玻璃宽度方向24点的光谱数据，可以根据各点光谱利用图6所示流程分析各测量点折射率及厚度，但由遗传算法原理可知，对于每个测试点的分析过程将涉及到含有35个个体的种群、40次迭代运算，总运算光谱的数量达到33600个(24测量点×35个个体×40次迭代)，运算次数多、效率低，不适合于生产需求。由于在实际生产中同种膜层材料的折射率变化幅度极小，主要为沉积速率变化导致的厚度变化，因此采用膜面平均反射光谱获得膜层折射率能够反应膜层材料的本质特点；如本文 SiNx薄膜样品分析中，由获得的厚度与颜色变化关系，再根据实测颜色插值得到的厚度均匀分布数据，光谱计算个数仅为1411个(35个个体×40次迭代+11个设定厚度膜层光谱)，因此采用该方法可以极大地提高数据分析效率，计算耗时远小于24个测试点所需时间。

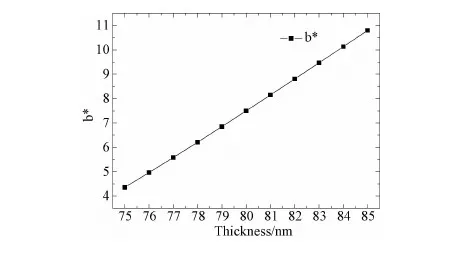
图6 膜层厚度与颜色b*值的变化关系Fig.6 Relationship between film thickness and b* value

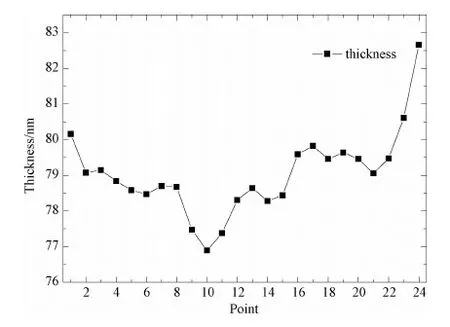
图7 膜层厚度均匀性分布Fig.7 Film thickness uniformity distribution

4.2 膜层厚度与反射颜色的变化关系

膜系表现出的光谱及颜色特征是膜层干涉的结果，图8为1～85nm范围内氮化硅SiNx薄膜与氧化钛TiOx薄膜颜色b*的变化，可以看出厚度与颜色b*的变化关系只能在较小的范围内近似为线性，而且膜层材料不同，折射率不同，变化的幅度也不同。如图9，TiOx薄膜折射率高于SiNx薄膜，相应的变化幅度也较大，因此不能直接利用测量的颜色数值判断实际厚度变化大小，而利用本文方法首先分析膜层的折射率及平均厚度，针对性地建立颜色与厚度的变化关系，提高了运算效率，同时保证了分析的正确性。

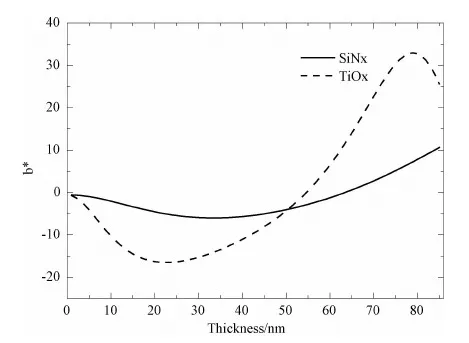
图8 SiNx、TiOx薄膜颜色的b*随厚度的变化Fig.8 b* value changes with thickness of SiNx and TiOx film

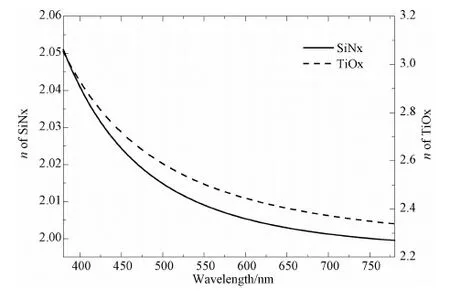
图9 SiNx、TiOx薄膜的折射率(n)Fig.9 Refractive index of SiNx and TiOx film

4.3 约束条件

遗传算法存在易提前收敛、稳定性差等问题[18]，因此在实践中需要根据材料特性及工艺条件对分析过程进行合理约束，如在合理工艺条件下SiNx、SnOx、ZnOx、ZnSnOx薄膜550nm波长处的折射率应在2.0～2.1，若分析结果超出该范围则说明有可能分析错误或工艺条件不合理，如对于反应溅射生成的SiNx薄膜，若设备存在真空漏气问题，将会使反应气体中存在氧气成分而使薄膜中含有氧化硅，导致薄膜折射率降低。膜面反射光谱的干涉级数可以体现出薄膜厚度的大致范围，另外介质膜层反应溅射沉积过程，在确定的功率条件下，反应气体量的变化与相应的溅射电压会体现出不同程度的“迟滞回线”现象[3]，因此通过光谱特征、溅射过程中电压与工艺气体量的变化关系可以分析厚度及其变化的合理范围[3,17]。

5 结 论

依据在线测试膜面反射光谱的结果建立光学模型，利用遗传算法能够快速、准确地分析介质膜层厚度的均匀性，适合于工厂实际生产条件应用。在分析过程中利用获得的膜层折射率及平均厚度，针对性地建立膜层材料在特定厚度范围内的颜色与厚度之间的关系，可以在保证分析结果正确性的同时提高数据分析效率。

[1] G. Bräuer. Large Area Glass Coating[J]. Surface and Coatings Technology, 1999, 112:358～365.

[2] C. Schaefer, G. Bräuer, J. Szczyrbowski. Low Emissivity Coatings on Architectural Glass[J]. Surface and Coatings Technology, 1997, 93:37～45.

[3] 汉斯·琼彻·格雷瑟. 大面积玻璃镀膜[M]. 第1版,上海:上海交通大学出版社, 2006：83～136.

[4] Günter. Wyszecki, W.S. Stiles. Color Science, Concepts and Methods, Quantitative Data and Formulae[M]. Second, New York, John Wiley & Sons, 1982:10～120.

[5] Y. Laaziz, A. Bennouna, M.Y. Elazhari. A Method for Monitoring the Thickness of Semiconductor and Dielectric Thin Films: Application to the Determination of large-area Thickness Profiles[J]. Thin Solid Films, 1997, 303:255～263.

[6] JIANG Daoping, JIA Hongzhi, LU Huancai. Calculation for the Optical Parameters of the Sn-doped SiO2Thin Films by Fitting the Entire Transmitted Spectrum[J]. Optik-Int J Light Electron Opt, 2013, 124:102～106.

[7] Sanjaykumar J. Patel, Vipul Kheraj. Optimization of the Genetic Operators and Algorithm Parameters for the Design of a Multilayer Anti-reflection Coating using the Genetic Algorithm[J]. Optics & Laser Technology, 2015, 70:94～99.

[8] 唐晋发,顾培夫,刘旭,李海峰. 现代光学薄膜技术[M]. 第1版. 杭州:浙江大学出版社, 2006：403～470.

[9] 李镇涛,王振家,赵大庆. ZAO/metal/ZAO多层膜光学性能优化设计[J]. 材料科学与工程学报, 2004, 22(4):495～497.

[10] 叶美盈. 基于整体退火遗传算法的膜系设计方法[J]. 光电工程, 2000, 27(3):12～15.

[11] 吴素勇,龙兴武.基于遗传算法的减反射膜的优化设计[J]. 应用光学, 2008, 29(4):542～547.

[12] 范志刚,张爱红,李洪兵. 基于遗传算法的光学膜系初始结构优化设计[J]. 光学技术, 2002, 28(6):513～517.

[13] 邢文训,谢金星.现代优化计算方法[M].第二版. 北京:清华大学出版社, 2007：113～119.

[14] Randy L. Haupt,Sue Ellen Haupt. Practical Genetic Algorithms [M]. Second, Hoboken, John Wiley & Sons, 2004:22～47.

[15] 张纯禹. 现代优化计算方法在材料最优化设计中的应用[J]. 材料科学与工程学报, 2003, 21(1):44～47.

[16] 赵利,薛亦渝,王学华,张幼陵. 膜系自动设计中的几种新型评价函数[J]. 武汉理工大学学报:信息与管理工程版, 2002, 24(5): 125～127.

[17] 余刚,汪洪. 基于遗传算法透明介质膜层折射率及厚度在线分析[J]. 硅酸盐学报, 2016, 44(1):148～154.

[18] 李险峰,董绍华.改善收敛早熟的混合遗传算法[J]. 计算机系统应用, 2011, 20(10):224～227.