含间隙齿轮碰振系统的全局动力学分析*
2018-06-25张思进王紧业文桂林
张思进 王紧业 文桂林
(湖南大学机械与运载工程学院,长沙 410082)
引言
非光滑动力学系统以其表现出的与光滑系统截然不同的动力学特性而备受学者关注.其中,齿轮系统就是典型的分段线弹性碰振系统,具有非常复杂的非光滑动力学特性.众所周知,齿轮系统是各类机械设备的主要传动装置,齿轮系统的动力学特性直接影响着机械设备的工作稳定性能和可靠性,因此研究齿轮系统碰振动力学意义重大.
王建平[1]等人以含有动态刚度、传递误差和齿侧间隙的直齿轮系统为研究对象,齿侧间隙拟合成3次多项式的形式,分析齿轮系统在参数激励、内部激励和外部激励共同作用下的组合共振特性.Natsiava[2]等人研究了具有时变系数及弱非线性特性的齿轮副系统,运用经典的摄动分析方法,消去久期项确定了周期解的存在,并验证了周期解的稳定性.祁常君等人[3]研究了齿侧间隙和随机齿侧间隙两种情况对齿轮系统的动力学影响.张晨旭[4]等将间隙分段函数拟合为光滑函数,对比了拟合后齿轮传动系统与原非光滑系统的动力学行为.有关多自由度齿轮系统的更多文献见[5-9],这些文献更多的是用数值模拟或拟合多项式方法来处理分段函数对齿轮系统的影响,而从非光滑动力学理论的高度来研究齿轮系统动力学特性的工作相对较少.
本文将齿轮系统中的间隙函数直接视为分段线性函数,不做多次项拟合处理,因而能更好反应齿轮系统的实际啮合状况.通过拓展Melnikov方法使其适用于分段连续函数,并借助该方法分析了系统全局异宿轨道分岔的条件.然后,求得每个分段方程的解析通解并以切换面作为Poincaré截面,进一步建立了分段光滑动力学系统的Poincaré映射.通过对组合映射的分析,确定了系统周期碰振运动的稳定性.最后,运用数值方法模拟了阻尼,弹簧刚度及外部激励对系统周期解及复杂混沌运动的影响.
1 系统运动微分方程
假定齿轮系统的传动轴为刚性且考虑支撑轴的扭振,建立如图1所示一个等效的主动轮单自由度简化模型,主动轮的转动惯量等特性等效为质块M,与从动轮啮合时刚度系数和阻尼系数均发生改变(从动轮未给出),这里仅分析主动轮的运动状态.质量为M的主动轮由等效刚度系数为K1的线性弹簧和等效阻尼系数为C的阻尼器连接于支撑板,同时受简谐激力PcosΩτ的作用在水平方向移动.以轮齿之间的间隙中点建立坐标系,当质量块的位移等于B时,将会与刚度为K2的弹簧(右边)接触即齿轮开始啮合,一段时间后啮合开始分离,然后质块M位移等于-B时再与刚度为K2的弹簧(左边)接触,如此反复啮合运动.

图1 含间隙弹性约束齿轮系统啮合的简化模型Fig.1 Simplified model of restrain gear system with clearance
图示主动轮的运动微分方程可表示如下:
(1)
式中:
(2)
对方程(1)和(2)进行无量纲化处理,形式如下:
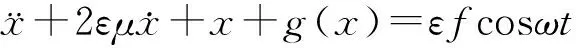
(3)

(4)

因此,可得:
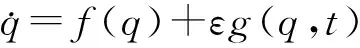
(5)


图2 分段函数表达式Fig.2 Expression of the piecewise function
图2表示齿轮副啮合接触前后引起的轮齿间弹性力的变化过程.可见,齿轮系统的啮合过程是典型的分段光滑动力学行为,会呈现出复杂的倍周期分岔和混沌等非线性动力学现象.
2 异宿轨道Melnikov全局分析方法
这里研究的齿轮啮合系统中含有分段函数,导致Melnikov方法不能很好的应用于非光滑动力学系统当中.因此,必须对Melnikov函数进行相应的拓展以适应非光滑系统.首先将系统(3)的未扰系统(令ε=0)重新整理为如下形式:
(6)
这里,分段Hamilton函数可以表达为如下形式:
当x≤-b时,分段系统的Hamilton函数为:
(7)
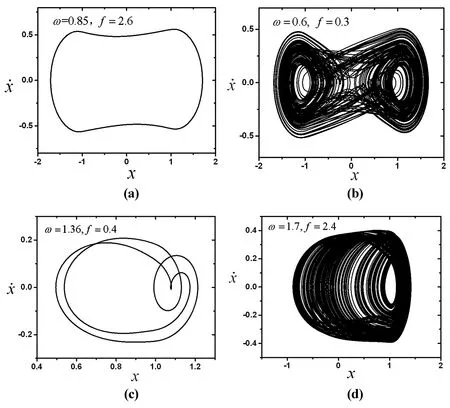
当|x| (8) 当x≥b时,分段系统的Hamilton函数为: (9) 通过计算可知,系统(6)存在着三个平衡点,其中(0,0)为中心型,(±βb/(1+β),0)为鞍点型.因此,系统(6)存在着如图 3所示的分段非光滑异宿轨道. 图3 未扰异宿轨道示意图Fig.3 Heteroclinic orbit of the unperturbed system 由图3知系统的非光滑异宿轨道具有对称的特性,这里只考虑y>0的情况.因此,分段形式的异宿轨道表达式如下: 当x≤-b时, (10) 当|x| (11) 当x≥b时, (12) 上述3段非光滑分段异宿轨道把鞍点(±βb/(1+β),0)的稳定流形和不稳定流形链接在一起如图 4,ε表示小的数量级.系统中的异宿轨道是接下来要研究的主要问题. 图4 扰动系统的稳定流形与不稳定流形Fig.4 Stable and unstable mainfold of perturbed system (13) (14) 假设: (15) 其导数在光滑条件下成立(即离开切换面时), (16) 由此我们可以定义以下能量函数: (17) 因此,可得: O(ε2) (18) 其中, 由参考文献[10]可得分段光滑动力学系统的Melnikov函数为: (19) 依据动力学系统的Melnikov理论[11-12],系统产生混沌的参数条件为: (20) 方程(20)定义的临界线将参数区域(εf,ω)分为周期区域和非周期区域如图5.其中,位于水平线(f=0)下方的取值表示外激励力的方向与规定的正方向相反.当εf的取值位于分界线的非周期区域时,系统可能会出现混沌运动的状态;εf的取值位于分界线的周期区域时,系统的运动状态呈现出有规律的周期特性.为了验证上述结论,这里选取分别位于周期区域的A点、C点和位于非周期区域的B和D点进行数值仿真,并逐一列出了四个点的相图,如图6所示. 图5 全局异宿分岔的参数域Fig.5 Parametric regions of global heteroclinic bifurcation 图6 临界线取点对应的系统相图Fig.6 Phase portrait of the points above/under the critical line 改变外激励频率和外激励力的取值,观察齿轮系统的非线性动力学特性.从图6((a)-(d))四幅图中可以得知:A点取值ω=0.85,f=2.6时,系统呈现出单倍周期运动状态;改变频率和激励力的取值为ω=0.6,f=0.3,(b)相图表明此时系统处于复杂的混沌状态;然而,当位于C点处的取值为ω=1.36,f=0.4时,相图(c)表明系统处于四倍周期运动状态;频率进一步增加时,D点处的相图最终通向了混沌运动如图(d).可见,参数ω,f发生变化时,齿轮系统表现出周期运动和混沌运动交替出现的规律. 方程(3)在各分段条件下的解析解[13-14]如下: x(t)= e-μ(t-t0)[c1cosη(t-t0)+c2sinη(t-t0)]+ Acosω(t+t0)+Bsinω(t+t0) (21) e-μ(t-t0)(-μc1+ηc2)cosη(t-t0)- e-μ(t-t0)(ηc1+μc2)sinη(t-t0) (22) c1=b-Acost0-Bsint0, c2=(y0+Aωsint0-Bωcost0+μc1)/η. Ccos(ωt+t1)+Dsin(ωt+t1) (23) (24) 其中, c3=x1-Ccost1-Dsint1-βb/(1+β) x≤-b时与上述情况类似,这里不再给出详细的通解表达式. 将分段解的表达式结合起来,利用区域与区域间的边界条件,即可建立系统运动的Poincaré映射关系[15-16],从而得到系统的周期解进而分析其运动稳定性.首先,我们构造了质量块M与右边弹簧的映射关系,P1表示物块M与右边弹簧发生碰撞时的接触状态,P2表示物块M与右边弹簧碰撞完成后的脱离状态. 图7 切换面及基本映射关系图Fig.7 Relationship between witching planes and basic mappings 映射关系P1可以由式(21)和(22)构造: e-μ(t-t0)[c1cosη(t-t0)+c2sinη(t-t0)]+ Acosω(t+t0)+Bsinω(t+t0)-b=0 (25) e-μ(t-t0)(-μc1+ηc2)cosη(t-t0)- e-μ(t-t0)(ηc1+μc2)sinη(t-t0) (26) 映射关系P2可以由式(23)和(24)构造: Ccos(ωt+t1)+Dsin(ωt+t1)-b=0 (27) (28) 同理可以得到质量块M与左边弹簧的映射关系P3和P4以及映射表达式,这里不再详细列出. 因此Poincaré映射可以表示为: DP=DP1·DP2·DP3·DP4 (29) 为了讨论此新系统周期碰振运动的稳定性,我们还需要计算Poincaré映射P在不动点处的Jacobi矩阵.依据隐函数求导法则,其线性化矩阵可以由下面的表达式得到(因表达式过于复杂,本文略去详细结果): (30) 根据(30)式在不动点处的特征根,我们可以得到系统周期运动的稳定性.数值仿真得到质量块M与左、右边弹簧接触和外激励共同作用下的整体运动特性见下图. 图8 双边碰振时系统的周期1相图Fig.8 Period-1 phase portrait of bilateral impact 图9 双边碰振时系统的周期4相图Fig.9 Period-4 phase portrait of bilateral impact 图10 全局混沌运动相图Fig.10 Global phase diagram of chaotic motion 取值β=0.8及间隙b=1不变,阻尼μ=0.32时可以得到质量块M与左右两边的弹簧发生碰撞,齿轮系统的运动状态处于稳定的单周期运动如图8所示;减小阻尼值,当阻尼位于μ=0.24附近时相图变为图9所示的闭合曲线,系统由稳定的单周期运动变为了稳定的周期四运动;阻尼值继续减小到0.13,此时平面相图变成了比较杂乱的曲线,齿轮系统已经由稳态状态进入了混沌响应特性.由上述分析可知,适当的控制阻尼系数μ的值,可以避免齿轮系统出现多周期运动和混沌运动的情形. 建立齿轮副主动轮的单自由度非线性动力学模型,并将齿轮系统中的间隙函数视为分段线性函数,在此基础上研究含间隙齿轮系统碰振的全局特性及周期运动的稳定性,更好地反应齿轮的实际啮合状况. (1)通过拓展Melnikov方法使其适用于分段连续函数,并借助该方法分析了系统异宿轨道的全局运动,得到了全局异宿轨道分岔的条件. (2)建立分段非光滑动力学系统的Poincaré映射,分析了系统的简单周期碰振运动的稳定性. (3)运用数值方法计算分岔图中不同区域参数对应的相图.得到系统相应的运动轨线,验证Melnikov方法分析分段非光滑系统的有效性. 1王建平,王玉新. 运用多尺度法对齿轮系统组合共振特性的分析. 西安理工大学学报, 2005,21(1):5~10 (Wang J P, Wang Y X. Combination resonance of spur gear system analyzed using multi-scale approach.JournalofXi′anUniversityofTechnology, 2005,21(1):5~10 (in Chinese)) 2Natsiavas S, Theodossiades S, Goudas I. Dynamic analysis of piecewise linear oscillators with time periodic coefficients.InternationalJournalofNon-LinearMechanics, 2000,35(1):53~68 3祁常君,苟向锋,陈代林. 随机齿侧间隙的齿轮系统非线性动力学分析. 兰州交通大学学报, 2014,33(3):54~58 (Qi C J, Gou X F, Chen D L. Nonlinear dynamic analysis of the gear system with stochastic backlash.JournalofLanzhouJiaotongUniversity, 2014,33(3):54~58 (in Chinese)) 4张晨旭,杨晓东,张伟. 含间隙齿轮传动系统的非线性动力学特性的研究. 动力学与控制学报, 2016,14(2):115~121 (Zhang C X, Yang X D, Zhang W. Study on non-linear dynamics of gear transmission system with clearance.JournalofDynamicsandControl, 2016,14(2):115~121 (in Chinese)) 5Rocca E, Russo R. Theoretical and experimental investigation into the influence of the periodic backlash fluctuations on the gear rattle.JournalofSoundandVibration, 2011,330(20):4738~4752 6Li Z, Peng Z. Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: a case study on coal cutters.NonlinearDynamics, 2015,84(1):271~286 7Guerine A, El Hami A, Walha L, et al. A polynomial chaos method for the analysis of the dynamic behavior of uncertain gear friction system.EuropeanJournalofMechanics-A/Solids, 2016,59:76~84 8Liu H, Zhang C, Xiang C L, et al. Tooth profile modification based on lateral- torsional-rocking coupled nonlinear dynamic model of gear system.MechanismandMachineTheory, 2016,105:606~619 9Wei S, Han Q, Peng Z, et al. Dynamic analysis of parametrically excited system under uncertainties and multi-frequency excitations.MechanicalSystemsandSignalProcessing, 2016,72:762~784 10 Li S, Zhang W, Hao Y. Melnikov-Type Method for a Class of Discontinuous Planar Systems and Applications.InternationalJournalofBifurcationandChaos, 2014,24(2):1~10 11 张思进,文桂林,王紧业等. 碰振准哈密顿系统局部亚谐轨道的Melnikov方法. 振动工程学报, 2016,29(2):214~219 (Zhang S J, Wen G L, Wang J Y, et al. The Melnikov′s method for local-subharmonic orbits of a vibro-impact quasi-Hamiltonian system.JournalofVibrationEngineering, 2016,29(2):214~219 (in Chinese)) 12 Zhang S J, Ji D S, Wen G L, et al. Analysis of Global Subharmonic Orbits of a Vibro-Impact Quasi-Hamiltonian System with the Melnikov′s Method.DynamicsofContinuous,DiscreteandImpulsiveSystems,SeriesB:Applications&Algorithms, 2015,22(1):69~84 13 Luo A C J. The mapping dynamics of periodic motions for a three-piecewise linear system under a periodic excitation.JournalofSoundandVibration, 2005,283(5):723~748 14 赵文礼,王林泽. 机械振动系统随机疲劳和间隙非线性. 北京:科学出版社, 2006 (Zhao W L, Wang L Z. Random fatigue of mechanical vibration system and backlash nonliearity. Bejing: Science Press, 2006 (in Chinese)) 15 Zhang S J, Wen G L, Peng F, et al. Analysis of limit cycle oscillations of a typical airfoil section with freeplay.ActaMechanicaSinica, 2013,29(4):583~592 16 尹磊磊,张思进,文桂林等. 间隙约束二元翼段系统分岔与多解共存现象分析. 航空动力学报, 2014,29(6):1410~1416 (Yin L L, Zhang S J, Wen G L, et al. Analysis on the system bifurcation and coexistence of multiple solutions for typical airfoil section with freeplay.JournalofAerospacePower, 2014,29(6):1410~1416 (in Chinese))

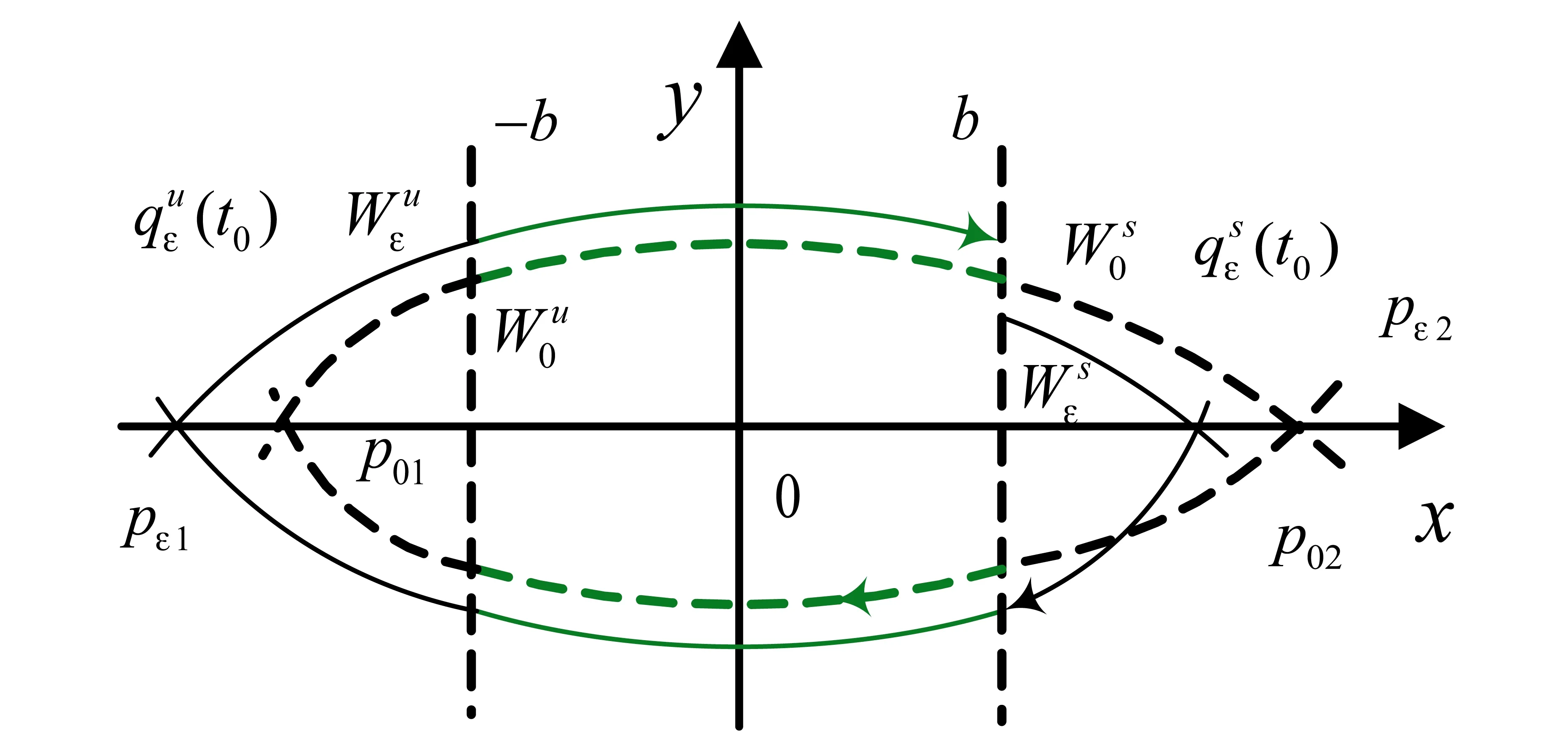
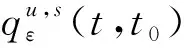

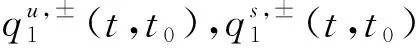



3 周期运动稳定性分析
3.1 分段方程的解析通解


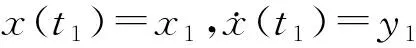
3.2 Poincaré映射及稳定性分析




4 结论
