基于频率拓展的表面多次波压制方法

李星缘， 王维红， 王海娇， 张文武

( 东北石油大学 地球科学学院，黑龙江 大庆 163318 )

0 引言

简单地区油气勘探基本完毕，随着油气需求量的增大，复杂介质的地震资料处理方法被广泛关注。尤其是存在大量多次波的地震剖面，会产生构造假象、解释困难等问题，多次波的压制一直是地震数据处理，尤其是表面多次波丰富的海洋勘探亟待解决的问题之一。

常规的多次波压制方法主要包括滤波法和预测相减法。滤波法利用多次波和一次波之间的运动学差异压制多次波，预测相减法是以波动方程为基础，利用一次波和多次波之间的动力学差异压制多次波[1-3]。在简单的油气勘探区域，地质条件良好，一次波和多次波有较大时差，滤波方法可有效压制多次波，且具有计算成本低的特点；与滤波法相比，预测相减法的优点是无需地下介质的先验信息，可更好地适应构造复杂的地区[4]。Backus提出的预测反褶积方法是最早被应用的滤波法，对地质条件要求较高，不能广泛应用于石油勘探[5]。基于反馈迭代模型，Berkhout和Verschuur将地下地震波传播过程用数据矩阵方式表示，并提出预测自由表面多次波的算法，在模型和实际数据中得到相对较好的结果[6]。Van Dedem利用稀疏参数反演方法，将多次波预测拓展到三维地震资料处理中。石颖等引入GPU技术压制表面多次波，极大地提高反馈迭代法的计算效率[7]。

无论是反馈迭代法预测多次波，还是波场延拓法预测多次波，得到的多次波存在振幅、频率、相位和旅行时的差异，从原始数据中直接减掉预测的多次波，往往得不到好的多次波压制效果。主要原因是多次波预测过程产生子波效应，使预测的多次波高频变弱，频带能量差异变大，进而影响有效波的频带。基于频率拓展的多次波压制方法，根据最小二乘原则，笔者改善预测多次波的频率特性，对它进行升频处理，使预测的多次波与实际的多次波吻合，压制效果良好。

1 基本原理

1.1 多次波预测实现

Berkhout和Verschuur用数据矩阵的概念将波场延拓表示成空间褶积的形式，在WRW模型的基础上，提出SRME方法压制多次波[8]。原理为

P(z0,z0)=D(z0)ΔX(z0,z0)[S(z0)+R(z0,z0)P-(z0,z0)],

(1)

式中：P(z0,z0)为含有有效波和多次波的地震波场；D(z0)为检波器特性矩阵；ΔX(z0,z0)为不含表面多次波的地下脉冲响应矩阵；S(z0)为震源波场特性矩阵；R(z0,z0)为反射系数矩阵；P-(z0,z0)为自由界面处的上行波场，上行波场不是直接测量得到的地震数据。在自由表面反射层处，上行波发生反射转化成下行波，下行波场不仅包含震源波场S(z0)的信息，而且也包含上行波场的信息。

一次波是指没有经过自由界面反射的波，即

P0(z0,z0)=D(z0)ΔX(z0,z0)S(z0),

(2)

多次波场可表示为

M(z0,z0)=D(z0)ΔX(z0,z0)R(z0)P-(z0,z0),

(3)

可得

M(z0,z0)=P(z0,z0)A(z0)P0(z0,z0),

(4)

式中：A(z0)=S(z0)R(z0)D(z0)。由于在多次波预测之前，无法得到有效波，将过程写成一种迭代的形式，即

(5)

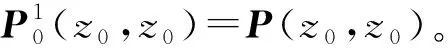
1.2 多次波压制方法

多次波预测过程中，至少多褶积一个地震子波，产生子波效应，导致预测多次波与实际数据存在能量不匹配[10]。基于频率拓展的表面多次波压制方法，能消除预测过程中产生的子波效应，解决预测多次波与原始数据在频率上的差异。

自适应匹配滤波方程为

(6)

式中：P0(t)为有效波地震数据道；P(t)为原始数据道；N为多次波模型道的道数；fi(t)为自适应匹配滤波器；mi(t)为预测的多次波，即

(7)

基于频率拓展的表面多次波压制方法利用最小能量准则[11-13]，目标函数为

(8)

对f求导，得到线性方程组形式，即

(9)

式(9)方程可简化为

Ax=b,

其中：

(10)

最后，利用奇异值分解方法得到自适应滤波器fi(t)。在自适应相减过程中进行迭代，可增加滤波器的长度，提高自适应匹配相减的精度，进而改善多次波压制效果。

以单道匹配滤波为例，原始自适应匹配方程可表示为

P0(t)=P(t)-f(t)*m(t)。

(11)

可构造迭代相减方法为

(12)

式中：j为减法迭代次数；F(j)(t)为与f(j)(t)相关的匹配滤波器。

以2次迭代为例，有效波的迭代形式可表示为

(13)

式中:F(2)(t)为实际的匹配滤波器，F(2)(t)=f(2)(t)*f(1)(t)。令每次迭代中滤波器的长度为l，最终的滤波器长度为2l-1。长滤波器对多次波的压制效果更为明显，但损害有效波的能量，短滤波器压制多次波存在残留，需要选择一个可以平衡压制多次波能量和保护有效波能量的滤波器。通过迭代方法实现多次波压制，选择稍短的滤波器，既可以保护有效波能量，又能保留长滤波器的优势，最大限度地压制多次波。在算法实现的过程中，应用迭代可得到更好的多次波压制结果，但迭代次数的增加使计算效率下降，利用基于频率拓展的最小二乘匹配方法压制多次波，通常进行2次迭代就能得到较为精准的有效波数据，计算成本较低，具有很强的实用性。

2 应用实例

2.1 水平层状模型测试

水平层状模型共800道，道间距为15 m，时间采样间隔为4 ms，时间方向为1 500个采样点。通过SRME方法预测多次波并对结果进行频谱分析(见图1)。由图1可知，预测的多次波频带明显变窄，原因是预测过程中多余的子波效应影响预测多次波的精度[14-16]。采用基于频率拓展的最小二乘自适应减法后，压制多次波后的有效波地震数据频带比预测的多次波频带拓宽15 Hz，与原始地震数据频带基本一致。

为验证基于频率拓展的表面多次波压制方法的适用性，采用含有多次波的水平层状介质的单炮记录进行测试分析(见图2(a))。对水平层状模型进行多次波预测及压制，预测得到多次波数据单炮记录见图2(b)。对比图2(a)与图2(b)可知，有效波的能量远大于多次波的能量，即强有效波周围被弱多次波所包围。压制多次波后有效波数据的单炮记录见图2(c)。由图2(c)可知，多次波得到有效压制。因此，利用基于频率拓展的表面多次波压制方法，能够压制原始数据中的多次波数据，并且不损害有效波数据。

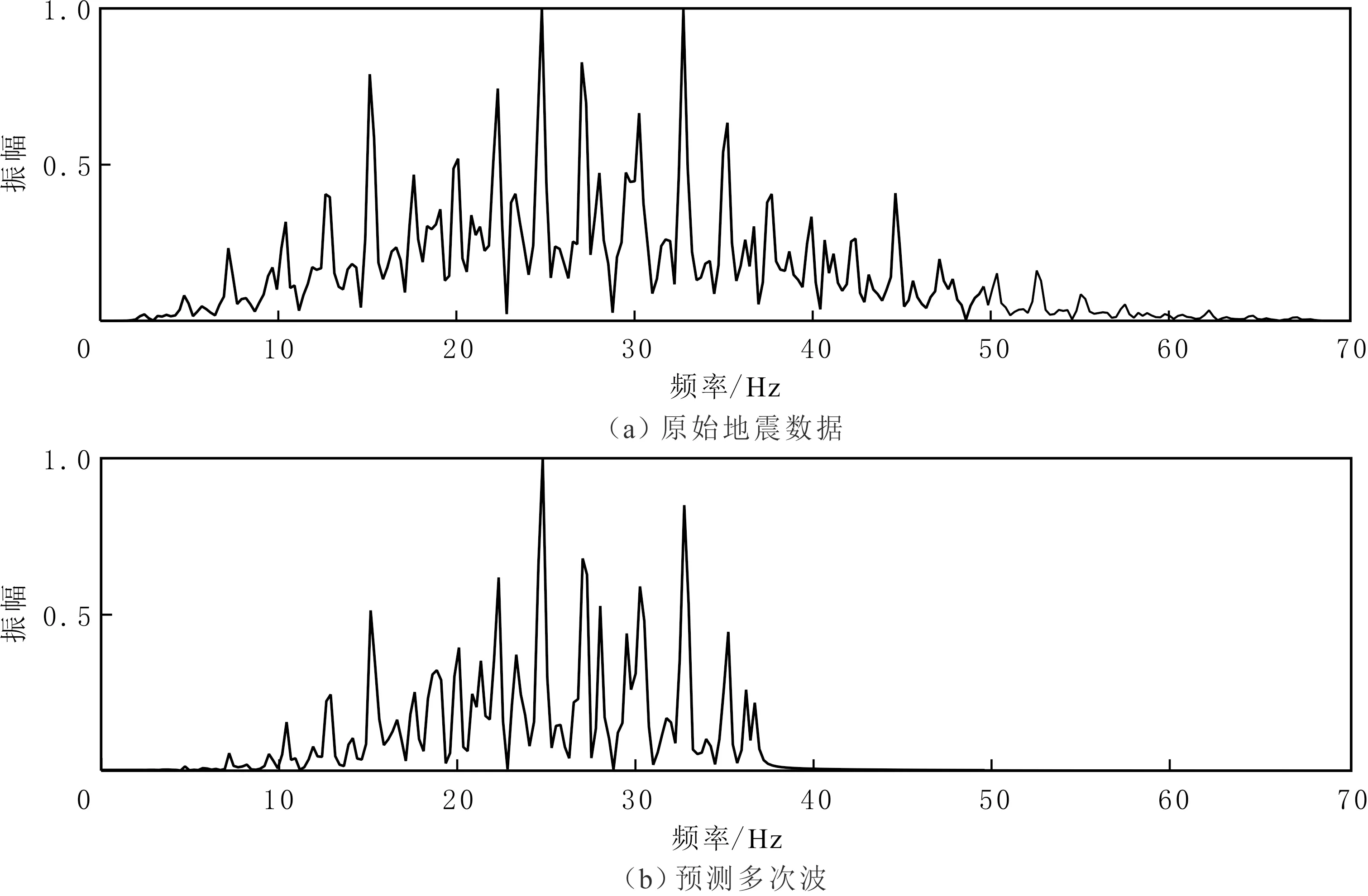
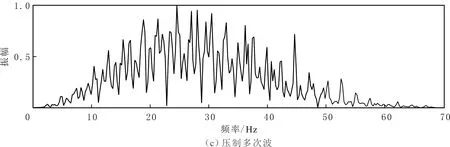
图1 地震数据频谱分析Fig.1 Seismic data spectrum analysis diagram

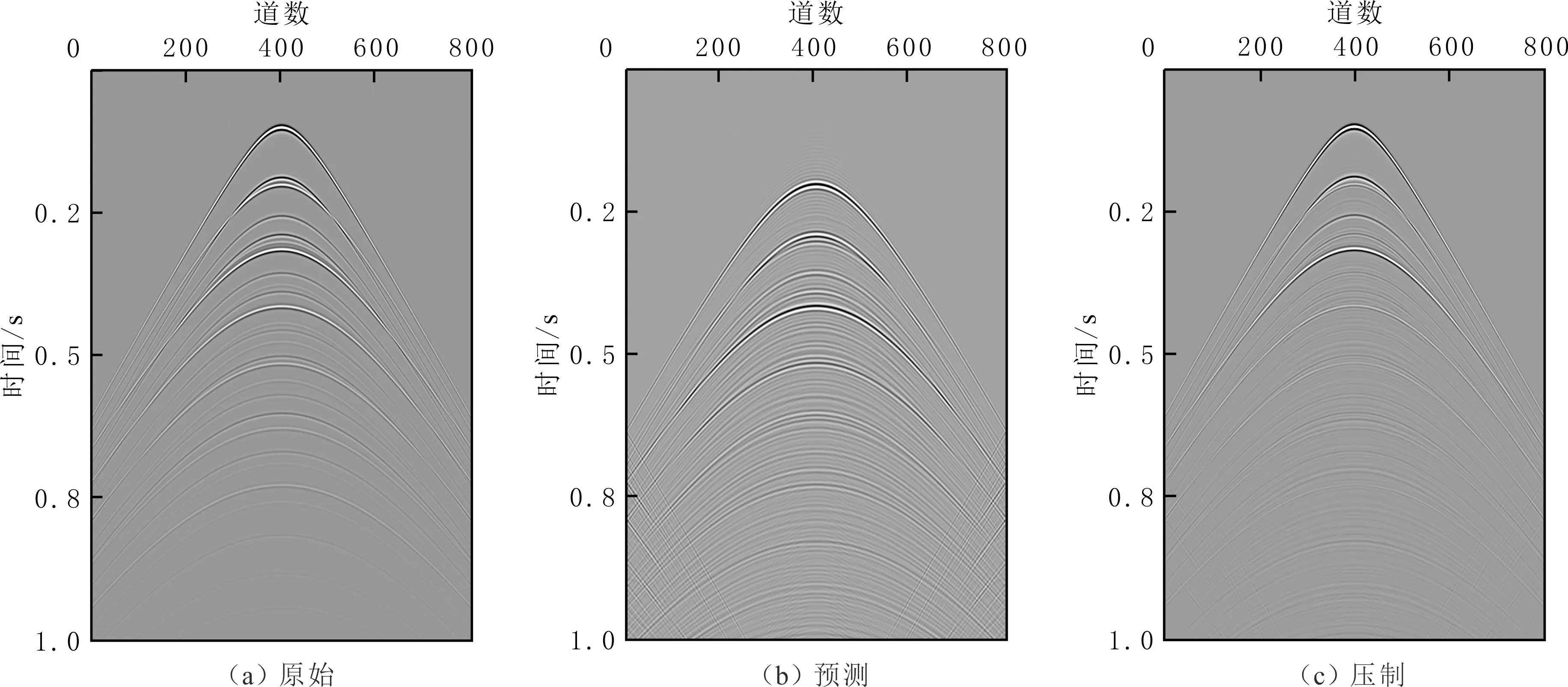
图2 水平层状模型表面多次波预测及压制单炮记录Fig.2 Surface-related multiple prediction and suppression on synthetic horizontal layered model

2.2 SMAART模型测试

为验证基于频率拓展的表面多次波压制方法的有效性，对构造相对复杂，含有丰富表面多次波的SMAART模型进行测试并抽取单炮记录[17-19](见图3)。由图3可知，多次波得到有效压制。为了更加直观地展示对多次波的压制效果，抽取该炮的某一道进行对比分析(见图4)。由图4可知，该算法压制多次波的效果明显。

对该算法的抗噪性进行测试，在原始数据中添加随机噪声，得到信噪比为12的数据。对该数据进行测试分析，得到添加随机噪声后的SMAART模型表面多次波预测及压制单炮记录(见图5)。由图5可知，随机噪声影响很小，该算法稳定性较强。

另外，以SMAART模型为例，对该算法的计算效率进行测试。在预测部分，采用GPU/CPU协同并行技术对算法进行加速，用时26 s。自适应相减部分为单道的相减，完成一道的自适应相减的时间为0.3 s。该算法的计算效率满足工业要求。

2.3 效果对比

为了分析基于频率拓展的表面多次波压制方法的优越性，同传统Radon变换滤波法做对比，对SMAART模型数据进行测试分析(见图6)。由图6可知，利用传统Radon变换滤波法压制多次波后，复杂构造模拟数据中的有效波同相轴的连续性没有得到很好的保持，基于频率拓展的表面多次波压制方法得到的结果较好，但是计算量同传统Radon变换滤波法相比稍大。

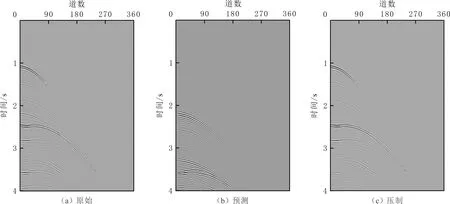
图3 SMAART模型表面多次波预测及压制单炮记录Fig.3 Surface-related multiple prediction and suppression on synthetic SMAART model

图4 单道对比Fig.4 Single-lane comparison chart

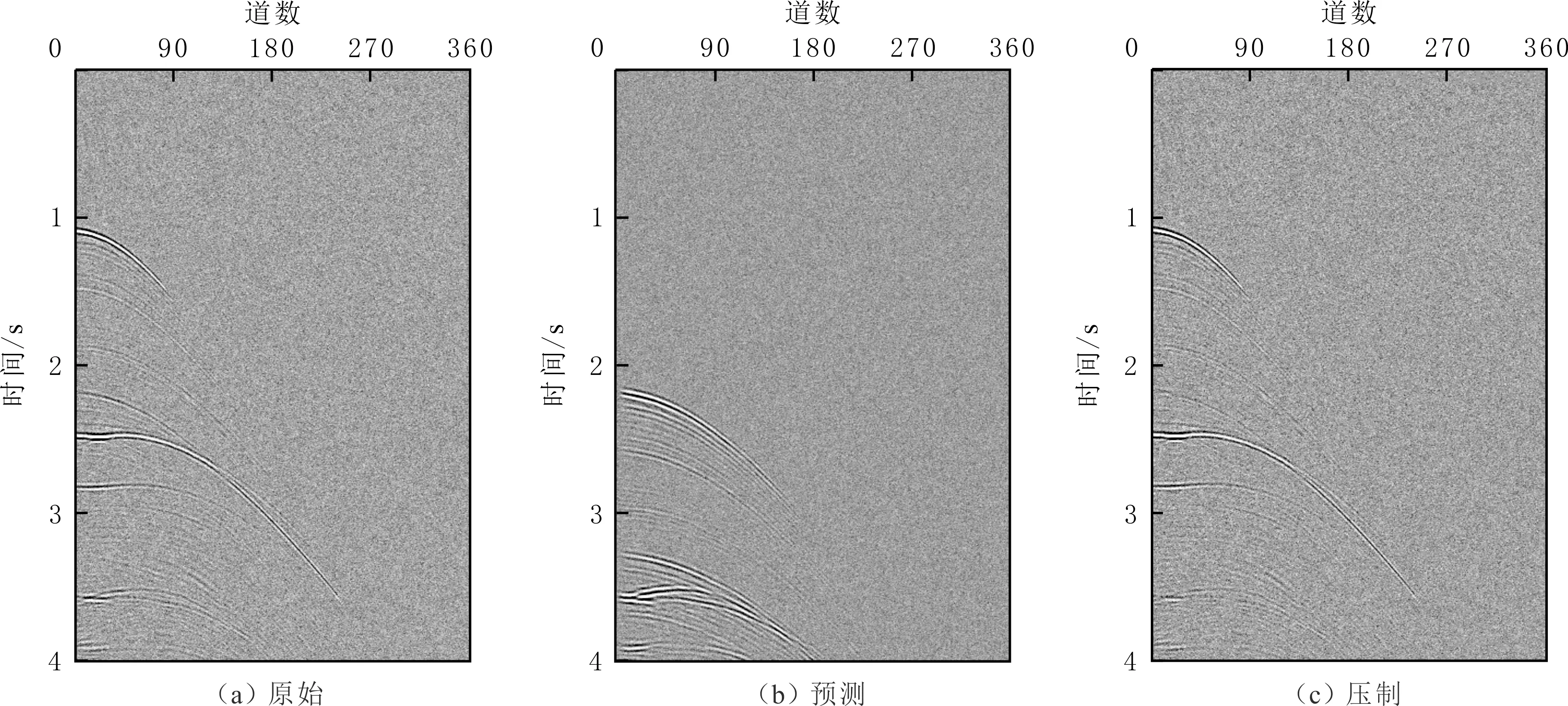
图5 添加噪声后的SMAART模型表面多次波预测及压制单炮记录Fig.5 Surface-related multiple prediction and suppression on synthetic SMAART model with noise

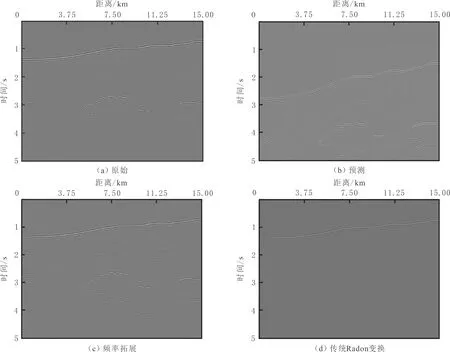
图6 SMAART模型表面多次波压制效果对比Fig.6 Comparative analysis of surface multiple repression on SMAART model

3 结论

(1) 对水平层状模型、SMAART模型的试算，基于频率拓展的表面多次波压制方法能消除预测过程中的子波效应，并且对地质结构较复杂的模型也能有效压制多次波。

(2) 基于频率拓展的表面多次波压制方法计算量小，通常进行2次迭代就能得到良好的多次波压制结果。

(3) 通过与传统Radon变换滤波法压制多次波对比，基于频率拓展的表面多次波压制方法对多次波压制效果更为彻底，并且没有损害有效波能量。

参考文献(References):

[1] Berhkout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, part Ⅰ: Theoretical considerations [J]. Geophysics, 1997,62(5):1586-1595.

[2] Wang Y H. Multiple prediction throught inversion: A fully data-driven concept for surface-related multiple attenuation [J]. Geophysics, 2004,69(2):547-553.

[3] Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, part Ⅱ: Practical aspects and examples [J]. Geophysics, 1997,62(5):1596-1611.

[4] 何江.基于L1范数的多次波自适应减方法研究及应用分析[D].北京:中国地质大学(北京),2012.

He Jiang. Research and application analysis of multiwharf adaptive subtraction method based on L1 norm [D]. Beijing: China University of Geosciences(Beijing), 2012.

[5] 王彦江.多次波压制方法及应用研究[D].北京:中国地质科学院,2009.

Wang Yanjiang. Multiple suppression method and application [D]. Beijing: Chinese Academy of Geological Sciences, 2009.

[6] 李列,谢玉洪,李志娜,等.海上多次波压制与成像方法研究进展[J].地球物理学进展,2015,30(1):446-453.

Li Lie, Xie Yuhong, Li Zhina, et al. Research progress on multiple suppression and imaging methods at sea [J]. Progress in Geophysics, 2015,30(1):446-453.

[7] 石颖,王建民,井洪亮,等.多道自适应匹配滤波方法压制表面多次波[J].地球物理学进展,2013,28(2):785-792.

Shi Ying, Wang Jianmin, Jing Hongliang, et al. Suppressing surface-related multiple by multi-trace adaptive matching filter approach [J]. Progress in Geophysics, 2013,28(2):785-792.

[8] 石颖,邢小林.表面多次波压制的研究进展:回顾与展望[J].地球物理学进展,2011,26(6):2046-2054.

Shi Ying, Xing XiaoLin. Investigation progress on surface-related multiple suppression: Review and outlook [J]. Progress in Geophysics, 2011,26(6):2046-2054.

[9] 刘洪林,张春堂,朱秋影,等.K-L变换在地震资料去噪声的应用[J].东北石油大学学报,2007,31(4):19-21.

Liu Honglin, Zhang Chuntang, Zhu Qiuying, et al. K-L Transform the application of noise in seismic data [J]. Journal of Northeast Petroleum University, 2007,31(4):19-21.

[10] 石颖,陆加敏,柯璇,等.基于GPU并行加速的叠前逆时偏移方法[J].东北石油大学学报,2012,36(4):111-115.

Shi Ying, Lu Jiamin, Ke Xuan, et al. Prestack reverse time migration based on GPU parallel accelerating algorithm [J]. Journal of Northeast Petroleum University, 2012,36(4):111-115.

[11] 石颖,井洪亮,李莹.反馈迭代法压制表面多次波效果分析[J].地球物理学进展,2012,27(4):1493-1500.

Shi Ying, Jing Hongliang, Li Ying. Surface-related multiple suppression effect analysis by feedback iteration approach [J]. Progress in Geophysics, 2012,27(4):1493-1500.

[12] 刘建辉.基于波动理论压制多次波方法研究[D].青岛:中国石油大学,2010.

Liu Jianhui. Research of multiple suppression method based on wave theory [D]. Qingdao: China University of Petroleum, 2010.

[13] 石颖,刘洪,邹振.基于波动方程表面多次波预测与自适应相减方法研究[J].地球物理学报,2010,53(7):1716-1724.

Shi Ying, Liu Hong, Zou Zhen. Surface-related multiples prediction based on wave equation and adaptive subtraction investigation [J]. Geophysics, 2010,53(7):1716-1724.

[14] 赵保宗,孙永清,李学聪.基于波动方程的多次波压制方法应用研究[J].地球物理学进展,2010,25(1):272-281.

Zhao Baozong, Sun Yongqing, Li Xuecong. The progress of the multiple attenuation method based on the wave-equation [J]. Progress in Geophysics, 2010,25(1):272-281.

[15] 陆文凯,骆毅,赵波,等.基于独立分量分析的多次波自适应相减技术[J].地球物理学报,2004,47(5):886-891.

Lu Wenkai, Luo Yi, Zhao Bo, et al. Adaptive multiple wave subtraction using independent component analysis [J]. Geophysics, 2004,47(5):886-891.

[16] 李学聪,刘伊克,常旭,等.均衡多道1范数匹配多次波衰减的方法与应用研究[J].地球物理学报,2010,53(4):963-973.

Li Xuecong, Liu Yike, Chang Xu, et al. The adaptive subtraction of multiple using the equipoise multichannel L1 norm matching [J]. Geophysics, 2010,53(4):963-973.

[17] 董烈乾.基于曲波变换的信噪分离方法研究[D].青岛:中国石油大学(华东),2014.

Dong Lieqian. Research on separation of signal and noise based on curvelet transform [D]. Qingdao: China University of Petroleum(East China), 2014.

[18] 刘琦.基于反射、散射波场分离的多次波消除方法研究[D].长春:吉林大学,2009.

Liu Qi. Multiple elimination study based on wavefields separation between the reflecting and the scattering [D]. Changchun: Jilin University, 2009.

[19] 李唐律.浅海地震资料自由表面多次波压制方法研究[D].青岛:中国海洋大学,2014.

Li Tanglyu. The study on free surface-related multiple attenuation of seismic data in shallow sea [D]. Qingdao: Ocean University of China, 2014.