应用Kubelka-Munk双常数理论的数码转杯纱混色效果预测

徐亚亚， 杨瑞华， 韩瑞叶， 薛 元， 高卫东

(生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

色纺纱是将2种或2种以上的有色纤维经过混合制成的纱线，它使不同颜色或不同性能的纤维通过混合交错并置，在视觉上产生色彩空间混合的效果，使织成的织物呈现出一种独特的彩色效应，富有朦胧的立体效果和质感[1]。织成的织物不需再经染色，既缩短了生产工序，又减少了环境污染，同时提高了企业的经济效益，但由于色纺纱纤维混合一般在前纺工序，受工艺条件的限制，对多品种、小批量、翻改频繁等市场需求，给实际生产管理带来困难[2-3]。数码转杯纺对传统的转杯纺纱机进行了改进，它是将2种及以上不同颜色或不同材料的棉条同时喂入可单独控制的组合式给棉罗拉中，通过控制给棉罗拉的速度来控制喂入量，从而改变所纺纱线的混纺比，最后纺制出所需的色纺纱线。这种纺纱方法可小批量生产，随时更换品种，弥补了传统色纺纱在这方面的缺陷。建立数码转杯纺混色纱以红、黄、蓝三基色进行配色纺纱的配色模型，预测不同混纺比的成纱色彩，是实现数码纺纱工业化进程中计算机智能配色的必要条件之一。

Kubelka-Munk(简称K-M)双常数理论已广泛应用于染料的配方预测中，近年来有许多人利用该理论进行不同纤维材料的混色配方预测研究，并取得了较满意的研究成果。根据以往纤维混色配色研究了解到，求解混色织物中单色纤维的吸收系数K和散射系数S常用的方法有最小二乘法和相对值法。最小二乘法是由Walowit最先提出的利用线性最小二乘回归算法来求解K、S值，使计算值与测量值之间的差异最小；车江宁等利用最小二乘法进行三原色纤维配色的研究，均得到了满意的结果；相对值法是由Burlone提出的用于9种锦纶纤维染色样的配色研究[4-5]。该方法是假设一种纤维的吸收系数和散射系数来求出混色织物中另一种纤维的吸收系数和散射系数[6]。

本文基于K-M双常数理论，利用单色纤维的吸收系数K和散射系数S建立数码转杯色纺纱的混色模型，利用模型对混纺织物的颜色及有色纤维的混合比例进行预测，并计算出色差。利用2种不同的算法求解出各自的K、S值，并对样品颜色及颜色比例进行预测，比较二者对数码转杯纱混色效果的预测准确性，为深入研究数码转杯纺三原色混色模型、计算机智能配色等提供了理论参考。

1 数码转杯纺纺纱原理

三通道异步输入数码转杯纺纱机是一种由电脑系统控制的多组分喂入的转杯纺纱装置。不同于传统转杯纺纱机(见图1)，它具有3个回转自由度的组合式给棉罗拉1、2和3，3个给棉罗拉都是绕同一轴心转动，但每个给棉罗拉都是由电脑程序控制器控制的伺服电动机独立驱动，相互之间不受影响，纺纱时可通过改变3个给棉罗拉的喂入速度来改变棉纤维的喂入量，从而改变多组分纱线的混纺比，因此可将2根或3根不同颜色的粗纱喂入组合式给棉罗拉，经集棉器4和集合给棉罗拉5喂入分梳辊，经过分梳辊的开松、梳理、混合作用，可将多根棉条逐步分解为束纤维并进一步分解为单纤维状，使多色纤维均匀混合，同时还可在高速气流作用下进一步去除棉纤维中的杂质。在分梳辊离心力和气流的作用下，可将连续的单纤维从分梳辊上剥取下来，经输棉通道转移至高速旋转的转杯中。多颜色纤维在纺杯离心力作用下被重新混合并凝聚成须条，经过阻捻器的加捻作用，由引纱罗拉导出形成转杯混纺纱线[7]。

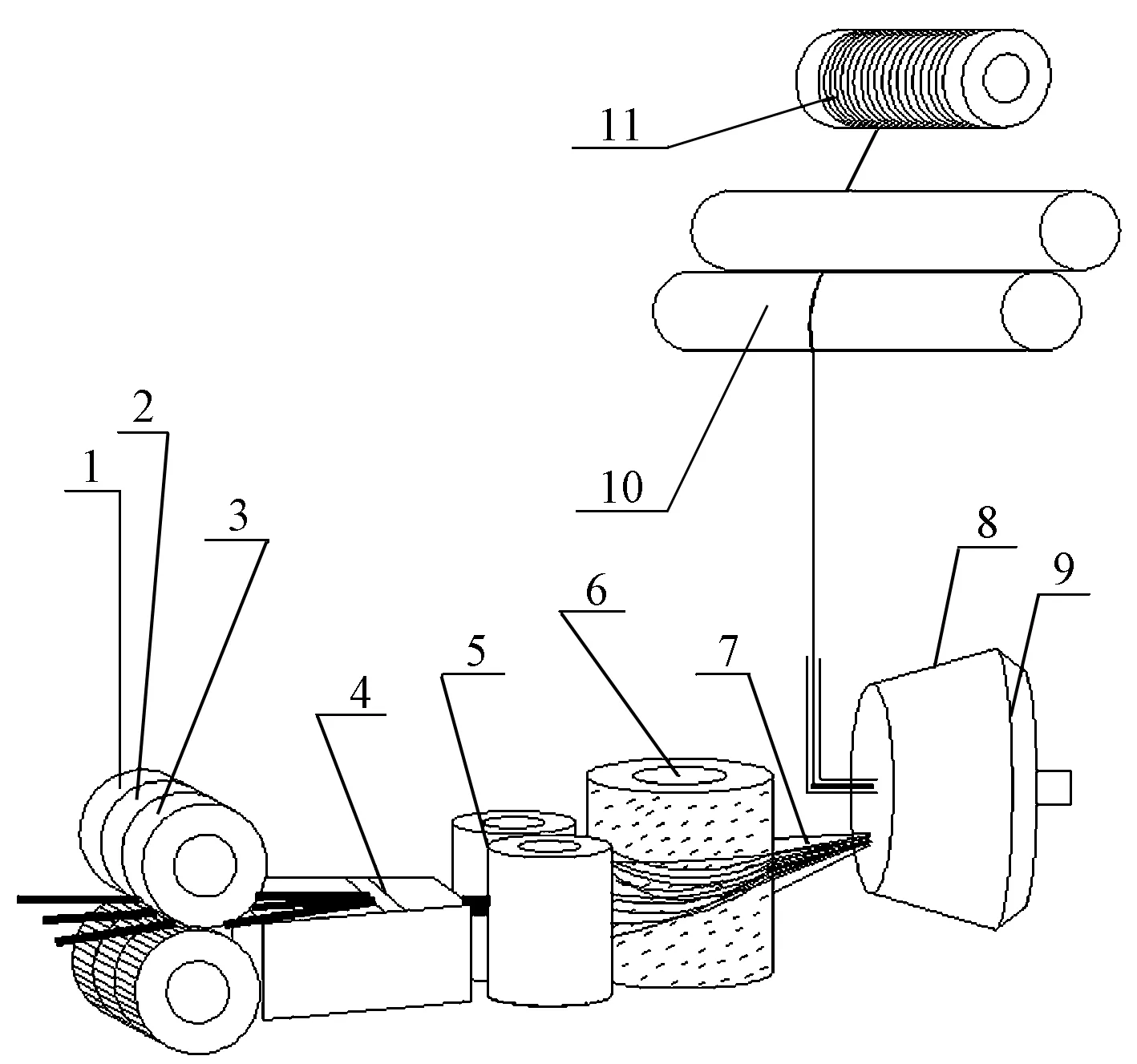
1、2、3—组合式给棉罗拉；4—集棉器；5—集合给棉罗拉；6—分梳辊；7—输棉通道；8—转杯；9—凝聚槽；10—引纱罗拉；11—筒子。图1 数码转杯纺纱机工作流程示意图Fig.1 Working flow chart of digital rotor spinning machine

2 样品的制备及测量

实验原料为红、黄、蓝三原色纯棉粗纱。根据数码转杯纺纱机的工艺原则，将红、黄、蓝3种颜色的棉粗纱按照10%的比例梯度分别纺制两组分和三组分的线密度为44.85 tex的混色纱。样品制备具体比例见表1。

将纺制成的纱线用针织小样机织成织物作为实验样品，其横密为75纵行/(5 cm)，纵密为40横列/(5 cm)。用Datacolor650测色仪测量样品在各波长下的光谱反射率，波长范围为380～700 nm，波长梯度为 10 nm。该实验是在D65标准光源、10°视场下进行测量的，测量孔径为30 mm。为减少实验中产生不必要的误差，测量时将样品折成4层，保证样品不透光，并对同一样品的不同部位进行多次测量，至样品的平均色差小于0.2个CIELab色差单位，取其平均值作为测量值。

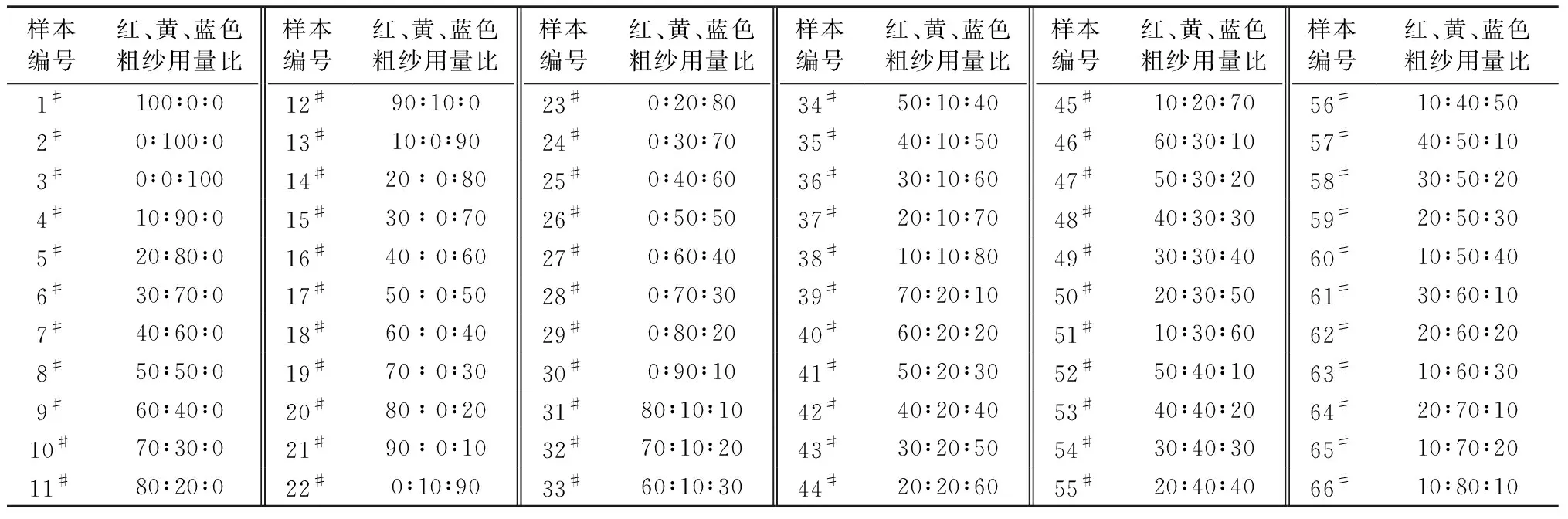
表1 实验样品制备方案Tab.1 Preparation scheme of experimental sample

3 K-M双常数理论模型及验证

3.1 K-M双常数理论

由于反射率与染料质量浓度之间的关系比较复杂，不是简单的线性关系，K-M理论利用吸收系数K和散射系数S这2个常数来简化反射率与染料质量浓度之间的关系。其中反射率R与吸收系数K和散射系数S之间有以下函数关系[8]：

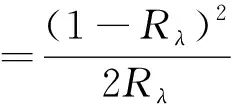
(1)

式中Rλ为样品在一定波长下的反射率。

另外，由于不透明体的吸收系数K和散射系数S都具有加和性，根据K-M双常数理论，混色织物的K/S值与各单色纤维比例之间的关系[9]为

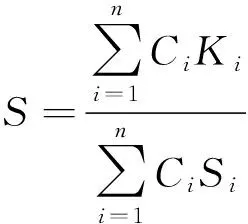
(2)

式中Ci(i=1，2，…，n)为单色纤维在混色织物中所占比例。

3.2 求解K与S值的2种算法

3.2.1最小二乘法

根据K-M双常数理论，对于三组分有色纤维混色，式(2)可表示为

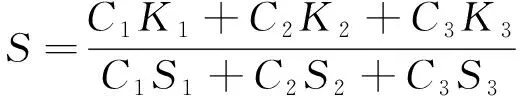
(3)

将方程式展开移项，得

-C1K1-C2K2-C3K3+C1(K/S)S1+

C2(K/S)S2+C3(K/S)S3=0

(4)

根据Walowit提出的最小二乘法，利用系数矩阵求出不同波长下各单色纤维的吸收系数K和散射系数S。

设Am,1=-C1;Am,2=-C2;Am,3=-C3；Am,4=C1(K/S);Am,5=C2(K/S);Am,6=C3(K/S)，可得出系数矩阵：

(5)

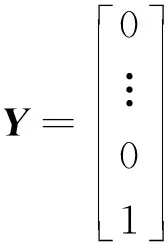
(6)

(7)

因此线性方程组可用矩阵方程表示为

Y=BX

(8)

通过最小二乘法可求出一定波长下各单色纤维的吸收系数K和散射系数S。

X=(BTB)-1BTY

(9)

由于矩阵Y为零矩阵，为保证所求线性方程组有解，将Y矩阵和系数矩阵多加一行1来加以限制，使所求未知数的和或平均值限定为一合理的常数。

3.2.2相对值法

相对值法是选取二组分混合物中其中一种单色纤维，将其散射系数在每个波长处都设为1，即S1=1，则K1=(K/S)1。由于利用相对值法建立模型时所需样本为二组分，因此对于二组分有色纤维混色，式(2)可表示为：

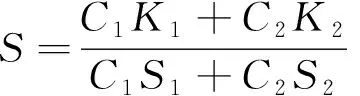
(10)

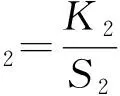
(11)

联立以上2个方程，得：

(12)

K2=(K/S)2S2

(13)

式中：C1、C2为混色织物中单色纤维所占比例；K1、K2、S1、S2为各单色样的K、S值；K/S为混纺织物的K/S值；(K/S)1、 (K/S)2为单色织物的K/S值。

由此可求得一定比例下混合物中另一种纤维的K、S值。为使结果更加准确，可选用不同比例的混色样进行求解，再取其平均值。但是利用这种方法求得的有色纤维的K、S值只是相对值，并非该有色纤维真实的K、S值，因此用这种方法求出的K、S值不能表征该有色纤维的颜色。

3.3 模型验证

根据以上2种方法求得的各单色纤维的K、S值建立各自的基于K-M双常数理论的混色模型，利用这2个模型对混色织物进行配方预测及色差计算，并分析2种算法对数码转杯色纺混色效果预测的准确性。

本文利用最小二乘法求出混色织物中各单色纤维的比例，并做一定的修正，预测混色织物配方。将预测比例与实际比例进行比较，计算每个色样的比例误差，并按照式(14)计算5个色样的平均比例误差[10-11]。

(14)

式中：Δr为实际比例与预测比例之间的比例误差，Xi为预测样本中第i种单色纤维的实际比例，Yi为预测样本中第i种单色纤维的预测比例。

色差计算采用CIELAB色差式，根据预测出的反射率R及已知测量的反射率R通过相关公式转换求出预测样与标准样的色度值L、a、b，并求出二者之间的色差。

4 结果与分析

由于大部分颜色都可利用三原色进行混色来实现，因此为研究三原色纤维的混色效果，在验证样本时利用三组分织物进行模型的验证。为确保验证样本的有效性，求解吸收系数和散射系数的样本不参与模型验证。利用上述2种算法计算出不同波长下三原色纤维的吸收系数K和散射系数S。本文实验制备的单组分及两组分织物共30个全部用于相对值法求解K、S值；三组分织物样本中的31个用于最小二乘法求解K、S值，其余的5个样本用于2种模型的验证，图2、3分别示出利用最小二乘法和相对值法计算出的在不同波长下各单色纤维的K、S值。

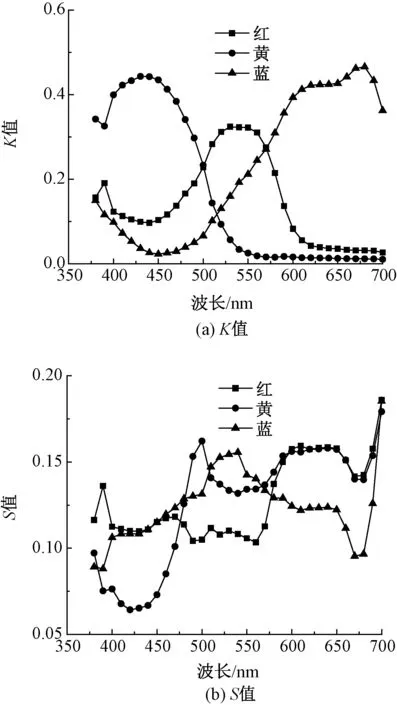
图2 最小二乘法计算三原色纤维的K值和S值Fig.2 K(a) and S(b) values of tricolor fibers calculated by least square method

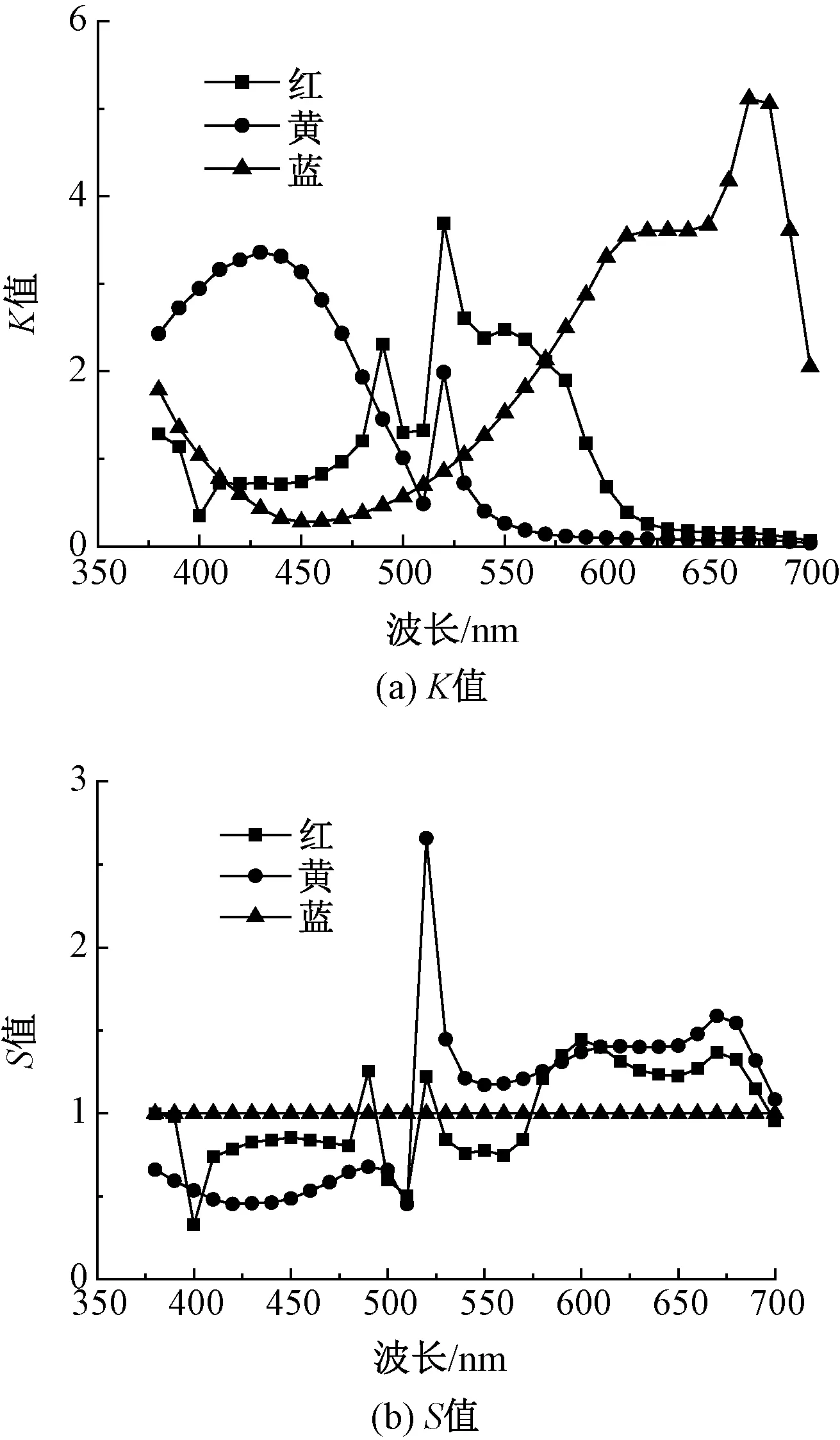
图3 相对值法计算三原色纤维的K值和S值Fig.3 K(a) and S(b) values of tricolor fibers calculated by relative value method

根据以上计算出的不同波长下各单色纤维的K、S值，利用式(15)计算出预测样品的反射率。预测样品的反射率与实际样品的反射率如图4、5所示。样品的实际色度值与预测色度值、实际与预测之间的色差及混色纤维的实际质量比例与预测质量比例见表2、3。

R=1+K/S-[(K/S)2+2×K/S]1/2

(15)

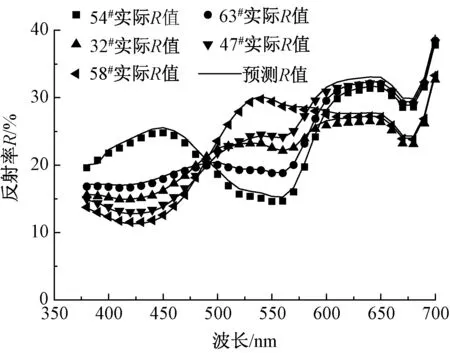
图4 最小二乘法样本实际与预测反射率曲线Fig.4 sample actual versus predicted reflectance curves of least square method

从表2、3可知：利用最小二乘法求得的预测样本的色差在1左右，其平均色差为0.896，平均比例误差为2.84%，预测比例与实际比例较吻合；利用相对值法得出的预测样本的平均色差为1.35，平均比例误差为3.04%。利用相对值法求出的样本的平均色差及平均比例误差均大于利用最小二乘法求出的结果，且由图4、5可看出，利用最小二乘法求得的预测样本的反射率与实际样本的反射率更为吻合，因此，基于K-M双常数理论，利用最小二乘法可很好地预测数码转杯纱的混色效果及混色纤维的比例。

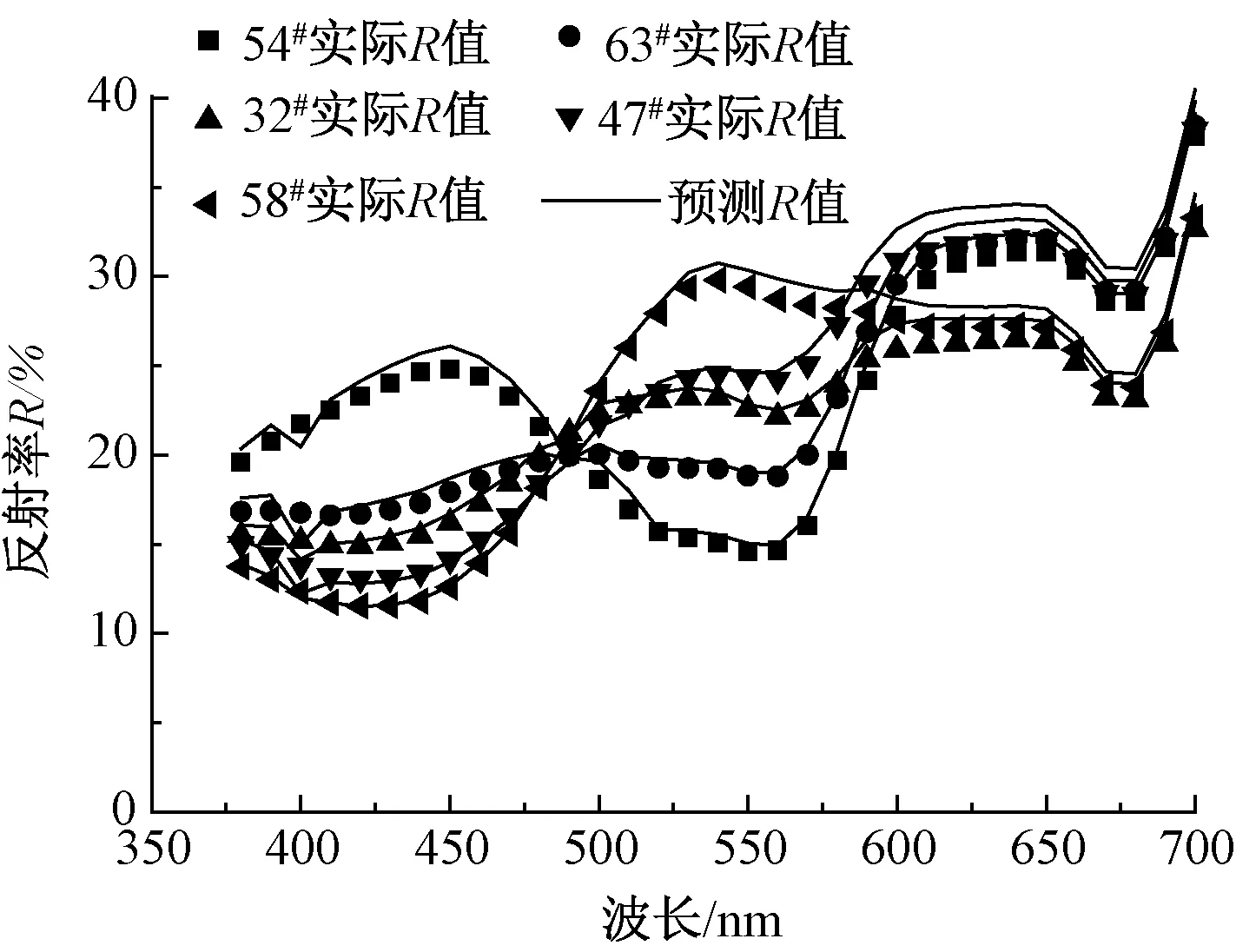
图5 相对值法样本实际与预测反射率曲线Fig.5 Sample actual versus predicted reflectance curves of relative value method

表2 最小二乘法样本参数及混色结果Tab.2 Sample parameters and color mixing results with least square method

表3 相对值法样本参数及配色结果Tab.3 Sample parameters and color mixing results of relative value method

5 结 论

本文研究基于Kubelka-Munk双常数理论来预测数码转杯纱的混色效果，并采用了2种方法来求解单色纤维的吸收系数和散射系数，同时对混色织物的颜色及混色织物中单色纤维的比例进行了预测。通过实际测量及大量的运算结果表明，与相对值法相比，利用最小二乘法可更好地预测数码转杯纱的三原色混色效果及混色纤维的比例。

数码转杯色纺纱独特的混色方法在色纱生产中具有很大的优势，适应市场发展的需求。本文研究的内容及结果为后续数码转杯纺三原色混配色模型构建、计算机智能配色研究及最终投入大规模生产提供了理论参考。

参考文献：

[1] 桂亚夫．浅谈色彩艺术与色纺技术[J]．棉纺织技术，2015(8): 77-80.

GUI Yafu．Discussion on color art and colored spinning technology[J]．Cotton Textile Technology，2015(8): 77-80．

[2] 章友鹤，周建迪，赵连英，等. 色纺纱线生产与工艺技术创新[J]．现代纺织技术，2016，24(5): 61-64．

ZHANG Youhe，ZHOU Jiandi，ZHAO Lianying，et al．Colored spun yarn production and technological innovation[J]．Advanced Textile Technology，2016，24(5): 61-64．

[3] 卫国，张荣庆，姚亚咪．浅析色纺纱的生产实践[J]．现代纺织技术，2013,21(1): 42-45．

WEI Guo，ZHANG Rongqing，YAO Yami．A brief analysis on production practice of colored spun yarn[J]．Advanced Textile Technology，2013,21(1): 42-45．

[4] WALOWIT E．An algorithm for the optimization of kubelka-munk absorption and scattering coeffi-cients[J]．Color Research and Application，1987，12(6): 340-343．

[5] 车江宁，陈东辉．混色纤维双常数库贝尔卡-芒克理论绝对配色[J]．染整技术，2001，23(6): 7-9．

CHE Jiangning，CHEN Donghui．Absolute colour matching of melange fibres using dual-constant kubelka-munk theory[J]．Textile Dyeing and Finishing Journal，2001， 23(6): 7-9．

[6] BURLONE D A．Formulation of blends of precolored nylon fiber[J]．Color Research and Application，1983，8(2): 114-120．

[7] 薛元，高卫东，杨瑞华，等．三棉条异步输入和多级分梳的转杯纺纺纱方法及装置： 105063821A[P]． 2015-11-18．

XUE Yuan，GAO Weidong，YANG Ruihua，et al．Method and device for rotor spinning of three tampon asynchronous input and multi-stage carding: 105063821A[P]. 2015-11-18．

[8] 董振礼，郑宝海，轷桂芬，等．测色与计算机配色[M]．北京: 中国纺织出版社，2007: 141-146．

DONG Zhenli，ZHENG Baohai，HU Guifen，et al．Color Measurement & Its matching Computer[M]．Beijing: China Textile & Apparel Press，2007: 141-146．

[9] DAVIDSON H R，HEMMENDINGER H．Color prediction using the two-constant turbid-media theory[J]．Journal of the Optical Society of America，1966，56(8): 1102-1109．

[10] 周华，王春燕，罗来丽，等．基于Kubelka-Munk双常数理论的纬全显色提花织物配色算法[J]．纺织学报， 2012， 33(5): 35-39．

ZHOU Hua，WANG Chunyan，LUO Laili，et al．Spectrophotometric color matching algorithm of jacquard fabric with all colored wefts based on kubelka-munk double constant theory[J]．Journal of Textile Research，2012，33(5): 35-39．

[11] 许佳艳．涤棉双组份纤维混色计算机辅助配色的研究[D]．杭州:浙江理工大学，2013: 62-63．

XU Jiayan．The study on computer aid matching for colored fiber blends of polyester and cotton[D]． Hangzhou: Zhejiang Sci-Tech University，2013: 62-63．