三维目标位姿跟踪与模型修正

尚 洋，孙晓亮，张跃强，李 由，于起峰

国防科技大学空天科学学院图像测量与视觉导航湖南省重点实验室，湖南 长沙 410072

高效、稳定的目标位姿跟踪技术对于诸多应用领域具有重要意义，如空间应用(交会对接、在轨服务等)、无人机应用(自主降落等)、机器人应用(抓取、装配等)等。基于视觉的位姿跟踪方法具有精度高、自主性强等优势，已成为上述应用中近距离阶段的主要位姿测量手段。基于图像的精密位姿跟踪方法涵盖目标特征提取、参数优化求解等，属于摄影测量与计算机视觉、数字图像处理交叉的摄像测量或图像测量范畴[1]。

研究人员将目标固有的纹理、几何特征用于对位姿参数的精密测量，基本思路是通过建立目标图像2D特征与3D模型之间的对应关系，解算目标位姿参数。双目视觉方法[2]利用双目交会成像理论对目标位姿参数进行测量，相关技术已经较为成熟，且已得到广泛应用。本文关注更为通用、更富挑战的利用单目图像基于目标3D模型的目标精密位姿跟踪方法。

本文开展基于目标3D模型的精密位姿跟踪相关研究，具体内容如下：①已知目标3D精确模型，对于包含丰富直线特征的特殊目标，提出基于直线模型的目标位姿跟踪方法；为处理更为一般目标，提出法向距离迭代加权最小二乘位姿估计方法及距离图迭代最小二乘位姿跟踪方法。②针对目标3D直线模型参数不准确的情况，结合光束法平差思想，提出一种联合优化求解目标位姿及直线参数的方法。③对于包含丰富直线特征的目标，在其3D直线模型完全未知的情况下，利用序列图像信息，在SFM框架下同时实现目标直线模型重建与位姿参数的求解。

1 基于目标3D模型位姿跟踪相关研究现状

针对基于目标3D模型的位姿跟踪问题，本文依据目标3D模型已知与否对相关工作进行梳理。

1.1 目标3D精确模型已知

在已知精确目标3D模型的情况下，基于图像特征，建立2D-3D对应关系即可求解目标位姿参数。广泛采用的方法包含点、直线、边缘轮廓几何结构特征、2D特征描述及深度学习等。

基于点特征的位姿解算即为熟知的“PnP(perspective-n-point)”问题，通过建立n个3D空间点与2D图像点之间的对应关系，求解目标位姿参数。常用的点特征有SIFT[3]、ORB[4]等。对于后续求解，Fischler等[5]对P3P问题进行了研究，并给出了闭式解。对于n≥6的情况，PnP问题存在线性最小二乘解，因此后续研究工作主要集中在n≤5的情况。为提高求解的稳定性及精度，迭代优化求解的策略被引入到PnP问题中，如POSIT[6]算法及正交迭代算法[7]等。点特征较为依赖于目标的纹理信息，易受纹理分布、光照、噪声等因素的影响，算法稳健性不高。

相比于点特征，直线特征包含了更多信息，更有利于实现稳定、精确、可靠的匹配。基于直线对应的位姿测量方法即为被广泛研究的“PnL(Perspective-n-Line)”问题，已有算法可归为以下两类：

(1) 线性求解方法。文献[8]给出了3条直线对应情况下的封闭式解法。文献[9]同样对P3L问题进行了研究，并指出最多存在8个解。文献[10]依据旋转主轴构建局部坐标系，将直线分为3条一组，求解局部坐标系与相机坐标系之间的变换关系，以确定目标位姿参数。文献[11]提出一种直接最小二乘位姿求解方法，通过最小化一个关于姿态矩阵的二次目标函数，得到旋转矩阵的全局最优解。

(2) 非线性优化求解方法。为得到更为精确的位姿参数，一般采用迭代求解方法对线性求解结果进行优化，通常选择像方误差或物方误差构建目标函数。文献[12]提出先迭代求解旋转参数，再线性求解平移参数的方法。文献[13]针对仿射相机模型下的位姿迭代估计方法进行了研究。文献[14]中针对未知模型图像直线对应的情况进行探讨，综合考虑匹配与位姿迭代解算，同时求解直线对应关系和位姿参数。文献[15]通过引入同名点及高程平面约束，实现可靠的航空影像中直线特征匹配。文献[16]将直线特征约束引入到卫星影像区域网平差优化中。

在目标位姿测量中，对目标边缘轮廓进行离散采样是广泛采用的处理思路。文献[17]提出的RAPiD(real-time attitude position determination)是最为研究人员熟知的基于边缘轮廓特征的位姿跟踪算法，其通过对轮廓进行离散采样，沿采样点法向方向搜索匹配点，求解位姿参数。视觉伺服相关方法[18]在视觉伺服的框架下完成位姿跟踪，其在本质上等价于RAPiD算法[19]。为克服RAPiD类方法欠稳健性的缺陷，已有改进可分为以下三类[20]：

(1) 多特征融合：此类方法将其他图像特征同边缘轮廓特征融合，以提高方法的稳健性。关键点特征[21]、纹理特征[22]等被引入提升位姿跟踪的稳健性。

(2) 稳健估计：此类方法在匹配阶段引入稳健估计方法，以剔除误匹配对位姿跟踪算法性能的影响。Drummond等[23]将在最小二乘框架下引入M-估计，通过求解加权最小二乘问题实现位姿跟踪。RANSAC方法被Armstrong等[24]应用于边缘拟合中。

(3) 贝叶斯估计：此类方法主要包含卡尔曼滤波相关方法[25]及粒子滤波相关方法[26]。卡尔曼滤波适用于噪声满足高斯分布假设的情况，粒子滤波更为适用于目标作非线性运动且为非高斯随机过程的情况。

基于边缘轮廓特征的位姿测量方法通过搜索或迭代优化，无须显式提取点、直线，更为稳健、通用。文献[27]对相关工作进行了系统总结，指出最主要的问题集中在几何结构特征的提取与匹配上，易受复杂背景、光照变化、噪声等因素干扰。

2D图像中目标检测与识别领域取得了突出的研究成果，其中涉及的2D特征描述被推广到目标位姿参数的估计中，基本思路是基于虚拟离散位姿参数[28-29]、目标不同侧面[30]等，将针对3D目标的位姿求解问题转换为若干2D图像之间的匹配问题，进而采用2D特征描述建立对应。

基于HOG(histogram of oriented gradient)特征的DPM(deformable parts model)被推广用于目标位姿估计中[30]。文献[28]综合HOG特征、目标结构显著性特征、区域特征及纹理特征等信息，进一步改善匹配结果。基于离散采样视点或目标不同侧面的方法，仅能得到粗略的目标位姿参数。对此，文献[29]将离散采样视点条件下得到的位姿参数估计作为初值，采用MCMC(Markov chain monte carlo)采样方法对位姿参数进一步求精。

2D图像特征描述在定位精度上尚不及点、直线等几何特征，因此，位姿求解精度不高。另外，位姿求解的精度同样受位姿参数离散的粗细粒度的影响。

深度学习已经成为机器视觉、图像处理等领域的热点。相关研究成果也被推广到目标位姿跟踪中，已有应用主要集中在两个方面：①类似于2D特征描述，将学习得到的2D深度特征描述应用于离散位姿参数后的2D图像之间的匹配中[31-32]；②构建卷积神经网络，直接通过2D图像信息预测控制点图像坐标，进而建立2D-3D控制点对应，实现位姿参数的求解[33]。

类似于2D图像特征，深度特征同样存在定位精度不高的缺陷，且位姿参数估计的精度依赖于离散的粒度。另外，深度学习是一项数据驱动的技术，样本数据是决定算法性能的关键因素。

1.2 目标3D模型未知

针对目标3D模型未知的情况，需完全利用图像信息实现目标模型参数与位姿参数的求解。已有相关方法可归为两类：

(1) 利用序列图像(或立体视觉)对目标进行重建，依据重建目标模型，采用绝对定向方法求解目标位姿参数，并利用光束平差方法对结果进行优化。

(2) 将目标模型参数与位姿参数的估计转化为机器人领域中经典的视觉SLAM(simultaneous localization and mapping)问题[34]进行考虑。已有求解方法主要有基于贝叶斯滤波器的方法[35]及基于非线性优化的方法[36]两类。文献[37]基于特征点，在FastSLAM[36]框架下同时求解目标模型参数及位姿参数。

针对模型未知情况下的目标位姿估计问题，当前已公开发表的研究工作相对较少，且已有工作大多基于特征点的思路，对纹理分布、光照变化及噪声等干扰因素的鲁棒性较差。

2 基于目标3D模型的同时位姿跟踪与模型修正方法

开展基于目标3D模型的位姿跟踪研究，分别针对目标3D模型精确已知、不准确及未知的情况提出位姿跟踪与模型修正方法。

2.1 基于目标3D直线模型的位姿跟踪算法

在目标3D直线模型已知的情况下，提出基于目标3D直线模型的位姿跟踪方法，包含基于直线间积分距离度量的位姿跟踪方法及基于多假设直线对应的位姿跟踪方法。

2.1.1 基于直线间积分距离度量的位姿跟踪方法

端点距离导出的直线间相似性度量对直线间断、误差及观测距离等干扰的稳健性较差，影响位姿参数的估计精度。对此，本节提出基于积分距离的直线相似性度量[18]

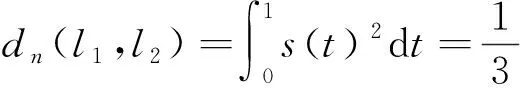
(1)

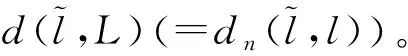
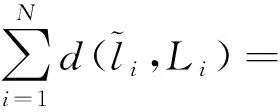
(2)

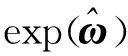
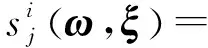
(3)

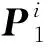
仿真试验模拟卫星位姿跟踪，虚拟相机参数(fx=fy=1 814.8，分辨率640×640，cx=320，cy=320，无像差)。卫星目标模型参数(主立方体尺寸为1000×1000×1000 mm3，太阳能帆板2860×0×557 mm3)。设定目标旋转靠近，沿光轴方向的运动距离为50 m到20 m，采样间隔0.1 s，共得到450帧图像数据，本节方法实现全程稳定跟踪，垂直于光轴方向上位置误差约0.4 mm，沿光轴方向误差约为10 mm，x、y方向上的角度误差约为0.04°，z方向上的角度误差约为0.01°。采用实验室真实场景获取的图像数据对算法进行测试，图1给出部分实物位姿跟踪试验轮廓投影叠加结果，可见本节算法实现了有效跟踪。

图1 基于直线间积分距离度量的位姿跟踪实物试验Fig.1 Experiment results of integral distance between lines based pose tracking

相比于基于端点距离的方法，基于积分距离的直线相似性度量对直线段间断、观测距离等稳健性更好，对位姿参数跟踪的精度更高。

2.1.2 基于多假设直线对应的位姿跟踪方法

基于模型图像直线对应的位姿跟踪方法需先在图像中检测直线，进而建立模型图像直线对应。在杂乱背景干扰或特殊观测条件等不易建立直线对应的情况下，位姿估计的性能将受到影响。对此，本节提出基于多假设直线对应的位姿跟踪方法[20]，为每条模型直线保留多条图像直线对应，在加权最小二乘框架下，通过最小化法向距离实现位姿参数的优化。

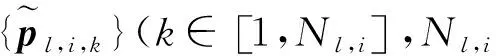
为适应边缘检测中野值点、图像畸变、噪声等因素的影响，采用加权最小二乘方法优化位姿参数，权值由两部分组成：直线约束权值wl(包含拟合误差、直线间距离与夹角)及采样点约束权值wp(包含法向距离、梯度模值与法向)。基于此，采用迭代加权最小二乘方法，通过优化模型直线采样点到图像点的距离，求解目标位姿参数μ，如下式所示

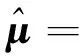
(4)

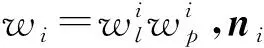
(5)

W为权值矩阵。

仿真试验同基于模型图像直线对应的位姿跟踪方法中设置。本节方法实现全程稳定跟踪，垂直于光轴方向上误差约8 mm，沿光轴方向误差约为70 mm，x、y、z方向上的角度误差分别约为0.5°、0.7°及0.1°。相比于基于模型图像直线对应的位姿跟踪方法，本节算法精度稍差，主要原因是沿法向搜索得到的候选点集为单像素精度。图2给出部分实物位姿跟踪试验轮廓重投影叠加结果，可见本节算法在复杂光照、杂乱背景等情况下都给出了可靠的位姿跟踪结果。

图2 基于多假设直线对应的位姿跟踪实物试验Fig.2 Experiment results of multi-assumption line correspondence based pose tracking

基于多假设直线对应的位姿跟踪方法能够有效适应复杂光照、杂乱背景、特殊视图条件下直线对应错误等情况，表现出了较强的鲁棒性。

2.2 基于目标3D边缘轮廓模型的位姿跟踪方法

为处理更为一般的目标，本节利用目标的轮廓特征，提出法向距离迭代加权最小二乘位姿跟踪方法及距离图迭代最小二乘位姿跟踪方法。

2.2.1 法向距离迭代加权最小二乘位姿跟踪方法

法向距离迭代加权最小二乘位姿跟踪方法[36]通过沿采样点法向一维搜索确定匹配点，采用最小二乘方法迭代寻找一个位姿参数修正量，使得位姿修正后边缘轮廓与图像中轮廓重合。

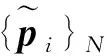
(6)

式中，μ′为位姿参数修正量；Je为描述图像运动与空间运动之间的雅克比矩阵。

为提升方法对杂乱背景、复杂纹理、噪声等因素的稳健性，引入稳健估计ρ(·)及加权策略，针对每一采样点综合考虑法向距离加权w1、候选点数目加权w2、边缘强度加权w3及图像位姿加权w4，最终权值w=w1w2w3w4，则式(6)可改写为

(7)

通过迭代求解上述加权最小二乘问题得到位姿参数的优化结果。

仿真试验模拟卫星位姿跟踪，虚拟相机参数(fx=fy=4 434.33，分辨率764×574，cx=382，cy=287，无像差)。卫星目标模型参数(主立方体尺寸为1000×1000×1000 mm3，太阳能帆板2000×0.5×400 mm3)。设定目标运动从(0，0，30 000，10，30，40)(Tx(mm)，Ty，Tz，Ax(°)，Ay，Az)以速率(0，0，-300,0,0，-1)匀速运动到(0，0，12 900，10，30，-17)，共采集58帧图像，本节方法实现全程稳定跟踪，垂直于光轴方向上误差约6 mm，沿光轴方向误差约为340 mm，x、y、z方向上的角度误差约为1°。图3给出部分实物位姿跟踪试验轮廓重投影叠加结果，可见本节算法给出了正确的位姿跟踪结果。

图3 法向距离迭代加权最小二乘位姿跟踪实物试验Fig.3 Experiment results of normal distance iterative reweighted least squares based pose tracking

2.2.2 距离图迭代最小二乘位姿跟踪方法

基于Chamfer匹配思想，本节提出距离图迭代最小二乘位姿跟踪方法[38]，通过最小二乘方法迭代修正位姿参数，使得模型投影轮廓在距离图中的取值达到最小。

采用Sobel算法对图像进行边缘检测得到边缘图I，距离图DI定义如(8)，每个像素点x的灰度值为其到最近边缘点的欧氏距离，

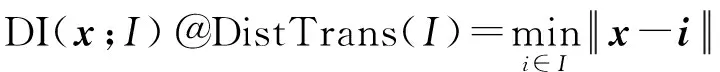
(8)

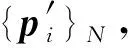
DI(pi)+(DIx(pi),DIy(pi))Je(pi)μ′

(9)

DIx(pi)及DIy(pi)分别为DI在pi处x及y方向上的差分，综合式(8)及式(9)，并引入稳健估计，可得如下最小二乘问题

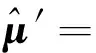
(DIx(pi),DIy(pi))Je(pi)μ′)2)

(10)

迭代求解上述最小二乘问题得到位姿参数的优化结果。

仿真试验中以月球着陆器为对象，模拟着陆过程。着陆器主体结构尺寸约为2×3×3 m3，虚拟相机参数(fx=fy=10 000，分辨率1024×1024，cx=512，cy=512，无像差)，着陆器下落的过程，目标由位姿初始位姿(0，0，53.9，0，0，1)(Tx(m)，Ty，Tz，Ax(°)，Ay，Az)，以(0，0，-0.1，0，0，1)的速度运动到(0，0，48.9，0，0，51)，采集到51帧图像，本节方法实现全程稳定跟踪，垂直于光轴方向上误差约为0.8 m，沿光轴方向上误差约为1 m，x、y方向上的角度误差约为0.7°，z方向上的角度误差约为0.3°。采用兰利发布的多段实物试验视频对算法进行测试，图4给出两段视频中的部分轮廓投影叠加结果，本节方法对着陆器实现了稳定跟踪。

图4 距离图迭代最小二乘位姿跟踪实物试验Fig.4 Experiment results of distance image iterative least squares based pose tracking

本节描述的两种位姿估计方法基于目标边缘轮廓特征，使得对于一般目标的位姿估计成为可能，并在处理过程中引入加权、稳健估计等策略，使得算法对光照变化、复杂背景、纹理等干扰具有较高稳健性。与2.1节中描述的基于直线特征的方法相比，本节方法仅基于单像素精度的匹配点对实现位姿解算，因此算法精度稍差。

2.3 基于目标3D直线模型的同时位姿跟踪与模型修正方法

本节针对目标3D直线模型参数不准确的情况，结合光束法平差的思想，同时优化求解位姿参数及直线模型参数，提出针对序列图像的基于目标3D直线模型的位姿跟踪与模型修正方法。

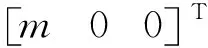
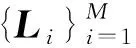
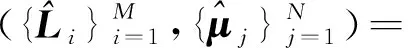
(11)

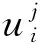
(12)

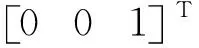
式(11)中待优化参数共有4M+6N个，每条图像直线提供2个约束，N帧图像中共可提供2MN个约束，为完成优化求解，M及N需满足2MN≥4M+6N。

采用卫星仿真图像序列对算法进行测试，仿真参数设置同2.1节，卫星模型包含24条直线，试验中，在模型直线参数中加入随机误差，其中位置误差水平为30 mm，方向误差水平为1°，图像序列长度为36帧，重复100次试验。统计试验结果，模型直线朝向误差约为0.3°，位置误差约为3.5 mm；目标位姿平均角度误差[20]为0.12°，平均位置误差[18]为20.1 mm。另外，模型直线参数修正精度及位姿参数求解精度随着参与优化视图数的增加而提升。

2.4 基于序列图像直线对应的目标结构重建与位姿跟踪方法

针对目标3D直线模型完全未知的情况，本节利用序列图像信息，在SFM框架下实现目标直线模型的重建与位姿参数的求解[20]。

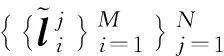
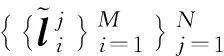
式(11)描述的优化问题具有较多参数，直接进行优化求解，若初值设置不当会造成算法不收敛。对此，本节对式(11)求解前先对部分变量进行优化求解：

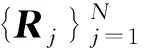
(13)

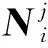
(14)

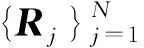
(15)

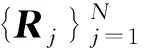
采用仿真图像序列测试算法性能，同2.1节中仿真试验设置，模型直线参数完全未知，本节算法仅基于图像序列完成目标直线模型重建与位姿跟踪。采用LSD[39]算法完成直线特征的提取，相关参数采用文献[37]推荐的设置(scale=0.8，sigma_scale=0.6，quant=2，ang_th=22.5，n_bins=1024，density_th=0.7)。完成在序列长度为36帧情况下，对多次试验结果统计得模型直线朝向及位置误差约为0.4°及7.5 mm；目标位姿平均角度及平均位置误差约为0.16°及23.5 mm。另外，选取一段真实场景拍摄的图像序列，对其中未知模型参数的纸盒目标进行结构重建与位姿跟踪，相机内参数已事先标定。图5(a)给出同名直线匹配结果示例，图5(b)给出目标结构重建与位姿跟踪结果的可视化显示。本节方法准确重建了目标结构，并给出了准确、稳定的位姿跟踪结果。

3 结 论

本文引入机器视觉领域的研究成果，对三维数字摄影测量智能构象基础工作之一——基于目标3D模型的位姿跟踪及模型修正问题进行研究。文中对已有相关工作进行了较为系统地总结，分别针对目标3D模型精确已知、不准确及完全未知的情况下目标位姿跟踪及模型修正问题，依据目标直线、边缘轮廓特征，提出系列处理方法，形成了较为系统、完整的解决方案。

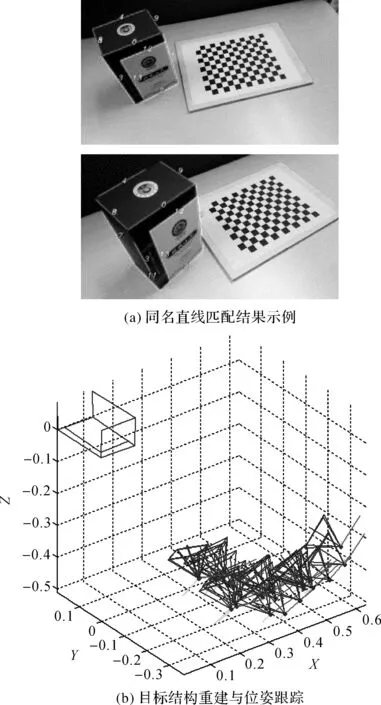
图5 目标结构重建与位姿跟踪试验结果Fig.5 Experiment results of model reconstruction and pose tracking

在目标3D模型精确已知的情况下，基于直线特征的方法在精度方面优于基于一般轮廓特征的方法，其中基于直线间积分距离度量的位姿估计方法在仿真试验条件下，在垂直与沿光轴方向上位置误差分别约为0.4 mm及10 mm，x、y及z方向上的角度误差分别约为0.4°、0.4°及0.1°；但是，基于多假设直线对应的方法对复杂光照、杂乱背景等干扰表现出更强的稳健性，基于一般轮廓特征的方法能够处理结构更为一般的目标；大量实际场景数据试验验证了相关方法能够实现稳定、可靠的位姿跟踪。针对目标3D直线模型不准确的情况，提出同时优化求解模型参数及位姿参数方法，统计多次仿真试验结果，模型直线朝向及位置误差分别约为0.3°及3.5 mm，目标位姿参数平均角度误差及平均位置误差分别约为0.12°及20.1 mm，本文方法实现了可靠跟踪并有效修正了模型参数。对于目标3D模型完全未知的情况，本文提出基于序列图像直线对应的目标重建与位姿跟踪方法，仿真及实际场景数据试验验证了方法能够准确重建目标直线模型并实现可靠位姿跟踪，在多次仿真试验中，重建模型直线朝向及位置误差分别约为0.4°及7.5 mm，位姿参数平均角度及平均位置误差约为0.16°及23.5 mm。

针对进一步的研究工作，可在以下方面进行着重考虑：多特征融合，在同一的框架下合理、综合利用可获取的多种特征，形成互补，提升算法性能。深度学习，可充分挖掘深度学习特征的强大表征能力，用于2D-3D对应的建立；或直接建立端到端的机制，直接由2D图像得到3D位姿参数估计结果；深度学习是数据驱动的技术，为克服训练数据制备的难题，可探索利用目标3D模型仿真构建训练样本。

参考文献：

[1] 于起峰, 尚洋. 摄像测量学原理与应用研究[M]. 北京: 科学出版社, 2009.

YU Qifeng, SHANG Yang. Videometrics: Principles and Researches[M]. Beijing: Science Press, 2009.

[2] 尚洋. 基于视觉的空间目标位置姿态测量方法研究[D]. 长沙: 国防科技大学, 2006.

SHANG Yang. Researches on Vision-based Pose Measurements for Space Target[D]. Changsha: National University of Defense Technology, 2006.

[3] LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[4] RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: An Efficient Alternative to SIFT or SURF[C]∥IEEE International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011: 2564-2571.

[5] FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.

[6] DEMENTHON D F, DAVIS L S. Model-based Object Pose in 25 Lines of Code[J]. International Journal of Computer Vision, 1995, 15(1-2): 123-141.

[7] LU C P, HAGER G D, MJOLSNESS E. Fast and Globally Convergent Pose Estimation from Video Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(6): 610-622.

[8] DHOME M, RICHETIN M, LAPRESTÉ J T, et al. Determination of the Attitude of 3D Objects from a Single Perspective View[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(12): 1265-1278.

[9] CHEN H H. Pose Determination from Line-to-plane Correspondences: Existence Condition and Closed-form Solutions[C]∥IEEE Third International Conference on Computer Vision. Osaka, Japan, Japan: IEEE, 1990: 374-378.

[10] ZHANG Lilian, XU Chi, LEE K M, et al. Robust and Efficient Pose Estimation from Line Correspondences[M]∥LEE K M, MATSUSHITA Y, REHG J M, et al. Computer Vision-ACCV 2012. Berlin, Heidelberg: Springer, 2012: 217-230.

[11] 李鑫, 张跃强, 刘进博, 等. 基于直线段对应的相机位姿估计直接最小二乘法[J]. 光学学报, 2015, 35(6): 615003.

LI Xin, ZHANG Yueqiang, LIU Jinbo, et al. A Direct Least Squares Method for Camera Pose Estimation Based on Straight Line Segment Correspondences[J]. Acta Optica Sinica, 2015, 35(6): 615003.

[12] LIU Y, HUANG T S, FAUGERAS O D. Determination of Camera Location from 2D to 3D Line and Point Correspondences[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(1): 28-37.

[13] CHRISTY S, HORAUD R. Iterative Pose Computation from Line Correspondences[J]. Computer Vision and Image Understanding, 1999, 73(1): 137-144.

[14] DAVID P, DEMENTHON D, DURAISWAMI R, et al. Simultaneous Pose and Correspondence Determination Using Line Features[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Madison, WI: IEEE, 2003: 424-431.

[15] 王竞雪, 宋伟东, 王伟玺. 同名点及高程平面约束的航空影像直线匹配算法[J]. 测绘学报, 2016, 45(1): 87-95. DOI: 10.11947/j.AGCS.2016.20140527.

WANG Jingxue, SONG Weidong, WANG Weixi. Line Matching Algorithm for Aerial Image Based on Corresponding Points and Z-plane Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 87-95. DOI: 10.11947/j.AGCS.2016.20140527.

[16] 曹金山, 龚健雅, 袁修孝. 直线特征约束的高分辨率卫星影像区域网平差方法[J]. 测绘学报, 2015, 44(10): 1100-1107. DOI: 10.11947/j.AGCS.2015.20150023.

CAO Jinshan, GONG Jianya, YUAN Xiuxiao. A Block Adjustment Method of High-resolution Satellite Imagery with Straight Line Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1100-1107. DOI: 10.11947/j.AGCS.2015.20150023.

[17] HARRIS C, STENNETT C. RAPID-A Video Rate Object Tracker[C]∥Proceedings of the British Machine Vision Conference. [s.l.]: BMVA Press, 1990: 73-78.

[18] COMPORT A I, MARCHAND E, PRESSIGOUT M, et al. Real-time Markerless Tracking for Augmented Reality: the Virtual Visual Servoing Framework[J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(4): 615-628.

[19] COMPORT A I, KRAGIC D, MARCHAND E, et al. Robust Real-time Visual Tracking: Comparison, Theoretical Analysis and Performance Evaluation[C]∥IEEE International Conference on Robotics and Automation. Barcelona, Spain: IEEE, 2005: 2841-2846.

[20] 张跃强. 基于直线特征的空间非合作目标位姿视觉测量方法研究[D]. 长沙: 国防科技大学, 2016.

ZHANG Yueqiang. Research on Vision Based Pose Measurement Methods for Space Uncooperative Objects Using Line Features[D]. Changsha: National University of Defense Technology, 2006.

[21] CHOI C, Christensen H I. Real-Time 3D Model-based Tracking Using Edge and Keypoint Features for Robotic Manipulation[C]∥IEEE International Conference on Robotics and Automation. Anchorage, AK: IEEE, 2010: 4048-4055.

[22] BROX T, ROSENHAHN B, GALL J, et al. Combined Region and Motion-Based 3D Tracking of Rigid and Articulated Objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(3): 402-415.

[23] DRUMMOND T, CIPOLLA R. Real-time Tracking of Complex Structures with On-line Camera Calibration[C]∥Proceedings of British Machine Vision Conference. Nottingham: BMVC, 1999: 574-583.

[24] ARMSTRONG M, ZISSERMAN A. Robust Object Tracking[C]∥Proceedings of Second Asian Conference on Computer Vision. Singapore: [s.n.], 1995: 58-62.

[25] YOON Y, KOSAKA A, KAK A C. A New Kalman-filter-based Framework for Fast and Accurate Visual Tracking of Rigid Objects[J]. IEEE Transactions on Robotics, 2008, 24(5): 1238-1251.

[26] CHOI C, CHRISTENSEN H I. Robust 3D Visual Tracking Using Particle Filtering on the SE(3) Group[C]∥IEEE International Conference on Robotics and Automation. Shanghai, China: IEEE, 2011: 4384-4390.

[27] MUNDY J L. Object Recognition in the Geometric Era: A Retrospective[M]∥PONCE J, HEBERT M, SCHMID C, et al. Toward Category-level Object Recognition. Berlin, Heidelberg: Springer, 2010: 3-28.

[28] LIM J J, PIRSIAVASH H, TORRALBA A. Parsing IKEA Objects: Fine Pose Estimation[C]∥IEEE International Conference on Computer Vision. Sydney, NSW, Australia: IEEE, 2014: 2992-2999.

[29] CHOY C B, STARK M, CORBETT-DAVIES S, et al. Enriching Object Detection with 2D-3D Registration and Continuous Viewpoint Estimation[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 2512-2520.

[30] FIDLER S, DICKINSON S J, URTASUN R. 3D Object Detection and Viewpoint Estimation with a Deformable 3D Cuboid Model[C]∥International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: ACM, 2012: 611-619.

[31] MOTTAGHI R, XIANG Yu, SAVARESE S. A Coarse-to-fine Model for 3D Pose Estimation and Sub-Category Recognition[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 418-426.

[32] WOHLHART P, LEPETIT V. Learning Descriptors for Object Recognition and 3D Pose Estimation[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 3109-3118.

[33] CRIVELLARO A, RAD M, VERDIE Y, et al. A Novel Representation of Parts for Accurate 3D Object Detection and Tracking in Monocular Images[C]∥IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 4391-4399.

[34] DISSANAYAKE M W M G, NEWMAN P, CLARK S, et al. A Solution to the Simultaneous Localization and Map Building (Slam) Problem[J]. IEEE Transactions on Robotics and Automation, 2001, 17(3): 229-241.

[35] DAVISON A J, REID I D, MOLTON N D, et al. MonoSLAM: Real-time Single Camera SLAM[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(6): 1052-1067.

[36] KONOLIGE K, AGRAWAL M. FrameSLAM: From Bundle Adjustment to Real-time Visual Mapping[J]. IEEE Transactions on Robotics, 2008, 24(5): 1066-1077.

[37] AUGENSTEIN S. Monocular Pose and Shape Estimation of Moving Targets, for Autonomous Rendezvous and Docking[D]. Stanford, CA: Stanford University, 2011.

[38] 李由. 基于轮廓和边缘的空间非合作目标视觉跟踪[D]. 长沙: 国防科技大学, 2013.

LI You. Contour and Edge-based Visual Tracking of Non-cooperative Space Targets[D]. Changsha: National University of Defense Technology, 2013.

[39] VON GIOI R G, JAKUBOWICZ J, MOREL J M, et al. LSD: A Fast Line Segment Detector with a False Detection Control[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(4): 722-732.