巧画图，妙解题

☉江苏省南京航空航天大学附属高级中学 吴如光

我们知道，熟知的函数、立几、解几等知识板块经常会用到画图的方法.其实，“画图”还能用来处理和解决很多其他的数学问题，是一种很有价值的数学方法，但有时很多考生并未给予足够的重视.本文通过实例，展示“画图”这个技能是如何处理与解决除函数、立几、解几等知识板块外的其他各类高考数学问题，正确让考生熟悉并掌握这个新技能，为高考加分！

一、画图解决集合问题

学好集合知识，必须充分理解和掌握好数学语言，特别是数形结合思想.会用简约、准确的数学图形语言（表格、韦恩图、数轴等）来转换相关的集合问题，是数学的基本能力之一，也是数形结合思想在集合解题中的充分体现.集合中常用的方法是数轴法和Venn图法.

例1 （2016年苏州一模）已知集合A＝{x|x＜-1或x≥1}，B＝{x|2a＜x＜a＋1，a＜1}，若B⊆A，则实数a的取值范围为______.

分析：根据集合A、B之间的关系B⊆A，数形结合画出相应的数轴.解此类题要注意是否包括端点临界值.

解：因为a＜1，所以2a＜a＋1，所以B≠∅，画出数轴分析，如图1所示.

图1

由图知要使B⊆A，需2a≥1或a＋1≤-1，即a≥或a≤-2.又因为a＜1，所以实数a的取值范围是（-∞，-2］∪[，1）.

解题思想：集合问题大都比较抽象，解题时要尽可能借助Venn图、数轴等工具，利用数形结合思想将抽象问题直观化、形象化、明朗化，从而使问题获解.

二、画图解决三角函数问题

对于一些含有三角函数背景的填空题，若能以函数作出图像，以图像结合性质，以性质反馈问题，则能有效地掌握技巧，快捷地处理相关的三角函数问题，得出正确的答案.数形结合思想体现在三角函数中是利用单位圆中的三角函数线、三角函数图像求三角函数的定义域、解三角不等式、求单调区间、讨论方程实根的个数、比较大小等问题的解决.

例2（2015年上海卷）已知函数f（x）=sinx，若存在x1，x2，…，xm满足0≤x1＜x2＜…＜xm≤6π，且|f（x1）-f（x2）|+|f（x2）-f（x3）|+…+|f（xm-1）-f（xm）|=12（m≥2，m∈N*），则m的最小值为______.

分析：根据相应的三角函数问题加以转化，通过数形结合，利用函数的图像和已知条件加以直观分析与处理.

解：对任意的xi，xj，|f（xi）-f（xj）|≤f（x）max-f（x）min=2，欲使m取得最小值，尽可能多地让xi（i=1，2，…，m）取最值点，考虑到0≤x1＜x2＜…＜xm≤6π，|f（x1）-f（x2）|+|f（x2）-f（x3）|+…+|f（xm-1）-f（xm）|=12（m≥2，m∈N*），按照图2所示的取值可以满足条件，所以m的最小值为8.

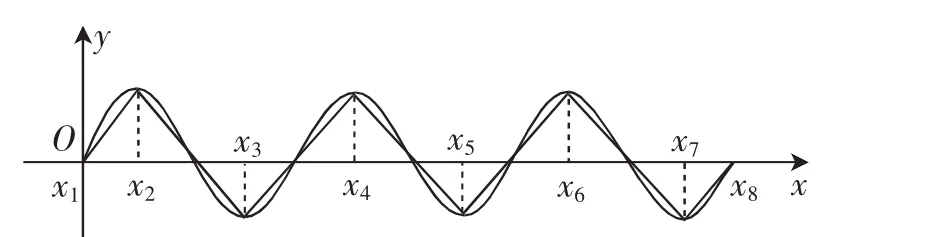
图2

解题思想：涉及三角函数的性质的问题，同时还涉及绝对值及其应用，解决问题的关键是通过数形结合思维，直观来分析与处理，省去不必要的推理、分析及繁杂的运算，有效地解决了有关三角函数的性质问题.

三、画图解决平面向量问题

在平面向量中，平面向量的线性运算自身蕴含着丰富深刻的几何背景，平面向量的坐标表示使平面向量问题代数化成为了可能.平面向量知识成为数形结合中重要的载体，是数形结合对应的高度统一的实例之一.

例3 （2015年北京卷理13）在△ABC中，点M，N满则x=______，y=______.

分析：通过特殊化，并结合构造平面直角坐标系，作出图像数形结合，利用向量的坐标运算来求解相应的参数值问题.

解：不妨设AC⊥AB，且AB=4，AC=3，以A为坐标原点，AB、AC所在直线分别为x轴、y轴建立直角坐标系A-xy，如图3，则A（0，0），B（4，0），C（0，3），M（0，2），N（ 2，）.

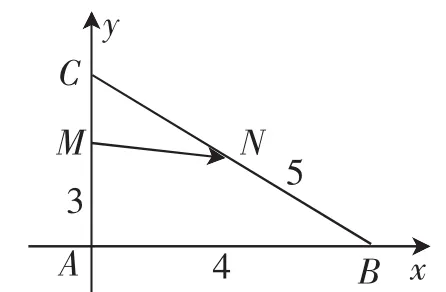
图3

解题思想：在解决平面向量问题中，通过巧妙构造坐标系，利用坐标法来求解相应的向量问题，也是高考中比较常见的一类技巧方法.巧妙通过坐标系的建立，把平面向量的线性运算问题转化为坐标运算问题，数形结合，利用函数、三角函数或不等式来求解最值问题，思路清晰，解法巧妙.

四、画图解决算法问题

算法的程序框图本身就是以流程图来叙述数学问题，在解决此类问题时要熟练掌握程序框图中所表示的意义，通过数形结合，利用函数、数列、不等式等相关知识来分析与处理.

例4（2014年四川卷）执行如图4所示的程序框图，如果输入的x，y∈R，那么输出的S的最大值为（ ）.

A.0 B.1

C.2 D.3

分析：结合算法的程序框图，其求解的是不等式组条件下S＝2x＋y的所有取值与1中的最大值，通过数形结合来分析与求解.

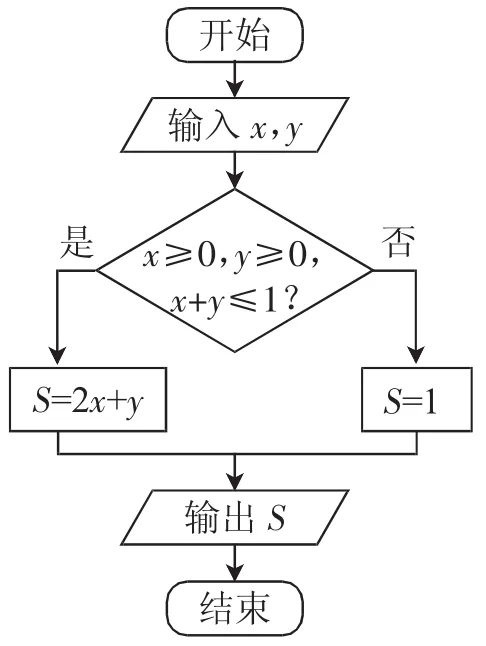
图4

解：题中程序输出的是在不等式组S＝2x＋y的最大值与1中较大的数，结合不等式组对应的可行域（如图5所示），可知当x＝1，y＝0时，S＝2x＋y取得最大值2，而2＞1，故选C.

解题思想：此类问题往往综合了算法初步知识，以数形结合的形式来展示函数中的分段函数问题，以及基本不等式的应用等，通过多个知识点的交汇与综合来创新问题，达到考查能力与应用的目的.

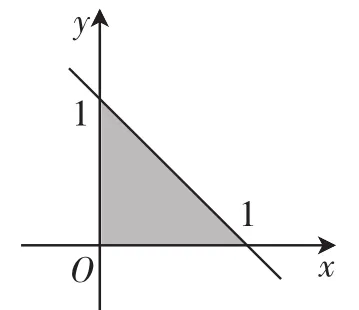
图5

五、画图解决概率问题

许多概率问题都可以通过画树形图、建立直角坐标平面等，将数的问题转化为形的问题，借助于形的优势，使问题得到解决.特别在几何概型中，数形结合显得尤为重要.

例5 （2016年全国卷Ⅰ理4）某公司的班车在7：30，8：00，8：30发车，小明在7：50至8：30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（ ）.

分析：根据题目条件，画出时间轴，结合时间轴的长度加以数形结合，利用长度的计算来确定几何概型问题.

解：如图6所示，画出时间轴.

图6

小明到达的时间会随机地落在图中的线段AB上，而当他的到达时间落在线段AC或DB时，才能保证他等车的时间不超过10分钟，根据几何概型可得所求的概率

解题思想：涉及概率的求解问题，有时可以把古典概型、几何概型的问题转化为直观图形，通过数形结合来分析显得更为直观与快捷.特别地，解决以实际问题为背景的几何概型时，往往先确定几何概型中的类型，作出相应的图像，并结合长度、区间、面积、体积等的计算来求解相应的概率.

六、画图解决不等式问题

在求解一些不等式问题时，特别是绝对值不等式问题，往往可以通过转化，结合函数的图像加以数形结合，可以直观快捷地处理不等式的求解问题.

例6（2016年日照一模）已知不等式|x-2|+|x-5|＜a有解，则实数a的取值范围为______.

分析：直接求解含有参数的绝对值不等式问题，比较难下手，通过引入函数，结合函数的图像直观分析，数形结合就比较简单易操作.

解：设函数f（x）=|x-2|+|x-5|=a，在同一直角坐标系中画出两函数图像（如图7），函数f（x）的最小值为3，要使原不等式有解，必须且只须a＞3，故所求实数a的取值范围为（3，+∞）.

解题思想：运用函数思想与数形结合思想解决不等式问题，而运用数形结合思想来处理不等式问题的关键是认识相关知识的本质与函数的关系，同时熟悉相应函数的性质，以及相应函数图形的应用.

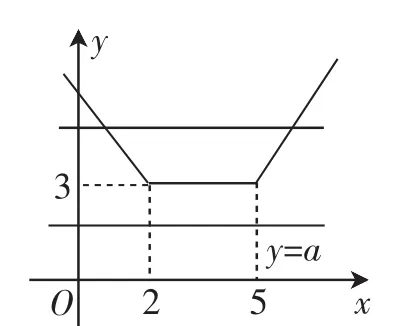
图7

七、画图解决解三角形问题

对于解三角形的问题，往往要与直观图形加以数形结合，设法将已知与所求的边角都凑到或转移到一个三角形之中，才利于发现关系与找到求解的办法.特别地，对于解三角形时所遇到的实际问题中求高的问题较多，且多数题都是需要通过利用一个斜三角形与一个直角三角形才可求出山高、塔高、烟囱高等.

例7 （2016年南通一模）在△ABC中，已知AB=4，AC=7，AD是BC边上的中线，且AD=，试求边BC的长.

分析：通过设元，数形结合，综合利用△ABC与△ABD的公共角B，由余弦定理列出方程，从而得以求解相应的边长.

解：设BD=x，则在△ABD中，由余弦定理，得

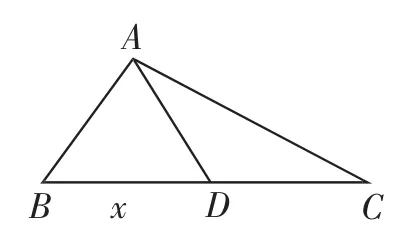
图8

解题思想：在解决三角形的相应问题中，往往通过三角形直观图形加以数形结合，可以利用不同三角形中的公共元素，结合方程思想，往往可以收到意想不到的效果，方便快捷地处理相应问题.

八、画图解决逻辑问题

对于充要条件的判定，一判断充分性，二判断必要性，要明确题中哪个作条件，哪个作结论，若p⇒q，则p是q的充分条件，q是p的心要条件.特别地，当涉及集合关系、立体几何等相关问题时，可以通过数形结合来直观分析，快捷简单.

例8（2016年温州质量检测）设集合A、B是全集U的两个子集，则“A⊂B”是“UA∪B=U”的（ ）.

A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分也不必要条件

分析：如果直接根据两个集合之间的关系加以判断命题之间的对应逻辑关系，往往容易忽视相应集合的一些特殊问题，这也是很多学生容易犯错误的地方.而若结合图形加以直观分析，更加明了，更加易于掌握.

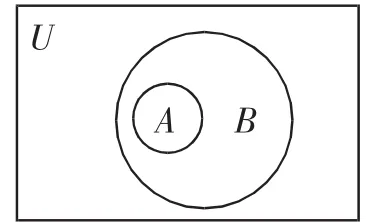
图9

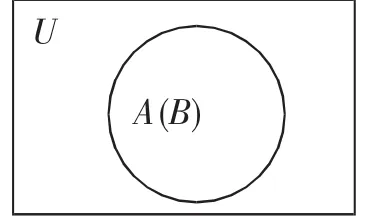
图10

解：如图9，当A⊂B时，UA∪B=U成立；如图10，当A=B时，UA∪B=UB∪B=U也成立，即UA∪B=U成立时，可得A⊆B.

所以“A⊂B”是“UA∪B=U”的充分不必要条件，故选A.

解题思想：数形结合的思想是数学重要的思想方法之一，其具有直观性、灵活性、深刻性，并有跨越各知识点的界线，有较强的综合性.常用逻辑用语部分主要体现在判断充要条件时可转化为集合问题，利用数轴、图形等进行数形结合分析求解.

巧妙运用“画图”这一数形结合的思想方法解决一些抽象的数学问题，可起到事半功倍的效果，数形结合的重点是研究“以形助数”.数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，是中学数学中几种重要的数学思想之一，尤其在解决选择题、填空题时发挥着奇特功效，大大提高了解题能力与速度.F