多种角度齐切入，平面向量巧求解——一道模拟题的多解剖析

☉江苏省宿迁中学 李 青

美国著名数学家哈尔莫斯曾说过：“问题是数学的心脏.”对学生来说，各类试题无疑是最熟悉的一个“问题”.如何提升学生的解题能力，是每位老师思考的重要课题.经过理论和教学实践证明，一题多解是提高解题能力的有效途径.在呈现不同解法的同时，暴露思维过程，得以拓展与提升.

例题 （2018届江苏省南通、扬州、泰州、淮安、徐州、宿迁二模第13题）在平面四边形ABCD中，已知AB=1，BC=4，CD=2，DA=3，则A →C·B →D的值为______.

分析：平面向量的数量积问题一直是高考题、各类模拟题中的常见题型，涉及数量积的求解、最值的确定、参数的求值等问题，且往往难度较大.从哪些角度切入，如何正确破解此类问题，是处理此类问题的重点所在.

思路分析1：基底法1

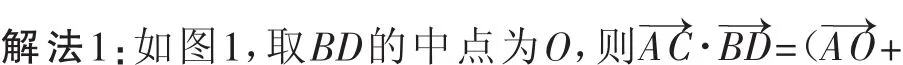
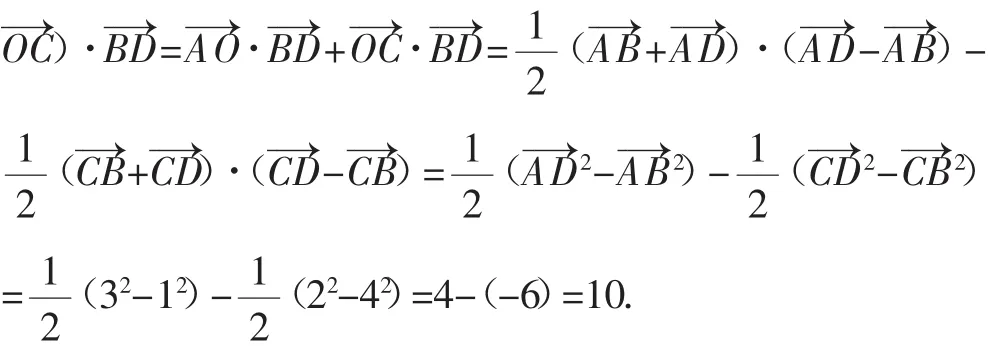
故填答案：10.

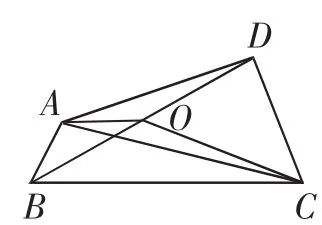
图1

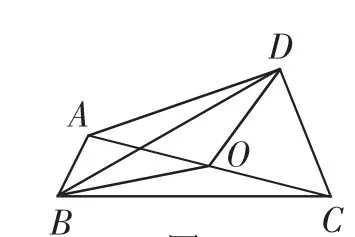
图2

思路分析2：基底法2

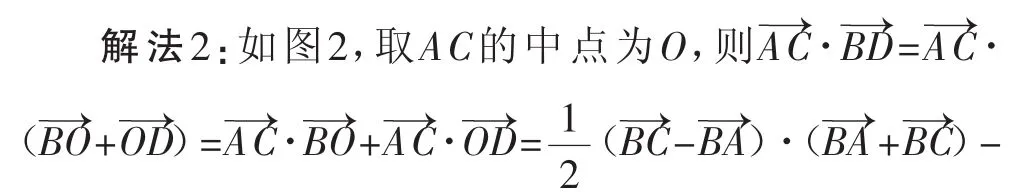
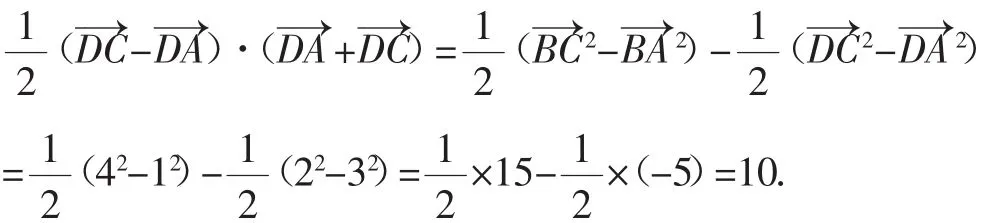
故填答案：10.

思路分析3：余弦定理的向量式法

故填答案：10.

思路分析4：余弦定理法

解法4：在△ABC与△ADC中，根据余弦定理可得AC2=AB2+BC2-2AB·BC·cosB=AD2+CD2-2AD·CD·cosD，整理可得2cosB-3cosD=1.

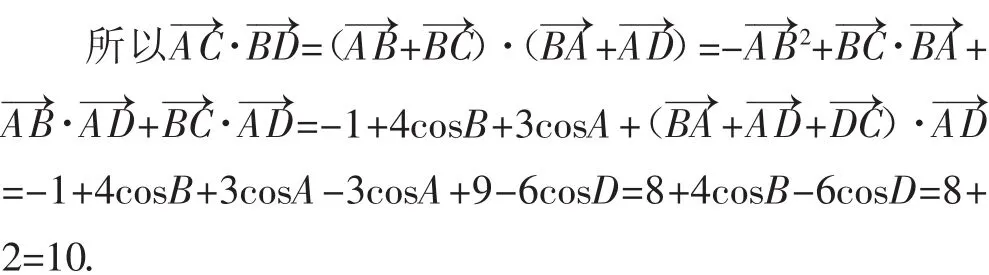
故填答案：10.

思路分析5：一般建系法

解法5：如图3，以A为坐标原点，AB所在直线为x轴建立平面直角坐标系. 设C（x1，y1），D（x2，

图3

将②式展开，把①和③式代入整理可得=x1x2-x1+y1y2=10.

故填答案：10.

思路分析6：特殊建系法

解法6：取特殊情况∠ABC=90°，建立如图4所示的平面直角坐标系，可知B（0，0），A（0，1），C（4，0），此时设点D（m，n）为⊙A与⊙C在第一象限内的交点.

图4

而⊙A：x2+（y-1）2=9，⊙C：（x-4）2+y2=4，把两圆方程对应相减并整理可得4x-y=10. 而=（4，-1），=（m，n），则有（4，-1）·（m，n）=4m-n=10.

故填答案：10.

思路分析7：极端思维法1——解三角形

解法7：由于AB=1，BC=4，CD=2，DA=3，取极端情况（B、A、D三点共线，如图5，构成等腰△BCD），此时BC=BD=4.由余弦定=1 ×4 ×cos180°+4 ×4 ×cosB=4×（-1）+16×=10.

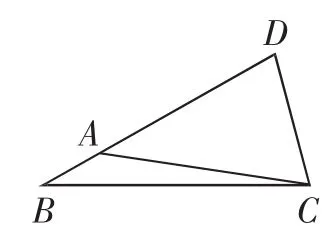
图5

故填答案：10.

思路分析8：极端思维法2——四点共线

解法8：由于AB=1，BC=4，CD=2，DA=3，取极端情况（A、B、C、D四点共线），此时A（0，0），B（1，0），C（5，0），D（3，0），使其满足以上条件，此时A →C=（5，0），B →D=（2，0），则有A →C·B →D=5×2+0×0=10.

故填答案：10.

点评：根据解法1与解法2的分析可知，在平面四边形ABCD中，恒有成 立 ，结合其中一条对角线的中点，利用平面向量的中点公式加以转化，结合基底法来处理是解决此类问题的最常见思维；而解法3与解法4分别通过余弦定理的向量式与余弦定理来转化，借助角，设出不求，达到求解的目的；而解法5与解法6通过建立平面直角坐标系，平面向量的坐标运算来处理也是常见解法，解法5的一般建系法，建系后计算比较复杂，而解法6通过特殊建系法，并结合两圆公共弦所在直线的求解进行转化与处理，运算相对来说简单一点；特别是解法7与解法8的极端思维法，结合特殊的三角形或特殊线段来处理，有时可以达到“秒杀”的效果.

通过一题多解，我们尝试到：这样的问题可以使我们的解题思路开阔，妙法顿生，提高了解题速度，培养了发散思维能力，有助于激发我们学习的主动性、积极性、趣味性，从而全面提高我们的知识水平和思维广阔性，提升数学素养.F