干湿循环效应下石灰处治膨胀土动力特性试验研究

莫文瑜，农承尚

0 引言

广西是我国最典型的膨胀土地区之一，其中以南宁、百色等四市和宁明、田阳等五县分布最广[1]。随着广西高速公路建设的发展，修筑高速公路这样巨型带状工程时，不可避免地会穿越膨胀土地区。在土中添加石灰是常见的膨胀土土性改良方法，经处治后的膨胀土物理力学性质得到明显增强。广西地处亚热带，具有明显的湿热多雨的气候特征，而膨胀土的工程特性随着外界气候环境因素变化会发生显著的变化。若石灰处治膨胀土作为路基填料暴露在大气营力中，尤其是填方路堤，其土体三面临空而形成梯形风化程度分布带，必然受到气候环境因素的长期作用，强度比刚竣工时会明显下降。

本文的试验对象是石灰处治膨胀土，作为路基填料，长期承受交通荷载的反复影响，若强度不足会产生诸如翻泥冒浆、侧向挤出和不均匀沉降等现象。研究石灰处治膨胀土在气候因素特别是干湿循环作用下的动力特性十分有必要，对合理有效地进行路堤边坡防护、路面结构设计和养护具指导意义。本文主要依托高速公路膨胀土路堤处治工程建设项目，用伺服电机控制式动三轴试验系统(DYNTTS)对干湿循环效应下石灰处治膨胀土的动应力动应变特性，动弹模量、阻尼比的变化规律等动力特征进行研究。

1 膨胀土改性试验

石灰处治膨胀土的处治效果主要受配土方式、掺灰率、闷料时间、控制含水率等因素影响，参考前人研究[2-3]，结合本文依托的公路路堤处治项目，本文室内试验所用的石灰处治膨胀土制样指标如表1所示，压实度为干法重型击实试验所确定的处治土最大干密度的95%；制样含水量比最优含水率大2%～3%，取为19%；掺灰比为6%。将重塑膨胀土和石灰处治膨胀土进行一系列室内物理力学试验，各项物理力学指标如表2、表3所示。

表1 石灰处治膨胀土制样指标表

膨胀土经石灰处治之后，表现出粉土的性质，抗剪强度有着大幅度的提高，压缩特性增强，胀缩性被抑制，土的物理力学特性明显增强，改性效果非常明显。

表2 基本物理性质指标表

表3 力学指标表

2 干湿循环效应下石灰土动力响应特征分析

2.1 土动本构模型—等效线性模型(Hardin-Drnevich模型)

对土的动变形特性进行研究，主要目的是获得土体的动应力应变关系，即动本构关系，动弹性模量与动应变关系以及阻尼比与动应变关系等。动弹性模量与阻尼比是表现土体动力特性的主要指标，前者反映了土体抵抗动荷载的能力，后者则代表土体振动时能量衰减的大小。目前表现土体动本构关系的模型很多，通常采用的模型是经验模型，其代表类模型为Masing类模型，它以经验性的非线性骨架曲线和Masing准则为基础，从多角度、以多种方法描述了土体的动应力动应变特性。Hardin[4]等人提出的Hardin-Drnevich模型就是典型的Masing类模型之一，该模型把土视为粘弹性体，将滞回特性用阻尼比与动应变的关系(λ～εd)来表达，将骨干曲线的特性用动弹模量与动应变的关系(Ed～εd)来表达，不追求滞回曲线和骨干曲线的具体数学表达式，采用等效动弹模量Ed和等效阻尼比这两个参数来表达土动本构关系的特征。

Hardin等人由试验得出土在周期循环荷载作用下的动应力动应变关系曲线为双曲线型：

(1)

式中，Edmax、σdmax分别为最大轴向动弹模量和最大轴向动应力。

本文采用Hardin-Drnevich模型分析石灰处治膨胀土的动应力动应变关系。令A=1/Edmax、B=σdmax，代入式(1)中有：

(2)

即：

成也萧何，“祸”也萧何，奥巴马曾因雄辩口才入主白宫，却又因麦克风陷入“失言”危机，而这并非是他的第一次教训。

(3)

式中，A、B为试验所获得的参数。

在经过试验后可获得1/Ed～εd关系曲线，通过拟合计算可以确定Edmax。

在假定材料符合线弹性关系的前提下，Hardin等人还推导出阻尼比和动弹模量的关系，可计算全应变范围内的阻尼比，本文的λ～εd关系曲线根据该公式计算绘制：

(4)

式中，λmax可以根据经验公式和试验确定两种方式获取，由于经验公式对土类的局限性，在本文中无法直接引用，故在本文的试验中，计算出全应变范围内的阻尼比后，在εd>0.03%时，λ～εd曲线开始趋于平缓，取趋于常数的λ值作为该状态下的最大阻尼比λmax。

2.2 动三轴试验方案简介

本次试验在GDS公司的伺服电机控制式动三轴试验系统(DYNTTS)上进行，该系统可通过模拟正弦波、方波、三角波等动态波形，完成对试样动应变、动应力、动弹模量及阻尼比等土体动态指标的测试。影响土体动力性能的因素非常多[5]，本次试验主要考虑的因素有：围压、固结比、振动频率、干湿循环次数、动应力幅值以及振动周期次数等。

动应力选择以能显示动应力-应变关系曲线的形式为基本要求，幅值以不超过高速铁路路基表层的动应力幅值为限，高速铁路路基表层动应力不超过100 kPa[7]，采用等差逐级加载动应力的方式加载；一般来说，三轴试验围压不应小于土层上覆压力，不应大于土体实际承受的最大有效应力，车辆荷载作用下路基工作区深度主要在0.8 m～2.0 m之间[6]，考虑到路基工作区深度较浅，本次试验的固结比以1.0为主；车辆荷载作用下对路基造成的振动频率较复杂，振动频率的构成随车辆工况变化而变化，根据实测基床动应力频谱资料，对路基影响最大的是基频[8]，根据徐毅在连盐高速公路开展的现场试验[6]，其两个测点在车辆荷载影响下的振动频率主要集中在3～30 Hz，受车速的影响较小，但小车引起的振动频率明显高于大车，受限于试验仪器，本次试验主要采用的振动频率为5 Hz。

2.3 骨干曲线(动应力-应变关系曲线)变化规律

经历不同干湿循环次数和不同围压下的石灰处治膨胀土在循环荷载作用下的骨干曲线如图1所示(振动频率为f=5 Hz，固结比Kc=1.0)。

(a)围压σ3c=50 kPa时的骨干曲线图

(b)围压σ3c=100 kPa时的骨干曲线图

(c)围压σ3c=150 kPa时的骨干曲线图

(d)围压σ3c=200 kPa时的骨干曲线图

根据图1可知，同围压条件下，当动应变一定时，干湿循环次数越多动应力越小，试样强度越低；当动应力一定时，干湿循环次数越多动应变越大，说明试样的刚度越小。同围压下的试样动应力水平有所降低，可以认为随着干湿循环次数的增加，试样抵抗动载的能力逐渐衰减，第1次与第2次干湿循环后动应力水平衰减幅度较大，第3次干湿循环后动应力水平衰减幅度减缓，并逐渐趋于稳定。

2.4 动弹模量变化规律

经历不同干湿循环次数和不同围压下的石灰处治膨胀土在循环荷载作用下的Ed～εd关系曲线如图2所示，1/Ed～εd关系曲线如图3所示(振动频率为f=5 Hz，固结比Kc=1.0)。

(a)围压σ3c=50 kPa时的Ed～εd关系曲线图

(b)围压σ3c=100 kPa时的Ed～εd关系曲线图

(c)围压σ3c=150 kPa时的Ed～εd关系曲线图

(d)围压σ3c=200 kPa时的Ed～εd关系曲线图

(a)围压σ3c=50 kPa时的1/Ed～εd关系曲线图

(b)围压σ3c=100 kPa时的1/Ed～εd关系曲线图

(c)围压σ3c=150 kPa时的1/Ed～εd关系曲线图

根据图2、图3可知，同围压条件，相同动应变下，随着干湿循环次数的增加，试样的动弹模量越小，初始动弹模量也越小；相同动弹模量下，干湿循环次数越多，试样的动应变越小，均说明试样抵抗动荷载的能力随干湿循环次数的增加而降低。从曲线变化规律来看，试样的动弹模量和初始动弹模量随着干湿循环次数的增加而不断衰减，第1次与第2次干湿循环后动弹模量衰减幅度较大，第3次干湿循环后动弹模量衰减幅度减缓，并逐渐趋于稳定。但因初始动弹模量衰减较为明显，当次循环对应的动弹模量衰减幅度越来越小。

2.5 阻尼比变化规律

经历不同干湿循环次数和不同围压下的石灰处治膨胀土在循环荷载作用下的λ～εd关系曲线如图4所示(振动频率为f=5 Hz，固结比Kc=1.0)。

(a)围压σ3c=50 kPa时的λ～εd关系曲线图

(b)围压σ3c=100 kPa时的λ～εd关系曲线图

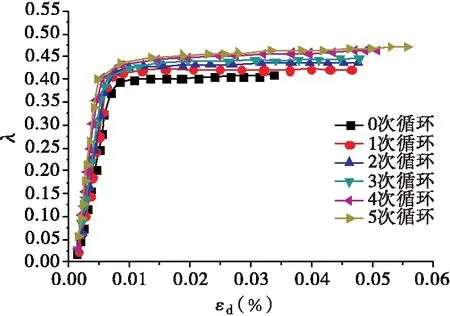
(c)围压σ3c=150 kPa时的λ～εd关系曲线图

(d)围压σ3c=200 kPa时的λ～εd关系曲线图

根据图4，在一定动应变下，随着干湿循环次数的增加，试样的阻尼比逐渐增大，表现试样在振动时应力波传输损耗能量增大，对于动荷载反应的滞后性有所增强。这主要是由于反复的干湿循环导致的土体内部裂隙发育，致使应力波在传输过程中损耗加大。同时，相同围压条件下，干湿循环次数多的试样起始段的斜率要略大于干湿循环次数少的试样，在较小的应变状态下便达到了接近最大阻尼比的状态。

2.6 不同干湿循环次数下的Edmax

根据图3以及式2，1/Ed～εd关系曲线呈线性关系，用最小二乘法求得参数A、B，从而推算出Edmax，得出不同条件下干湿循环次数～Edmax关系曲线，如图5所示。

图5 干湿循环次数和Edmax关系曲线图

根据图5可知，在0～5次干湿循环次数内，最大动弹模量Edmax随着干湿循环次数的增加而减小，且在第1、第2次干湿循环后有较大衰幅，第3次后衰幅减小，最大动弹模量Edmax趋于稳定。

2.7 不同干湿循环次数下的λmax

根据试验确定的干湿循环次数～最大阻尼比λmax关系曲线如图6所示。

图6 干湿循环次数和λmax关系曲线图

根据图6可知，在0～5次干湿循环次数内，最大阻尼比λmax随着干湿循环次数的增加而增大，且在第1、第2次干湿循环后有较大衰幅，第3次后衰幅减小，最大阻尼比λmax趋于稳定，但相对于围压、振动频率和固结比对最大阻尼比λmax的影响，干湿循环对试样最大阻尼比λmax的影响不大。

3 结语

通过重塑膨胀土和石灰处治膨胀土的物理力学试验以及动三轴试验结果分析，本文主要得出以下结论：

(1)膨胀土经6%的掺石灰量处治后土体的各项物理力学指标发生了较大变化，强度指标大大增加，塑性指数降幅明显，最大干密度降低，最优含水率升高，压缩特性增强，膨胀性基本被抑制，较好地改善了膨胀土的各项工程特性指标。

(2)根据等效线性模型(Hardin-Drnevich模型)提出的等效阻尼比公式，计算得到全应变范围内的阻尼比λ，根据试验结果确定最大阻尼比λmax；根据该模型提出的双曲线型动应力动应变关系，拟合计算得到最大动弹模量Edmax。

(3)通过动三轴试验得到干湿循环效应下石灰处治膨胀土动力特征，获得了0～5次干湿循环效应下的骨干曲线(σ～εd曲线)，随着干湿循环次数的增加，试样动应力水平不断衰减，其中第1、第2次干湿循环后动应力水平衰减幅度最大，第3次干湿循环后衰幅减小并逐渐趋于稳定，相同干湿循环次数条件下，随着围压增大，动应力水平衰减程度有所降低；随着干湿循环次数的增加，骨干曲线起始段的斜率有升高的趋势，即试样对动应力的敏感程度有所提升。骨干曲线出现明显的转角，说明试样具有明显的脆性性质。

(4)获得了0～5次干湿循环效应下的动弹模量与动应变关系曲线(Ed～εd曲线、1/Ed～εd曲线)，发现在干湿循环作用下，试样最大动弹模量不断衰减，其中第1、第2次干湿循环后最大动弹模量衰减幅度最大，第3次干湿循环后衰幅减小并逐渐趋于稳定，相同干湿循环次数条件下，随着围压增大，最大动弹模量衰减程度有所降低。

(5)获得了0～5次干湿循环效应下的阻尼比与动应变关系曲线(λ～εd曲线)，发现在干湿循环作用下，阻尼比随干湿循环次数增加而不断增大，其中第1、第2次干湿循环后阻尼比增幅较大，第3次干湿循环后增幅减小并趋于稳定，但相对于σ3c、Kc、f等因素，干湿循环效应对阻尼比的影响并不明显。

[1]曲永新.国内外膨胀土工程地质信息集成[R].中国科学院地质与地球物理研究所地质工程中心，2000.

[2]刘保东.石灰处治膨胀土路堤长期稳定性试验研究[D].南宁：广西大学，2008.

[3]杨明亮.石灰处治土膨胀土路基长期性能影响因素试验研究[D].武汉：中国科学院研究生院(武汉岩土力学研究所)，2010.

[4]Hardin B O，Drnevich V P.Shear Modulus and Damping in Soils[J].Journal of the Soil Mechanics & Foundations Division，2014，98：667-692.

[5]吴世明，周 健，杨 挺.土动力学理论与计算[M].北京：中国建筑出版社，2001.

[6]徐 毅.交通荷载对高速公路路基影响的试验研究[D].南京：河海大学，2006.

[7]中华人民共和国铁道部.新建时速300～350公里客运专线铁路设计暂行规定(铁建设[2007]47号)[S].北京，2007.

[8]杨广庆，管振祥.高速铁路路基改良填料的试验研究[J].岩土工程学报，2001(6)：682-685.