100 MN锻压机偏载承载能力分析

刘 豪，宋朝省，朱才朝，陈易明，杜雪松

(重庆大学 机械传动国家重点实验室，重庆 400044)

0 前言

锻压是金属加工的主要方法，是航空航天、车辆等行业不可或缺的加工工艺。近年来，随着我国高铁、航空航天等行业迅猛发展，锻压机制件需求量日益增加。由于锻压工艺要求 、安装条件限制等因素，在实际生产中，锻压机常出现偏心载荷等非标准工况，使锻压机部件可能出现强度破坏。

锻压机作为重型机械，其参数的设计计算及工作状态的模拟仿真对其安全可靠性尤为重要，国内外都对其强度分析、特性分析进行了一定的研究。刘跃峰等[1]采用六面体高阶单元建立了巨型模锻压机三维有限元模型，得到了其前六阶固有频率，并且分析了突然卸载时机架的瞬态响应，得到了机架卸载时的变形和应力分布。张勇[2]等采用有限元法建立了锻压机模型，得到了锻压机左右偏载工况下整机应力分布。马辉等[3]通过有限元仿真，确定了过盈装配时，过盈量与预紧力的关系。Tan J[5,6]等提出了一种锻压液压机柱体应力测试系统，对机架立柱进行应力测试。这些文献与研究成果均是围绕 “机架是承载偏心锻造载荷的主要元件”理论将锻造液压机抗偏载性能仅定义于对机架的受力分析[7]。李志波等将拉杆螺栓作为危险零件，分析了拉杆和拉杆强度之间的关系，提出了设计的可靠理论依据[8]。

本文针对100 MN模锻压机的偏载工况，通过理论计算和有限元建模，确定锻压机未出现强度破坏和开缝失稳的极限工况。

1 100 MN锻压机结构及理论最大偏心距

100 MN锻压机结构如图1所示，上横梁、下横梁、立柱通过拉杆螺栓预紧力连接，液压缸在液压油的作用下，通过传力部件推动活动横梁实现锻压工作。由于安装条件限制，锻压机主体与工作台存在斜置角度γ。

锻压机采用双球铰结构，使液压缸在偏载工况下，受力得到一定改善。双球铰结构在偏心载荷下的应力应变等还需要进行理论以及有限元分析，图2为双球铰结构示意图。

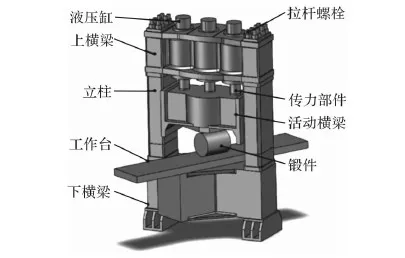
图1 100 MN锻压机结构图

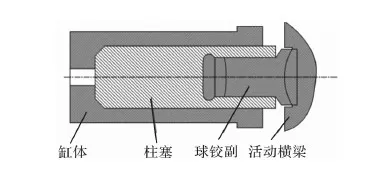
图2 双球铰结构示意图

锻压机工作缸采用球铰作为空间转动副，存在自锁特性[9,10]，锻压机在偏心载荷工况下，活动横梁将会处于自锁状态，而不会与立柱发生接触。此时，偏心锻造所形成的附加转矩将通过工作缸作用于锻压机的机架上横梁。当偏心量超过规定值之后，自锁状态将会被破坏，由于立柱与活动横梁之间存在间隙，活动横梁会发生转动，影响锻造质量。针对上述问题，对球铰自锁特性进行理论分析，确定锻压机最大偏心量。

根据球铰结构对单个球铰进行受力分析，受力如图3所示。

图3 球面任意点B的空间关系简图

设球面任意一点的压应力q按余弦分布，即球面任意一点的压力为

q=q0cosβ

(1)

式中，q0为球铰面最高点的压应力值；β为球铰面任意一点的圆心角。

则球铰上任意微面积上的正压力为

(2)

由Z向力平衡可得

FG=dFNcosβ

(3)

由式(3)得

(4)

式中，α为球面的最大张角，(°)；Rq为球面半径，mm。

由图3可知，

(5)

式中，

(6)

由图3所示，求解球面上任意一点的摩擦力对Y轴的摩擦力矩为

dMf=μdFNcosβ·l

=μq0Rql2cosβsinβdθdβ

(7)

式中，μ为球面静摩擦系数。

球面绕Y轴的静摩擦力矩为

Mf=dMf

(8)

列力矩平衡方程∑Y=0，得到

Mf-rFG=0

(9)

式中，r为球铰摩擦圆半径，mm。

100 MN锻压机采用球墨铸铁和45钢作为球铰副材料，由机械设计手册查表得摩擦因数为0.2～0.3，取较大安全系数，因此采用0.2作为摩擦因数。

由此可得

(10)

当锻压机模具与工件接触时，锻压机工作缸开始加载，球铰摩擦阻力矩将随着载荷的增加而增加。如果偏心载荷形成的转矩大于球铰阻力矩，球铰转动，活动横梁将发生摆动。为了保证锻造精度，在锻造过程中，球铰应处于自锁状态，才能满足偏心锻造的基本条件。

该型锻压机三个液压缸型号相同，由同一油泵供油，因此液压缸提供的压力是相同的，记为F1G。锻造偏心距小于球铰自锁偏心距时活动横梁在XZ平面的受力情况如图 4所示。

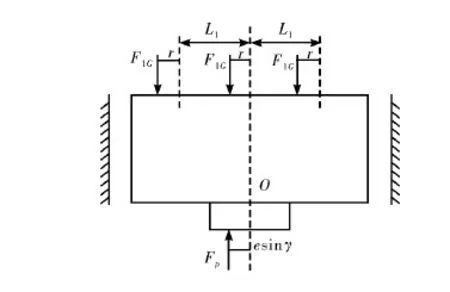
图4 活动横梁未摆动时XZ平面受力简图

取活动横梁和上砧为整体，力矩平衡方程为

esinβFP+(L1-r)F1G=rF1G+(L1r)F1G

(11)

力平衡方程：

FP=3F1G

(12)

式中，e为压机的锻造偏心距，mm；γ为工作台的斜置角度，°；F1G为液压缸的推力；R为液压缸的球铰自锁半径；L1为液压缸中心距。

则有锻压机自锁载荷偏心距e为

(13)

2 基于有限元的锻压机承载能力分析

2.1 锻压机强度计算模型

根据锻压机的安装情况，锻压机下半部接地，为提高计算效率，将锻压机下半部假设为刚体，只对锻压机上半部进行分析。

在ABAQUS中建立锻压机上半部分有限元模型，进行有限元分析，如图5所示。

图5 ABAQUS有限元模型

锻压机安装时，需要进行螺栓预紧，共16个螺栓拉杆。在螺栓中切取一个截面，施加ABAQUS中的螺栓力(bolt load)。模型下部施加全约束。下横梁底部模具与锻件接触面，施加偏心载荷，有限元模型边界条件如图6所示。载荷工况选取如表1所示。

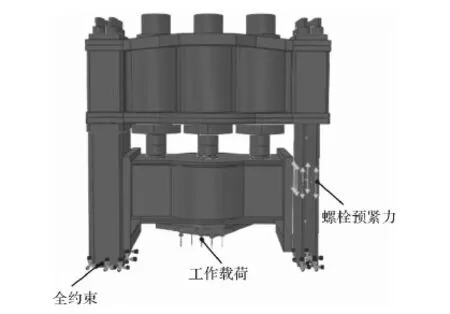
图6 有限元模型边界条件

工况12345678载荷/MN100100908070605040

模型设置无摩擦接触包含：立柱与上横梁、螺母与垫片、连接体与上球面、下球面，其余均为绑定。

2.2 承载能力分析

由于100 MN为载荷极限工况、40 MN为接近理论载荷偏心量的极限，因此本文取工况1、工况2和工况8进行详细结果对比。

横梁与立柱之间的开缝判定是锻压机是否正常工作的一个重要指标，根据文献[4]，取未开缝标准：上横梁与立柱实际接触面积与总面积比值在0.5以上。

如图7所示，接触面积与总面积比值均大于0.5，由于边缘接触，表面压力最大点均在锻压机立柱外侧。工况1表面压力分布较为对称，偏载之后，压力分布也不再对称，与载荷偏载方向相同。工况2表面压力最大值为47.9 MPa。工况8表面压力最大值增大到58.2 MPa。

图7 立柱表面压力对比

如图8所示，工况1最大应力发生在螺栓拉杆处，最大应力为343.7 MPa，传力部件应力分布较为均匀。工况2和工况8最大应力发生在传力部件载荷偏心方向倒角处，最大应力分别为482.8 MPa、472 MPa。

图8 整机应力云图对比

如图9所示，工况1连接体应力分布较为均匀，编号1、编号3外侧应力较大，最大应力为209 MPa。工况2连接体在载荷偏心另一侧应力几乎为0，工况8连接体在载荷偏心另一侧有较小应力，两种工况最大应力均发生在连接体载荷偏心方向倒角处，最大应力分别为482.8 MPa和475 MPa，接近材料屈服点。

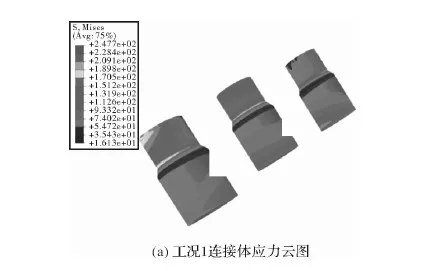
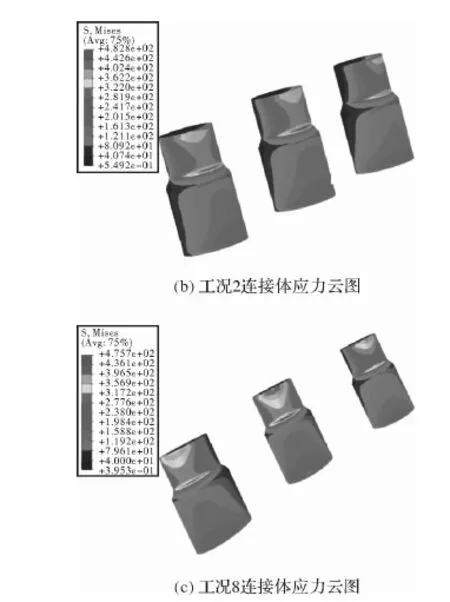
图9 连接体应力云图对比

如图10所示，在工况1中，球面垫应力分布对称，载荷集中在中间，最大应力为167 MPa。工况2中球面垫只有一半球面承受载荷，最大应力发生在球面垫侧面，最大应力为255 MPa。工况8只有一半球面承受载荷，最大应力为345 MPa。

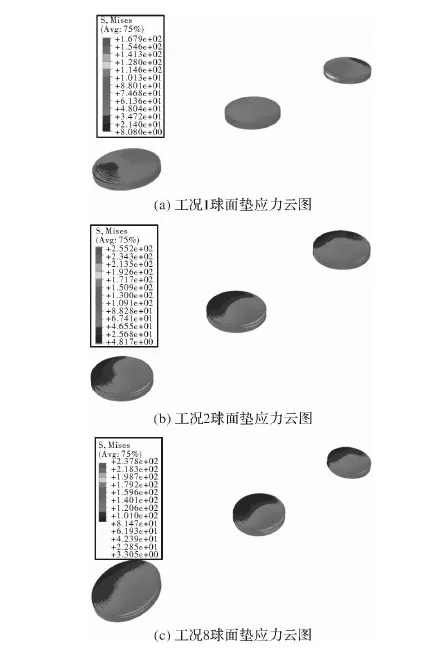
图10 球面垫应力云图

由仿真结果可知，各种偏载工况下，均是连接体最先接近材料屈服极限，由此可得各个载荷下的极限偏载量，如图11所示。

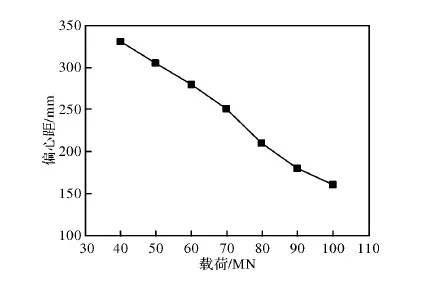
图11 不同载荷对应的极限偏载量

如图12所示，在各个偏载工况下，锻压机连接体安全系数最先接近1，此时上横梁、拉杆螺栓、球面垫、立柱等关键部件安全系数均大于1.4，未达到材料屈服极限。

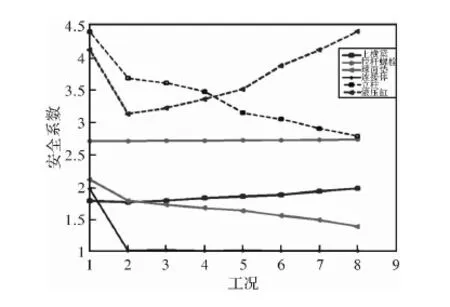
图12 不同工况下各部件安全系数

3 结论

本文以100 MN锻压机为研究对象，建立锻压机上半部有限元接触分析模型，以确定锻压机各个偏心载荷工况下极限偏心距，得到主要结论如下：

(1) 当锻压工况未发生偏载时，螺栓拉杆是主要的承力部件，当锻压工况发生偏载时，液压缸球铰是承担偏心载荷的主要承力部件；

(2) 在保证强度、锻造精度的前提下，锻压机最大偏心量为330 mm，对应载荷为40 MN，当载荷工况为100 MN时，最大偏心量为160 mm；

(3) 各种偏载工况中，锻压机最容易发生强度破坏的部件均为液压缸连接体，此时其他部件均未达到强度极限。

[1] 刘跃峰, 冯翠云, 邹春来. 巨型模锻压机机架有限元动态分析[J]. 桂林理工大学学报, 2011, 31(02):292-295.

[2] 张勇, 艾志久, 武艳,等. 锻压机左右偏载工况下整机结构分析及优化[J]. 热加工工艺, 2013(23):156-159.

[3] 马辉, 能海强, 宋溶泽,等. 两种工况下锻压组合机架的接触特性分析[J]. 东北大学学报(自然科学版), 2013, 34(09) :1300-1304.

[4] Chen H, Tan JP, Gong JL, et al. Research on Mathematic Model and Measuring Method of Moving Beam Attitude in Large Forging Hydraulic Press[J]. Applied Mechanics & Materials, 2012, 128-129:1213-1216.

[5] Tan J, Chen H, Gong J. Influence of Moving Beam Horizontal Offset on Additional Column Stress in Large Forging Hydraulic Press[J]. Journal of Computational & Theoretical Nanoscience, 2012, 6(01):280-284.

[6] Hui C, Tan J, Gong J, et al. New Stress Testing System for Columns in Large Forging Hydraulic Press[J]. Journal of Vibration Measurement & Diagnosis, 2012, 32(03):375-471.

[7] Zhang YG, Yan H, Liu Z Q, et al. Modal Analysis on the Inclined Double-Column and Pre-Stress Combined Frame Structure of the 80MN Rapid Forging Hydraulic Press[J]. Advanced Materials Research, 2011, 317-319:484-488.

[8] Zhi-Bo LI, Dong G J, Shu-Liang W U, et al. Finite element analysis of 12.5 MN high speed forging hydraulic press frame[J]. Forging & Stamping Technology, 2008, 32(06):1403-1411.

[9] 刘艳妍, 杨晋. 双柱式锻造液压机工作缸球铰力学分析[J]. 机械科学与技术, 2014, 33(06):789-791.

[10] 刘艳妍, 杨晋, 马学鹏,等. 上推式快锻液压机活动横梁转动自锁条件研究[J]. 机械工程学报, 2014, 50(08):66-72.