磁极结构对永磁同步伺服电机转矩脉动的影响

于慎波，李 野，钟双双

(沈阳工业大学 机械工程学院，沈阳 100870)

0 前言

随着我国对稀土能源的有效利用，电机材料及相关加工工艺的完善，永磁电机得到了广泛的应用。高性能的交流永磁伺服电动机具有功率因数高、效率高、动态响应速度快、转动惯量小、低速平稳性好等诸多优点，广泛用于装备制造业( 机床、机器人等) 、医疗设备、家用电器等场合[1]。数控机床作为现代生产加工的主力军更是广泛采用永磁伺服电机。其独特新颖的结构设计，使电动机的材料利用率提高，体积小，功率高。传统永磁同步电机磁极采用瓦片式结构，其永磁体结构产生的气隙磁密波形近似方波而存在。不同转子结构的气隙磁场中谐波含量有较大差异，谐波含量越大，电机的不稳定性越差，同时谐波的存在还会产生附加的转矩脉动，导致电机产生噪声和振动[2]。转矩脉动作为衡量永磁电机质量好坏的标准之一，得到了越来越多学者的关注。文献[3]通过改进的磁化建模方法，解决不同厚度的磁体数学表达式的解析解，实现电磁转矩的准确计算和转矩脉动的削弱。文献[4]基于齿槽转矩最小化对永磁极进行结构设计，建立了半闭口槽的磁场分布二维解析解。文献[5]提出了半闭口槽解析子域模型，该模型准确地反映了电枢反应磁场和槽间相互影响，为综合降低转矩脉动提供理论支撑。文献[6]以内置式永磁同步电机为研究对象，提出“M”型新转子结构，以优化气隙磁密，减少谐波分量。文献[7]采用解析法和有限元法相结合的方式，阐述闭口槽降低齿槽转矩的有效性。文献[8]分析解释了拼接式闭口槽的合理性，并对不同拼接方式进行对比分析。本文将以拼接式闭口槽永磁同步电机作为分析对象，提出三段弧磁结构，对比传统瓦片式磁极，建立不同结构的永磁体有限元模型。通过改变优化磁极外形参数，改变电机气隙磁场分布规律，进而实现对电机气隙磁场的优化，使绕组的反电动势波形尽可能接近理想波形，以此来削弱电机的转矩脉动。

1 磁极的弧形理论

1.1 基本磁极理论

探究永磁同步电机的转矩波动，可以从两方面考虑，第一，考虑定子齿槽对气隙磁场的影响，即尽可能的降低电机的齿槽转矩。第二，考虑电机永磁体产生的磁场对气隙磁场的影响。当忽略电机定子齿槽对气隙磁场分布的影响时，气隙磁场的磁密曲线呈矩形分布。将永磁体沿周向展开理想化得到永磁体外表面形函数。图1为传统瓦片式磁极结构。

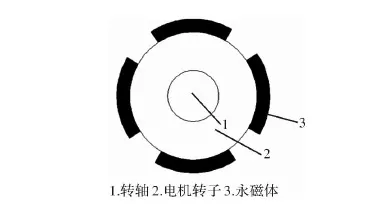
图1 传统瓦片式磁极

对应的函数如下[9]：

(1)

其中A(l)为圆弧形状函数，当形状函数为等半径圆弧时，A(l)为定值。将式(1)进行傅里叶级数展开。傅里叶级数展开形式为

(2)

式中，

(3)

(4)

an和bn为傅里叶系数。由于式(1)关于原点对称，为奇函数，所以其傅里叶级数展开式只含有正弦项。将式(1)做谐波分析，然后进行奇延拓，傅里叶级数展开可得

(5)

(6)

其中k=1,2,3,…,因此式(1)可得

(7)

由分析可得，电机的气隙磁密不含3的倍数次谐波和偶数次谐波。通过采用永磁体周向相对位置固定的分布方式，能够削弱气隙磁密的偶次谐波分量，为后续的理论分析提供支撑。

1.2 三段弧磁极理论

由数学分析表明，当永磁体外表面形状越逼近正弦，其谐波含量越少，振动浮动和转矩波动也越小。因此提出一种合理化转子结构：永磁体外表面将由三段圆弧代替，通过对圆弧的形比修正系数和中心截面系数等重要参数进行修正使永磁体外形更逼近正弦。三段弧磁极结构如图2所示，其中1为转轴，2为电机转子，3为三段弧磁极。相应的函数可简化为

(8)

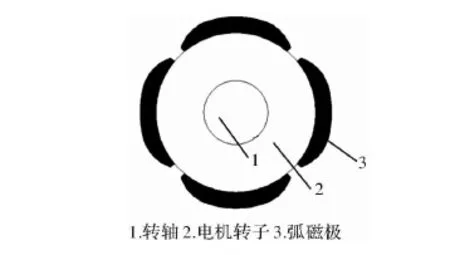
图2 三段弧式磁极

其中A(l)分别为中间段圆弧形状函数，B(l)为两侧段圆弧形状函数。为了获得良好的性能，将两侧圆弧认为关于中心圆弧对称分布。由于F(x)为奇函数，故谐波分析奇延拓后可得

B(l)(cosnb1+cosna1-cosnb1-cosna2)]

(9)

对式(9)做进一步分析，假设a1=π-l1，a2=π-l2，b1=l2，b2=l1，且l1=5π/2-l2，A(l)=βB(l)，其中β为形比修正系数，将参数带入式(9)，则

其中k=1,2,3,…。通过对式(9)的傅里叶级数展开如下

(10)

(11)

结合式(11)再将β、l1、l2、l分别代入式(7)和式(10)中，可得

(12)

当且仅当n=12的倍数时，均值不等式两侧相等。在假设条件下，磁极采用三段弧形设计的基波幅值分量要小于传统瓦片式磁极。但这种条件下却能有效的减少气隙磁场中的非零谐波分量，使电流波形、反电动势波形更接近正弦，因此三段弧磁极的构想是可行的。

2 电机的有限元分析

2.1 电机结构和参数设计

根据理论参数对三段弧式磁极形函数进行结构参数化拟合。通过MATLAB等数据处理软件对数据点进行曲线拟合，得到三段弧式磁极形状参数。根据此条件下拟合得到的形状参数建立有限元仿真模型。拟合得到三段弧参数如表1所示。

表1 三段弧拟合参数

为了降低定子齿槽对气隙磁场的影响，有限元模型采用表贴式闭口槽永磁同步伺服电机为基础模型，其定子采用定子冲片拼接而成，考虑到模型的结构和仿真精度，会对其适当简化。具体模型如图3所示。

永磁体材料采用钕铁硼，极对数为4，定子冲片数为12，定子节距为1，每个线圈312匝，电机结构参数如表2所示。

图3 基础模型的电机结构

参数参数值定子外径/mm122定子内径/mm80转子最大外径/mm79.2转子最小外径/mm72定子长度/mm48轴外径/mm37有效气隙长度/mm0.8输出功率/kW0.85永磁体材料钕铁硼

2.2 永磁体截面中心系数

为了最大限度得到弧形最优解，有效控制永磁体外形函数，假设中心弧度角两侧对应的弧度角相等，且两侧弧长半径均相等。即将永磁体外表面分成三段，中间部分由中心弧度角决定，其圆弧形状函数为A(l)，其余两侧相互对称，采用拟合得到的半径和圆心，其圆弧形状函数为B(l)，为了体现圆弧形状函数A(l)，现定义永磁体截面中心系数为:

(13)

式中，角α为电机转子永磁体的极距；角θ为永磁体中心弧度角。当Kc等于0时磁极为最初的瓦片式结构。

通过修改永磁体截面中心系数，定量研究永磁体不同中心系数下的转矩脉动和额定转矩变化趋势，确定有效的磁极外形结构，降低转矩脉动及反电动势中的谐波。

如图4所示，其中R1为定子内径，R2为永磁体最大半径，R3为永磁体与转子接触面的半径。R4为转子内径。其中b为永磁体径向最大厚度。充磁方式采用径向充磁。运用ansoft仿真出基础模型的磁场分布如图5所示。

图4 永磁体截面参数图

图5 基础模型的磁力线分布图

3 电机仿真分析

应用ansoft对不同中心系数下的气隙形状进行有限元分析，如图6所示。

图6 不同中心系数下的转矩脉动和额定转矩

由图6可知，永磁体表面形状是影响转矩脉动的重要因素，因为永磁体表面形状对气隙磁导的影响，会严重影响气隙内的磁场分布，从而影响转矩脉动的变化。图6中的曲线1为不同中心系数下转矩脉动的趋势，曲线2为不同中心系数下的额定转矩的变化趋势。综合图6中的双曲线可以确定，三段弧结构能够有效降低电机的转矩波动。当Kc等于1/5或Kc等于1/2的时候，转矩脉动最小同时额定转矩降低率较低。从经济角度考虑，当Kc等于1/2的时候，永磁体用量大。因此当Kc等于1/5时，为最优值。

考虑到充磁方式也会影响Kc，因此再采用径向充磁对现有模型进行仿真。仿真结果如图7所示。

由图7可知，本样机在径向充磁下的转矩脉动分布情况与平行充磁的转矩脉动分布情况类似。通过图6和图7中转矩脉动曲线对比可以，径向充磁下的转矩脉动值普遍大于平行充磁下的转矩脉动值。但当Kc为0和1/3时，两种情况下的转矩脉动相近。通过图6和图7中的额定转矩曲线对比可知，径向充磁与平行充磁对额定转矩削弱程度相近，径向充磁对额定转矩的削弱程度更大一些。因此，对于本样机而言，采用平行充磁更好。

图7 径向充磁不同中心系数下的额定转矩和转矩脉动

取Kc等于1/5时的电机模型仿真结果得到径向气隙磁密如图8所示。输出转矩如图9所示。同时将三段弧磁极下的单相反电动势与瓦片式磁极下的单相反电动势做对比，得出三段弧磁极能够有效的改善反电动势波形，减少谐波分量。如图10、图11所示。

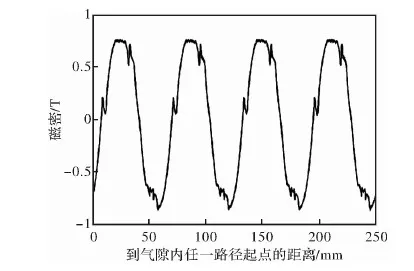
图8 三段弧磁极径向磁密

图9 三段弧磁极输出转矩

图10 瓦片式磁极单相反电动势

图11 三段弧磁极单相反电动势

4 结论

本文主要研究了削弱高精密数控机床用永磁同步伺服电机转矩脉动的方法，通过对8极12槽拼装式闭口槽永磁同步伺服电机进行有限元分析发现：三段弧磁极比传统瓦片式磁极拥有更优良的特性。改善永磁体外表面的形状能够影响气隙分布，进而削弱转矩脉动。通过改变永磁体截面中心系数，仿真出不同情况下的转矩脉动和额定转矩的变化规律。综合仿真分析结果：采用三段弧式磁极结构，Kc等于1/5并采用平行充磁时为最优参数，此时转矩脉动为2.73%。研究发现，合理改变永磁体外表面的结构和充磁方式能够有效的降低转矩脉动。

[1] 唐任远，赵清，周挺．稀土永磁电机正进人大发展的新时期[J]．沈阳工业大学学报，2011，33(01)：1-8.

[2] 方程，许海平，薛劭申，等．直驱型多相永磁同步电机定子磁动势与气隙磁密特性分析[J]．中国电机工程学报，2013，33(24)：106-113．

[3] S.-M. Jang, H.-I. Park, J.-Y. Choi, K.-J. Ko, and S.-H. Lee.Magnet pole shape design of permanent magnet machine for minimization of torque ripple based on electromagnetic field theory[J].IEEE Trans.Magn.,2011,47(10) : 3586-3589

[4] B. L. Chikouche, K. Boughrara, and R. Ibtiouen.Cogging torque minimization of surface-mounted permanent magnet synchronous machines using hybrid magnet shapes[J].Progress Electromagn. Res. B, 2015,64: 49-61.

[5] T.Lubin, S. Mezani,and A. Rezzoug,2-d exact analytical model for surface-mounted permanent-magnetmotorswith semi-closed slots[J].IEEE Trans. Magn.,2011,45(02) : 479-492.

[6] 张炳义，张霄霆，姜珊珊.电动汽车永磁同步驱动电机优化波形质量方法[J]．沈阳工业大学学报，2017，39(05)：481-485.

[7] 周洲,杨立.降低齿槽转矩的闭口槽结构永磁无刷电机分析及设计方法[J].微电机，2014,47(05)：6-8.

[8] 袁健,沈建新, 史涔溦等.定子拼装式永磁同步电机齿槽转矩研究[J].微电机,2015,48(03)：1-4.

[9] 王海星,李志义,封海潮.表贴式永磁电机阶梯形永磁体设计及特性分析[J].合肥工业大学学报:自然科学版,2015(09)：1197-1201.