越野汽车驾驶室底板对爆炸冲击的响应研究

石秉良 王显会 盘朝奉 张明 张元正

（1.江苏大学，镇江 212013；2.陆军汽车试验场，南京 210028；3.南京理工大学，南京 210094）

1 前言

越野汽车由于具备优越的机动能力，在各国军队中得以广泛应用，随着战争形态的发展变化，其受到来自底部的爆炸袭击威胁日显突出。地雷等简易爆炸装置在驾驶室底部爆炸引起的损伤，是非对称战争中车辆及其乘员受到的主要损伤模式之一[1]。车辆应对爆炸冲击的能力越来越受到人们重视，驾驶室底板是车辆受到爆炸冲击时对乘员形成保护的第一道防线，对爆炸冲击波作用下越野汽车驾驶室底板结构的响应进行分析与研究是开展车辆底部防护能力研究的基础[2]。

对爆炸冲击作用下车辆驾驶室底板结构的塑性动力响应进行仿真分析，能获得较好的虚拟试验结果，可为车辆驾驶室底部防护结构设计提供参考依据[3]。1953年，Bruce等[4]模拟了一维气相不稳定径向和线形流，数值仿真技术诞生；J.O.Hallquist博士[5]在1976年主持并完成了LS-DYNA软件的开发，较好地解决了非弹性材料结构在高速碰撞和爆炸冲击载荷下的塑性大变形动力学响应的三维求解问题。K.Willianms等[6]通过数字仿真对预埋的7.5 kg C-4地雷替代品在底部加装防护组件的M113 MTVL底部爆炸时的作用效果进行了系统的仿真分析研究，利用LS-DYNA软件将车体分为9部分划分有限元单元格，并用Westine经验公式计算节点速度。Craig Barker等[7]同样利用Westine爆炸冲击经验公式对车辆底部受到爆炸冲击时车辆底板的速度响应进行了分析，为进一步研究直接与底板接触的乘员下肢运动提供了理论依据。

此方面的研究工作，近年来国内才得以重视，采用任意拉格朗日-欧拉（Arbitary Lagrange Euler，ALE）算法，利用LS-DYNA软件对爆炸冲击作用下典型越野汽车驾驶室底板结构响应的影响因素和不同当量炸药爆炸作用下的响应进行分析研究，可对车辆底部结构的防护能力进行预测和优化分析。

2 仿真计算理论模型

2.1 简化系统几何模型

车辆底板结构通常较为复杂，本文将车辆底部板结构简化为四边约束的标准靶板，地雷等简易爆炸装置的爆炸产物对车辆底部板壳结构的作用简化为爆炸冲击波对靶板的作用，作用系统简化为炸药-靶板系统几何模型[8]，如图1所示。

图1 炸药-靶板系统几何模型

炸药-靶板系统几何模型中，靶板为边长500 mm、厚2 mm的方形结构，靶板材料选择Q235号钢，密度ρ=7.8 g/cm3，弹性模量E=210 GPa，切线模量Et=466 MPa，泊松比v=0.30，屈服应力σs=235 MPa；炸药为裸装圆柱形TNT药柱，药量为700 g，长径比为1∶1，采用中心引爆的方式。靶板采用四边约束的方式固定在距炸药中心点470 mm的位置，中心正对炸药。

炸药-靶板系统几何模型中，炸药爆轰采用高能燃烧模型，产物状态方程采用JWL[9-10]方程：

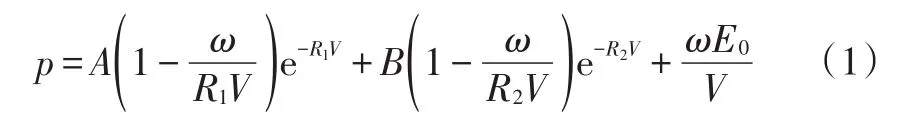
式中，A、B、R1、R2、ω为材料参数；p为高能炸药材料内压力；V为相对体积；E0为初始比内能。炸药的材料参数和状态方程参数如表1所示。

2.2 ALE算法炸药-靶板系统基本模型

在仿真计算中，利用法向约束的方法在模型的对称面中设置对称约束，建立1/4有限元模型，如图2所示。ALE算法需要模拟爆炸冲击波，计算时将流固耦合方法用于冲击波对靶板作用的响应[11-14]，为了提高计算效率，模型中仅建了局部的空气域，并在空气网格表面设置无反射边界条件以模拟无限空气域。炸药物质与空气介质为欧拉单元，靶板为拉格朗日单元，且炸药与空气网格的节点融合，空气单元覆盖靶板，炸药的初始引爆点设在炸药中心位置处。如图2所示，炸药-靶板爆炸仿真有限元模型网格单元数为309 796，节点数为317 542。

表1 炸药材料参数及状态方程参数

图2 ALE算法炸药-靶板系统1/4基本模型

2.3 地雷-空气-车辆系统仿真模型

为较准确地分析爆炸冲击作用下某型越野汽车驾驶室底板的响应，应在整车环境中进行研究，本文建立了地雷-空气-车辆系统仿真模型，如图3所示。

图3 地雷-空气-车辆系统仿真模型

建模时将整车三维建模软件中的CAD模型导入有限元前处理软件Hypermesh中。车身结构件模型中包含了大量倒角与内、外饰安装孔，由于显式计算中网格尺寸直接影响了计算的时间步长，为了避免一些不重要的细微几何信息造成网格划分困难，导致计算无法收敛，在进行网格划分之前，对CAD模型进行一定的简化与几何清理，清理后驾驶室底板模型如图4所示。

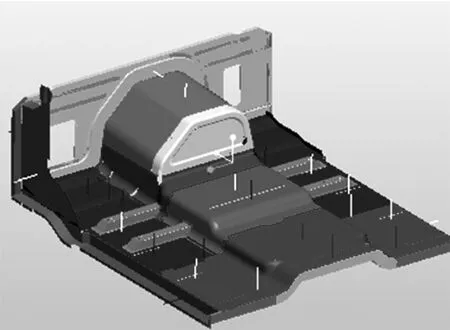
图4 某型越野汽车驾驶室底板CAD模型

3 驾驶室底板响应研究

炸药在车辆底部爆炸时，驾驶室底板是车辆底部直接对乘员形成保护的关键部件，乘员座椅通常直接安装在底板上，脚部也通常直接放置在底板上。爆炸冲击的巨大能量通过驾驶室底板、座椅等间接作用于车内乘员，从而造成伤害。不同炸药爆炸后，驾驶室底板的冯米斯应力（von Mises Stress）云图和位移云图如图5所示。

图5 驾驶室底板仿真云图

从图5中可以看出，在规格为326 g地雷替代品的爆炸冲击波作用下，驾驶室底板已经出现了较多的塑性变形区域。从应力云图可知：驾驶室底板在结构的边缘、接合处、加强筋布置处均出现了超过450 MPa的应力区域；随着当量的增加，驾驶室底板的变形增加明显，在规格为755 g地雷替代品的爆炸冲击波作用下，驾驶室底部中心变形最大，底板在爆炸冲击波作用下最大变形挠度接近90 mm。但驾驶室没有出现结构贯穿的损伤。

为进一步分析爆炸冲击对驾驶室底板的影响，在驾驶室底板上设置了5个测量点，如图6所示。仿真过程中采集位置1、2、3、5的加速度时间历程和应力时间历程进行分析。755 g炸药爆炸时反应较为剧烈的位置2的加速度时间历程见图7，各测量点应力时间历程见图8。

图6 驾驶室底板仿真测量点布置

图7 位置2加速度时间历程

图8 驾驶室底板关键位置应力时间历程

通过对驾驶室底板的4个测量点的加速度和应力时间历程进行分析可知，地雷爆炸冲击时驾驶室底板中心（位置1）具有最大的应力峰值，此处容易产生结构变形；驾驶室中间后端（位置2）处，出现了较大的加速度响应，且该位置在爆炸冲击作用下加速度具有明显跃升趋势，此处容易给车内乘员相关部位直接或间接造成较大的冲击。

4 爆炸冲击对驾驶室底板影响分析

根据初步分析，对车辆驾驶室底板受到爆炸冲击后的响应影响较大的因素主要有爆炸物当量、驾驶室底板厚度和底板材料。本文主要从不同炸药当量、不同材料厚度方面分析爆炸冲击对驾驶室底板影响，同时对驾驶室底板响应特性对不同材料特性参数的灵敏度进行分析。在驾驶室底板模型上选取A（480 948）、B（483 538）、C（487 878）、D（498 628）等4个测量点，如图9所示。仿真分析中，重点分析驾驶室底板整体应力情况和不同测点的变形情况。

4.1 爆炸物当量

为了分析爆炸物当量对驾驶室底板响应的影响，研究中选择了材料厚度为5 mm的钢板，分别以552 g、998 g、1 500 g、2 029 g等4种不同当量的炸药进行仿真。不同当量炸药爆炸时驾驶室底板应力情况如图10所示；4个测量点变形情况如图11所示。

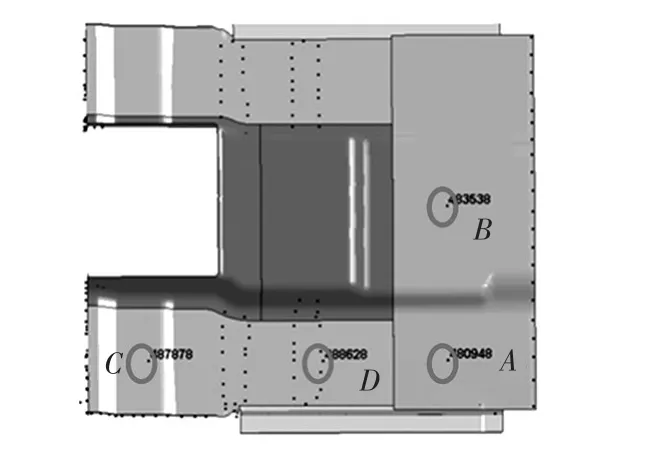
图9 驾驶室变形测量点示意

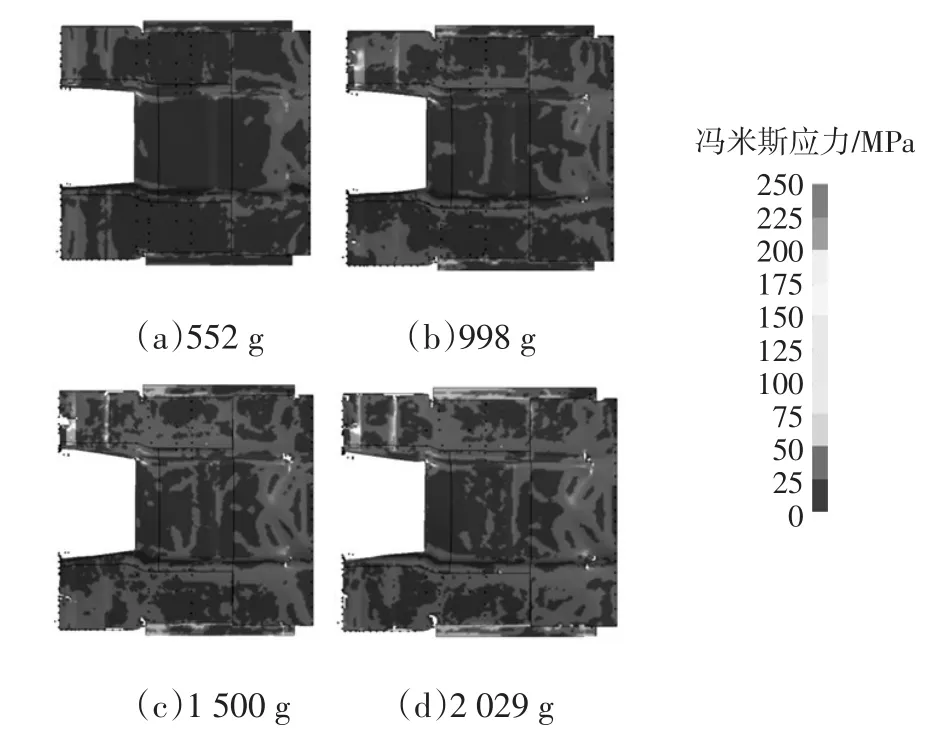
图10 不同炸药当量情况下驾驶室底板冯米斯应力云图

从图10可以看出，当炸药当量超过998 g时，驾驶室底板边缘处已经出现了局部撕裂，驾驶室中后部也出现了贯穿性损伤，这说明采用5 mm钢板的该型驾驶室底板，在不采取任何底部防护措施的条件下，将无法抵御超过998 g当量炸药的爆炸冲击。

通过分析4种不同炸药当量条件下4个测量点的位移变化情况进行比较可知：不同当量炸药爆炸时，驾驶室底板关键测量点的变形时间历程曲线的形态相似，随着地雷当量的增加，测量点位移幅度逐渐变大，例如测量点A在不同炸药条件下均是在9 ms时刻达到最大变形。

对4个测量点在不同炸药条件下的变形最大幅值进行统计分析，结果如图12所示。在552 g、998 g、1 500 g当量炸药的爆炸作用下，测量点变形幅值变化趋势基本相同（斜率近似）。但炸药当量从1 500 g增加到2 029 g时，测量点的位移幅值出现了两种情况：测量点C的位移变化斜率突然增加，说明该点的变形幅值变化对炸药当量较为敏感，在车辆底部防爆炸冲击结构优化设计中，可考虑对此处的结构进行适当加强；测量点A和B变形变化斜率随着炸药当量的增加而减小，说明测量点A和B的位移幅值变化对炸药当量变化敏感度较小，在车辆底部防爆炸冲击结构优化设计中，可考虑适当减小此处材料厚度。

图12 地雷当量与不同测量点的位移对比

4.2 材料厚度

为了研究驾驶室底板材料厚度对其底部防护能力的影响，以998 g当量炸药爆炸冲击作为仿真输入，分析材料厚度分别为1 mm、3 mm、5 mm、7 mm时驾驶室底板的应力与变形情况。4种不同厚度时驾驶室底板的冯米斯应力云图如图13所示。从仿真分析结果可知，随着底板材料厚度不断增加，底板产生的最大应力不断减小，但图中这一现象并不明显，这是因为在4种不同厚度的爆炸分析中底板边缘的约束部分均出现了较大的应力集中，而驾驶室底板中心位置在998 g当量炸药的爆炸冲击下均没有出现贯穿损伤，也没有出现超过强度极限的位置。

图13 不同厚度底板冯米斯应力云图

材料厚度分别为1 mm、3 mm、7 mm时驾驶室底板变形测量点的位移时间历程曲线如图14所示。4个测量点在998 g当量炸药的爆炸冲击作用下，变形结果有较大区别。其中，测量点B由于更靠近爆炸中心，变形最大，随着底板材料厚度不断增加，测量点的变形减小，节点位移历程曲线变化趋势符合预期。

将不同材料厚度情况下4个测量点的位移峰值进行统计，如图15所示，对于测量点B、C、D，在1 mm与3 mm的不同料厚情况下，其位移变化衰减明显。其中，测量点C的位移变化对料厚最为敏感，但不同材料厚度条件下的测量点A处的位移变化不明显，这说明在后期优化设计中，在测量点B、C、D对应的位置应适当增加材料厚度，才能有效提升驾驶室底部防护能力，而对于测量点A对应的位置可适当考虑相应的轻量化措施。

4.3 材料特性参数

材料特性参数影响着材料的各项性能，同样对材料的抗爆炸冲击能力有着较大的影响，但各种参数影响程度不同。研究材料不同特性参数变化对驾驶室底板对炸药爆炸冲击波响应的影响时，选择当量为998 g的炸药，将驾驶室底板材料的弹性模量E、切线模量Et、泊松比μ及屈服强度σ作为设计变量，以驾驶室底板的变形响应作为目标函数，进行参数灵敏度分析。驾驶室底板材料参数初始值及变化范围如表2所示。

由于整车爆炸仿真试验计算量大、耗时较长，仿真试验设计时应尽量缩减试验中水平值，从而减少试验设计中爆炸仿真的计算成本。本文使用多变量二水平筛选的Plackett-Burman试验建立参数筛选样本空间，各变量的水平差值不能过大（高水平为低水平的1.5倍以内），不考虑因子之间的交互效应，通过Plackett-Burman采样结合方差分析（Analysis of Variance，ANOVA）能高效地对多因子空间的结构变量进行一阶灵敏度分析，从而有效地判断各个变量对响应函数的贡献，缩减变量的样本空间[15]。对车辆驾驶室底板的4个特性参数进行变形响应的全局灵敏度分析，结果如图16所示。由图16可知，4个变量中泊松比μ对响应目标函数结果影响最大，其次是弹性模量E。

5 结束语

采用任意拉格朗日-欧拉算法，对某型车辆驾驶室底板抗爆炸冲击能力进行了仿真分析与研究，对炸药当量、底板材料厚度对驾驶室底板抗爆炸冲击能力影响规律进行了研究，分析了材料特性参数对材料变形目标函数的灵敏度，主要结论有：

a.随着炸药当量的增加和材料厚度的减小，该车辆驾驶室底板的破坏程度均会加大，当炸药当量为988 g时，该车辆驾驶室底板即便采用5 mm的钢板也会被击穿；

b.在材料厚度不变的情况下，测量点A、B的位移幅值变化对炸药当量变化敏感度较小，在车辆底部防爆炸冲击结构优化设计中，可考虑适当减小此处材料厚度，同时应适当增加C、D点处厚度。

c.在炸药当量不变的情况下，测量点B、C、D对应的位置应适当增加材料厚度，才能有效提升驾驶室底部防护能力，而对于测量点A对应的位置可适当考虑相应的轻量化措施。

d.弹性模量E、切线模量Et、泊松比μ及屈服强度σ等4个材料特性参数中，E、μ对变形响应的目标函数灵敏度较高，车辆驾驶室底板设计时应合理选择材料。

[1]Grujicic M,Bell W C.A Computational Analysis of Survivability ofa Pick-up Truck Subjected to Mine Detonation Loads[J].Multidiscipline Modeling in Materials&Structures,2011,7(4):386-423.

[2]石秉良,王显会,张云,等.军用车辆底部防护发展与研究综述[J].兵工学报,2016,37（10）：1902-1914.

[3]Müller M,Dierkes U,Hampel J.Blast Protection in Military Land Vehicle Programmes:Approach,Methodology and Testing[C]//Structures under Shock and Impact.2012:247-257.

[4]Bruce G H,Peaceman D W,Rachford H H,et al.Calculation of Unsteady-State Gas Flow Through Porous Media[J].Journal of Petroleum Technology,1953,5(3):79-92.

[5]胡远志,曾必强,谢书港.基于LS-DYNA和HyperWorks的汽车安全仿真分析[M].北京：清华大学出版社,2011：11-17.

[6]Willianms K,Poon K.A Numerical Analysis of the Effect of Surrogate Anti-tank Mine Blasts on the M133，DREV TM-2000-007[R].Canada:National Defense,2004:1-19.

[7]Barker C,Howle D.Predicting Floor Velocity of a Vehicle Subjected to an Underbody Blast Event[C]//Craig B,et al.Eightyth Shock & Vibration Symposium,Shock and Vibration Information AnalysisCenter(SAVIAC),San Diego,USA,2009:719-729.

[8]石秉良,周孔亢,张云,等.基于SPH算法的驾驶室底部结构对爆炸冲击波响应数值仿真[J].机械工程学报,2016,52（16）：132-139.

[9]陈娟.水下爆炸冲击载荷的SPH算法研究[D].哈尔滨：哈尔滨工程大学,2010.

[10]徐定海,王善,杨世全.板壳结构接触爆炸数值仿真分析[J].哈尔滨工程大学学报,2006,27（1）：53-56.

[11]Genevieve T.Finite Element Simulation Using SPH Particles as Loading on Typical Light Armoured Vehicles[C].10th International LS-DYNA Users Conference.

[12]Clough R W.Early History of the Finite Element Method from the View Point of a Pioneer[J].International Journal for Numerical Methods in Engineering,2004,60(60):283-287.

[13]李裕春.ANSYS11.0LS-DYNA基础理论与工程实践[M].北京：水利水电出版社,2008：453-458.

[14]王芳,冯顺山.爆炸冲击波作用下靶板的塑性大变形响应研究[J].中国安全学报,2003,13（3）：59-61.

[15]Chen F,Zhang Q,Fei S,et al.Optimization of Ultrasonic Circulating Extraction of Samara Oil from Acer Saccharum Using Combination of Plackett-Burman Design and Box-Behnken Design[J].Ultrasonics Sonochemistry,2017,35(Pt A):161-175.