基于Hammerstein-Wiener模型的地埋管换热器出水温度预测

张长兴，王煜升，刘玉峰，孔祥强，王 清

（1. 山东科技大学，山东省土木工程防灾减灾重点实验室，青岛 266590；2. 山东科技大学机械电子工程学院，青岛 266590；3. 山东科技大学材料科学与工程学院，青岛 266590）

0 引 言

土壤源热泵以浅层大地土壤作为热泵的低位热源，利用土壤作为热泵的吸热与排热的终端，实现空调房间与土壤间的能量转换。地埋管换热器作为土壤源热泵系统与土壤进行能量交换的装置，其换热性能对于系统的运行可靠性和经济性有重要影响。随着土壤源热泵系统工程应用规模的逐渐扩大，系统在低建筑负荷率下能耗较高[1]、长期运行中土壤的热失衡等问题逐渐显现[2]，在一定程度上影响了其推广应用。造成这种现象的原因除了与岩土热物性参数[3-4]、系统设计等因素有关外，更大程度上与系统的运行控制有关[5]。土壤源热泵系统的运行控制是保障系统节能运行的关键。Zhao等[6]通过数值模拟的方法分析了地埋管换热器群组的不同运行模式对土壤热累积效应的影响，结果显示，地埋管换热器分区运行模式可显著缓解由于不平衡的季节负荷所导致的土壤热累积效应。Ma等[7]通过优化地埋管换热器的出水温度，使热泵系统的运行能耗降低了4.2%。地埋管换热器对于建筑冷热负荷的热响应需要根据工程的实际运行状况进行准确预判并提前实施调控，对于缓解系统可能造成的土壤冷热积聚，保障实际工程运行的节能性和可持续性至关重要。

作为土壤源热泵系统的关键部件，传统意义上的地埋管换热器数学模型以能量守恒为基础，进行地埋管换热器的传热分析，在设计工况下指导地埋管换热器的设计计算[8]或进行热泵系统运行特性的动态模拟[9]。地埋管换热器数学模型主要有线热源模型[10]、柱热源模型[8]、duct storage system (DST)模型[9]和各类数值模型[11]，此类通过理论方法建立的数学模型计算精度较高，但由于参数辨识量大，难以满足实时在线化控制的需要。本文结合土壤源热泵系统实际运行中需要实现模型控制的需要，提出了一种面向运行控制的地埋管换热器 Hammerstein-Wiener (H-W)模型，利用地埋管换热器实时的进、出水温度数据进行一定量的参数在线学习、训练和辨识，简化以物理模型为基础的系统模型结构，实现地埋管换热器的H-W模型辨识。利用H-W辨识模型，可把地埋管换热器的非线性控制问题简化为线性模型预测控制问题，满足实时在线优化控制的需求，保障土壤源热泵系统运行的可靠性、节能性和可持续性。

1 地埋管换热器Hammerstein- Wiener模型

与理论建模方法相对应，测试法建模是利用系统的输入数据和输出数据建立系统的数学模型，根据系统在正常运行时记录的输入数据和输出数据，设定系统可能的模型结构，经过一系列的处理和数据运算，进而得出该系统或过程的近似数学模型，该方法也称作系统辨识。辨识模型是以控制论为基础的建模方法，认为研究对象是黑箱或者灰箱，根据输入和输出数据建立对象的数学模型[12]。何献忠[13]采用了具有参数自适应和 Hammerstein模型相结合的控制策略方法，实现生物质酶催化过程中pH 值的非线性控制。彭斐等[14]采用神经动态优化方法作为模型预测控制的动态优化器，获得了基于神经动态优化的模型预测控制方法。在暖通空调系统中，面向系统控制的数学模型已经得到了广泛的应用，取得了较好的节能效果[15-17]。

为满足大型土壤源热泵系统的实际运行调控的需要，开发面向热泵系统控制的地埋管换热器模型是非常必要的。通过在线测试收集系统的实时运行数据，建立输入变量和输出变量之间的数学关系式，为实现系统的最优化运行控制奠定基础。Esen等[18]利用神经网络（artificial neural networks，ANN）模型和自适应神经模糊推理系统（adaptive neuro-fuzzy inference system，ANFIS）模型预测土壤源热泵系统的运行性能。结合土壤源热泵工程案例，Sun等[19]用ANFIS模型和ANN模型对热泵系统的机组COP（coefficient of performance，COP）和系统COP进行了预测和试验验证。利用地埋管换热器的ANN模型[20]，Gang等实施了复合土壤源热泵系统的运行控制，并对热泵系统的运行性能进行了分析[21]，基于ANN模型的预测控制策略显示了较高的节能潜力。对于大型土壤源热泵系统而言，地埋管换热器复杂的换热过程是通过其进、出水温度来表征的，尤其是地埋管换热器的出水温度，对于防止供冷季的土壤热积聚和供热季的源侧循环流体冻结，保障系统运行的可靠性和提高系统的运行效率起着至关重要的作用。考虑到地埋管换热器进、出水温度间的非线性关系，且每一时刻具有唯一的输入值和输出值，本文选用 Hammerstein-Wiener(H-W)模型进行地埋管换热器换热过程的辨识。

1.1 Hammerstein-Wiener(H-W)模型

H-W模型是一种Nonlinearity-Linearity-Nonlin earity（N-L-N）型的非线性模型，由一个无记忆的输入非线性模块f、一个动态线性模块B/F和一个静态的输出非线性模块 h串联而成，其特点是可将静态非线性特性和动态线性特性分开考虑，简单又有效地描述了相当广泛的一类非线性系统，能较好地反映大多数工业生产过程的非线性特性。H-W模型的结构流程图如图1所示。

图1 Hammerstein-Wiener模型的结构图Fig.1 Structure of Hammerstein-Wiener model

图1 中f是转换输入数据u(t)的静态非线性函数，w(t)是非线性输入模块的输出中间变量，与输入数据u(t)有相同的维数，w(t) = f(u(t))；h是将x(t)转换成输出数据y(t)的静态非线性函数，y(t) = h(x(t))；G是转换输入数据w(t)的动态线性系统，x(t)是线性模块的输出中间变量，与输出数据y(t)有相同的维数。

式中 ( a ,···,a )T和 (b ,···,b )T为参数向量，z为传递参1n0 m-1数。 F ( z-1)、 B ( z-1)分别为n和m阶后移算子多项式，d为系统时延。

函数 h具有一对一映射关系时，则存在逆映射x( t) = h-1(y( t) ) = g( y( t ))，故可建立预测模型如式（2）。

式中 y ( t)和yˆ( t)分别为输出的真值和模型预测值，e( t)为真值和预测值的相对误差。

设H-W模型中的参数向量真值为θ = ( a1, ···,an, b0,···,bm-1)T,而 待 辨识模型中 的 参 数估计值为= (, ·· ·,,, ·· ·,)T。此时，H-W模型的辨识问题，转化为利用输入输出观测序列 u(N)和 y ( N )进行估计向量= (,···,, ··,)T的优化问题，优化的目标函数为：

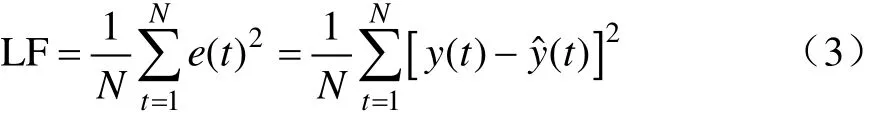
式中N为辨识样本数量，LF为优化的目标函数。

当目标函数值最小时，也可用数据的拟合度判定模型辨识精度的准则

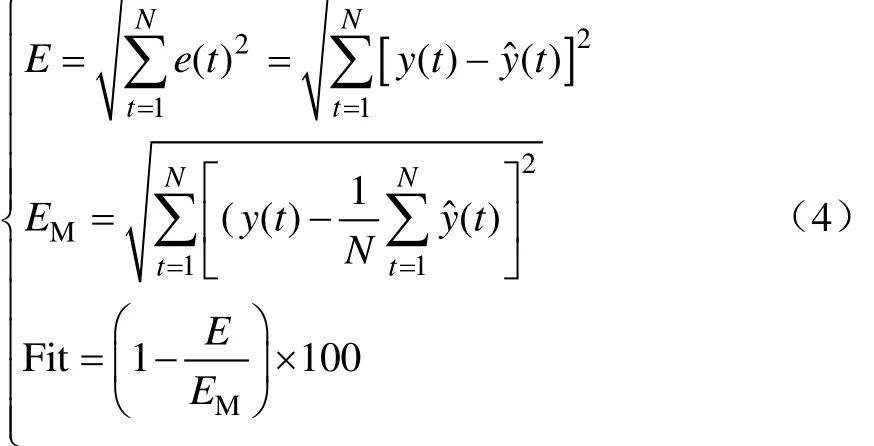
式中E为 ()e t的Euclid范数，EM为真值与预测均值差的Euclid范数，Fit为拟合度。

1.2 地埋管换热器H-W模型

目前，H-W 模型辨识已在循环流化床锅炉床温系统预测、P-S铜转炉吹氧量预测等热工领域中应用[22-23]，满红等[24]利用H-W模型实现了对连续搅拌反应釜的神经网络预测控制。对于地埋管换热器而言（图 2），其物理模型一般以钻孔为界，分成 2个计算区域进行：孔外区域以“柱热源”或“线热源”理论进行非稳态传热计算；孔内区域按照稳态传热计算，通常采用确定热阻的方法进行其传热过程分析。因此，地埋管换热器的传热分析过程非常复杂，难以满足土壤源热泵系统在线预测控制的需要。本文提出的地埋管换热器H-W模型的输入数据为地埋管换热器的进水温度，输出数据为地埋管换热器的出水温度，属于单输入单输出的非线性黑箱模型。与图1的H-W模型结构相对应，即 u ( t) = Tin( t) ; y( t) = Tout(t );地埋管换热器的 H-W 模型辨识和模型验证需要结合其进、出水温度数据进行。辨识过程中，可根据系统控制的需要选择温度取样的时间间隔 ts。当 ts=1 h时，采用一周（168 h）的逐时运行数据进行模型辨识，用2 d（48 h）数据进行辨识模型的验证，以确保H-W模型的精度满足预测控制的需要[25-26]。

图2 地埋管换热器物理模型Fig.2 Physical model of borehole heat exchangers

2 地埋管换热器的H-W模型辨识

根据图1的H-W模型结构，在非线性化的输入模块f和输出模块h中，需要对数据进行非线性处理，本文采用分段线性函数（piecewise linear function）进行，输入输出的断点数量均取为10。对于线性化输入模块G中多项式的阶数取为 m=3，n=4，系统时延 d=0；选用Levenberg-Marquardt（L-M）寻优算法估计参数θ。由于L-M 算法利用了近似的二阶导数信息，比梯度下降（gradient descent）算法提高速度几十甚至上百倍[27]。

地埋管换热器H-W模型的辨识原理如图3所示，θ表示H-W模型的待定系数，设有N个学习样本，期望输出值为 y ( 1),y( 2),y( 3),···,y ( t ) , ···,y ( N)，H-W 模型的输出为yˆ( 1 ),yˆ( 2),yˆ( 3 ) ,···,yˆ ( t ) , ···,yˆ ( N)，学习过程是通过目标函数LF校正模型的系数，使 y ( t)接近yˆ( t)。L-M算法给出H-W模型待定系数的初值，然后根据样本输入u(t)，计算H-W 模型的输出yˆ( t)，对于每一次循环，计算本次循环的目标函数值LF，由L-M算法通过循环迭代确定出H-W模型的最优参数值。

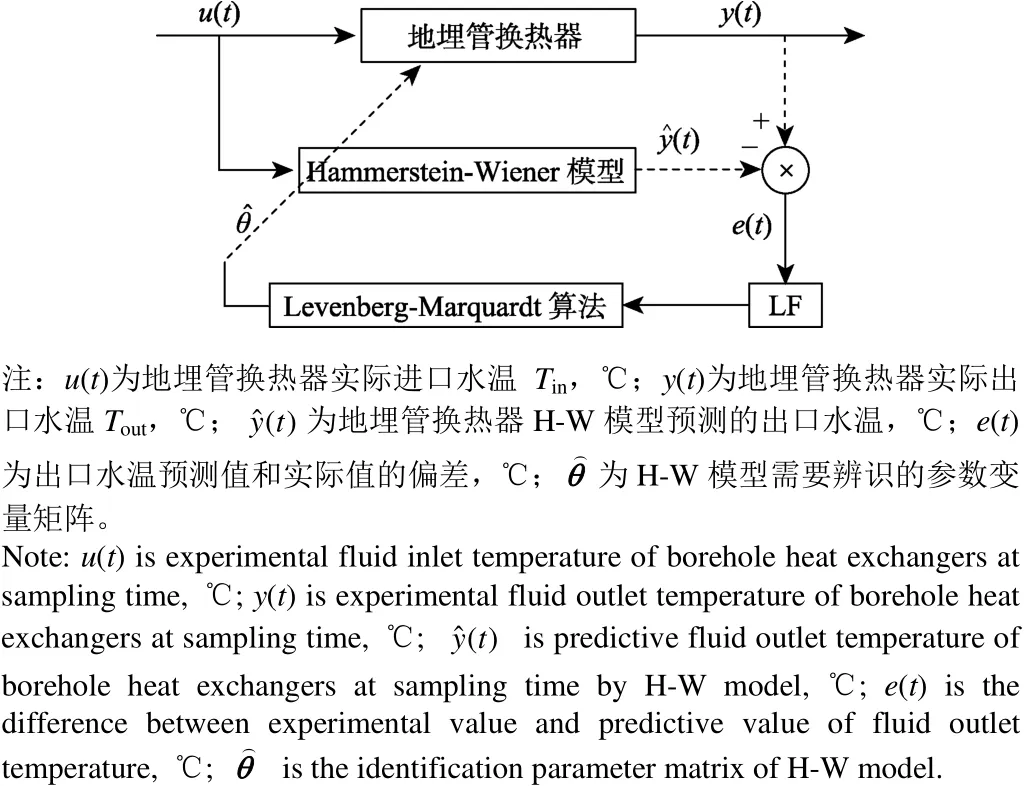
图3 地埋管换热器H-W模型的辨识原理图Fig.3 Identification principle diagram of Hammerstein-Wiener(H-W) model of borehole heat exchangers

3 试验结果与分析

为了验证地埋管换热器 H-W 模型辨识方法的准确性，本文结合文献[28]中地埋管换热器群组进出、水温度模拟值，对最优参数值θ进行识别，地埋管换热器数量为3个，单U型地埋管换热器的参数见表1和表2。考虑到土壤源热泵系统在线控制的需要，用地埋管换热器前168 h的逐时进、出水温度进行H-W模型辨识，后48 h的出水温度用于预测的验证，以检验H-W模型辨识的可靠性。

表1 单U型地埋管换热器相关参数Table 1 Related parameters of single U-pipe borehole heat exchanger

表2 U型管内流体与土壤的相关参数Table 2 Related parameters of fluid in U-pipe and soil

3.1 地埋管换热器H-W模型辨识与验证

用文献中第500～667 h的地埋管换热器的逐时进、出水温度进行H-W模型辨识，在参数寻优过程中，目标函数LF的值由0.337降至5.77×10–6，在第500～667 小时内 ()y t与ˆ()y t的拟合度为99.71%，获得

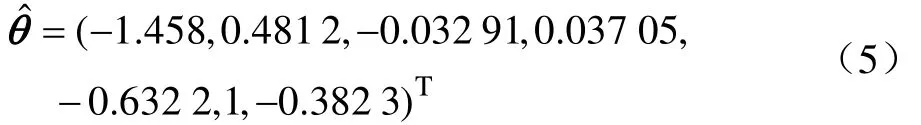
即

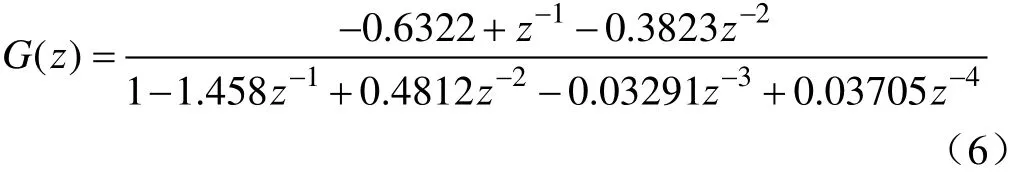
辨识模型中2个非线性模块的分段线性函数f和h变化如图4所示。

根据H-W模型的辨识结果，将第668～715 h的地埋管换热器逐时进水温度作为H-W模型的输入u(t)，将输出的出水温度预测值 y与对应的文献模拟值进行对比。H-W模型中48 h对应的w, x响应如图5所示，H-W模型48 h的动态输出值y对比及误差见图6。可以看出，输入48 h的温度变化数据后，非线性模块f将输入数据u转换为w，w的变化与u的变化趋势保持一致，经线性模块G转换为x后输出y值，地埋管换热器48 h出水温度模型预测值与文献对应值的拟合度为99.44%，预测值的绝对误差仅为10–3数量级，地埋管换热器的H-W模型显示了较高的预测精度。

图4 辨识结果中非线性模块的分段线性函数f和h变化Fig.4 Input function f and output function h corresponding to identification result

图5 H-W模型预测过程中的w, x的变化Fig.5 Dynamic responses of w and x in process of model prediction

图6 48 h动态温度预测值与试验值的对比Fig.6 Comparison of preditive value and experimental value of 48 h dynamic outlet water temperatures

为了进一步验证H-W模型辨识的精度，分别用第72、96、120、144和168小时5个时间段的H-W模型预测值与文献[28]中对应的地埋管出水温度数据进行对比，各时间段对应的拟合度Fit值对比如图7所示。可以看出，与48 h时间段对应的Fit值相比，其后的5个时间段的Fit值有所下降，72 h时段的对应值最低，但仍高于91%，而96 h后的3个时段对应的Fit值均高于95%，说明在较长的运行时间段内仍然能保证H-W辨识模型的预测精度。

3.2 地埋管换热器H-W模型的稳定性

为了验证地埋管换热器H-W模型长期预测结果的准确性，基于H-W模型，用第1～1 167小时的地埋管换热器逐时进水温度进行第168～1 216小时中“48 h出水温度”的逐时预测，并用文献对应值进行验证。模型辨识与验证过程示意图如图8所示。整个过程中需进行1 000次H-W模型的辨识与验证，预测结果的准确性通过1 000个“48 h出水温度”的拟合度Fit值来表示。拟合度Fit值在各区间中的分布如图9所示。拟合度低于80%的占比为9%，拟合度高于95%的占69%，拟合度高于90%的比例占83%，可看出H-W模型的辨识精度较高，对复杂非线性对象有较好的辨识能力，作为全局的N-L-N模型，辨识参数会随地埋管换热器非线性动态进、出水温度的变更而更新，能随时反映地埋管换热器的动态过程，可用于地埋管换热器动态特性的在线预测，满足土壤源热泵系统中地埋管换热器群组的调控需求。

图7 不同时间段模型预测值对应的Fit值对比Fig.7 Comparison of goodness Fit from different validation periods

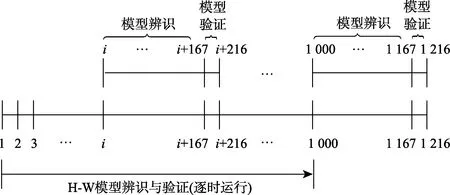
图8 连续1 000次模型辨识与验证过程Fig.8 Process of continuous 1 000-time identification and validation of H-W model

图9 连续1 000次模型验证的拟合度Fit值分布图Fig.9 Distribution of goodness Fit from 1 000-time validation of H-W model

4 结 论

为了实现土壤源热泵系统优化控制，本文提出了一种面向系统控制的地埋管换热器 Hammerstein-Wiener（H-W）模型，并利用既有的地埋管换热器进、出水温度数据进行了H-W模型的辨识与验证。得到以下结论：

1）利用Levenberg-Marquardt（L-M）寻优算法对地埋管换热器H-W模型中的参数向量进行了估计，L-M寻优算法具有收敛速度快，结果准确的特点，适用于地埋管换热器H-W模型的在线辨识。

2）利用既有的168 h的地埋管换热器进、出水温度对H-W模型进行辨识，以此为基础验证了48 h的模型预测结果，预测值与文献对应值的拟合度高达99.44%，H-W辨识模型显示了较高的预测精度。

3）通过连续1 000次的H-W模型辨识与验证的试验表明，48 h出水温度预测值与文献对应值的拟合度高于90%的比例占83%，地埋管换热器H-W模型在线辨识与出水温度预测显示了较强的稳定性。

[1] 张长兴，胡松涛，宋伟，等. 负荷侧回水温度控制在地源热泵供热中的应用研究[J]. 制冷学报，2014，35(5)：19－24.Zhang Changxing, Hu Songtao, Song Wei, et al. Application of load-side return water temperature control strategy in heating operation of ground-coupled heat pump system[J].Journal of Refrigeration, 2014, 35(5): 19－24. (in Chinese with English abstract)

[2] You T, Wu W, Shi W, et al. An overview of the problems and solutions of soil thermal imbalance of ground-coupled heat pumps in cold regions[J]. Applied Energy, 2016, 177(9):515－536.

[3] 张长兴，王德水，刘玉峰，等. 模拟退火算法在岩土热物性参数确定中的应用[J]. 化工学报，2015，66(2)：545－552.Zhang Changxing, Wang Deshui, Liu Yufeng, et al. Application of simulated annealing algorithm for determining parameters of rock-soil thermal properties[J]. CIESC Journal, 2015, 66(2):545－552.(in Chinese with English abstract)

[4] 张长兴，郭占军，刘玉峰，等. 土壤源热泵非稳态热流热响应试验中岩土热物性参数的确定[J]. 农业工程学报，2014，30(12)：192－199.Zhang Changxing, Guo Zhanjun, Liu Yufeng, et al. Determining parameters of rock-soil thermal properties in thermal response test of ground-coupled heat pump under working condition of transient heat flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 192－199. (in Chinese with English abstract)

[5] Chen Y, Chen J, Umberto B, et al. Heat flow balance and control strategies for a large GSHP[J]. Journal of Southeast University, 2013, 29(1): 92－98.

[6] Zhao T, Yu M, Rang H, et al. The influence of ground heat exchangers operation modes on the ground thermal accumulation[J].Procedia Engineering, 2017, 205(10): 3909－3915.

[7] Ma Z, Xia L. Model-based optimization of ground source heat pump systems[J]. Energy Procedia, 2017, 111(3): 12－20.

[8] Cullin J R, Spitler J D, Montagud C, et al. Validation of vertical ground heat exchanger design methodologies[J].Science and Technology for the Built Environment, 2015,21(2): 137－149.

[9] Zhang C, Hu S, Liu Y, et al. Optimal design of borehole heat exchangers based on hourly load simulation[J]. Energy, 2016,116(12): 1180－1190.

[10] 张长兴，郭占军，刘玉峰，等. 模式搜索算法在地埋管换热器热阻确定中的应用[J]. 农业工程学报，2013，29(21):182－187.Zhang Changxing, Guo Zhanjun, Liu Yufeng, et al. Application of pattern search algorithm for determining heat resistance of ground heat exchanger[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013,29(21): 182－187. (in Chinese with English abstract)

[11] Monzó P, Mogensen P, Acuña J, et al. A novel numerical approach for imposing a temperature boundary condition at the borehole wall in borehole fields[J]. Geothermics, 2015,56(7): 35－44.

[12] 森发. 复杂系统建模理论与方法[M]. 南京：东南大学出版社，2005.

[13] 何献忠. 生物质酶催化过程中 pH 值的非线性控制[J]. 农业工程学报，2013，29(10)：213－218.He Xianzhong. Nonlinear control of pH value in biomass catalytic process[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013,29(10): 213－218. (in Chinese with English abstract)

[14] 彭斐，彭勇刚，韦巍. 基于神经动态优化的人工气候箱温湿度模型预测控制[J]. 农业工程学报，2014，30(9)：176－182.Peng Fei, Peng Yonggang, Wei Wei. Model predictive control of temperature and humidity of artificial climate chest based on neuro dynamical optimization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(9): 176－182. (in Chinese with English abstract)

[15] Zeng Y, Zhang Z, Kusiak A. Predictive modeling and optimization of a multi-zone HVAC system with data mining and firefly algorithms[J]. Energy, 2015, 86(6): 393－402.

[16] Afram A, Janabi-sharifi F. Black-box modeling of residential HVAC system and comparison of gray-box and black-box modeling methods[J]. Energy and Building, 2015, 94(5):121–149.

[17] Zakia A, Gm S, Tania U, et al. Modeling techniques used in building HVAC control systems: A review[EB/OL].[2017-12-12] https://doi.org/10.1016/j.rser. 2017.10.044.

[18] Esen H, Inalli M. ANN and ANFIS models for performance evaluation of a vertical ground source heat pump system[J].Expert Systems with Applications, 2010, 37(12): 8134－8147.

[19] Sun W, Hu P, Lei F, et al. Case study of performance evaluation of ground source heat pump system based on ANN and ANFIS models[J]. Applied Thermal Engineering,2015, 87(8): 586－594.

[20] Gang W, Wang J. Predictive ANN models of ground heat exchanger for the control of hybrid ground source heat pump systems[J]. Applied Energy, 2013, 112(12): 1146－1153

[21] Gang W, Wang J, Wang S. Performance analysis of hybrid ground source heat pump systems based on ANN predictive control[J]. Applied Energy, 2014, 136(11): 1138－1144.

[22] 桂卫华，宋海鹰，阳春华. Hammerstein-Wiener 模型最小二乘向量机辨识及其应用[J]. 控制理论与应用，2008，25(3)：393－397.Gui Weihua, Song Haiying, Yang Chunhua. Hammerstein-Wiener identified by least-squares-support-vector machine and its application[J]. Control theory & applications, 2008, 25(3):393－397. (in Chinese with English abstract)

[23] 刘长良，任燕燕，王东风，等. 热工系统 Hammerstein-Wiener 模型辨识[J]. 计算机仿真，2013，30(9)：394－397.Liu Changliang, Ren Yanyan, Wang Dongfeng, et al.Identification of thermal process using Hammerstein-Wiener model[J]. Computer Simulation (Transactions of the CSAE),2013, 30(9): 394－397. (in Chinese with English abstract)

[24] 满红，邵诚. 基于 Hammerstein-Wiener 模型的连续搅拌反应釜神经网络预测控制[J]. 化工学报，2011，62(8):2275－2280. (in Chinese with English abstract)Man Hong, Shao Cheng. Neural network predictive control of continuous stirred-tank reactor based on Hammerstein-Wiener Model[J]. CIESC Journal, 2011, 62(8): 2275－2280.

[25] Verhelst C. Model Predictive Control of Ground Coupled Heat Pump Systems in Office Buildings[D]. Leuven:University of Leuven, 2012.

[26] Atam E, Schulte D O, Arteconi A, et al. Control-oriented modeling of geothermal borefield thermal dynamics through Hammerstein-Wiener models[J]. Renewable Energy, 2018,120(5): 468－477.

[27] Marquardt D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431－441.

[28] 张长兴，郭占军，刘玉峰，等. 土壤源热泵系统运行特性的快速预测方法[J]. 农业工程学报，2012，28(24)：173－178.Zhang Changxing, Guo Zhanjun, Liu Yufeng, et al. A fast forecast method for operation characteristics of groundcoupled heat pump system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(24): 173－178. (in Chinese with English abstract)