淡季中酒店与OTA合作模式选择研究

林雅琴，郭 强，张志文，赵 达

(1.海南大学旅游学院，海南 海口 570228；2.海南大学科研处，海南 海口 570228；3.海南寰岛酒店旅游投资有限公司，海南 海口 570208；4.海南大学经济与管理学院，海南 海口 570228)

1 引言

酒店业具有固定投资成本高、市场需求波动性大、客房服务产品不可储存等特性，因此入住率对其收益和投资回报很重要。但由于淡季时入住率下降，酒店收益难获得，投资回收周期难缩短。故而，提高淡季客房入住率以缓解该困境，是酒店迫待实现的重要目标。而酒店收益管理对入住率提高问题的研究，则为实现这一目标提供了重要思路。此外，加强与OTA合作，是酒店实现这一目标的重要途径[1-4]。随着“互联网+”时代的到来，OTA“大数据”等特征优势日益凸显，市场吸引力不断增强，能够为酒店提供丰富的市场资源[5-8]。Toh、Dekay和Raven调查发现：酒店客房的在线预订顾客中，高达30%会选择OTA[8]。

而目前酒店与OTA的常见合作模式，主要有净价模式(The merchant model)和佣金模式(又称委托代理模式，The agent model)[2,8-10]。两模式的具体合作过程不同。净价模式的合作过程一般如下：OTA先以协议价购买酒店部分客房在某期间的使用权，随后定价出售给OTA网站顾客，赚取协议价与出售价间的差价，酒店则赚取协议价收入[2,8-9]。佣金模式的合作过程一般如下：酒店委托OTA售房，并根据OTA网站的实际客房销售收入，支付OTA一定比例的佣金，赚取佣金与网站客房售价间的差价，OTA则赚取佣金收入[2,8,10]。那么，这两种合作模式孰优孰劣，酒店和OTA该如何正确选择？这是非常有意义并值得深究的一个问题。研究该问题，有利于协调由酒店和OTA构成的酒店服务供应链，以及提高酒店整体效益，从而进一步缓解酒店淡季时的销售困境；同时也有利于OTA增加收益。

因而，本文结合收益管理理论和供应链管理理论，利用Stackelberg博弈模型，研究了淡季时不同情境下净价模式和佣金模式何者更优的问题，即酒店和OTA的合作模式选择问题。

与本文相关的文献主要有两类：(1)双渠道供应链协调与优化研究；(2)净价模式和佣金模式中酒店与OTA的合作问题研究。目前第一类文献很多，主要集中在制造业方面。比如，陈树桢、熊中楷和梁喜[11]通过组合两部定价合同和促销水平补偿合同，协调了双渠道供应链；禹爱民和刘丽文[12]在随机需求和联合促销情况下，研究了双渠道供应链系统上的制造商和零售商之间的价格竞争和协调问题；但斌、徐广业和张旭梅[13]通过补偿策略，协调了电子商务环境下的双渠道供应链；同年，徐广业和但斌[14]利用价格折扣模型再次研究了电子商务环境下的双渠道供应链协调问题；随后，但斌和徐广业[15]运用报童问题的分析框架，建立了能够协调双渠道供应链的两方收益共享契约模型。相比制造业方面，旅游等服务业方面的双渠道供应链协调与优化研究起步晚，成果稀缺，而且这方面研究还要考虑旅游等服务业存在的无库存成本，产能约束等特征。而酒店和OTA的合作问题研究，就属于双渠道旅游供应链协调与优化问题的研究范畴。只是目前研究酒店和OTA合作问题的文献并不多，而具体研究净价模式和佣金模式中酒店和OTA合作问题的文献更是屈指可数。其中，董玉凤[2]和Anderson等[16]均研究了净价模式和佣金模式；而叶飞等[17]、杜菲[18]和蒲徐进等[19]仅研究了佣金模式。董玉凤[2]利用Stackelberg博弈模型，研究了净价模式中旅行套餐客房分配策略，以及佣金模式中一家酒店与多家OTA的客房分配和超售策略。Anderson和Marcus[16]研究了“无风险房”(类似佣金模式)和“有风险房(类似净价模式)”中一家酒店对多家OTA的客房销量控制问题。叶飞[17]通过借鉴文献[20]，在考虑网上退订和酒店超定的前提下，研究了佣金模式中一家酒店与一家OTA合作时酒店超定量和给OTA的客房预留量问题，探讨了佣金率与市场需求不确定性对酒店决策的影响。杜菲[18]利用Stackelberg博弈模型，分析了佣金模式中OTA的市场占有率和市场影响力对分散决策时酒店和OTA合作产生的影响。蒲徐进和杜晓东[19]通过营销努力成本分担机制，协调了由一家酒店和一家OTA构成的酒店服务供应链。不过，这些文献均只是研究了单一模式下酒店和OTA的客房分配、超售策略或供应链协调等问题，并未涉及酒店和OTA的合作模式选择问题。本文研究则弥补了以往研究在这一方面的空缺，具有很强的理论意义。

本文接下来的具体研究思路如下：先是分别对净价模式和佣金模式中的酒店和OTA最优控房的关键决策变量进行分析，得到最优决策结果，以及酒店和OTA各自最优利润；基于此，在几种常见情境下，对酒店和OTA的最优合作模式选择问题展开研究，演示酒店和OTA的具体决策过程，并利用图解法和数值模拟分析法，得到最优结果。

2 问题描述及符号说明

本文仅针对实践中还未确定合作模式的一家酒店与一家OTA的合作模式选择问题进行研究。因为是预判分析，所以无需考虑净价模式和佣金模式间的转换成本问题。不过，若实践中酒店与OTA已事先确定合作模式，那么进行合作模式切换时就需要考虑有可能产生的额外成本。

虽然在数学本质上净价模式和佣金模式不同，但在实践中，除了决策的主导权可能不同外，这二者的适用条件并无差别。本文假设净价模式中OTA占决策主导权；佣金模式中酒店占决策主导权。其理由如下：(1)净价模式中，淡季时酒店面临客房入住率下降的困境会增强OTA的话语权，而且由于OTA须承担事先以协议价获取的客房的全部销售风险，其也会想方设法获取决策主导权；(2)佣金模式中，因酒店在淡季本就面临低入住率和低收益的困境，并且还要承担客房的全部销售风险，所以为了降低风险的同时提升利润空间，酒店会想方设法获得决策主导权。

OTA网站的客房需求量与其营销努力(比如对该酒店的网页显示、网页排版等)相关[21-22]，而酒店客房的预订情况也会受该因素影响[23]。因此本文把OTA营销努力因素内置于模型，并假设它对OTA网站客房销量的提高有正向影响[24]。此外，出于对现实中酒店和OTA售价差别的考虑，本文假设OTA网站客房售价低于或等于酒店自营渠道客房售价[19]。而由于酒店淡季客房入住率低导致房源充足，本文不考虑超售情况[2]，并假设在淡季合作时酒店会优先满足OTA网站的顾客订房需求。后者假设主要还考虑了另一现实情况：当前大部分酒店已患有“OTA依赖症”，这一症状在淡季尤为严重[5-8]。“界面新闻”就曾在报道中提到：国外调查机构PhoCusWright的数据显示，中国酒店市场上十个人中有九个人会选OTA订房，仅少于四成的用户会使用酒店官网；中小酒店患上了“OTA依赖症”，比如，承德初见客栈旺季线上订单占七成，淡季则占到了九成；因为需要OTA带来新客源，所以在面对OTA联手抬高佣金价格时，酒店也很可能妥协。

为方便论述，对本文涉及的符号定义如下：Q为酒店可售房总量；j=1,2，1表示净价模式，2表示佣金模式；πHj为酒店期望利润；πOj为OTA期望利润；PH为酒店自营渠道客房售价；POj为OTA网站客房售价，在净价模式中是OTA的决策变量，但在佣金模式中是酒店的决策变量；bj为OTA营销努力成本，是OTA的决策变量；w为客房协议价，它和φ分别是酒店在净价模式和佣金模式中的决策变量；φ为客房佣金比例(0<φ<1)；CH为酒店每间客房的变动成本；SOj为OTA的预期市场需求量；SHj为酒店自营渠道的预期市场需求量；θ为投入营销努力成本后通过OTA网站浏览酒店信息但未在网站订房的顾客比例(0<θ<1)；λ为单位营销努力成本投入带来的需求变动效率(0<λ<1)；β为OTA营销努力成本投入对顾客订房量的影响程度(0<β≤1)。λ与β有可能存在内部的关联性，且可能是呈明显的正相关关系，但为了简化模型，本研究暂不考虑二者的具体相关关系。同时为了简化分析，我们进一步假设：

(1)酒店与OTA是平等独立且完全理性和风险中性，当任意一方的期望收益为负，将退出博弈；

(2)OTA营销努力的成本是可预见的，是营销努力水平的递增凸函数[24-25]，而OTA营销努力投入带来的需求增长量是关于营销努力成本的函数；

(3)酒店与OTA是基于信息完全对称情况下进行分散决策的；

(4)不考虑酒店与OTA的固定成本、预订未到、预订取消、网上退订等情况；

借鉴文献[19]中的需求模型，本文假设：

SOj=E(X|bj)=α+(1-θ)βbjλ+ε

(1)

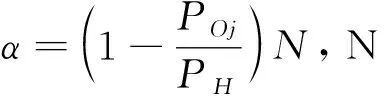
模型假设中Δ=αe的缺陷：当营销努力投入无限增大时，市场需求增长量将无限增大。蒲徐进和杜晓东[19]中的α表示营销努力效果系数，e表示OTA营销努力。

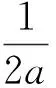
(2)

其中t=Q+a-μ。

由式(2)发现，SHj≤Q-SOj恒成立，说明淡季时酒店自营渠道不会缺房，这也基本符合现实。

3 净价模式中酒店和OTA最优策略选择

根据净价模式的一般合作过程及上述假设， OTA与酒店的期望利润分别表示为：

πO1=PO1SO1-wSO1-b1=

(PO1-w)[α+(1-θ)βb1λ]-b1

(3)

πH1=PHSH1+wSO1-CHQ=(PH-CH)Q-

(4)

(5)

从式(5)可以得到结论1。

结论1b1*与w呈负相关；与PO1呈正相关。说明在淡季时，为提高OTA的在线营销的积极性以提高入住率，酒店会尽量降低客房协议价；而随着PO1的提高，为保证网站客房销量的稳定或提高，OTA会加大营销力度。

将式(5)代入式(4)，求偏导得到：

(6)

其中γ=β2(1-θ)2。

(7)

将式(7)代入式(5)得到：

(8)

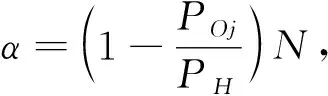
(9)

(10)

{4a2(6N-PHγ)(2N+PHγ)+2aPHγ[8N2+PHγt-2Nt]+N2γ2PH2}

(11)

由此得到：

w*=PO1*+

(12)

b1*=

(13)

(14)

πO1*=(PO1*-w*)SO1*-b1*

(15)

(16)

从式(11)、(12)、(13)可以得到结论2-6。

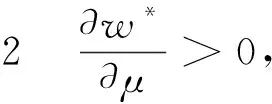
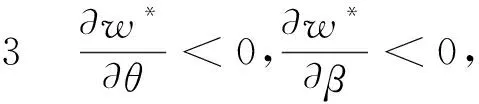
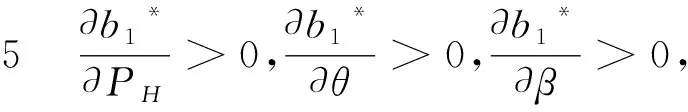
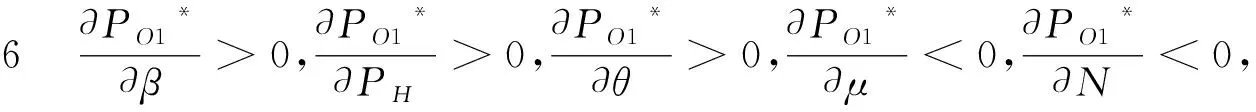
上述结论1-6为选择净价模式为既定合作模式的酒店和OTA提供了合作决策的理论基础和探索性思路。净价模式中OTA网站最优客房售价、OTA最优营销努力成本、最优客房协议价、酒店和OTA各自的最优期望利润分别如式(11)、(13)、(12)、(16)和(15)所示。该最优结果将被用于后文酒店和OTA的合作模式选择分析。

4 佣金模式中酒店与OTA最优策略选择

根据佣金模式的一般合作过程及前文假设条件，佣金模式中酒店与OTA的期望利润分别表示为：

πO2=φPO2SO2-b2=φPO2[α+(1-θ)βb2λ]-b2

(17)

(18)

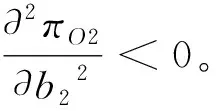
(19)

从式(19)可以得到结论7。

结论7b2*与φ、PO2呈正相关，说明φ和PO2的提高利于激发OTA的在线营销积极性。

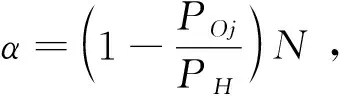
(20)

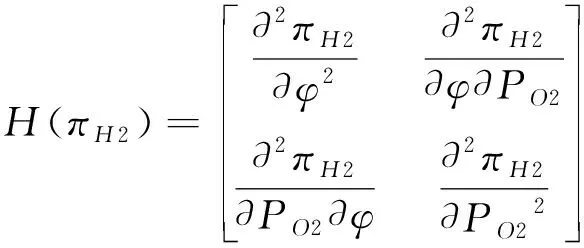
(21)

由于式(21)比较复杂，难以求出具体解析式。为便于分析且不影响研究结论，我们同样假设λ=1/2。由一阶条件得到最优客房佣金比例：

φ*=φ(PO2)=

(22)

将式(22)代入式(19)得到：

b2*=

(23)

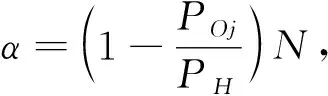
(24)

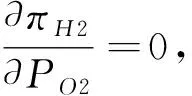
(25)

由此得到：

φ*=

(26)

b2*=

(27)

(28)

πO2*=φ*PO2*SO2*-b2*

(29)

(30)

由式(25)、(26)、(27)得到以下3条结论：

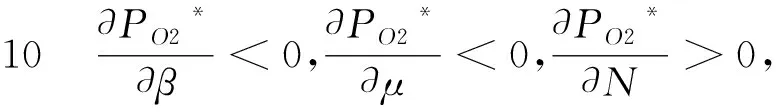
结论7-10为选择佣金模式为既定合作模式的酒店和OTA提供了合作决策依据和探索性思路。佣金模式中，OTA网站最优客房售价、OTA最优营销努力成本、最优客房佣金比例、酒店和OTA各自最优期望利润分别如式(25)、(27)、(26)、(30)和(29)所示。该最优结果也将被用于接下来的不同情境中酒店和OTA的合作模式选择分析。

5 酒店与OTA的最优合作模式选择

令ΔπH=πH1*-πH2*，ΔπO=πO1*-πO2*。根据完全理性人假设，我们可通过判断ΔπH和ΔπO的大小，确定酒店和OTA各自的最优合作模式选择结果。当ΔπH=0时，酒店选净价模式和选佣金模式无差别；当ΔπH>0时，酒店选净价模式更优；当ΔπH<0时，酒店选佣金模式更优。而OTA的合作模式选择原理与之一致。由此得到酒店和OTA达成一致协议时的最优合作模式选择依据，如表1所示。除了表1的所有情况外，酒店和OTA在合作模式选择问题上均无法达成一致协议，需双方作进一步协商。

表1 酒店和OTA达成协议时的最优合作模式选择依据

由于前文在净价模式和佣金模式中得到的最优结果的解析式比较复杂，所以本文接下来基于表1的判断依据，借助数值模拟分析法，对酒店和OTA的合作模式选择问题作进一步分析，确定最优结果。

由式(15)、(16)、(29)和(30)，我们可初步推断：影响酒店和OTA合作模式选择的因素有PH、μ、β、θ和N。但由于酒店自营渠道客房售价一般由市场竞争决定；经大量的数值仿真模拟发现，PH的变动不影响酒店和OTA的合作模式选择结果；现实中θ值波动性大，难预测(本文给的θ值仅供参考)，并且在短期内酒店和OTA的合作协议不会因θ值的变动而频繁更改，所以本文仅探讨β和N二者变动对酒店和OTA的最优合作模式选择结果的影响。

假设各参数特征值：Q=200，PH=200，CH=50，a=50，μ=60，θ=0.25。为了更直观的判断酒店和OTA最优的合作模式选择结果，我们引入了三维图方法。该方法的具体判断步骤如下：

(1)利用Mathematica7.0软件，分别作出πO1和πO2的复合三维图，以及πH1和πH2的复合三维图，如图1和图2所示。这里的复合三维图，是指两个三维图被同时放在一个立体空间里。

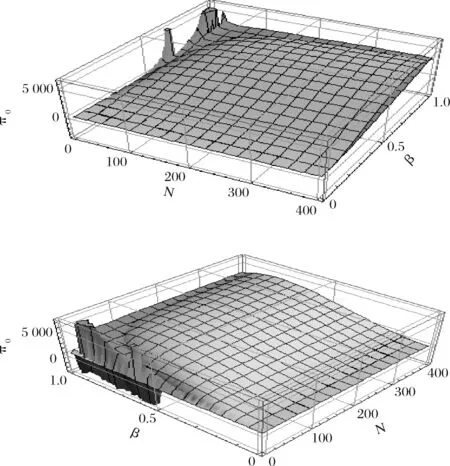
图1 πO1和πO2的复合三维图(深色阴影部分为πO1的三维图)

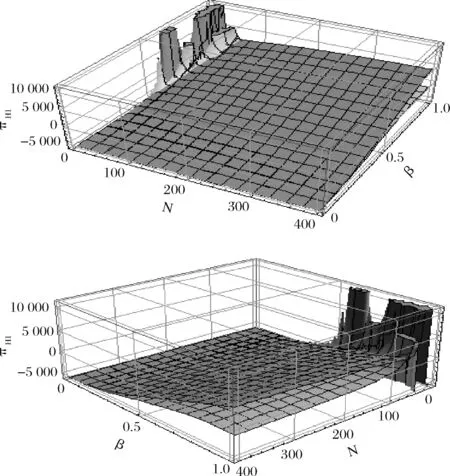
图2 πH1和πH2的复合三维图(深色阴影部分为πH1的三维图)

(2)将N和β的预测值代入图1和图2。通过分别比较两模式中酒店和OTA各自的最优期望利润，确定二者所选的最优合作模式。由图1和图2发现：在可行域πO1，πH1，πO2，πH2∈(0,+∞)，大部分情况下，OTA倾向于选择佣金模式，而酒店则相反。

(3)根据酒店和OTA各自的合作模式选择结果，判断二者能否达成一致协议。若能，则确定双方的最优合作模式；否则，需要双方作进一步协商。结合图1和图2发现：达成一致合作协议时，二者选择的最优合作模式几乎都是净价模式。

当然，我们也可根据N和β的预测值，先分别计算净价模式和佣金模式中酒店和OTA各自的最优期望利润，而后比较得到双方的最优合作模式选择结果。不过，该方法计算过程复杂，且不够直观明了，尤其是当N和β的预测值是一个范围时，计算更复杂。而三维图方法则可省去大量计算，简单明了。

图3 πO和πH的三维图之俯视图(深色阴影部分表示净价模式)

为进一步验证三维图方法判断结果的可靠性，我们还进行了具体的算例分析。假设N和β的预测值分别为68和0.95。由图1和图2得到其俯视图，如图3所示。图3中，左图是图1的俯视图；右图是图2的俯视图。由图3观察得知，酒店与OTA都会选择净价模式，二者可达成一致协议。而根据第二种方法计算得到：πO1=2944.42，πH1=1359.8，πO2=1543.76，πH2=11.42，ΔπO>0，ΔπH>0。由此可知：酒店和OTA也都会选择净价模式，二者也可达成一致协议，此时PO1*=188.45，b1*=2403.87，w*=51。可见，三维图方法的判断结果是正确的。

酒店和OTA在实践中完全可根据决策需要，将上述的三维图拓展至多维图，且无论如何都可得到数值解。而本文仅仅是为了展示方便，用三维图作示范。

6 结语

本文建立了需求模型，利用Stackelberg博弈模型及其图解法，对淡季时不同情境下酒店和OTA的最优合作模式选择进行了研究，利用数值模拟法得到了具体的数值解，给出了酒店和OTA最优结果，进一步提高了酒店淡季时的入住率和收益。本文不但为酒店和OTA提供了具有操作意义上的合作模式决策支持，而且更重要的是协调了酒店服务供应链，在提高酒店整体效益的同时，也增加了OTA的收益。此外，研究所使用的博弈模型综合了供应链管理和酒店收益管理因素，弥补了以往研究在酒店和OTA合作模式的对比、选择与优化方面的空缺，为学者们今后的相关研究提供了参考。

由于本文在讨论酒店和OTA合作模式选择时主要采用的是数值模拟法，所以并不能保证研究结果和研究结论完全正确且具有普遍适用性。此外，本文是基于一家酒店与一家OTA的博弈模型来研究二者的合作模式选择问题，而实践中通常会出现一家酒店与多家OTA、多家酒店与一家OTA或多家酒店与多家OTA的合作情况。而且，现实中由于各因素的影响，会出现信息不对称或双方决策者不完全理性等情况。因而，在后续研究中，我们会对这些情况展开更为深入且实际的探讨，同时还可能考虑超订、预订未到、预订取消、网上退订、多日停留和连续入住等部分情况。

参考文献：

[1] Pan Bing, Zhang Lixuan, Law R. The complex matter of online hotel choice[J]. Cornell Hospitality Quarterly, 2013, 54(1): 74-83.

[2] 董玉凤. 与在线旅行社合作背景下酒店的收益管理研究[D]. 合肥: 中国科学技术大学, 2015.

[3] Ma Caiwei. E-collaboration: A university key to solve fierce competition in tourism industry?[J]. International Business Research, 2009, 1(4): 65-71.

[4] Kim D J, Kim W G, Han J S. A perceptual mapping of online travel agencies and preference attributes[J].Tourism Management, 2007, 28(2): 591-603.

[5] Xu Liang, He Ping, Hua Zhongsheng. A new form for a hotel to collaborate with a third-party website: setting online-exclusive-rooms [J]. Asia Pacific Journal of Tourism Research, 2014, 20(6): 1-21.

[6] Law R, Cheung C. A study of the perceived importance of the overall website quality of different classes of hotels[J]. International Journal of Hospitality Management, 2006, 25(3): 525-531.

[7] Anderson C K. Search, OTAs, and online booking: An expanded analysis of the billboard effect[R]. Research Report Cornell Center for Hospitality, 2011.

[8] Toh R S, Dekay C F, Raven P. Travel planning: Searching for and booking hotels on the internet[J]. Cornell Hospitality Quarterly, 2011, 52(52): 388-398.

[9] Connor P O, Murphy J. Research on information technology in the hospitality industry[J]. International Journal of Hospitality Management, 2004, 23(5): 473-484.

[10] Tse A C. Disintermediation of travel agents in the hotel industry[J]. International Journal of Hospitality Management,2003, 22(4): 453-460.

[11] 陈树桢, 熊中楷, 梁喜. 补偿激励下双渠道供应链协调的合同设计[J]. 中国管理科学, 2009, 17(1): 64-75.

[12] 禹爱民, 刘丽文. 随机需求和联合促销下双渠道供应链的竞争与协调[J]. 管理工程学报, 2012, 26(1): 151-155.

[13] 但斌, 徐广业, 张旭梅.电子商务环境下双渠道供应链协调的补偿策略研究[J].管理工程学报, 2012, 26(1): 125-130.

[14] 徐广业, 但斌.电子商务环境下双渠道供应链协调的价格折扣模型[J]. 系统工程学报, 2012, 27(3): 344-350.

[15] 但斌, 徐广业. 随机需求下双渠道供应链协调的收益共享契约[J]. 系统工程学报, 2013, 28(4): 514-521.

[16] Anderson C K, Marcus B. Tour operator revenue management-Competitive supply chain contracting[J]. Journal of Revenue & Pricing Management, 2015, 14(4): 245-261.

[17] 叶飞, 陆木蕊, 廖鹏. “酒店+OTA”双渠道供应链超定策略研究[J]. 运筹与管理, 2015, 24(2): 38-43.

[18] 杜菲. 酒店与旅行社的竞争与协调[D]. 合肥:中国科学技术大学, 2015.

[19] 蒲徐进, 杜晓东. “酒店+OTA”双渠道供应链的销售策略和协调机制研究[J]. 江南大学学报, 2016, 15(1): 112-118.

[20] 陈剑, 肖勇波, 刘晓玲. 航空公司与旅行社的协作机制研究[J]. 中国管理科学, 2004, 12(3): 107-114.

[21] 张菊亮, 陈剑. 销售商的努力影响需求变化的供应链的合约[J]. 中国管理科学, 2004, 12(4): 50-56.

[22] 曲道刚, 郭亚军. 分销商需求与其努力相关时混合渠道供应链协调研究[J]. 中国管理科学, 2008, 16(3): 89-94.

[23] Anderson C K. The billboard effect: Online travel agent impact on Non-OTA reservation[R]. Research Report, Cornell Center for Hospitality，2009.

[24] Guo Xiaolong, Zheng Xiabing, Ling Liuyi, et al. Online coopetition between hotels and online travel agencies: From the perspective of cash back after stay[J].Tourism Management perspectives, 2014, 12(12): 104-112.

[25] Huang Zhimin, Li S X. Co-op advertising models in manufacture-retailer supply chains: A game theory approach[J].European Journal of Operational Research, 2001, 135(3): 527-544.

[26] 赵秋红, 朱少楠, 李安楠. 存在顾客购买转移的双分销渠道订货与库存转运策略[J]. 系统工程理论与实践, 2014, 34(6): 1453-1461.

[27] 曹晓刚, 郑本荣, 闻卉. 考虑顾客偏好的双渠道闭环供应链定价与协调决策[J]. 中国管理科学, 2015, 23(6): 107-117.

[28] Amiri A. Designing a distribution network in a supply chain system: Formulation and efficient solution procedure[J]. European Journal of Operational Research, 2006, 171(2): 567-576.

[29] Guo Xiaolong, He Lina. Tourism supply-chain coordination: the cooperation between tourism hotel and tour operator[J]. Tourism Economics, 2012, 18(6): 1361-1376.

[30] 王小龙, 刘丽文. 竞争型双渠道供应链协调问题研究[J]. 系统工程报, 2009, 24(4): 430-437.