巧用类比，学好一元一次不等式

◎袁冬华

不等式是刻画现实世界中量与量之间不等关系的有效数学模型.一元一次不等式是表示不等关系的最基本的工具，是同学们学习其他相关数学知识的基础，倍受广大命题者的青睐，并成为中考的热门考点之一.学习本章内容时，同学们若能与等式的性质、一元一次方程、一元一次方程的解法、利用方程（组）分析解决实际问题等有明显对应关系的知识联系起来学，了解它们的联系与区别，便会有新的提高.

一、不等式的基本性质VS等式的基本性质

不等式的性质是对不等式进行变形的重要依据，要特别注意会使不等号方向改变的变形.不等式两边乘同一个数，实际上有3种情况：乘同一个正数，乘0，乘同一个负数.当不等式的两边都乘0时，不等式变为等式.不等式性质1类似等式性质1，不等号的方向不改变；不等式性质2中不等式两边都乘（或除以）同一个负数，不等号的方向改变，这是不等式独有的性质，也是初学者易错的地方，因此要特别注意.

例1 下列等式变形错误的是（ ）.

A.由a=b得a+5=b+5

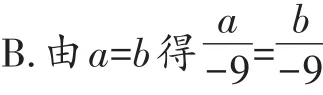
C.由x+2=y+2得x=y

D.由-3x=-3y得x=-y

【解析】A.∵a=b，由等式性质1，等式两边同时加5，得a+5=b+5，正确；

B.∵a=b，由等式性质2，等式两边同时除以-9，得=，正确；

C.∵x+2=y+2，由等式性质1，等式两边同时减去2，得x=y，正确；

D.∵-3x=-3y，由等式性质2，等式两边同时除以-3，得x=y，该选项错误.故选D.

【点评】本例重在考查等式的性质.

例2 已知a＜b，则下列四个不等式中不正确的是（ ）.

A.4a＜4b B.-4a＜-4b

C.a+4＜b+4 D.a-4＜b-4

【解析】依据不等式性质2，由a＜b，可知4a＜4b，故A正确；

依据不等式性质2，由a＜b，得-4a＞-4b，故B不正确；

依据不等式的性质1，可得a+4＜b+4，a-4＜b-4，故C、D正确.故选B.

【点评】本例重在考查不等式的性质，特别是性质2，两边同乘（或除以）同一个负数时，一定要改变不等号的方向！

二、一元一次不等式的解集VS一元一次方程的解

方程的解、不等式的解、不等式的解集，这3个定义的相同点是定义方式相同，解的表示方法也相同.不同点是解的个数不同.一般地，一个不等式有无数个解，而一个方程只有一个或几个解，例如，x=1能使不等式3x＞1成立，那么x=1是不等式的一个解，类似地x=1，2，3，4…也能使不等式3x＞1成立，它们都是不等式3x＞1的解.事实上，当x取大于的数时，

不等式3x＞1都成立，所以不等式3x＞1有无数多个解，不等式3x＞1的解集是x＞

例3 已知关于x的方程（1-a）x=3，其中a≠1，求方程的解.

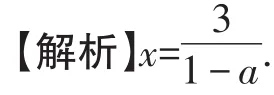
【点评】根据解一元一次方程的步骤，把系数化为1.

例4 已知关于x的不等式（1-a）x＞3的解集为x＜，则a的取值范围是 .

【解析】由不等式性质，可知1-a＜0，

∴a＞1.

【点评】注意到不等号方向已发生改变，根据不等式的性质，可判断1-a＜0，由此可求出a的取值范围.

三、解一元一次不等式的步骤VS解一元一次方程的步骤

【解析】去分母，得2（2x-1）-24=-3（x+4）.

去括号，得4x-2-24=-3x-12.

移项、合并同类项，得7x=14.

两边都除以7，得x=2.

【点评】在学习一元一次不等式之前，我们已经学习了解一元一次方程.它的解法步骤是：（1）去分母；（2）去括号；（3）移项；（4）合并同类项；（5）把系数化为1.

【解析】去分母，得2（2x-1）-24＜-3（x+4）.

去括号，得4x-2-24＜-3x-12.

移项、合并同类项，得7x＜14.

两边都除以7，得x＜2.

【点评】解一元一次不等式的一般步骤与解一元一次方程的一般步骤类似，在解题过程中要体会类比、化归的数学思想方法.在不等式两边都乘（或除以）同一个不等于0的数时，必须根据这个数是正数还是负数，正确地运用不等式的基本性质2.特别要注意，在不等式两边都乘（或除以）同一个负数时，要改变不等号的方向.当然，如果不能确定同乘（或同除）的数的符号时，就要进行讨论.所以只要掌握它们之间的相同点与不同点，那么新知便变成了旧知，易于理解和掌握.

【点评】先去分母，再移项、合并同类项，然后根据不等式的性质求解集，最后将解集在数轴上表示出来即可.

四、一元一次不等式的应用VS一元一次方程的应用

例7 如图，用火柴棒按以下方式搭“小鱼”.

（1）搭n条“小鱼”需要火柴棒多少根？

（2）计算搭12条“小鱼”需要多少根火柴棒？

（3）若搭n朵某种“小花”需要火柴棒（3n+20）根，现有一堆火柴棒，可以全部用上搭出m条“小鱼”，也可以全部用上搭出m朵“小花”，求m的值及这堆火柴棒的数量.

【解析】（1）搭n条“小鱼”需要火柴棒的数量为8+6（n-1）=6n+2.

（2）当n=12时，6n+2=6×12+2=74（根）；

（3）根据题意可得3m+20=6m+2，

解得m=6.

答（略）.

例8 如图，用火柴棒按以下方式搭“小鱼”.

1.搭1条“小鱼”需几根火柴棒？2条“小鱼”需几根火柴棒？3条“小鱼”需几根火柴棒？

2.照这样搭下去，搭n条“小鱼”，需要多少根火柴棒？

3.用少于50根火柴棒最多可以搭出来多少条“小鱼”？

【解析】1.搭1条“小鱼”需8根火柴棒，2条“小鱼”需14根火柴棒，3条“小鱼”需20根火柴棒.

2.照这样搭下去，搭n条“小鱼”，需要8+6（n-1）根火柴棒.

3.根据题意可得8+6（n-1）＜50，

解得n＜8.

∴最多可以搭出来7条“小鱼”.

【点评】用不等式解决问题的步骤：理解题意，找一个能表示实际问题意义的不等关系.在写解答的过程中，应先设未知数，再根据不等关系列出一元一次不等式，最后解这个不等式，写出答案.

方程与不等式是同属“数与代数”领域内的两部分内容，它们之间有密切的联系，存在许多可以进行类比的内容.我们在前面已经学习过有关方程（组）内容的基础上，充分发挥学习心理学中正向迁移的积极作用，借助已有的对方程的认识，可以为进一步学习不等式（组）提供一条合理的学习之路.

拓展训练

1.下列说法不一定成立的是（ ）.

A.若a＞b，则a+c＞b+c

B.若a+c＞b+c，则a＞b

C.若a＞b，则ac2＞bc2

D.若ac2＞bc2，则a＞b

答案：C.

2.2x-5＜5-2x的正整数解是 .

【解析】∵2x-5＜5-2x，

∴4x＜10，

∴原不等式的正整数解是1，2.

3.解不等式x+≤1-，并将解集在数轴上表示出来.

【解析】不等式的解集是x≤；

4.有10名菜农，每人可种甲种蔬菜3亩或乙种蔬菜2亩，已知甲种蔬菜每亩可收入0.5万元，乙种蔬菜每亩可收入0.8万元，要使总收入不低于15.6万元，则最多只能安排多少人种甲种蔬菜？

【解析】设安排x人种甲种蔬菜，则3x·0.5+0.8（10-x）·2≥15.6，x≤4.

故最多只能安排4人种甲种蔬菜.