基于改进状态空间进化算法的列车多目标优化

杜佳佳，李茂军，齐 战

（长沙理工大学电气与信息工程学院，湖南长沙410114）

1 引言

城轨列车自动运行（ATO）系统是列车运行速度控制的核心，列车运行的控制是一个需要同时满足安全、节能、准时、精确停车和舒适度多个目标的复杂的控制问题。列车运行过程的优化就是在列车的运行策略中寻找最优控制策略，在保证列车安全、节能、运行过程舒适的同时，能耗和运行时间达到铁路运营部门和乘客都可以接受的程度［1］。ATO系统在给定约束条件下寻找满足优化目标的速度-距离曲线，生成最优驾驶策略供下层控制参考，因此策略优化效果会对列车运行产生直接影响［2］。

Howlett基于庞特里亚金极大值原理证明在规定区间与时间内最小化列车运行能耗问题存在一个最优控制策略［3］。叶庆仕等确立了单列车区间运行优化模型与多列车节能运行模型并采用基于高斯白噪声扰动变异的粒子群算法（GMPSO）得出各情况下列车的最优控制策略［4］。余进等以列车能耗、运行时间及停靠准确性建立多目标优化模型，采用二进制和实数域的混合微粒群优化方法对列车运行控制序列和运行距离进行优化［5］。孟建军等采用遗传算法对高速列车ATO追溯目标曲线进行优化［6］。

针对传统进化算法存在有编程过程比较复杂、容易陷入局部最优等问题，本文研究设计了一种改进状态空间进化算法对城轨列车的运行过程进行优化，使列车能够满足节能、准时、停车精度及舒适度等指标。这种算法采用实数编码方式，构造一个状态进化矩阵来实现种群进化，并通过选种池中的选择操作实现优胜劣汰的自然选择机制，该算法相较于传统进化算法具有更强的搜索能力和更高的搜索精度，能够对列车进行更好的控制，其在收敛速度和收敛精度上有了大大的改善。

2 城轨列车运行的多目标模型

城轨列车在线路上运行时，列车驾驶员可以根据列车的实际运行速度、时间以及停车距离，选择适当的操纵方式对列车进行控制，前提条件是在保证列车安全、准时、准确停车的情况下，减少能耗。

城轨列车ATO系统是一个复杂的非线性系统，该系统存在多个输入、输出变量，以城轨列车运行时的能耗、精确停车、准时性和舒适性等性能指标为目标，同时以列车动力学方程作为约束，建立多目标模型，并对列车的能量消耗模型、舒适性模型、停车精度模型和准时性模型分别进行描述［7］。

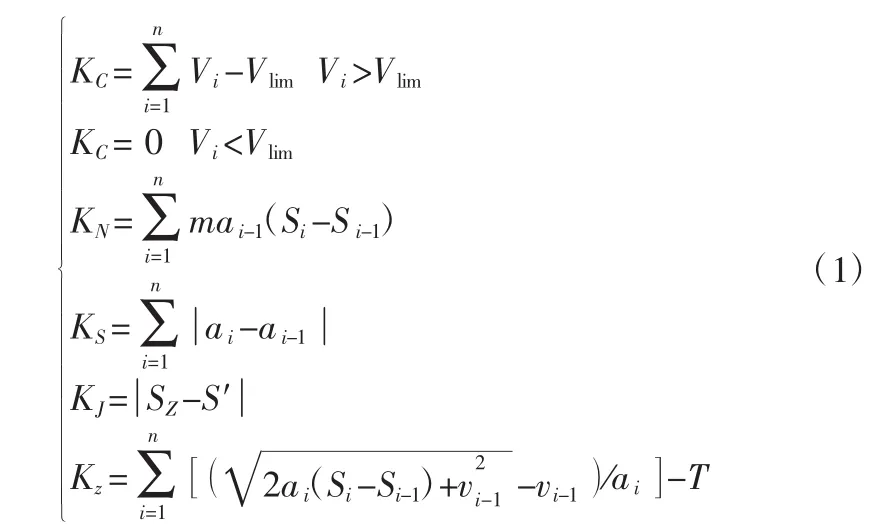
其中：KC指列车速度防护指标，Vi指第i个工况转换点的列车运行速度，V限指运行线路各个阶段的限速。KC越小表示列车在运行过程中出现超速情况越小，列车运行越安全。KN为列车能量消耗指标；ai为第i个工况的加速度；Si为第i个工况的位移。KS为舒适度衡量指标；ai为工况点的加速度。KS越小，列车舒适度越好。因此，在列车自动运行速度曲线优化中应该保证舒适度衡量指标KS越小越好。精确停车指标模型就是列车在整个运行过程中走行的距离与列车从运行起点到停车点之间的距离差，停车点的停车误差应在±25cm范围内［8］。KJ为停车精度误差衡量指标；SZ为列车的实际行驶距离；S′为两个车站间的距离。T为列车在两站间规定的运行时间，列车的实际运行时间与规定的时间误差≤5%。

状态空间模型进化算法本质上是无约束条件的算法，所以把约束条件当做目标函数来建立模型。综上所述，以节能、精确停车、准时和舒适性等为目标的多目标优化问题模型为：

式中：min表示取函数的最小值，即各个子目标函数都尽可能的取最小值。

对于多目标优化问题的求解，将采用加权和方法将其聚合为单目标优化问题并通过状态空间模型进化算法来进行求解。

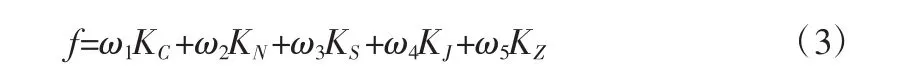
其中：ω1，ω2，ω3，ω4和 ω5为权重系数，满足 ω1＋ω2＋ω3＋ω4＋ω5＝1。则多目标问题转换为下式所示的单目标优化问题：

3 改进状态空间进化算法

改进状态空间进化算法是基于离散系统的状态空间模型，采用实数编码方式，引入了遗传算法思想的寻优算法［9］。考虑离散系统状态空间模型：

其中，X（k）表示第k代群体，包含N个个体，每个个体包含M个变量，即X（k）是一个N×M的矩阵。G表示状态进化矩阵，是一个N×N的矩阵。

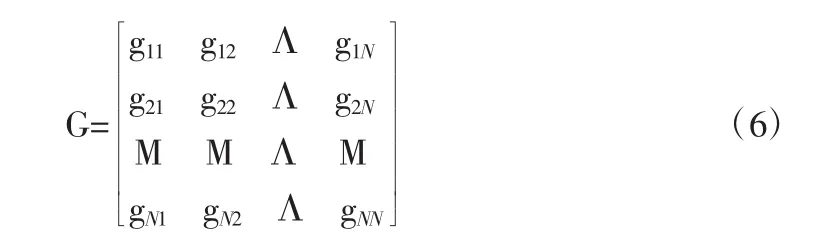
其中，0＜gij≤b/（a×N），i，j＝1，2，L，N。矩阵G是一个各元素取值相互独立的随即矩阵，其中［a，b］为种群内个体元素的取值范围。G 矩阵按照式（2）构造时，算法是收敛的［10］。同传统进化算法类似，按照优胜劣汰的进化思想，选择操作从选种池中选择适应度函数值高的个体作为下一次进化的初始种群。每次进化完成后将种群X（k）和经过状态进化矩阵G作用后生成的新种群X（k＋1）一起放入这个选种池。在处理无约束最小化优化问题时，直接按照适应度函数f（g）计算出选种池中每个个体的适应度值Y（k），并将Y（k）从小到大排列，选择Y（k）中前N个元素对应的个体组成新一代种群X′（k＋1），经过选种池的作用，再随机选择一些适应度较差的个体再编码定义域内的任意值，和适应度优的个体组成新的群体接着向下一代进化。在处理约束最小化问题时，只需分别对初始种群X（k）和进化完成后得到的新种群X（k＋1）进行相应处理，使其满足约束条件，因此本算法较传统进化算法处理约束条件显得更加灵活。

4 仿真结果与分析

论文选择对研究列车运行控制有影响的运行环境参数，包含了线路长度和线路限速信息，假定具体运行环境参数如表1所示。

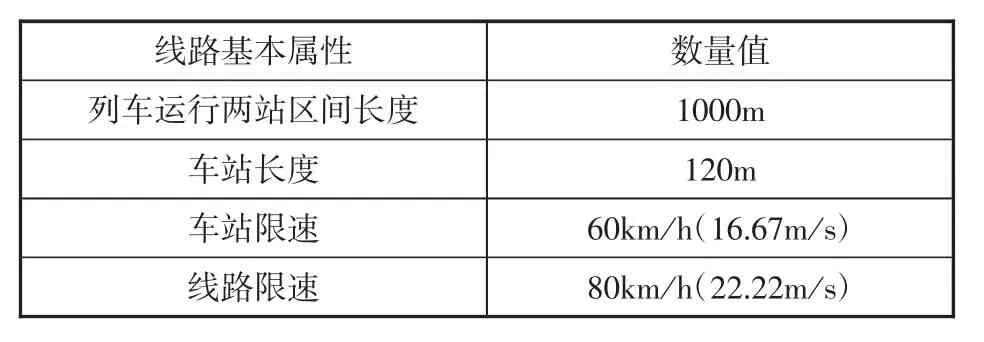
表1 列车运行环境参数

假定列车属性参数如表2所示。

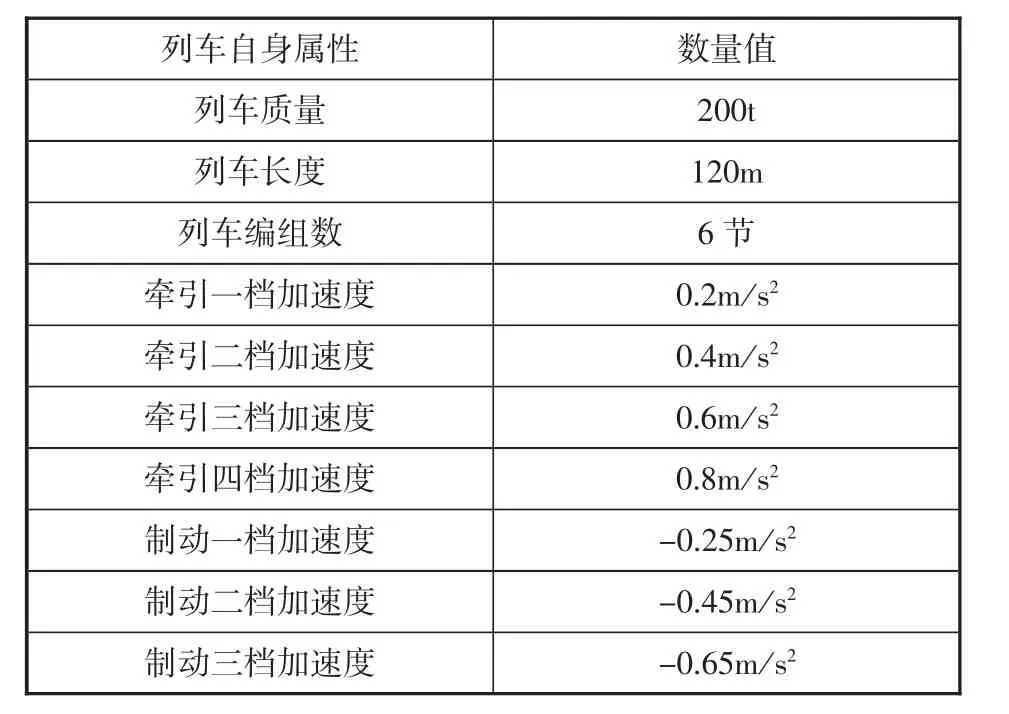
表2 列车自身属性参数

为了验证状态空间模型进化算法对于优化列车速度的可行性，论文采用Matlab进行计算机仿真，验证列车自动运行速度曲线。根据前面的线路数据和列车自身属性的数据，在调整权重的时候，需要根据自身数量级和对于控制效果的影响程度进行调整。文献［11］对各项性能在各个阶段的影响程度进行了研究，而后运用层次分析的思想确定了层次结构，然后结合利用熵值法确定的客观权重和层次分析法确定的主观权重，得到了AHP-Entropy的综合确权的方法。最后，定量确定各项性能指标的权重大小，为基于状态空间模型进化算法列车自动运行速度曲线的优化中群体适应度函数的计算奠定基础［11］。因此，论文取 ω1＝0.49，ω2＝0.01，ω3＝0.03，ω4＝0.20，ω5＝0.27。

列车在计算时，选取某城轨列车线路上运行距离为1000m的一个站进行仿真计算，列车在该段线路上运行规定时间为90s。使用状态空间模型进化算法进行计算时，种群大小为1000，最大种群代数200。在MATLAB环境下，根据牵引-匀速-制动控制策略来进行运行。列车运行过程中，选择工况的个数为10，因为线路的长度为1000m，所以选择10个工况可以完成整个线路的控制过程。

用改进状态空间进化算法进行求解，得到列车的距离-速度曲线如图1所示。

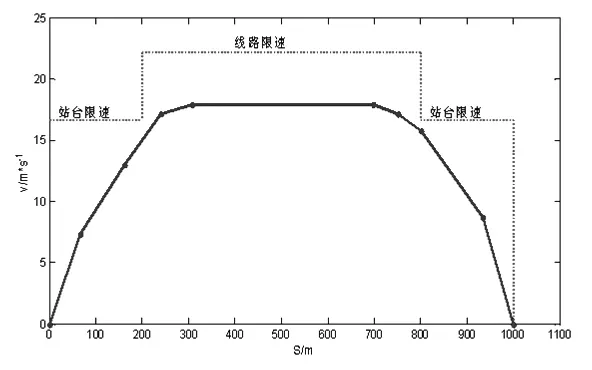
图1 改进进化算法的距离-速度曲线

仿真得到 10 个工况点 （S，a） 的具体数据为（0，0.4）（66.67，0.6）（147.87，0.8）（226.70，0.2）（293.37，0）（720.09，-0.25） （770.96，-0.45） （818.67，-0.65） （939.56，-0.65）（1000，-0.65）。

通过对目标曲线的30次仿真优化取其平均值，仿真结果见表3。

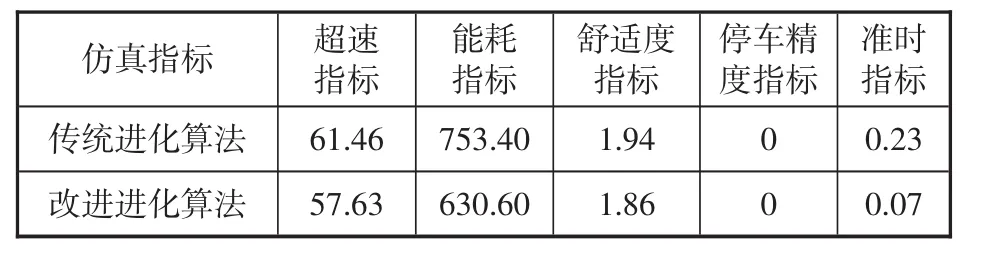
表3 列车自动运行优化仿真结果

从表3可以看出改进的算法各项指标结果的优化程度较传统算法还是比较明显的。经过改进算法后，速度防护指标的适应度由 61.46 优化到 57.63，降低了 6.2%；能耗指标的适应度由753.40 优化到 630.60，降低了 16.3%；舒适度指标的适应度由1.94优化到1.86，降低了4%；准时指标的适应度由 0.23 优化到0.07，降低了70%，即准时性指标也得到了很大程度的优化。通过仿真结果分析，当种群为1000，最大代数为200时列车自动运行的速度防护指标，准时性指标，停车精度指标，舒适性指标，节能性指标都同时满足要求并得到了极佳的优化。

传统状态空间模型进化算法和改进进化算法进化代数结果如图2所示。

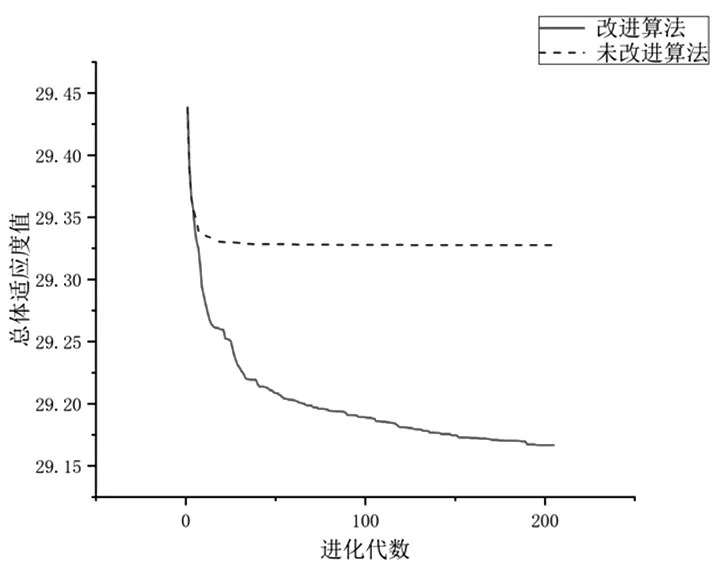
图2 传统与改进进化算法的进化代数

从上图图形曲线可以看出，传统的进化算法对初始群体进行19次进化迭代后，曲线走势趋于平缓，此时对应的纵坐标值即为所求的最优函数值。而改进进化算法为183代，虽然传统进化算法的进化代数比改进进化算法收敛速度更加快速，只需要在极少的迭代次数后就可以找到全局最优解，但是总体适应度值更大，搜索结果没有改进算法的精确。

因此，通过牵引-匀速-制动的控制策略能够使列车充分利用区间进行运行，使用状态空间模型进化算法对城轨列车运行过程优化后，可使列车在运行过程中达到最优或者次优，满足列车准时、精确停车、舒适和节能等要求，能够获得满意的结果。从而也看出了状态空间模型进化算法可以在较少的迭代次数下获得最优函数值，验证了改进进化算法在优化城轨列车ATO多目标控制策略中的可行性和优越性。

5 结束语

针对列车运行多目标优化的特点，本文采用了加权求和的方法将多目标问题转换为了单目标问题的求解并且提出了一种改进状态空间进化算法。通过对初始种群的再处理实现种群持优化，设计了ATO速度优化仿真系统，借助于MATLAB平台得到列车运行理想目标曲线，对算例进行分析并用传统进化算法和改进进化算法来做仿真实验，得出仿真结果。经过两种算法数据分析对比，验证了改进算法在优化城轨列车ATO多目标控制策略中的可行性和优越性。