《1.2.2空间中的平行关系－平面与平面平行（二）》教学设计

辽宁省抚顺市德才高级中学 刘 爽

学习目标：

1.会用图形语言、符号语言表示面面平行的性质定理

2.记住空间中面面平行的性质定理

3.应用定理证明相关问题

重点：

平面与平面平行的性质定理。

难点：

平面与平面平行性质定理的应用。

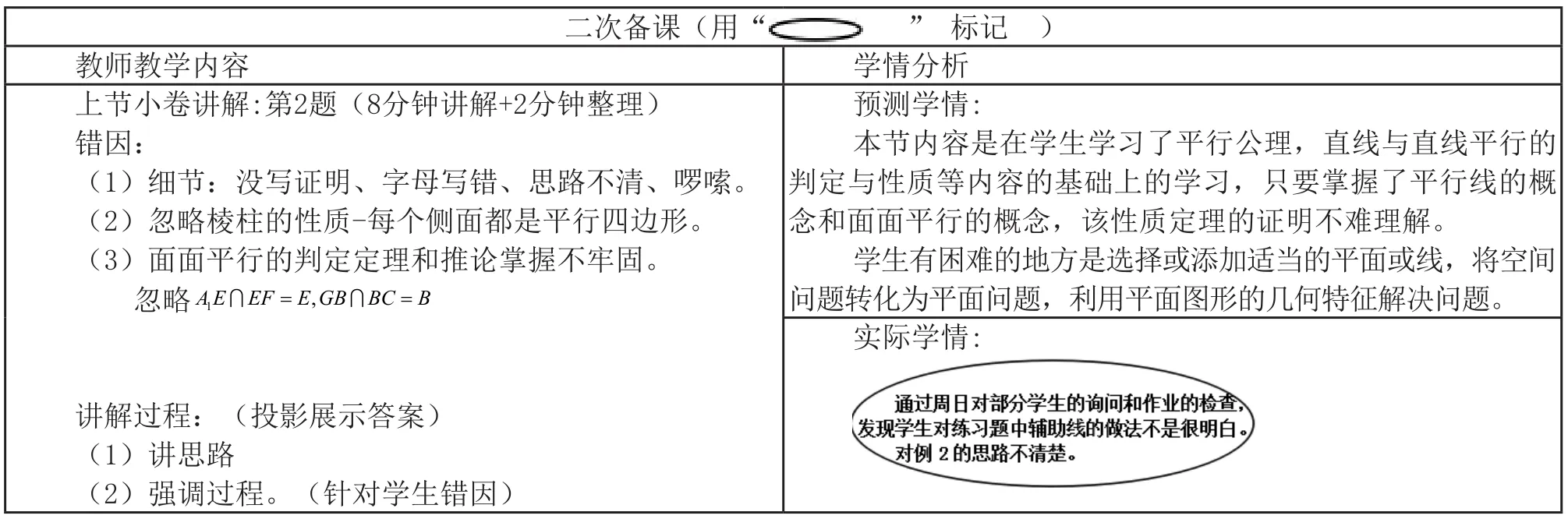
二次备课（用“” 标记 ）教师教学内容 学情分析上节小卷讲解:第2题（8分钟讲解+2分钟整理）错因：（1）细节：没写证明、字母写错、思路不清、啰嗦。（2）忽略棱柱的性质-每个侧面都是平行四边形。（3）面面平行的判定定理和推论掌握不牢固。忽略AE EF E GB BC B 1∩=,∩=预测学情:本节内容是在学生学习了平行公理，直线与直线平行的判定与性质等内容的基础上的学习，只要掌握了平行线的概念和面面平行的概念，该性质定理的证明不难理解。学生有困难的地方是选择或添加适当的平面或线，将空间问题转化为平面问题，利用平面图形的几何特征解决问题。实际学情:讲解过程：（投影展示答案）（1）讲思路（2）强调过程。（针对学生错因）

教学环节教师教学内容 学生活动、问题设置一、创设情景、导入新课(2分钟)问题探究：思考1.如果两个平面平行，那么一个平面内的直线与另一个平面的位置关系如何？思考2.观察长方体的教室，天花板面与地面的位置关系是怎样的？直观感觉上，墙面分别与天花板面、地面相交所得到的两条交线有怎样的位置关系?【师】我们把这样的关系用图形表示如下。生】平行【生】平行【生】观察 齐答：平行二、新课新知（6分钟）面面平行的性质定理文字语言 如果两个平行平面同时与第三个平面相交，那么它们的交线平行.图形语言问题1、a，b分别在两个平行平面内 ，它们有没有公共点？生】没有.问题2、a，b都在平面r内吗？【生】在.问题3、直线a，b的位置关系是什么？【生】平行问题4、谁能尝试归纳一下什么是面面平行的性质定理？思考 学生代表回答问题5、面面平行性质定理的符号语言是？问题6、面面平行性质定理用来解决什么问题的?【生】思考齐答：用面面平行来证明线线平行α，β符号语言【师】这就是面面平行的性质定理。【师】那么面面平行的性质定理怎么应用呢？我们一起来看例1.例1.已知：如图， 外的一点，直线PAB，PCD分别与α β//，点P是平面α，β相交于点A,B和C,D：(1)求证：α，β AC BD //；(2)已知，PA cm=4，AB cm=5，PC cm=3求PD的长.

证明：（1）因为α β//又因为 平面PBD AC=∩á（6分钟）平面PBD BD=∩â所以AC BD //(2) 因为AC//BD问题7、初中学习的平行线截得的线段有什么样的规律？【生】思考学生代表回答：两条平行线截对应线段成比例。所以PA PC PB PD=所以PD=27 4cm练习：已知,平面α∥平面β∥平面γ，两条直线l，m分别与平面α，β，γ相交于A,B,C.点和点D,E,F,求证：=（8分钟）AB DE BC EF证明： 连接DC，与平面β相交于点G，则平面FCD与平面β，分l别相交于直线GE，CF.因为α∥β,β∥γ所以 BG //AD，GE //CF.因此问题8、两条直线l，m一定共面吗？【生】不一定.问题9、能不能连接A，D和B，E，来证明AD//BE？为什么？【生】不能.因为AD与BE可能是异面直线.问题10、连接D，C后，除平面α,β,γ外，图中还有哪几个平面？进一步分析如何应用平面与平面平行的性质定理.所以问题11、通过本题，我们能得出什么结论？