波利亚的解题理论的实践解读

上海市徐汇区教育学院附属实验中学 伊金凤

“怎样解题表“讲的是“怎样解题”“怎样学会解题”的问题，并按照解决问题时思维的自然过程分成四个阶段—— 弄清问题、拟定计划、实现计划、回顾，描绘出解题理论的一个总体轮廓，组成了一个完整的解题教学系统。它集解题步骤、解题策略、解题方法于一身，融理论与实践于一体。

下面结合示例来解读波利亚的解题表。

弄清问题“是认识问题，并对问题进行表明的过程，应成为成功解决问题的一个必要前提。

例 如图：已知△ABC，AD平分∠BAC，F为AD中点，过点F作AD的垂线，交AB于点G，交AC于点H，交BC延长线于点E，求证：DE2=BE·CE.

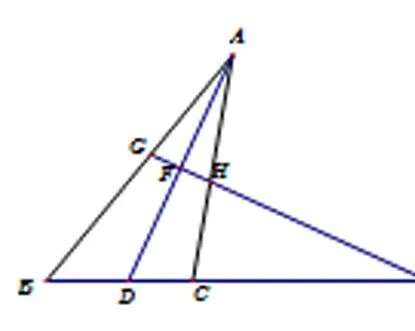
一、弄清问题

在教学中，我们要帮助学生弄清问题，可以先设计几个有启发性的问题。比如：问题1：你要求解的是什么？（先明确目标）要求解的是证明一个等积式，即DE2=BE·CE.问题2：你有些什么？

学生的回答可能是杂乱的、无序的、想到什么就说什么的等，要想让学生的回答相对完整、思维有序，这就要求我们教师在平时的教学中要有意识地进行引导。回答这个问题，可以从以下三个方面思考：

(1)已知量是什么？（用最精练的语言概括）（如：AD平分∠BAC，EG垂直平分AD）

(2)与本题相关的定义、定理、公式、法则等。（角平分线的性质、线段垂直平分线的性质）

(3)已有的解题经验是什么。（是否解决过类似的问题？）我们的解题经验是：等积式可以转化成比例式；证比例式，可以考虑证相似或比例线段。

二、拟定计划

在整个解题表中”拟定计划“是关键环节和核心内容。“拟定计划“的过程是探索解题思路的发现过程，也是一个化归过程，波利亚的建议是分两步走：第一，努力在已知与未知之间找出直接的联系（模式识别），这是最简单的直接化归；第二，如果找不出直接的联系，就对原来的问题做出某些必要的变更或修改，引进辅助的问题等，这是最实质的曲折化归。为此，在”怎样解题表“中，波利亚拟出了启发、引导我们不断转换问题的30多个问句或建议：把问题转化为一个等价的问题，去考虑一个可能相关的问题，先解决一个更特殊的问题、或更一般的问题、或类似的问题，等等。都是在启发化归的念头，都是在提示化归的途径。这实际上是阐述和应用化归策略，并进行资源的提取与分配。

根据波利亚的怎样解题表，我们的任务就是将未知量与已知量联系起来。

问题3：怎样才能求得DE2=BE·CE？

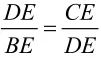
问题4：替换什么？如何进行替换？

我们可以替换线段，也可能替换比式。先考虑替换线段。观察图形，我们会想到线段垂直平分线的性质，于是，联结AE，则AE=AD.用线段AE替换要证结论中的AD，则我们的目标式变为了：.我们观察新的比例式中的四条线段（“横看”或“竖看”），用“三点定形”法，从而可证△ABE∽△CAE.

问题5：如何证△ABE∽△CAE？

这是一典型的基本图形，两个三角形有一个公共角（∠AEB=∠CEA），结论让我们证明两边成比例，所以我们需要再证明一对对应角相等，比如想证：∠ABE=∠CAE.

问题6：如何证∠ABE=∠CAE?

通过全等？等边对等角？相似？我们会在心中快速地搜索可行方案，同时结合已知条件及图形结构特征，我们会排除全等、相似等方法。

这时，我们可能会回到原图，进一步搜索可以利用的条件和信息。我们有可能发现∠EDA=∠EAD，即∠B+∠DAB=∠CAE+∠CAD，从而∠ABE=∠CAE.

至此，我们已经在结论与已知量之间建立起了一个不中断的联络网，解题思路全部沟通。

三、实现计划

这四个阶段中“实现计划“虽为主体工作，但较为容易，是思路打通之后具体实施信息资源的逻辑配置，“我们所需要的只是耐心”。

联结AE.

由线段垂直平分线的性质，得AE+DE

∴∠EDA=∠EAD

即∠B+∠DAB∠CAE+∠CAD

又AD平分∠BAC，得∠DAB=∠CAD

∴ ∠ABE=∠CAE，又∠AEB=∠CAE

∴△ABE∽△CAE

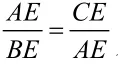
四、回顾

回顾“是最容易被忽视的阶段，波利亚将其作为解题的必要环节而固定下来，是一个有远见的做法。

第一，正面检验每一步，推理是有效的。

第二，“你能否用别的方法导出这个结果？”在信念上我们应该永远而坚定地作出肯定的回答，操作上还未实现只是能力问题或暂时现象。对于本例，按照替换比式想法，可以有下面的解法。

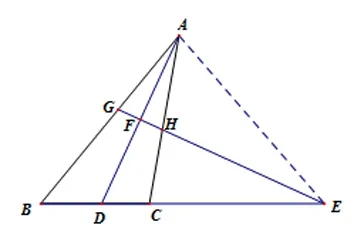
再次观察图形结构，注意到AD平分∠GAH，且AF⊥GH这个局部图形。因此就会作出GF=FH的判断。于是AD与GH互相垂直平分，所以如果联结DG、DH，则四边形形AGDH是菱形。

这样我们就不难得到DH∥AB且DG∥AC，而平行线会推出比例式。

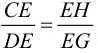
从而得证。

第三，你能不能把这一结果或方法用于其他问题？“能，我们可以把证明线段成比例的思考流程总结如下：

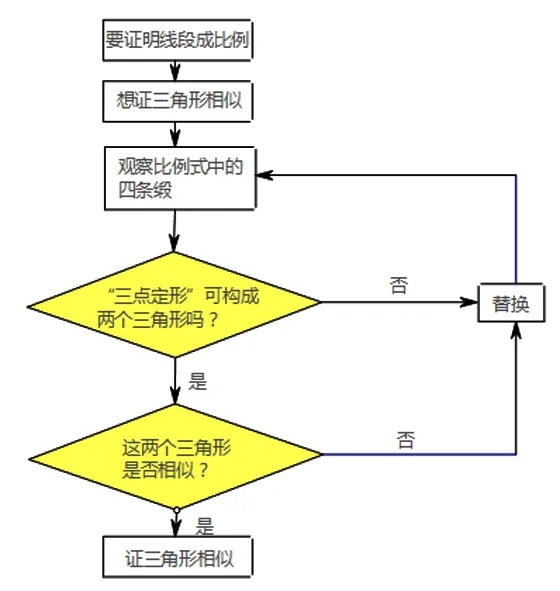
这个学习过程不是单纯地解题，而是通过解题获得新知识和技能的学习过程，我们的目标不是找出可以机械地用于解决一切问题的“万能方法”，而是通过对于解题过程的深入分析，特别是由已有的成功实践，总结出一般的方法或模式，使得在以后的解题中可以起到启发的作用，学生的推理能力也在潜移默化中得到了提升。

波利亚的这张表是他提出的数学教学要“教思考”的一个典范。前后联系的逐步深入的所有问句正是条理化、概括化的思维活动的科学表达。

“怎样解题表”讲的是“怎样解题”、“怎样学会解题”的问题，按照解决问题时思维的自然过程分成四个阶段——弄清问题、拟定计划、实现计划、回顾，描绘出解题理论的一个总体轮廓，组成了一个完整的解题教学系统。它集解题步骤、解题策略、解题方法等于一身，融理论与实践于一体。

这4个步骤需要不断地反馈调节，即4个步骤完成了也存在反思改进的空间：有时候思路还比较麻烦，通过反馈调节而精简；有时候思路还存在错误，通过反馈调节而纠正。