桁架主梁桥梁颤振流固耦合数值仿真计算*

詹 昊 郭子会 闫斗平 廖海黎

(1.西南交通大学土木工程学院 成都 610031； 2.内蒙古伊泰准东铁路有限责任公司 鄂尔多斯 010300；3.郧县锦宏路桥工程有限责任公司 十堰 442500； 4.中铁大桥勘测设计院集团有限公司 武汉 430056)

颤振是一种空气动力失稳现象，会引起灾难性的后果。桥梁结构一般为非流线型断面，当气流流经时会发生涡旋和流动分离，形成复杂的空气作用力，当空气力受结构振动的影响较大时，同振动结构形成一个相互作用反馈机制，动力系统的空气主要表现为一种自激力。当桥梁结构与产生自激气动力的绕流气流形成振动系统阻尼在不断的相互反馈作用中由正值变为负值时，振动系统吸收的能量超越了自身耗能能力而造成系统振动发散，这种空气动力失稳现象就是桥梁颤振。塔科玛海峡桥风毁就是由颤振所引起。

随着桥梁跨度的增加，其结构对风的敏感性也逐渐增加，因此，颤振稳定性往往是桥梁设计中首要考虑的因素。桁架主梁桥梁广泛运用于公铁两用大桥、双层公路桥梁和山区桥梁。对于基于流固耦合理论的颤振计算，国内外学者作了比较深入的研究，但由于桁架主梁构造复杂，一般简化为平面模型计算。文献[1-2]将钢箱主梁简化为平面模型，运用离散涡方法进行颤振计算，文献[3]将钢箱主梁简化为平面模型，运用有限元方法进行颤振计算，文献[4]将钢桁主梁简化为平面模型，运用无网格涡方法进行主梁静力三分力系数计算，文献[5]将桁架主梁简化为平面模型，运用有限体积法计算主梁颤振导数，文献[6-7]通过风洞实验研究桁架主梁桥梁颤振稳定性。

黄冈长江大桥为主跨566 m的双塔双索面斜拉桥，主跨跨度、主桁杆件倾斜度、斜拉索破断力和抗压、抗拉支座均居世界已建成桥梁之首。黄冈公铁两用长江大桥效果图见图1，横断面图见图2。

图1 黄冈公铁两用长江大桥效果图

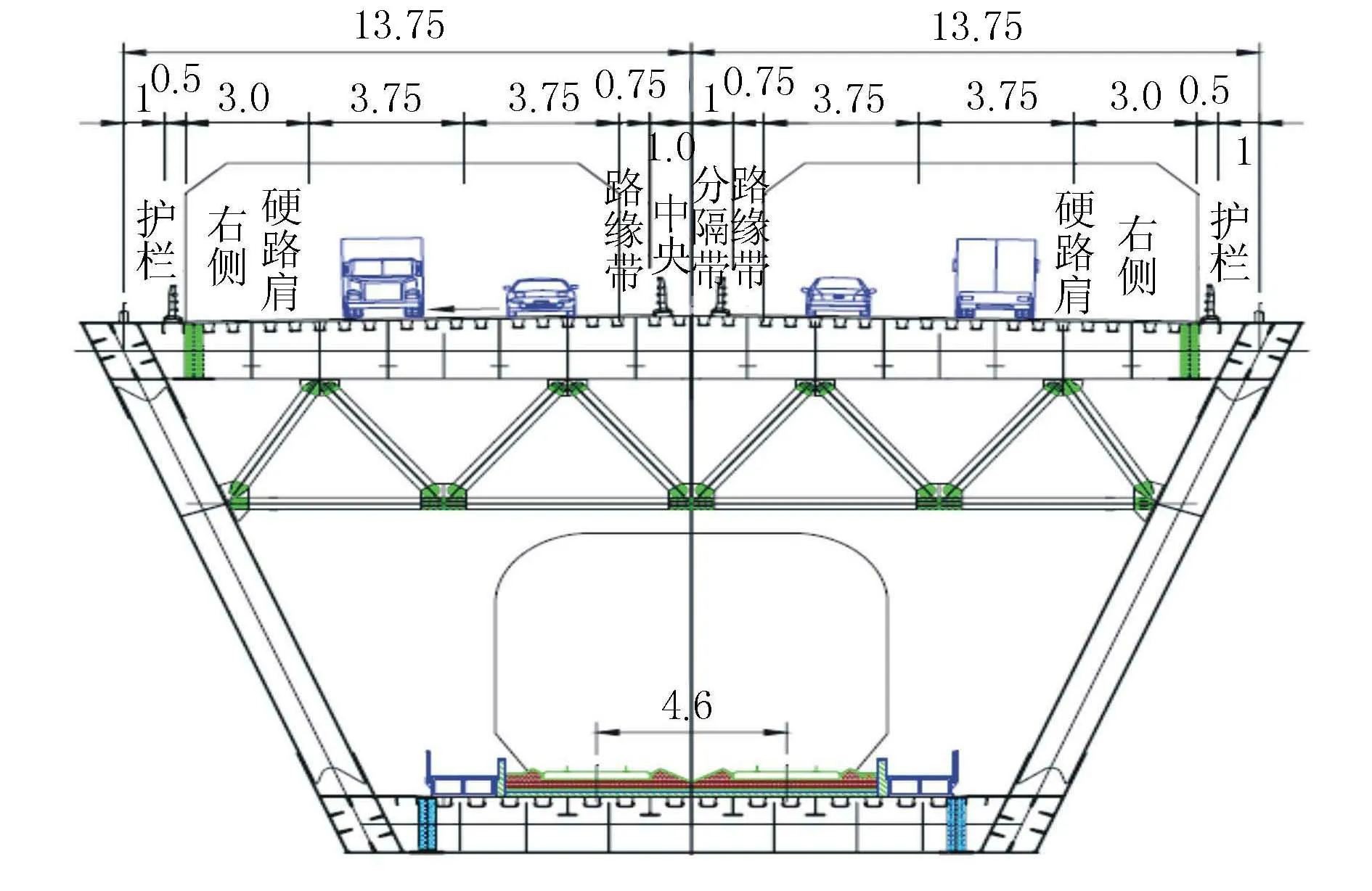
图2 黄冈公铁两用长江大桥横断面布置图(单位：m)

本文通过对FLUENT二次开发，建立了基于几何三维的竖弯和扭转流固耦合数值仿真计算模型，对黄冈长江大桥进行了颤振数值仿真计算，并与节段模型风洞试验结果进行了比较。建立桁架主梁三维模型，运用流固耦合方法计算颤振临界风速，国内外还未见相关文献报道。该桥颤振检验风速为60.4 m/s，设计要求颤振临界风速大于颤振检验风速。

1 数值仿真计算原理

将主梁作为质量、弹簧和阻尼系统，如图3所示。研究对象为刚体，假设物体沿展向的竖向位移和扭转位移相同。竖向振动方程和扭转振动方程如式(1)和式(2)所示。

(1)

(2)

式中：m为单位长度的质量；Iθ为惯性矩；kh为竖向刚度；kθ为扭转刚度；ch和cθ分别为结构竖弯阻尼和扭转阻尼；Fh和Mθ为流体力；y为结构竖向位移；θ为扭转角度。对于不可压缩流体的连续方程和纳维-斯脱克斯方程如式(3)和式(4)所示，梯度算子如式(5)所示。

U=0

(3)

Ut+(U·p+υ2U

(4)

(5)

流体质点速度向量U={u，υ，w}T；X，Y，Z为笛卡尔坐标系；ρ为流体密度，i，j，k为单位向量。假设空气的密度ρ=1.225 kg/m3,气温20 ℃时，运动黏度υ为1.5×10-5m2/s。求解方程(3)、(4)，得到主梁周边的压力场和速度场，计算作用在主梁上的气动力，这可以通过FLUENT直接完成。然后提取升力和力矩赋值给振动方程(1)、(2)，运用Newmark方法求解主梁振动方程。再将速度传给主梁，通过FLUENT的动网格技术使主梁运动。然后开始下一步的流固耦合循环计算。以上流固耦合计算过程通过对FLUENT 二次开发完成。竖弯振动方程的Newmark方法的算法如下[9]。

1) 计算刚度k，质量m和阻尼矩c。

2.2.2 有效穗。考察结果详见表5，分析可知施用磷肥的小麦有效穗平均为45.1万/亩，比未施用磷肥处理有效穗39万多6.1万/亩，施用磷肥增加了小麦的有效穗。

3) 选择步长Δt，参数γ和β，并计算下列有关参数。

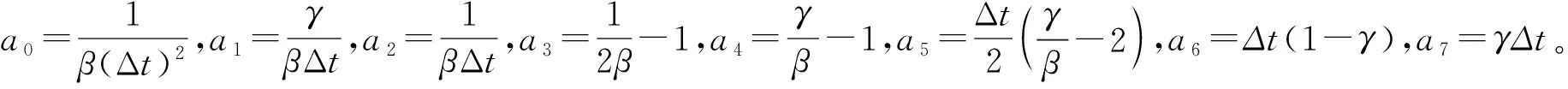
4) 形成刚度

对于每个时间步长的计算步骤如下。

①计算t+Δt时刻的荷载

③计算t+Δt时刻的加速度、速度

同理可求扭转振动方程的解。

2 数值仿真计算模型

数值仿真计算模拟节段模型风洞实验，但按照实际桥梁尺寸建模，克服了节段风洞实验模型由于缩小尺寸而带来的雷诺数效应误差，主梁取56 m长的节间。计算参数如表1所示[9]，以最不利的第一阶正对称竖弯和第一阶正对称扭转模态组合计算，结构阻尼比取0.005，节段风洞试验模型见图4。

表1 计算参数

图4 节段风洞试验模型

数值仿真计算模型见图5，数值仿真计算区域见图6，长宽高分别为420 m、72 m和370 m。计算网格划分见图7。

图5 数值计算模型

图6 数值计算区域

图7 数值计算网格

如图7所示，风向从左至右，左侧设定为速度入口，右侧设定为自由出流。上下边界为无滑移固壁边界，数值计算中，靠近主梁网格加密,远离主梁网格逐渐稀疏。网格总数约100万，采用有限体积法求解，其中对流项采用中心差分格式，压力和速度的耦合采用SMPLEC算法，计算采用LES湍流模型，时间步长取0.005 s。由于流固耦合计算费时，再加上网格数量大，因此本文采用了并行计算技术，运用多核工作站进行计算。

3 数值仿真计算

旋涡脱落图见图8。

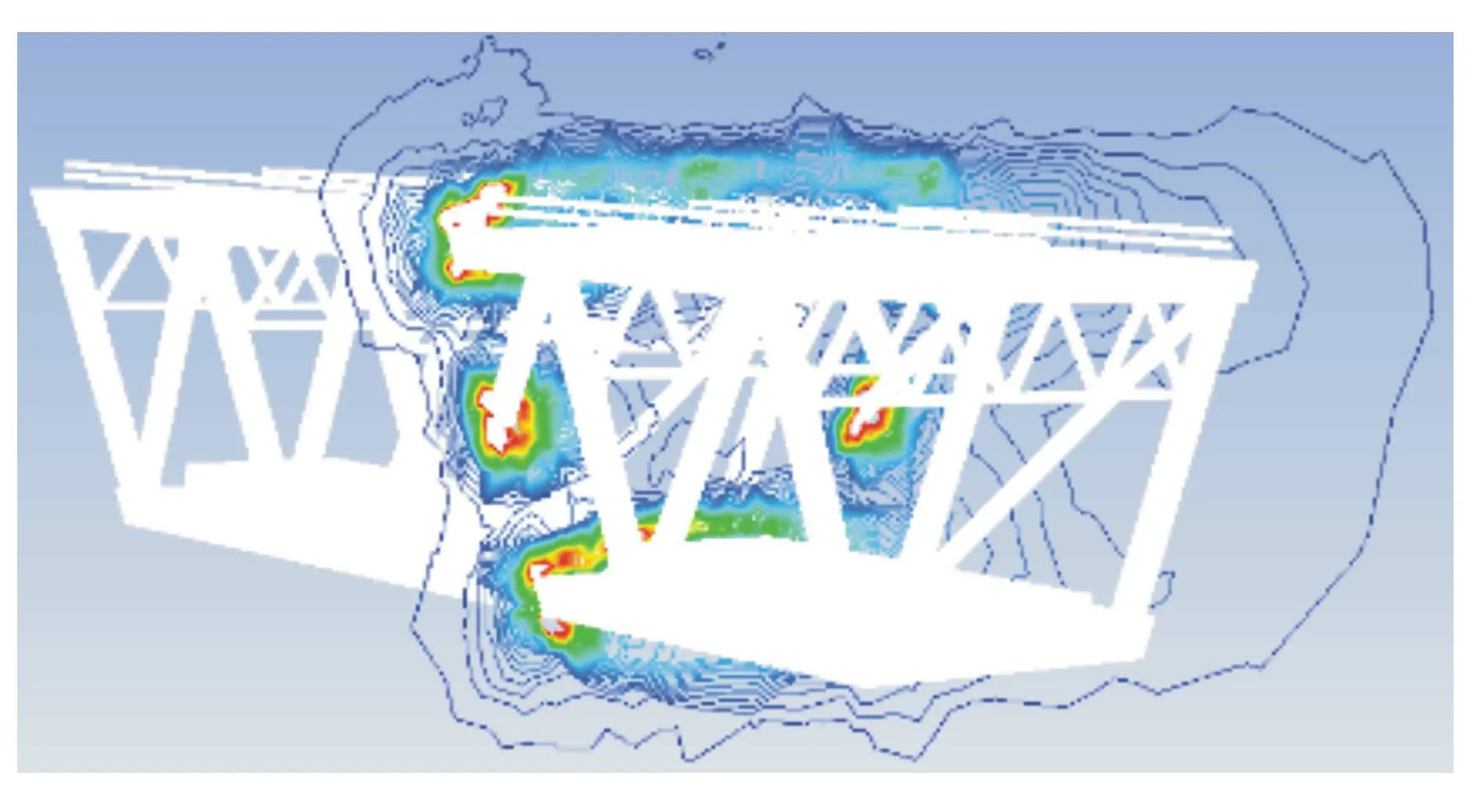
图8 旋涡脱落图

由图8可知，桁架主梁构造复杂，由于弦杆的存在，旋涡脱落表现为复杂的形态，若简化为平面模型计算，将与实际结构存在较大差别。0°风攻角时，主梁位移时程曲线见图9、图10。

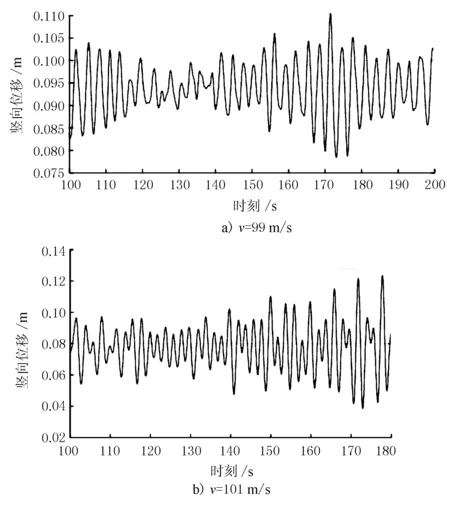
图9 主梁竖向位移时程曲线(0°风攻角)

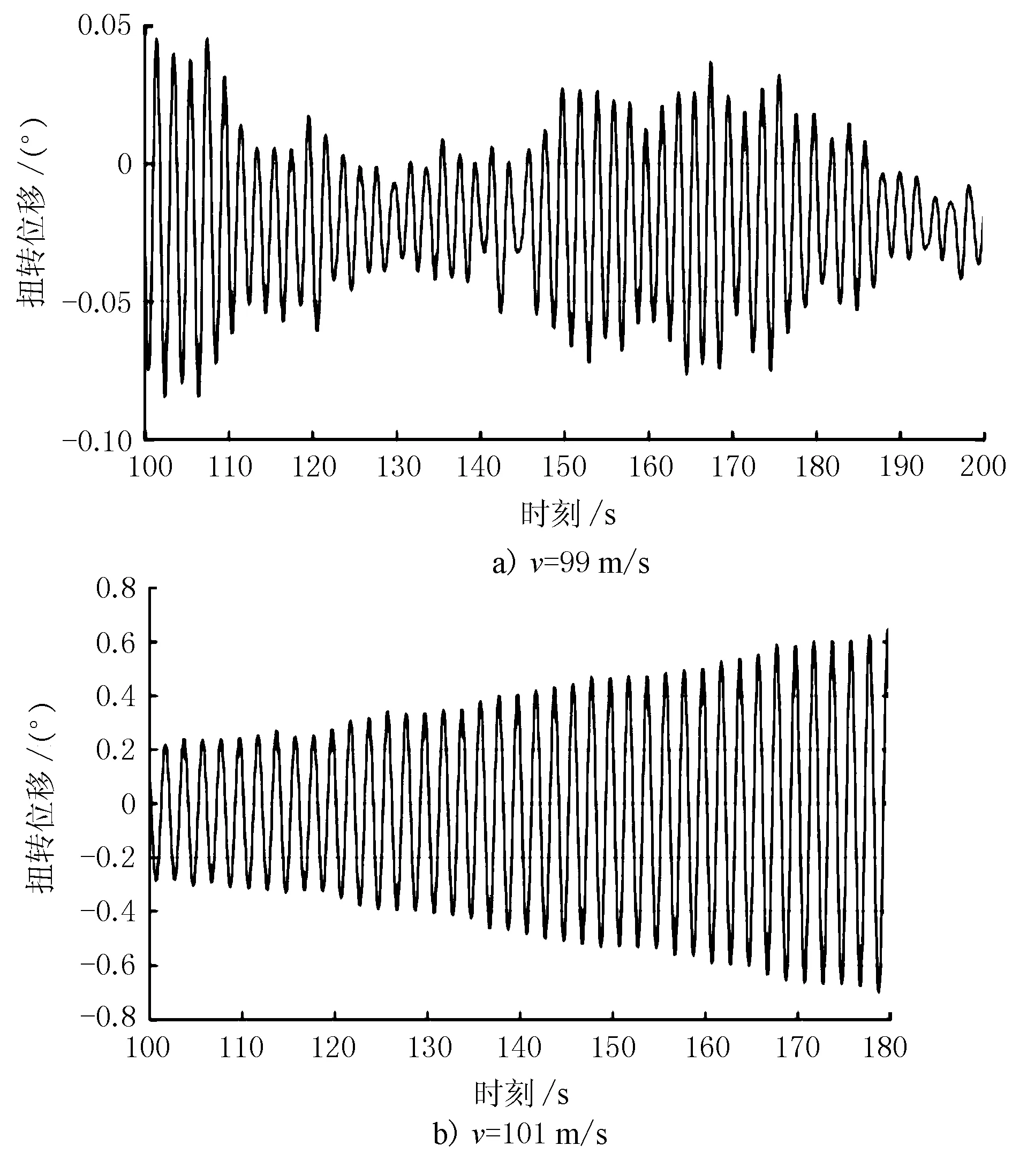
图10 主梁扭转位移时程曲线(0°风攻角)

由图9和图10可见，当风速为99 m/s时，主梁竖向位移幅值和扭转位移幅值基本保持恒定；当风速为101 m/s时，主梁竖向位移幅值和扭转位移幅值随时间逐渐增大，呈现发散振动的趋势。以开始发散振动时的风速作为颤振临界风速，可知0°风攻角时，颤振临界风速为99～101 m/s。同理可以计算得到+3°风攻角时，颤振临界风速为78～80 m/s，颤振临界风速见表2。

表2 颤振临界风速

由表2可知，数值仿真计算值和节段模型风洞实验值基本吻合，颤振临界风速大于颤振检验风速60.4 m/s,满足颤振稳定性要求。

4 结论

1) 桁架主梁构造复杂，由于弦杆的存在，旋涡脱落表现为复杂的形态，若简化为平面模型，将与实际结构存在较大差别，难以反映真实的流场情况。

2) 本文数值仿真计算结果和风洞试验结果基本吻合，说明了方法的有效性和准确性。本文模拟节段模型风洞实验，同时可以按照实际桥梁建模，能够克服节段风洞实验模型由于缩小尺寸而带来的雷诺数效应误差。

3) 本方法可以建立结构的三维几何模型进行抗风计算，适用于任何桥梁主梁结构，为桥梁结构抗风计算提供了新的思路。

[1] LARSEN A，WALTHER J H. Aeroelastic analysis of bridge girder sections based on discrete vortex simulations[J].Journal of Wind Engineering and Industrial Aerodynamic，1997，67/68：253-265.

[2] LARSEN.Advances in aeroelastic analyses of suspension and cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics，1998,74：73-90.

[3] FRANDSEN J B. Numerical bridge deck studies using finite elements.Part I:flutter[J].Journal of Fluids and Structures,2004,19(2):171-191.

[4] MOLHOLM M, JOHANNES H, RASMUSEN J T, LARSEN A, et al.On estimating the aerodynamic admittance of bridge sections by a mesh-free vortex method [J].Journal of Wind Engineering and Industrial Aerodynamics,2015,146:117-127.

[5] 陈艾荣，艾辉林.计算桥梁空气动力学：大涡模拟[M]北京：人民交通出版社，2010.

[6] 白桦，李宇，李加武，等.钢桁架悬索桥颤振稳定性能研究[J].振动与冲击，2013(4):90-95.

[7] 邓育林,郭庆康,何雄君,等.考虑流固耦合作用的桥梁深水矩形空心高墩振动特性分析[J].武汉理工大学学报(交通科学与工程版),2016,40(6):968-972.

[8] 刘庆宽，盛永青，马文勇，等.小宽高比钢桁架悬索桥颤振稳定气动措施的试验研究[J].实验流体力学，2012(3)：26-30.

[9] 王元汉，李丽娟，李银平.有限元法基础与程序设计[M].广州:华南理工大学出版社，2002.