抗非视距的室内三维定位方法

, , ,

(成都信息工程大学 通信工程学院,四川 成都 610203)

近年来,随着社会的不断进步和科技的快速发展,人们对室内无线定位服务的精度要求日益增加。对未知对象位置的预测广泛应用于公共场合用户定位及物流公司货物位置定位等领域。然而,传统的定位技术应用到室内环境时,由于室内存在各种阻碍物,因此出现了多径效应[1]。如何解决非视距(NLOS)环境影响和多径效应成为提高室内定位精度的关键[2],也是当前研究的重点。

目前常用的定位方法有:泰勒级数展开法、Chan算法、Fang算法、LS算法、到达时间差算法(TDOA)/角度定位算法(AOA)[3]等。TDOA/到达时间(TOA)[4-5]定位方法只需要接收机中时间同步的精确,而不是接收机和发射机之间的绝对时间同步,因此时钟精度容易实现。此外,与其他定位方法相比,该方法可以更好地适应复杂的室内环境并提供更高的定位精度[6]。

小波阈值去噪方法[7]不仅可以消除噪声偏差,而且当信号发生突变时,还可以保留信号的一些特性,对解决NLOS产生的测量误差有很好的抑制作用。本文首先利用小波分析理论[8]对NLOS环境下的TOA进行去噪并修正测量值,然后利用残差加权算法[9]计算定位点初始估计值,并利用最小二乘估计进行室内三维定位,最后进行仿真验证。

1 信道模型

为了很好地模拟室内环境,合适的信道模型选择非常重要。本文选择适用于室内定位环境仿真的信道COST259[10],其无线电环境的特征由多个外部参数定义,如频带、基站(BS)和天线(MS)的平均高度等。

2 算法描述

本节主要介绍NLOS环境下三维定位算法中涉及到的技术。

2.1 小波去噪

小波去噪的应用领域相当广泛,其目的是通过一系列的信号变换提取出原始信号没有直接给出的信息,如图1所示。小波去噪的原理为:选取合适的小波,对原始信号进行小波变换,按振幅的大小将信号分为有用信号和噪声信号;选取合适的阈值,保留大于阈值的噪声系数,对小于阈值的噪声系数进行处理;重构去噪后的小波系数,恢复出有用信号[11]。

图1 小波去噪原理Fig.1 Principal of wavelet denoising

在小波变换中输出信号就是接收信号,扩展滤波和小波滤波的卷积表示为

y(n)=Wr(n)=r(n)*H(n)*G(n)

式中:G(n)为信号的高频部分;H(n)为信号的低频部分;y(n)为要得到的信号;r(n)为原始信号;W为小波函数;*为卷积计算;n为测量数据的数量。

图2 3层小波分解Fig.2 Decomposition of three-layer wavelet

2.2 基于残差加权算法的三维定位算法

在室内定位算法中常常利用Chan算法提供一个适当的初始估计位置信息。如果提供的初始位置信息不当,Chan算法的收敛就受到影响,继而影响到定位精度。Chan算法是一种以非递归方式分析表达式的算法,计算量较小,但在室内环境中的定位精度较差。为了保证室内定位算法的定位精度,必须找到一个可以提供更好初始位置的算法。本文首先通过小波变换矫正TOA测量值以保证初始估计位置更靠近实际位置,然后使用残差加权算法对初始位置进行计算。

设待定位点M的坐标为(x,y,z),基站坐标为(xi,yi,zi),则基站与待定位点之间的距离

i=1,2,…,N

(1)

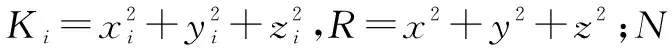
(2)

进一步简化为

(3)

h=GaLa

(4)

(5)

假设La,0为La的真实值,其中包括了M的真实位置,误差向量ψ的计算公式为估计值减去真实值,即

ψ=h-GaLa,0

(6)

得出其最小二乘解为

La=argmin{(h-GaLa,0)Tψ-1(h-GaLa,0)}=

(7)

ψ可以用TOA校正值的协方差矩阵Q代替,即

(8)

若TOA各测量值间相互独立,则Q为一对角矩阵,如下所示:

(9)

TOA矫正后的误差向量

ψ′=2Bn+n·n≈2Bn

(10)

其中,

式中:n为噪声。误差向量ψ′对应的协方差矩阵

φ=E(ψ′ψ′T)=4BQB

(11)

使用最小二乘算法得到La的最大似然估计值,如下所示:

(12)

Q是未知的,Q的选取决定了定位精度。本文利用残差加权算法来计算Q。

(13)

得到残差平方和

(14)

(15)

(16)

则La的近似值为

(17)

从求解的结果可以估计矩阵B的值。然而,当基站离待估计点较近时,矫正后TOA测量值仍存在一定的误差,为了得到更加准确的估计位置,必须进行二次加权最小二乘估计,通过扰动算法计算La的协方差矩阵[13]。有噪音干扰时,

Ri=Ri，0+cni,Ga=Ga，0+ΔGa,h=h0+Δh

(18)

设Ga,0La,0=h0,则式(6)可转化为

ψ′=Δh-ΔGaLa,0

(19)

由式(4)和式(19)可得到

(20)

La为一个随机变量,可以表示为

(21)

(22)

(23)

这里ψ′-1为误差的协方差矩阵,如下所示:

4B′cov(La)B′

(24)

(25)

最终得到M的定位结果为

3 仿真及结果分析

为了验证算法的合理性,本文对算法进行仿真,并与Chan[14]算法进行比较。采用COST259信道模型,基站分布形式为由7个基站组成的蜂窝式结构,其中至少有2个基站数据含NLOS误差。对不同小区半径和不同NLOS误差条件下定位点的均方根误差进行比较,如图3和图4所示。

图3 不同小区半径下3种算法均方根误差比较Fig.3 Comparison of RMSE among three algorithms for different diameters

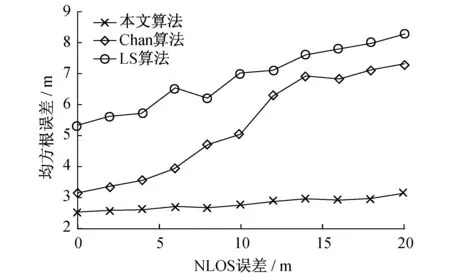
图4 不同NLOS误差条件下3种算法均方根误差比较Fig.4 Comparison of RMSE among three algorithms for different NLOS errors

图3为在不同小区半径下3种算法的比较。从图3可以看出,在不同小区半径下本文提出的算法稳定性和定位精度更高。随着小区半径的增加,LS算法的定位精度变差。在小区半径为2 000 m时,本文算法的定位精度最佳。

图4为不同NLOS误差条件下3种算法的比较。从图4可以看出,本文提出的算法更稳定,能明显改善定位精度。通过小波去噪和二次加权最小二乘估计,使算法性能进一步改善。在NLOS误差较小时,Chan算法定位精度和本文算法的定位精度相差较小,这是由于Chan算法可以采用高斯测量噪声抑制能力来抑制NLOS[15]。然而,随着NLOS误差的增加,Chan算法的表现变差。

4 结语

根据室内NLOS环境的复杂性,本文提出了抗NLOS室内定位算法。利用小波去噪的原理抑制NLOS误差,提高TOA的准确性,并结合残差加权算法获得精确的定位点初始估计值,进一步通过最小二乘算法计算出目标位置。该算法简单,计算量比Taylor算法小,定位精度高,符合室内定位的要求。

参考文献:

[1] BALANIS C A.Antenna theory:analysis and design[M].Hoboken:John Wiley & Sons,2005.

[2] LAN Z,FENG C,YAO Y.Research on hybrid location algorithm with high accuracy in indoor environment[C]//Chinese Control Conference(CCC).Hangzhou:[s.n.],2015:8764-8767.

[3] CONH L,ZHUANG W.Hybrid TDOA/AOA mobile user location for wideband CDMA cellular systems[J].IEEE Transactions on Wireless Communications,2002,1(3):439-447.

[4] HUANG J,XUE Y,YANG L.An efficient closed form solution for joint synchronization and localization using TOA[J].Future Generation Computer Systems,2013,29(3):776-781.

[5] JOHANNES W,FABIAN H,SCHINDELHAUER C,et al.Calibration-free TDOA self-localisation[J].Journal of Location Based Services,2013,7(2):121-144.

[6] MARY G I,PRITHIVIRA V.UWB localization techniques for precision automobile parking system[C]//Electromagnetic Interference & Compatibility.Bangalore:[s.n.],2008:621-626.

[7] MOLISCH A F,ASPLUND H,HEDDERGOTT R,et al.The COST259 directional channel model,Part I:overview and methodology[J].IEEE Transactions on Wireless Communications,2006,5(12):3421-3433.

[8] 张阳,王嘉梅.一种改进的小波变换域的字符定位方法[J].微型机与应用,2011,30(18):35-37.

ZHANG Yang,WANG Jiamei.An improved character localization method in wavelet transform domain[J].Microcomputer and Applications,2011,30(18):35-37.

[9] CHEN P C.A non-line-of-sight error mitigation algorithm in location estimation[C]//IEEE Wireless Communications and Networking Conference.[S.l.]:IEEE,1999:316-320.

[10] ASPLUND H.A channel model for position:COST259 TD20[S].Bern:[s.n.],1998.

[11] RAY P,MAITRA A,BASURAY A.A new threshold function for denoising partial discharge signal based on wavelet transform[C]//2013 International Conference,Image Processing & Pattern Recognition.[S.1.]:IEEE,2013:185-189.

[12] 王慧琴.小波分析与应用[M].北京:北京邮电大学出版社,2011.

WANG Huiqing.Wavelet analysis and application[M].Beijing:Beijing University of Posts and Telecommunications Press,2011.

[13] 屠晓东.基于UWB信号的多基站与单基站定位算法的研究与性能分析[D].青岛:中国海洋大学,2012.

TU Xiaodong.Research and performance analysis of multiple base station and single base station positioning algorithms based on UWB signals[D].Qingdao:Ocean University of China,2012.

[14] 章坚武,唐兵,秦峰.Chan定位算法在三维空间定位中的应用[J].计算机仿真,2009,26(1):323-326.

ZHANG Jianwu,TANG Bing,QIN Feng.Application of Chan location algorithm in 3-dimentional space location[J].Computer Simulation,2009,26(1):323-326.

[15] XIE W,YANG J,XIE H.A residual weighting algorithm of NLOS error mitigation for indoor ultra-wideband locating[C]//IEEE 2012 International Conference on Systems and Informatics.[S.1.]:IEEE,2012:1417-1421.