实值形式背景下概念格的渐进式并行构造算法
2018-06-20郭泽蔚李金海
郭泽蔚,姜 麟,李金海
(1.昆明理工大学 理学院,云南 昆明 650500;2.昆明理工大学 数据科学研究中心,云南 昆明 650500)
形式概念分析(Formal concept analysis)是20世纪80年代初期由德国教授R.Wille提出的一种用于发现知识的理论。形式概念分析通过构造概念格来进行数据的处理,也称概念格理论[1]。以往关于概念格的研究主要集中于经典的形式背景,即属性值为Boolean值,然而,由于现实中数据的复杂性,更多的形式背景中的属性值是区间形式的普通实值。经典的概念格主要应用于发现二值(或多值)形式背景的概念构造,因此,传统形式背景中概念格的构造方法并不适用于实值形式背景[3-4]。而实值形式背景概念格的构造存在算法复杂性大等缺陷,现阶段围绕这一类问题的研究也缺少较好的普适性,故进一步讨论实值概念格的构造具有一定的意义。
Matlab已成为数值计算领域的主流工具,其拥有的并行计算工具箱(Parallel computing toolbox,PCT)和并行计算服务(Distributed computing server,DCS)可以实现基于多处理器平台和集群平台的多种并行计算任务,利用PCT和DCS,用户无需关心多核、多处理器之间以及集群之间的底层数据通信,可以将更多的精力放在并行算法的设计,充分利用Matlab提供的数值计算模块和数据显示功能,高效便捷的完成并行计算任务[5]。
经典形式背景下的建格算法并不适用于处理实值形式背景下的概念格,而串行算法在数据规模较大的情况下计算效率较低。针对实值形式背景的特点,结合经典概念格的渐进式构造思想,本文首先给出了计算实值概念格的方法;然后提出了一种实值概念格计算的渐进式构造算法,并对其进行改进,得到并行算法,应用Matlab对串、并算法进行程序的实现;最后通过数值实验对该算法的串行与并行运行效率作了对比,对该算法在特定实值条件下的并行化可行性进行了评估。
1 实值形式背景与实概念格
1.1 实 集
定义1[6]设R为实数集。对于μ,v∈R,称I=[μ,v]为R上的一个实区间,其中μ和v分别称为实区间I的上界和下界。如果μ>v,则称实区间I是空的,记为[,]。
显然,当I=[μ,v]非空时,I就是由μ到v之间的全部实数构成的集合。对于两个实区间I1=[μ1,v1]和I2=[μ2,v2],它们的交Inter(I1,I2)满足:
Inter(I1,I2)=[max(μ1,μ2),min(ν1,ν2)]
定义{I1,I2}的闭包为
Closure({I1,I2})=
n个实区间的闭包算子可表示如下:
Closure({I1,I2,…,In})=
Closure({Closure({I1,I2}),…,In})


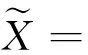
并记U上所有实值构成的集合为R(U)。
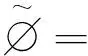
集合中的交运算和并运算也同样适用于实集,实集中有两种交(并)运算,分别为L-交(并)和S-交(并)。下面给出定义[7]。
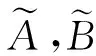

1.2 实值形式背景与实概念格


例1表1给出了一个实值形式背景。
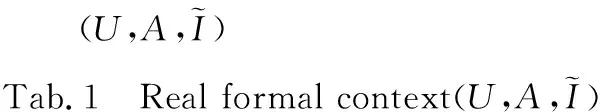
表1 实值形式背景


(∀X∈P(U))
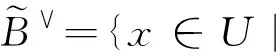
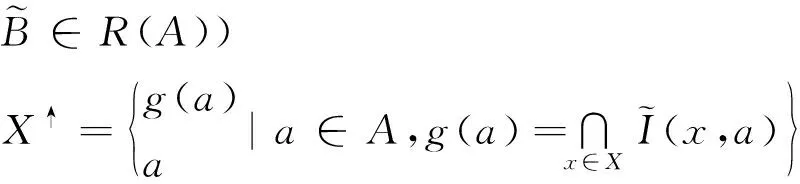
(∀X∈P(U))




根据前面的讨论,对于实值形式背景,可构造两类实概念格:L-实概念格和S-实概念格。然而,这两种概念格框架的构建及相关讨论是类似的,故在此只给出基于L-实概念格构建的背景属性框架。需要指出的是,只要将该约简框架的中所有与L-实概念格相关的符号都替换为S-实概念格中相应的符号,就可以得到基于S-实概念格构建的实值形式属性背景框架。
1.3 概念格的构造算法
概念格的构造过程实际上就是概念聚类的过程,概念格一个重要的属性就是其完备性使得对于同样的一个数据集,每次生成的格都是唯一的,即对象、属性的排列顺序和格构造算法均不会影响其构造的结果。因此,现有的关于概念格的构造算法都是为了提高建格的效率,减少建格的复杂度而设计的[9]。经典形式背景概念格的串行构造算法大致可分为两类:批处理算法、渐进式算法。
批处理算法主要思想:首先要生成所有的格节点,即原形式背景中所有的概念的集合,然后根据它们之间的前驱-后继关系生成边,完成格的构造。比较经典的有Bordat算法[10-11]。批处理算法自顶向下通过递归的方式构造其子节点,并展开运算,这种算法有利于消掉不满足规则的节点,提高算法效率。

2 实值形式背景概念格构造算法
2.1 设计实值概念格的渐进式构造算法
以往围绕概念格构造算法的研究主要集中于经典形式背景,而实值形式背景概念格的算法构造目前并没有充分的研究成果。原因是实值形式背景的转化较为困难,而且算法的复杂性非常大,对数据的适应性很差[8]。受Godin渐进式算法的启发,下面给出一种实值形式背景概念格提取的算法Real。
Algorithm Real
输入:原始实值形式背景L
输出:实概念矩阵L*
BEGIN
size(L)=[m,n];
L0=(∅,[]);/*初始化概念*/
Xi=sealing(Xi);/*将对象序号0-1化*/
L_new=(X1,B1);/*存储每次循环结束时所有概念*/
FORi=2:m
size(L_new)=[m_1,n_1];/*更新L_new中概念的个数*/
将(Xi,Bi)加入到L_new;
FORj=1:m_1
Z=Xi|Xj;
FORr=1:(n_1)/4
BZr=Bjr∪Bir;/*Xi和Xj在属性r下对应的区间比较*/
BZ=[BZBZr];
ENDFOR
L′=(Z,BZ);
IFL′
单独形成一个概念
将概念L′添加进L_new;
ENDIF
ENDFOR
L_new=xiao(L_new);/*消除冗余概念*/
ENDFOR
L*=L0∪L_new;
END
该算法继承了传统概念格渐进式构造算法的核心思路,即通过创建一个存储概念的新格L_new,通过循环检验每次添加新节点后L_new中概念是否发生变化,继而更新概念集合进入下次循环,这样做的好处在于算法可以在不停地添加新节点的同时,对已形成的边进行维护,通过1.1节中描述的实值概念格提取规则的检验,增加相应的边,消除冗余的边,当所有的概念添加完毕后,完成构造。
针对实值形式背景取值复杂的特点,采用闭包算子的思想单独在算法中设计子函数对区间值进行比较。
2.2 算法的并行化改造与实现
实值形式背景的概念格构造算法之所以复杂程度高,是因为在同一属性下不同对象的取值是由单个区间或多个不相交的区间组成的集合,它们之间的交并运算在算法设计中要考虑的情况既多又繁杂,因此,将串行算法进行并行化处理,是提高算法运算效率的有效途径[14]。下面给出对算法Real进行改进后得到的并行算法Para-Real。
Algorithm Para-Real
输入:原始实值形式背景L
输出:实概念矩阵L*
BEGIN
size(L)=[m,n];
L0=(∅,[]);/*初始化概念*/
Xi=sealing(Xi);/*将对象序号0-1化*/
Z_new=X1;
将Xi加入到Z_new;
size(Z_new)=[m_1,n_1];/*更新L_new中概念的个数*/
FORj=1:m_1
Z=Xi|Xj;
将Z加入到Z_new;
ENDFOR
ENDFOR
PARFORr=1:(n-1)/4/*将形式背景中的数据按属性进行分组执行*/
B_newr=B1r;
FORi=2:m
将Bir加入到B_newr;
size(B_new)=[m_1,n_1];
FORj=1:m_1
BZr=Bjr∪Bir;/*Xi和Xj在属性r下对应的区间比较*/
将BZr加入B_new;
ENDFOR
ENDFOR;
B_new=[B_newB_newr];
ENDPARFOR
L_new=xiao(L_new);
L_new=[Z,B_new];
L*=L0∪L_new
END
由于Real算法的思想是在不断添加新边的同时又不断更新概念,因此消除冗余概念的算法是在生成概念的算法中进行嵌套,而程序可以并行执行的前提是算法可以分成多个单元交由多个核心同时计算并最后整合。因此,Para-Real的思想是:先将原实值形式背景按属性的个数n划分成纵向量[m,1]的形式,每组向量各自单独执行概念的生成算法(注:在不进行消除算法的情况下,各组向量生成的带冗余的概念总数相同),最后合并再进行消除。
2.3 并行算法的实现
Matlab提供的多种并行计算的方式,其中MDCS是基于搭建集群的一种分布式计算服务,在搭建好之后,可以通过一台主机向集群中的其他机器分配任务,最后各机器将计算结果返回主机,主机整合任务,完成计算任务[5]。步骤如下:
1)mdce start/*MDCE实际上是一个进程*/
2)startjobmanager/*启动一个任务管理进程*/
3)startworker/*需要启动在sceduler中注册过的若干个worker用于执行任务*/
4)创建作业并提交至任务执行队列
5)返回结果,并销毁作业任务释放内存。
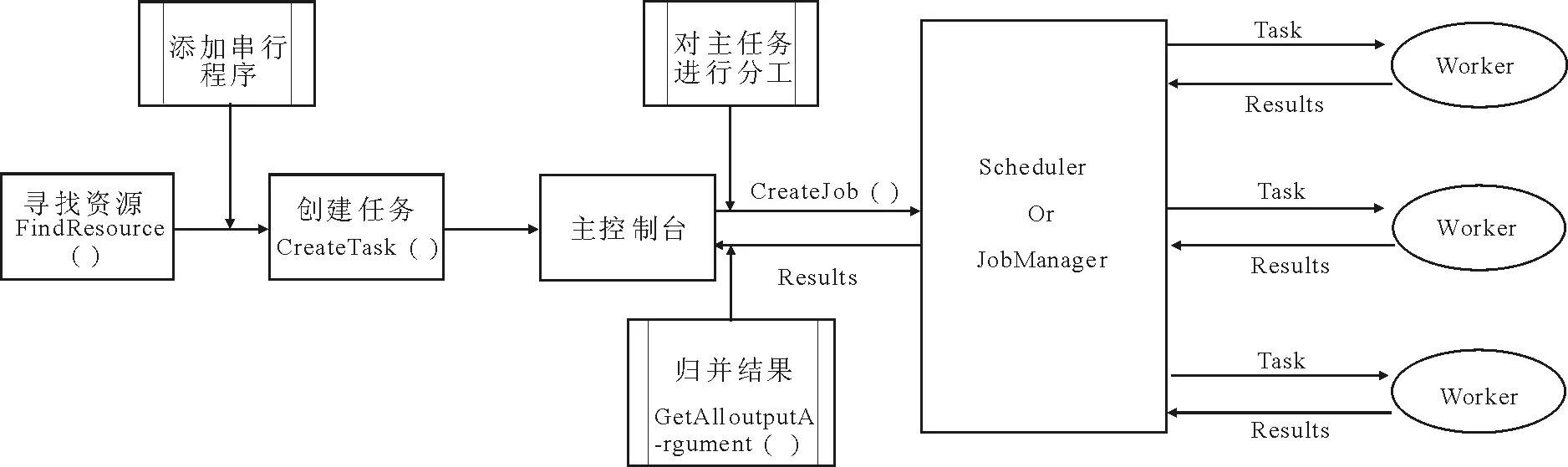
图1 集群上算法的并行计算流程Fig.1 Parallel Computing Program of Algorithm in Cluster
上述Par-Real算法的并行处理流程如图1所示。利用findResource()函数调出已经创建好的一个集群任务管理对象,打开Matlab的并行计算池,运行Par-Real算法程序,创建的任务提交至任务队列中,通过JobManager为各个worker分配任务,worker执行完任务将结果返回给JobManager,JobManager归并结果,并返回给主控制台。
3 数值实验
本节通过数值实验对上一节提出的算法Real进行评估。由于实值形式背景的复杂性,本节实验需要一些中、大型的实值形式背景,经过实验验证[15],对于两个对象和属性个数相同的实值形式背景M1和M2,可以融合构造一个新矩阵:
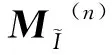

实验环境采用Matlab 2012a Win64版本(含License Manager 11.9),并行计算平台为MATLAB Distributed Computing Server 6.0,编译环境为Microsoft Visual C++2010。MDCE集群由一台主控制节点和两台从节点构成,主节点配置为Inter(R)Core(TM)2 Quad CPU Q6600 @2.40GHz,4.00GB内存和500GB硬盘。从节点的配置为AMD phenom(tm)8400 Triple-Core Processor 2.10 GHz,3.25GB内存和300GB硬盘。其他采用系统默认配置。


表2 实值形式背景
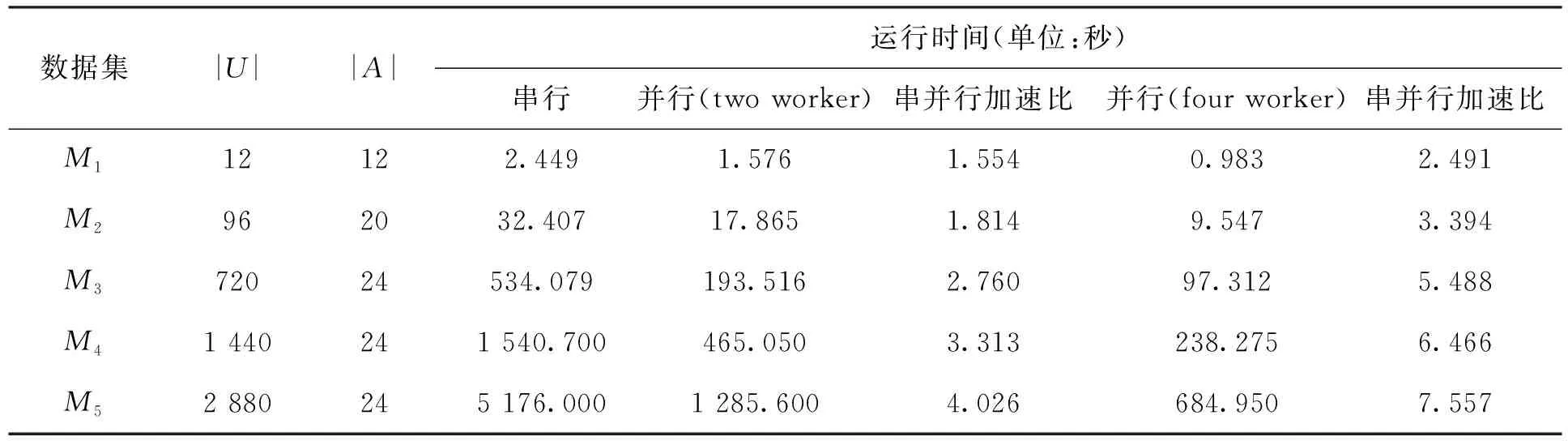
表3 串、并行算法对比Tab.3 Comparison of Serial and Parallel Algorithms
表3中根据得出的串行和并行运行时间数据,分别计算了two worker和four worker情况下的串并行加速比(串行时间/并行时间)。可以看出,在数据量小的情况下,并行的效率比数据量大时低,这是因为并行的核心之间有数据通信,如果通信时间相对于计算时间所占的比例较高时,那么数据通信对并行效率的影响较大。随着数据量的增大,运行时间的串并行加速比逐渐增大,并行的效率提高。当worker数增加,并行的效率进一步得到提高,这说明当条件允许的情况下,计算单元增加或集群中加入的计算机数量增加,都有助于进一步提高构造实值概念格并行算法的效率。
需要说明的是,实值形式背景的数据结构较为复杂,因而构造实值概念格的过程中算子的设计更为复杂,相较于文献[7]中最高达到320个对象|U|,本文实验的数据量仅提高了一个数量级,在面对大量数据集的概念格提取问题上,算法的改进还需要进一步的探索。
4 结 语
针对实值形式背景,本文结合了经典概念格渐进式构造算法时间性能好、稳定等特点,提出了一种构造实值概念格的算法Real,同时对其在Matlab集群环境下进行了并行化处理,通过实验验证了串并行算法的可行性,并给出实验结果,对比了串并行运行时间加速比的变化,表明并行计算在数据量大的时候效率更高,计算节点越多并行算法相对串行算法的优势越明显。由于算法的复杂性大,该算法在数值信息过大时并没有很好的适应性,下一步的工作需要寻找更好的方法来提高算法效率。进一步讨论实值形式背景中的对象约简问题和决策分析对概念格构造算法效率的提高有借鉴意义。
参考文献:
[1] WILLE R. Restructuring lattice theory: An approach based on hierarchies of concepts[J]. Orderd Sets D Reidel, 1982, 83:314-339.
[2] 李金海, 邓硕. 概念格与三支决策及其研究展望[J]. 西北大学学报(自然科学版), 2017, 47(3):321-329.
[3] 钱婷, 贺晓丽. 区间集概念格的构造理论研究[J]. 西北大学学报(自然科学版), 2017, 47(3):330-335.
[4] 杨建峰, 魏玲. 基于差别矩阵的区间值形式背景属性约简[J]. 西北大学学报(自然科学版), 2012, 42(3):365-369.
[5] 刘维. 实战Matlab之并行程序设计[M]. 北京:北京航空航天大学出版社,2012.
[6] JAOUA A, ELLOUMI S. Galois connection, formal concepts and Galois lattice in real relations: Application in a real classifier [J]. The Journal of Systems and Software, 2002, 60: 149-163.
[7] 李金海. 面向规则提取的概念格约简方法及其算法实现[D]. 西安:西安交通大学, 2012.
[8] YANG H Z, LEUNG Y, SHAO M W. Rule acquisition and attribute reduction in real decision formal contexts[J].Soft Computing,2011, 15(6): 1115-1128.
[9] LI Y, LIU Z T, SHEN X J, et al. Theoretical research on the distributed construction of concept lattices[C]∥International Conference on Machine Learning and Cybernetics. IEEE, 2003,1:474-479.
[10] BORDAT J P. Calculpratique du treillis de Galois d′unecorrespondance[J].Matheématiques Informatiques Et Sciences Humaines, 1986, 96: 31-47,101.
[11] GANTER B. Two basic algorithms in concept analysis[C]∥International Conference on Formal Concept Analysis. Springer-Verlag, 2010: 312-340.
[12] GODIN R, MISSAOUI R, ALAOUI H. Incremental concept formation algorithms based on Galois (concept) lattices [J]. Computational Intelligence, 1995, 11(2): 246-267.
[13] LI J H, MEI C L, LV Y J. Incomplete decision contexts: Approximate concept construction, rule acquisition and knowledge reduction [J]. International Journal of Approximate Reasoning, 2013, 54(1): 149-165.
[14] 张磊. 基于同义概念和同类概念的概念格并行构造模型[D].开封:河南大学,2006.
[15] 王磊, 魏玲, 姚广. 横向合成背景的概念生成[J].西北大学学报(自然科学版), 2010, 40(2):195-198.
