基于SIFT与K-means的图像复制粘贴篡改检测

叶雨晴，邱晓晖

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

近年来，随着图像处理软件的日益普及，人们可以轻而易举地对一幅数字图像进行随意修改。一些不法分子通过伪造、篡改图像实现非法目的，不但影响到版权保护，而且给新闻报道、商业宣传、法庭取证的真实性和可靠性都带来了前所未有的挑战。在这种背景下，图像篡改检测技术应运而生。图像篡改方式多种多样，其中复制粘贴是一种较常见、较隐蔽的篡改方式。图像复制粘贴即选择图像的一个或多个区域，在进行旋转、缩放、光照变换等操作后复制粘贴到同幅图像[1]，以达到增加或掩盖目标的目的。

目前，针对复制-粘贴篡改的盲检测主要分为两种方法:

(1)基于块匹配的图像盲检测方法。该方法是通过对图像进行分块，计算每个块的不变特征向量，并在此基础上对特征向量通过字典排序等方法进行相似块匹配。Fridrich等[2]利用量化DCT系数作为图像特征；Popescu等[3]采用PCA表征图像块，进一步提高了算法检测效率，但算法的鲁棒性不强；Li等[4]通过小波变换提取图像的低频子带分量。该类基于块匹配的算法对平滑区域的篡改图像检测率较高，但对于经过旋转、缩放等操作的篡改图像鲁棒性较差。

(2)基于特征点匹配的图像盲检测方法。该方法是通过搜索图像的局部角点或极值点并在去除错误特征点后进行图像匹配。该类方法包括Harris角点检测[5]、基于SIFT[6]、SURF[7]算法、ORB算法[8]等，这类算法在处理图像之间发生平移、旋转、仿射变换情况下的匹配问题上具有良好的检测效果[9]。其中SIFT算法提取的特征点比较稳定,具有抗光照和抗几何形变的能力，但是该算法仍存在一些不足，比如特征描述符的维数过大以及耗时过长。

针对图像复制粘贴篡改操作，以图像特征点匹配为切入点，对传统SIFT算法特征向量维数过高的缺点，对SIFT算法进行改进。

1 SIFT算法简介

尺度不变特征变换(scale-invariant feature transform，SIFT)是一种在尺度空间寻找极值点，并提取其位置、尺度、旋转不变量的算法。SIFT特征提取需要以下几个步骤:

(1)尺度空间的构建。

通过构建尺度空间，可以模拟数字图像多尺度特性。一幅图像尺度空间L(x,y,σ)的定义如下:

L(x,y,σ)=G(x,y,σ)*I(x,y)

(1)

其中，(x,y)表示图像中每个像素的位置；σ表示尺度空间大小因子；G(x,y,σ)为高斯卷积核:

(2)

(2)尺度可变高斯函数的表示。

为了在尺度空间中有效地检测稳定的关键点，将相邻两尺度空间函数相减构造高斯差分函数(DOG)金字塔模型。DOG算子如下：

D(x,y,σ)=L(x,y,Kσ)-L(x,y,σ)

(3)

其中，L(x,y,σ)表示尺度为σ的尺度空间；L(x,y,Kσ)表示尺度为Kσ的尺度空间。

(3)计算关键点。

DOG尺度空间极值点即为SIFT算法特征点。图1所示为DOG尺度空间3个相邻尺度。每个检测点与邻域8个相邻点以及上下相邻尺度9×2个点共26个点同时进行比较，以确保在尺度空间和二维图像空间内所检测内容为局部极值。

(4)关键点的精确定位。

由于DOG值对噪声和边缘敏感，因此要剔除低对比度点和边缘点。通过对DOG函数的二阶泰勒展开式求导精确定位极值点并求出极值D(X)，同时利用极值点处Hessian矩阵的性质去除边缘点，以增强匹配稳定性、提高抗噪声能力。

(4)

(5)特征主方向的提取与描述子的生成。

为使描述符具有旋转不变性，根据局部特征为每个关键点分配一个基准方向[10]。SIFT中使用梯度直方图的方法求取局部结构的稳定方向。在特征描述上，Lowe建议描述子为关键点邻域尺度空间内4×4的窗口中计算每个窗口内的8个方向的梯度信息，生成128(4×4×8)维向量表征。

2 基于改进SIFT算法的图像复制粘贴篡改检测

由于SIFT关键点特征向量具有很高的维度，导致其时间复杂度较高。PCA-SIFT[11]作为其改进算法，使用更加精简的方法构建特征点描述向量，利用图像特征主要成分来实现降低维数的目的，但由于PCA采用线性降维的方法，未考虑描述子各局部特征的非线性关系，使得对部分局部关键信息表述不够完整。而K-means聚类算法是一种既可以用于线性，也可以用于非线性的聚类方法[12]，基于此，文中算法采用K-means聚类的思想对SIFT算法进行改进。

2.1 利用K-means对SIFT特征向量降维

对比PCA-SIFT的优劣情况，采用基于K-means聚类的方式对SIFT 算法进行降维。通过对SIFT生成的特征向量矩阵的列向量进行聚类，并提取与SIFT特征矩阵整体差异度最小的一类特征向量进行匹配，进而完成对SIFT特征向量的降维。该类特征向量，最大保持了原有特征点的成分，并且相比于PCA-SIFT算法只能够线性降维[13]。文中算法考虑了局部特征的非线性关系，不仅对平移操作检测效果好，而且对于进行缩放、旋转操作的复制粘贴篡改图像的检测同样具有很高的鲁棒性。

2.1.1 K-means聚类算法

K-means算法能够以较低维度表示高维度数据的局部信息[14]。其原理是将给定的n个数据点的数据集X分为k类，在不断地循环迭代中使其目标函数达到最小，从而使同一类内的数据差异性小，不同类之间的数据具有一定的分离性[15]。

2.1.2 基于K-means的改进SIFT算法

K-means初始聚类中心的选取直接影响聚类的结果[16]。文中通过计算得到平均差异度最小的SIFT特征矩阵列向量，即与特征矩阵差异最小的列向量作为初始聚类中心c1。聚类完成后，划分到c1所在类的特征矩阵与整体差异最小、最相似。提取该类的特征向量进行匹配，不仅最大保持了原有特征向量的成分，而且大大降低了特征向量的维数。

平均差异度di的定义如下：

(5)

(6)

其中，设SIFT关键点个数为m，xi,xj为两个m维SIFT特征矩阵列向量；dij为xi,xj的距离；N为列向量的总数。平均差异度越小，样本与整体越相似。

假设SIFT算法提取到的特征点个数为m，则得到的特征向量矩阵T的大小为m×128。基于K-means的改进SIFT算法具体步骤如下：

(1)选取k个初始聚类中心c1,c2,…,ck。首先计算特征矩阵T列向量两两之间的距离dij，然后计算平均差异度di最小的列向量，作为第一个初始聚类中心c1；选取距离c1最远的点作为第二个中心点c2，选取距离c1和c2最远的点，作为c3，依次计算中心点c4,c5,…,ck。

(2)对特征向量矩阵T中的每个列向量xi，计算其与各个聚类中心ck的欧氏距离并将其归为距离最小的类。

(3)根据式7求得各聚类中心数据的平均值进而更新聚类中心ck。

状态监测系统提供丰富直观的、可组态的多个监测画面，从不同的角度、分层次展现机组的状态信息。监测画面中将各种监测状态以图表、图形、数据等形式展示出来。

(4)重复步骤2和步骤3，直到聚类中心基本稳定或迭代次数达到上限结束。

2.2 基于改进SIFT算法的图像复制粘贴篡改检测步骤

(1)读取待检测图像I，利用SIFT算法提取图像的关键点，生成关键点的128维SIFT特征向量。

(2)利用改进的K-means算法对特征向量矩阵T的128维列向量进行聚类，将列向量分为k类。

(3)对划分到第一类的t维特征向量进行特征匹配，定位复制粘贴区域并用线标出。特征匹配的具体步骤如下：

首先计算特征向量间的欧氏距离，其次在篡改图像中遍历每个关键点以找出与这个关键点欧氏距离最近和次近的两个关键点。如果满足式7,就认为是一对复制粘贴匹配点，最终确定篡改区域。

(7)

其中，Dnearest为最近欧氏距离；Dhpyo-nearest为次近欧氏距离。

算法流程如图2所示。

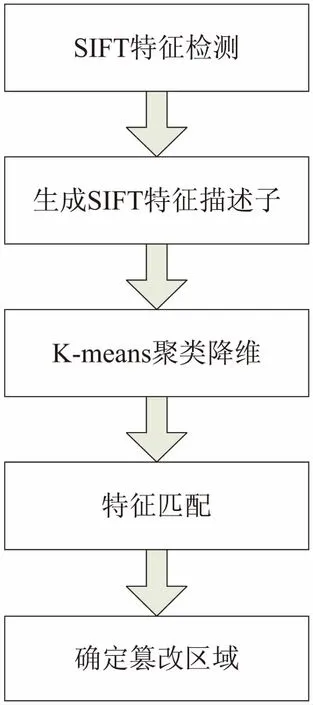
图2 基于K-means的改进SIFT算法流程

3 实验结果分析

实验中PC配置为CPU 3.20 GHz，内存4 G，仿真平台为MATLAB R2016a。为了验证该算法对篡改检测性能的影响，设计了一系列实验，对平移、旋转、缩放等不同后处理下的图像分别采用经典的SIFT、PCA-SIFT算法以及提出的基于K-means的改进SIFT算法进行仿真，然后从匹配的正确率和匹配点数以及检测时间上进行比较。仿真结果如图3所示。

图3 仿真结果

从表1～3可以得出以下结论：

(1)正确率：无论是PCA-SIFT算法还是文中算法都继承了SIFT算法对于尺度变换和旋转的鲁棒性。

(2)匹配精确度：由于PCA是一种线性降维方法，对于具有线性特征分布的特征点能够起到很好的降维作用，如图(c)，能够保留足够的特征点用于复制粘贴区域的匹配，但对于非线性分布的特征点，该算法无法保留足够的特征点，如图(g)、(k)，很多特征点被去除，匹配精度很低。而文中算法，在保证匹配点数的同时，提高了检测效率。

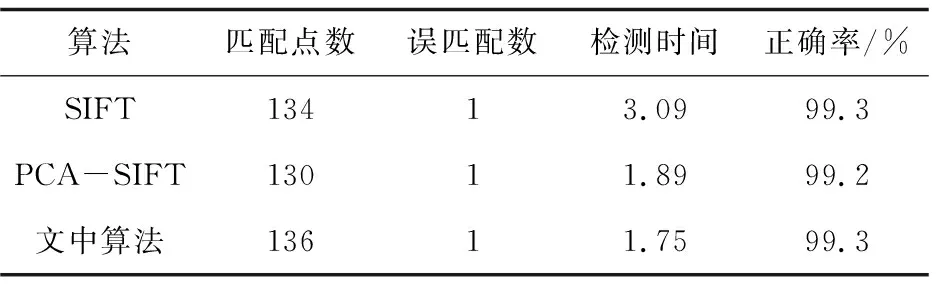
表1 平移操作下的各类算法检测结果对比

表2 旋转操作下的各类算法检测结果对比

表3 缩放操作下的各类算法检测结果对比

4 结束语

基于SIFT算法，将K-means算法用于SIFT特征向量的降维，节约了图像复制粘贴篡改检测过程中特征匹配的时间。实验结果表明，利用该算法进行图像复制粘贴篡改检测，既保持了传统SIFT算法的稳定性和精确性的优点，又比SIFT算法以及PCA-SIFT算法具有更高的检测效率。

参考文献:

[1] 柴新新,邱晓晖.基于提升小波变换的图像篡改检测算法[J].计算机技术与发展,2016,26(4):78-81.

[2] FRIDRICH J,SOUKAL D,LUKJ.Detection of copy-move forgery in digital images[C]//Proceedings of digital forensic research workshop.Cleveland:IEEE,2003:55-61.

[3] POPESCU A C,FARID H.Exposing digital forgeries by detecting traces of resampling[J].IEEE Transactions on Signal Processing,2005,53(2):758-767.

[4] LI Weihai,YUAN Yuan, YU Nenghai. Passive detection of doctored JPEG image via block artifact grid extraction[J].Signal Processing,2009,89(9):1821-1829.

[5] HARRIS C G,STEPHENS M J.A combined corner and edge detector[C]//Proceedings of alvey vision conference.[s.l.]:[s.n.],1988:147-151.

[6] LOWE D G.Distinctive image features from scale-invariant key-points[J]．International Journal of Computer Vision,2004,60(2):91-110.

[7] BAY H,TUYTELAARS T,GOOL L V.SURF:speeded up robust features[C]//Proceedings of the 9th European conference on computer vision.Graz,Austria:Springer-Verlag,2006:404-417.

[8] RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB:an efficient alternative to SIFT or SURF[C]//Proceedings of the 2011 international conference on computer vision.[s.l.]:IEEE,2011:2564-2571.

[9] 林 晶,黄添强,林玲鹏,等.采用局部强度顺序模式的图像复制—粘贴篡改检测算法[J].通信学报,2016,37:132-139.

[10] 何林远,毕笃彦,马时平,等.基于SIFT和MSE的局部聚集特征描述新算法[J].电子学报,2014,42(8):1619-1623.

[11] LUO Juan,GWUN O.A comparison of SIFT,PCA-SIFT and SURF[J].International Journal of Image Processing,2009,3(4):143-152.

[12] 张宁丽,马 燕,李顺宝,等.FKPCA-SIFT算法在图像匹配中的应用[J].电视技术,2015,39(7):21-24.

[13] 李 翠,冯冬青.基于改进K-均值聚类的图像分割算法研究[J]．郑州大学学报:理学版,2011,43(1):109-113．

[14] 朱 叶,申铉京,陈海鹏.基于混合灰度序模式的图像复制-粘贴篡改盲鉴别算法[J].吉林大学学报:工学版,2017,47(4):1280-1285.

[15] 李昆仑,孙 硕.基于改进SIFT算法的图像复制粘贴篡改检测[J].计算机科学,2016,43(6A):179-183.

[16] 杜振龙,杨 凡,李晓丽,等.利用SIFT特征的非对称匹配图像拼接盲检测[J].中国图象图形学报,2013,18(4):442-449.