±800 kV“U”型SF6气体绝缘穿墙套管绝缘性能分析
2018-06-19
(国网重庆市电力公司电力科学研究院,重庆401123)
0 引言
高压直流输电定位于大型能源基地的远距离、大容量外送,随着我国±800 kV特高压直流输电技术的迅速发展,一些特高压直流电力设备的研制水平也得到显著提升,其中就包括用于特高压换流站阀厅的穿墙套管。该套管作为换流站直流场和阀厅的连接设备,在整个直流输电工程中处于“咽喉”位置[1]。直流穿墙套管有三种技术方案:油浸纸电容式结构、环氧浸纸电容式结构和纯SF6气体金属屏蔽式结构[2]。油浸纸电容式结构存在漏油、爆炸燃烧风险,不满足阀厅无油化要求;环氧浸纸电容式电气性能优良,但设计、制造难度大;纯SF6气体金属屏蔽式结构相对简单,制造难度相对较低。穿墙套管现场运行中典型照片如图1所示。

图1 现场运行穿墙套管典型照片Fig.1 The typical on-site scene of the wall bushing
现场运行经验表明:为确保特高压直流穿墙套管长期安全稳定运行,需在设计初期对其绝缘性能进行较全面分析。例如图1中空心复合绝缘子沿路径1的电位分布是否均匀,空心复合绝缘子沿面电场强度能否满足控制要求。文献[3]表明:准东-重庆±1 100 kV特高压直流输电工程中换流变压器阀侧套管将采用油浸纸电容式结构,且给出了该套管的相关技术参数。文献[4]应用有限元法计算了±800 kV纯SF6气体金属屏蔽式套管的电场分布,并分析了沿空心复合绝缘子发生闪络的原因,提出了防止复合绝缘子发生电晕放电的措施。相关文献研究表明深入了解穿墙套管在实际运行环境下三维电场分布规律是穿墙套管结构设计、绝缘性能评估的基础[5-7]。笔者将金属屏蔽式“U”型结构用于穿墙套管设计,分析了±800 kV直流穿墙套管的实际运行环境和参数,同时将有限元分析方法应用于特高压直流穿墙套管的三维电场模拟,讨论了套管闪络电压与绝缘距离之间关系,可为特高压穿墙套管的设计、制造和运行提供理论依据。
1 计算原理
高压套管结构相当复杂,存在复合绝缘结构,以及各种不规则界面,所以高压套管内外绝缘结构的电场分布也更加复杂。因此,结合工程的布置方式、应用数值仿真计算,开展特高压套管绝缘结构的电场计算与分析,不但可以研究其绝缘结构、校验初步设计,还可以根据仿真计算结果中发现的问题开展进一步的优化,完善设计[8-10]。在静电场中取电位φ为直接求解对象。各类物理场的定解问题是由对应的方程组和定解条件组成。若用有限元法求解,则首先需确定与定解问题等价的泛函问题即变分问题。现以齐次第一类边界条件的泊松场为例来说明泛函的极值问题。泊松场中泛定方程:

可以证明,该泛定方程与下列变分问题:
Uf50=ALB
d极值等价,且有唯一解。整理后可得:

在电磁场计算中极值都指极小值。式中的积分项称为对应于泊松方程的泛函,式中V表示场域。对上式进行积分变换,可得:

式中,S是包围V的闭合曲面。对于齐次第一类边界条件和齐次第二类边界条件,上式可以化简为

可以证明,在取泛函F(ϕ)极值的过程中,己自动满足齐次第三类边界条件,同时也满足非齐次第二类或第三类边界条件。该类边界条件称为自然边界条件,其相对应的变分问题称为无条件变分问题。由于在求泛函极值过程中,第一类边界条件没有被自动满足,所以在处理对应于第一类边值问题和变分问题时,还必须单独对第一类边界条件进行处理。通常称这类边界条件为强加边界条件,而相对应的变分问题称为条件变分问题。
2 计算模型
依据“U”型±800 kV穿墙套管图纸,考虑不同极板布置方式进行实体建模,±800 kV“U”型穿墙套管三维有限元模型如图2所示。

图2“U”型±800 kV穿墙套管三维计算模型Fig.2 The three dimensional simulation model of“U”type±800 kV wall bushing
图2表明“U”型穿墙套管与“一”型传统穿墙套管相比,将中心导杆分为了户内、户外两部分,避免了“一”型传统穿墙套管中心导杆过长导致的制造难度。但套管高电位均压环离墙体相同距离条件下,复合绝缘子需更长距离。“U”型穿墙套管将水平排布的中心导体结构转化为具有一定角度的倾斜布置,降低了中心导体在水平排布条件下由于长度过长、自重过大导致的导体偏心现象发生。另一方面,由于“U”型穿墙套管结构紧凑性,导致套管电场分布更为集中,增大了套管局部发生闪络的风险,因此建立了套管的三维电场仿真计算模型,对其较为精确的三维电场分布进行讨论分析,其中±800 kV穿墙套管技术参数如表1所示。

表1 ±800 kV穿墙套管技术参数Table 1 The technical parameters of±800 kV wall bushing
3 三维电场模拟结果
穿墙套管高电位均压罩和中心导杆上施加雷电冲击耐受试验电压(全波)2 300 kV,套管接地法
兰处接地施加零电位,从图3中可看出由于套管复合伞套作用,高电位由高电位均压罩逐渐降低至零电位。图4中为均压罩表面电场分布情况,其最大场强为2.727 kV/mm,低于空气中3 kV/mm的控制场强。图5和图6中为穿墙套管核心部件双层屏蔽表面电场分布情况,可见高场强区域主要集中在金属屏蔽翻边位置。双层金属屏蔽通过支撑绝缘杆连接,其场强最大值约为11.5 kV/mm,低于SF6气体中20 kV/mm控制场强。

图3 穿墙套管整体电位分布Fig.3 Overall potential distribution of the wall bushing
重点关注±800 kV“U”型穿墙套管复合伞套表面电位和电场分布情况如图7和图8所示。图中表明复合伞套户内端接地侧场强较低,高压端出现了单一峰值,其值约为704 kV/m。复合伞套户外端由于双层金属屏蔽调制作用,户外端护套表面出现两个场强峰值,其值分别为560 kV/m和356 kV/m。正是由于穿墙套管双层屏蔽对护套表面电压调制作用良好,降低了复合护套表面发生闪络的概率。

图4 均压环表面电场分布Fig.4 E-field distribution on surface of the corona ring

图5“U”型±800 kV穿墙套管屏蔽全局电场分布Fig.5 Overall E-field distribution of shielding surface of“U”type±800 kV wall bushing

图6“U”型±800 kV穿墙套管屏蔽局部电场分布Fig.6 Local E-field distribution of shielding surface of“U”type±800 kV wall bushing
4 套管结构型式选取讨论
4.1 空心复合绝缘子的设计与分析
工频和冲击电压下,套管的电气性能要求空气中的空心复合绝缘子外表面、油中的套管芯子外表面均不能发生闪络放电,套管内外绝缘的相互配合与芯子主绝缘对外绝缘的调节作用是套管外绝缘设计的关键[11-12]。套管空心复合绝缘子的干闪络电压接近于上法兰与中间法兰间的空气间隙击穿电压,其主要决定于干闪络距离Ld,各闪络电压值与干闪络距离的关系如图9所示。上图表明套管空心复合绝缘子闪络电压随绝缘距离的增加而上升,且存在饱和效应。式(5)表明干闪络距离Ld与套管空心复合绝缘子闪络电压间的定量关系:

式中:Uf50为闪络电压值(放电概率为50%)/kV;Ld为绝缘子外部干闪络距离/m;A和B为待定系数。
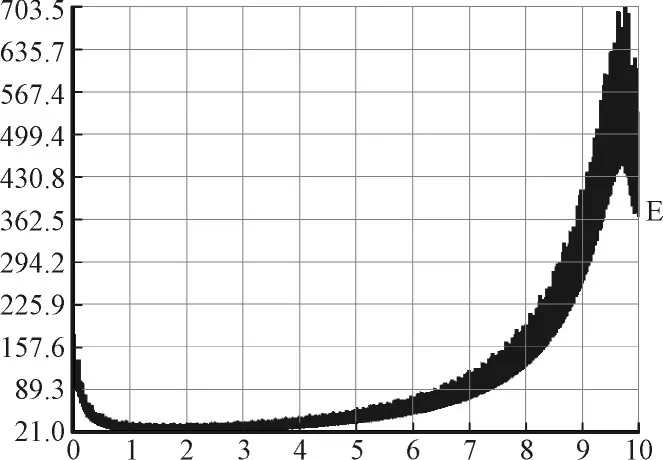
图7 户内端复合绝缘子表面电场分布Fig.7 Surface E-field distribution of indoor composite insulators

图8 户外端复合绝缘子表面电场分布Fig.8 E-field along the outdoor composite umbrella
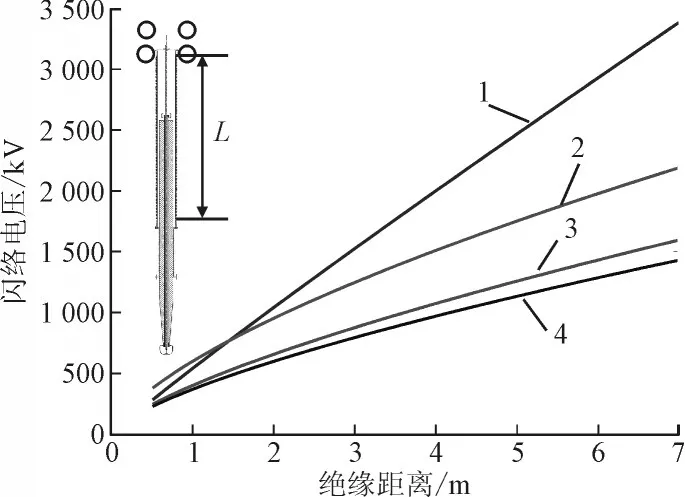
图9 标准大气压条件下空心复合绝缘子在空气中的闪络电压与绝缘距离的关系Fig.9 The relationship between flashover voltage and insulation distance of hollow composite insulator under standard atmospheric pressure
4.2 穿墙套管长空气间隙绝缘配置讨论
通过前面的分析可知,根据已有试验数据基本可定量计算闪络电压与绝缘距离间的定量关系。对图9中的曲线进行数值拟合如表2所示。

表2 复合绝缘子在空气中的闪络电压与绝缘距离间定量拟合关系Table 2 Quantitative relationship between flashover voltage and insulation distance of composite insulator
由于高压电极对接地体最小安全距离由操作电压控制,且空气间隙在负极性操作冲击下的放电电压远高于正极性冲击,因此主要讨论穿墙套管在正极性操作冲击放电特性试验讨论。结合表2及式(5)可知,正操作波干/湿闪络电压可通过式(6)表示:

式(6)来源为通过实体套管结构进行正操作波干/湿闪络电压开展冲击耐压试验,考虑到特高压电压等级条件下,穿墙套管体积大、长度长、重量大,直接应用实体套管进行操作冲击试验将存在较大困难,现仅讨论单纯均压罩对接地墙体或大地的放电情况。试验电压波形参数为250/2 500 μs,经过试验研究发现,不同空气间隙50%放电电压,标准冲击电压棒对板间隙的50%放电电压与间隙距离的关系,可近似由经验公式表示为[6]

对比式(6)和式(7),两式存在一定差异,将两者结果对比于图10中。特高压套管一般应用于高海拔地区,海拔修正系数可按推荐公式计算即

式中:H为海拔高度,m;q为指数,其取值根据不同电压类型进行选取。在2 300 kV操作冲击电压下,通过以上公式进行反演。从图10中可看出,在相同绝缘距离条件下,实体套管结构与简单金属电极相比较具有更高的闪络电压,原因在于实体套管结构具有更加均匀的电场分布。
为了更高的安全裕度,套管绝缘距离可设计为11m,其值可通过式(8)进行海拔修正。
5 结论
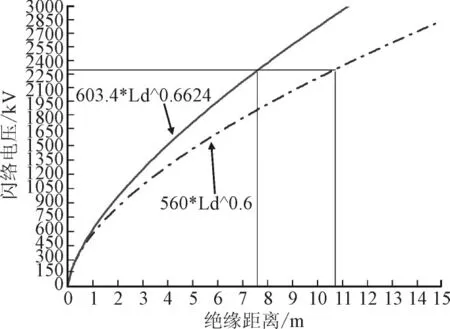
图10 不同试验条件下闪络电压与绝缘距离间的关系Fig.10 The relationship between flashover voltage and insulation distance under different test condition
分析了±800 kV特高压直流穿墙套管的运行环境,具备金属屏蔽的“U”型穿墙套管可用于±800 kV特高压穿墙套管的设计,有限元计算方法被用于特高压穿墙套管的三维电场分析,高场强区域主要集中在穿墙套管金属屏蔽和外均压环表面,其闪络电压和绝缘距离之间关系可通过式表征,穿墙套管的实际运行环境对其内外绝缘性能提出了更高的要求。
[1] 梁旭明,张平,常勇.高压直流输电技术现状及发展前景[J].电网技术,2012,36(4):1-9.
LIANG Xuming,ZHANG Ping,CHANG Yong.Recent ad⁃vances in high-voltage direct-current power transmission and its developing potential[J].Power System Technology,2012,36(4):1-9.
[2] 谢恒堃.电气绝缘结构设计原理:下册[M].北京:机械工业出版社,1992.
XIE Hengkun.Electrical insulation design principles[M].Beijing:Mechanical Industry Press,1992.
[3] 张学成,檀金华,牛万宇.±1 100 kV直流输电工程换流变压器阀侧套管的设计[J].高电压技术,2012,38(2):393-399.
ZHANG Xuecheng,TAN Jinhua,NIU Wanyu.Bushings design of converter transformer’s valve side of UHVDC transmission project[J].High Voltage Engineering,2012,38(2):393-399.
[4] 汤浩,申泽军,张书琦等.±1 100 kV特高压直流穿墙套管交、直流局部放电试验净空区域优化[J].高电压技术,2017,43(10):3173-3181.
TANG Hao,SHEN Zejun,ZHANG Shuqi,et al.Optimiza⁃tion of clearance test area for±1 100 kV UHVDC wall bush⁃ing in AC and DC partial discharge measurement[J].High Voltage Engineering,2017,43(10):3173-3181.
[5] 张良县,陈模生,彭宗仁,等.特高压换流变压器涡流损耗计算与屏蔽分析[J].变压器,2013,50(3):15-21.
ZHANG Liangxian,CHEN Mosheng,PENG Zongren,et al.Eddy current loss calculation and shield analysis of UHV converter transformer[J].TRANSFORMER,2013,50(3):15-21.
[6] 罗晓庆,胡伟,徐涛等.±1 100 kV直流U型结构穿墙套管空气间隙放电特性及间隙距离选择[J].高电压技术,2017,43(3):946-952.
LUO Xiaoqing,HU Wei,XU Tao,et al.Air gap flashover characteristics and selection of gap distances for±1 100 kV DC U-shaped wall bushing[J].High Voltage Engineering,2017,43(3):946-952.
[7]NATHAN D.JACOB,WILLIAM M.McDermid and Be⁃hzad Kordi.On-line Monitoring of Partial Discharges in a
HVDC Station Environment[J].IEEE Transaction on Mag⁃netics,2012,19(3):925-935.
[8]JASCHA L G,MATTHIAS C.KRANTZ,MARTINA Gerken.Two-Dimensional Versus Three-Dimensional Fi⁃nite-Element Method Simulations of Cantilever Magneto⁃electric Sensors[J].IEEE Transaction on Magnetics,2013,49(10):5287-5293.
[9] TANG L,RAGHUVEER M R.Modelling of HVDC Wall Bushing Flashover Due to Uneven Wetting[J].IEEE Trans⁃action on Power Delivery,1999,14(1):194-199.
[10]MONGA S,GORUR R S.Design optimization of high volt⁃age bushing using electric field computations[J].IEEE Transaction on Dielectrics and Electrical Insulation,2006,13(6):1217-1224.
[11]王晓琪,吴春风.1000kV GIS用套管的设计[J].高电压技术,2008,34(9):1792-1796.
WANGXiaoqi,WUChunfeng.Designof1000kVGISBush⁃ing[J].High Voltage Engineering,2008,34(9):1792-1796.
[12]党沙沙,许洋,张红松.ANSYS12.0多物理耦合场有限元分析入门到精通[M].北京:机械出版社,2010:254-311.
DANG Shasha,XU Yang,ZHANG Hongsong.ANSYS12.0 finite element analysis of multiphysics coupling field from start to master[M].Beijing:China Mechanical Press,2010:254-311.
