基于任务分解模型的离散数据格网化并行优化
2018-06-19王家润谢海峰
王家润,谢海峰
(华北计算技术研究所基础三部,北京 100083)
0 引 言
在国家“核高基”重大专项支持下,自主可控的软硬件发展迅速。但国产基础软硬件技术成熟度不高、技术储备不足、信息化生态环境不完善、体系化能力弱、整体安全性尚待提高等系列问题,还需要重点解决应用迁移、系统适配、性能优化等问题[1]。文献[1]针对典型基础软硬件,优化参数配置、语句性能、界面渲染、数据管理等;文献[2]通过综合运用并发处理、数据缓存、分片处理和分层显示等技术,对信息的产生、传输、处理、查询及显示的全过程进行性能优化;文献[3]研究了嵌入式环境中的国产化GPU JM5400对汉字的显示及大数据量图形的显示优化,但与商用相比,性能差距比较大。
基于CPU多核的OpenMP[4,5]及基于GPU的CUDA[5]的并行优化技术已在各领域中大量应用。文献[5]对现代处理器特性、串行代码优化、常用并行编程模型及设计方法等进行了深入分析;文献[6]研究了OpenMP在Kriging插值中的并行优化;文献[7]中将CUDA应用在运动目标检测处理;文献[8]研究了OpenMP在矢量空间数据拓扑算法中的并行优化;文献[9]研究了CUDA在电磁可视化中的性能加速;文献[10]研究了GPU性能优化的主要途径并提出了一个可视化的性能指导模型。上述研究针对不同的实际问题进行了并行优化,但是处理过程相对复杂、多样。
本文以离散数据格网化处理中的并行优化研究为例,研究国产应用性能提升技术。借鉴文献[10]的性能指导模型思想,针对并行编程中的线程任务划分这一共性难点,建立了一个用于指导任务划分的线程任务分解通用处理模型。
1 软硬件结合并行优化策略及处理流程
1.1 软硬件结合并行优化策略
国产CPU与商用相比虽然还存在差距,但因为普遍采用了多核技术,在一定程度上可弥补主频不足的问题;国产GPU目前没有面向桌面的产品,主要使用商用GPU,由于缺乏适配的驱动程序,只能采用开源的驱动程序替代,与商用性能差距较大,目前国产下GPU通用计算还无法实施。因此国产下性能优化应以国产CPU处理器提供的多核处理技术为主,以商用GPU为辅(主要用于对比验证及技术储备)。
1.2 软硬件结合并行优化处理流程
(1)性能分析
通过性能测试工具Intel VTune等找出软件中的性能瓶颈。
(2)并行处理
并行编程的思想是分治策略,即将大问题划分为一些小问题,再把这些小问题交给相应的处理单元并行处理。分解后的线程处理任务是否不相关(或相关性很低),这是并行优化的前提。
(3)对比验证
采用并行处理的软件,复杂性及调试难度较高,建议先采用串行编程,再并行优化,串行编程用于验证并行优化算法的正确性及性能优化对比。
(4)性能调优
根据CPU及GPU处理器硬件的结构特征,对并行优化过程中的细节调优(编译器选项、数据分块、内存使用、负载平衡、调度优化、缓存优化等[5,11,12])。
2 离散数据格网化IDW算法及并行优化设计
2.1 离散数据格网化IDW算法
离散数据格网化有广泛的应用,例如:气象观测站的分布是离散不规则的,需要先根据这些观测站数据来插值出规则网格点上的属性值(温度、气压等),基于规则网格,再采用等值线、填色图等进行可视化等。基于空间相近相似原理的反距离权重IDW插值算法是一种常用的方法。
反距离权重IDW插值算法[13]:
(1)输入
离散采样点数据(位置、属性等)集合;待插值规则网格的范围、行列数目等。
(2)过程
A:邻近搜索(Searching)
针对需要构建的规则网格中的每个格点,依据某种搜索规则,从离散采样点数据集合中搜索与该格点相距较近的若干个离散采样点,使用这些离散采样点插值计算该格点的属性值。目前有多种搜索规则:圆域、四方向、八方向、基于Delaunay三角网一阶邻近点、基于遮蔽程度的搜索等[13-15],本文采用四方向搜索法。
B:插值计算(Computing)
针对规则网格中的每个格点搜索出的若干个离散采样点,采用反距离权重IDW插值公式对这若干个离散采样点属性数据进行计算,得到该网格格点的属性值。IDW插值计算公式
其中,权重系数
其中,Z(S0)为S0处的预测值,N为计算过程中使用的邻近采样点数量,Zi为第i个采样点的值,di为插值点S0到各采样点的距离,2是距离的幂。
(3)输出
插值计算出的各网格的格点属性值。根据需要可进一步进行交叉验证,计算插值误差等。
由IDW插值算法过程可知,规则格网的格点数目一般比较大、计算密集,每个格点的搜索及插值与邻近的格点没有依赖,相互独立,非常符合并行化处理。下面遵循软硬件结合的并行优化策略,进行并行优化。
2.2 基于OpenMP的并行优化PIDW算法
OpenMP使用Fork-Join并行编程模型,程序创建一个独立的串行执行的主线程,执行到OpenMP标识的并行域时,即进入Fork过程:主线程会根据任务的划分创建一组并行的子线程,然后并行域中的程序代码在不同的线程中并行执行;Join过程:当主线程创建的并行子线程在并行域中执行完任务,退出并行域时,OpenMP内部同步各子线程,结束各子线程,返回到只有主线程运行状态。
基于Fork-Join并行编程模型的并行优化PIDW算法:
(1)输入
待插值网格格点数据、离散采样点数据、网格范围及行列数目等。
(2)过程
步骤1 设置OpenMP运行参数:获取CPU核数,根据核数设置要启动的子线程数。设置子线程数目与核数相同,可最大程度上利用各核提供的硬件能力,使各核具有较好的负载均衡。
步骤2 进入OpenMP并行域(Fork):根据子线程数目进行任务划分,确定每个线程负责的任务。子线程计算网格格点的属性值(搜索邻近采样点,并采用IDW插值公式计算)。各子线程间的计算相对独立,互不干扰。详细可参见基于OpenMP的线程任务分解模型部分。
步骤3 退出OpenMP并行域(Join):OpenMP并行域执行完毕后,即结束并行计算模式,此时网格格点数据插值处理完毕。
(3)输出
经过插值处理的网格格点数据。
基于OpenMP实现的代码示例:
//gridData:待插值网格格点数据,待插值网格列
//数、行数:gridNumX,girdNumY
//离散采样点数据:sampleData
//获取CPU处理器的核数目
intthreads=omp_get_Num_threads();
//设置并行启用threads个子线程,启用CPU所有//核
omp_set_threads(threads);
//进入并行域(Fork),启用threads个子线程
//各线程相互独立,并行处理计算任务
#pragmaompparallel//OpenMP并行域标识
{
//获取当前子线程索引,索引范围:0~threads-1
intthreadIdx=omp_get_thread_num();
//设置该子线程的循环计算任务:不越界
//(i //(i+=threads),不重复且保证所有的线程计算 //覆盖所有的网格格点计算 for(inti=threadIdx;i for(intj=0;j //搜索与插值计算 SearchCompute(i,j,gridData, gridNumX,gridNumY,sampleData); }//退出并行域,结束threads个子线程,返回主线 //程(Join),此时网格gridData的各格点数据已 //经过插值处理,可用等值线跟踪算法等进一步处//理,可视化显示等。 OpenMP总共分配有N个子线程(在整个并行处理域内,OpenMP会为每个子线程分配唯一的索引threadIdx,索引号范围:0~N-1),需要处理columnNum列、rowNum行的二维网格格点的计算任务(网格格点从左下角(0,0)开始,沿X、Y方向编号)。 在一般情况下,子线程数目远远小于网格格点数目,因此,每个子线程需要负责多个格点的计算。基本划分思想是将网格格点按列(或行)分解到N个组中,每个组由一个子线程负责计算,重点是建立线程索引与网格格点索引的映射关系,下面通过二重循环来完成每个子线程的任务分解: intthreadIdx=omp_get_thread_num(); for(inti=threadIdx;i for(intj=0;j GridNodeCompute(…); 即针对并行域中的当前线程threadIdx,由该线程负责处理网格中从第i=threadIdx列(即将线程索引threadIdx映射到网格的第i列)开始到columnNum-1列范围内的各列格点的所有计算(j:0~rowNum),其中列i的递增间隔为线程总数N,原因是已分配有N个线程,前0~N-1列已分配到这N个子线程中并行处理,所以前N列无需重复计算,这是线程并行任务划分的关键。i=i+N表示沿X方向继续搜寻需要该线程计算的列,保证计算不遗漏。i 线程任务分解模型如图1所示,共使用4个子线程:0~3,将网格中的前4列直接映射到4个线程(图中左侧细线矩形范围内的4列网格格点),其中线程0负责网格的列0与列4格点计算(参见圆符号标记),线程1、2与线程0处理类似,线程3只处理网格列3(参见矩形符号标记)。 图1 基于OpenMP的线程任务分解模型 线程任务分解模型的计算均衡(负载平衡):一般情况下,首先每个线程参与计算,对应使用了CPU的各核,对计算任务进行了基于全部核的分解;其次,通过任务分解模型示意图可看出,各线程之间最多相差网格的一列或一行格点,各线程的计算量相差不太大,整体来说,计算比较均衡,即线程任务分解模型具有较好的负载均衡。 根据CUDA架构的编程模型(HostDevice)[5],基于CUDA的并行计算主要分为以下3个过程:将待处理数据由Host端(CPU)读入Device端(GPU)显存中;在Device端(GPU)中,进行并行计算:采用多线程并行处理数据,并将处理结果存储在显存中;把Device端(GPU)中的处理过的数据读回Host端(CPU)的内存中。CUDA内核函数运行在GPU上,启动后CUDA中的每一个线程都将会同时并行地执行内核函数中的代码。GPU是由多个流多处理器构成,以块(Block)为基本调度单元,因此对于流处理器较多的GPU,一次可以处理的块(Block)更多,从而运算速度更快。 使用CUDA编程主要注意:①线程的设置。获取GPU硬件参数:流处理器及线程块最大线程个数等参数及处理问题规模等。②线程的索引标识。每个线程都有线程索引threadIdx、所在的块索引blockIdx、所在块的维数blockDim、所在的线程网格维数gridDim等CUDA内置的信息(图2),通过这些信息可计算出线程在整个线程网格Grid中的索引位置,如在线程网格的X索引方向的索引位置 threadIdx.x+blockIdx.x*blockDim.x 基于CUDA架构编程模型的并行优化PIDW算法: (1)输入 待插值网格格点数据、离散采样点数据、网格范围及行列数目等。 (2)过程 步骤1 获取GPU设备的硬件参数:GPU的流处理器(SP)个数、线程块的最大线程数量等。 步骤2 根据GPU设备参数及网格格点数据维数(columnNum,rowNum),设置CUDA中线程网格的划分gridDim;线程块的划分blockDim,这样在CUDA中分配的总线程数:gridDim.x*gridDim.y*;blockDim.x*blockDim.y。 因为不同的GPU硬件的限制及网格数据规模等的限制,网格及块划分要根据实际环境调整。gridDim及blockDim的划分有多种方式,本文采用二维形式的gridDim及blockDim为例。一种常用的划分如下:gridDim(ceil(columnNum/16),ceil(rowNum/16));blockDim(16,16),其中ceil取上限整数。 步骤3 在显存(GPU)和内存(CPU)中为待插值网格格点属性数据开辟存储空间,在显存中为离散采样点数据开辟存储空间,将离散采样点的数据由内存拷贝到显存。 步骤4 根据CUDA中设置的线程数和任务量进行任务划分,指定每个线程负责的任务。各线程计算网格格点的属性值(搜索邻近采样点,并采用IDW插值公式计算)。各线程间的计算相对独立,互不干扰。详细参见基于CUDA的线程任务分解模型。 步骤5 启动并行计算模式(即CPU端启动核函数),在GPU端由GPU中的多个线程并行计算网格格点的属性值。 步骤6 结束并行计算模式(即GPU端核函数结束,返回CPU端),将网格格点数据由显存(GPU)拷贝到内存(CPU)[11,12]。 (3)输出 输出已插值计算的网格格点数据。 CUDA部分实现示例代码: //gridData:待插值网格格点数据,待插值网格行//数、列数:gridNumX,girdNumY //离散采样点数据:sampleData //核函数 GridingParalleComputing<< //核函数类似OpenMP中并行域概念 { //设置为二维线程网格,当前线程索引CUDA内部 //采用二维(threadIdx.x,threadIdx.y)标识, //所在的线程块由(blockIdx.x,blockIdx.y)标 //识 intI=threadIdx.x+blockIdx.x*blockDim.x; intJ=threadIdx.y+blockIdx.y*blockDim.y; //该线程的任务分解:不越界(i //j //i+=gridDim.x*blockDim.x及 //j+=gridDim.y*blockDim.y,类似OpenMP中的 //计算任务处理 for(inti=I; i i+=gridDim.x*blockDim.x) for(intj=J; j j+=gridDim.y*blockDim.y) //搜索与计算 SearchCompute(i,j,gridData, gridNumX,gridNumY, sampleData); } 网格格点数据维数(columnNum,rowNum),采用二维形式的gridDim及blockDim,CUDA总共分配有threads=gridDim.x*gridDim.y*blockDim.x*blockDim.y个线程。基本划分思想是将网格格点分解到threads个组中,每个组由一个线程负责计算,重点是建立线程索引与网格格点索引的映射关系。在每个块内,CUDA会为每个线程分配唯一的索引threadIdx(threadIdx.x,threadIdx.y),因为采用二维形式的blockDim,所以threadIdx也取二维形式。需要处理columnNum列、rowNum行的网格格点的计算任务(网格格点从左下角(0,0)开始编号),通过二重循环来完成线程的任务分解: intcol=threadIdx.x+ blockIdx.x*blockDim.x; introw=threadIdx.y+ blockIdx.y*blockDim.y; for(inti=col; i i+=gridDim.x*blockDim.x) for(intj=threadIdx.y; j j+=gridDim.y*blockDim.y) GridNodeCompute(…); 每个线程相对于所在的线程块,有唯一索引,则在整个线程网格中的索引为:(col,row)=(threadIdx.x+blo-ckIdx.x*blockDim.x,threadIdx.y+blockIdx.y*blockDim.y); 即针对块中的线程threadIdx,由该线程负责处理对应的网格数据中的col列、row行索引格点的计算(如果col列、row行格点存在)。从第i=col列、第j=row行开始到columnNum-1列、rowNum-1行范围内的各格点的所有计算,其中列i的递增间隔为gridDim.x*blockDim.x,其中行j的递增间隔为gridDim.y*blockDim.y,原因是已分配有threads个线程,其中:x方向间隔gridDim.x*blockDim.x;y方向间隔gridDim.y*blockDim.y。网格数据的前0~gridDim.x*blockDim.x-1列及0~gridDim.y*blockDim.y-1行已映射到threads个线程中并行处理,所以无需重复计算,这是线程并行划分的关键。i+=gridDim.x*blockDim.x与j+=gridDim.y*blockDim.y表示继续沿x、y两个方向搜索该线程负责计算的格点,主要保证计算不遗漏。i 线程任务分解模型如图3所示,其中gridDim(3,2),blockDim(2,2),共分配线程个数:24个,直接映射到网格格点(图中左下方细线矩形范围内的24个网格格点),线程网格索引(0,0)(参见菱形符号标记),所在的块索引block(0,0)及该块中线程索引thread(0,0),分配的计算任务是计算网格格点(0,0)、(6,0)、(0,4)、(6,4);线程网格索引(5,2)(参见三角符号标记),所在的块索引block(2,1)及该块中线程索引thread(1,0),分配的计算任务是计算网格格点(5,2)、(5,6)。 图3 基于CUDA的线程任务分解模型 线程任务分解模型的计算均衡(负载平衡):一般情况下,首先GPU分配的所有线程参与计算,对计算任务进行了基于全部线程的分解;其次,通过任务分解模型示意图可看出,各线程处理的格点在二维网格上均匀间隔分布,整体来说,计算比较均衡,即线程任务分解模型具有较好的负载均衡。 采用传统的串行算法(CPU单核)、并行算法(CPU多核OpenMP)、并行算法(GPU多核CUDA)3种方式,统计总消耗时间、加速比(串行算法时间/并行算法时间之比)等。 实验数据选自全球气象观测709个站点,地理范围:经度-180°~180°,维度-90°~90°,数据网格以360×180为基准(即经纬度按1°划分),采用网格系数表达网格疏密程度,例如网格系数为2,表示360×2×180×2。 (1)实验环境:国产麒麟Kylin操作系统(32位),CPU:申威(SW410)、龙芯(Loongson3A2000)、英特尔(Intel I5),均为四核。 (2)实验结果:统计消耗时间及加速比,并绘制成曲线图,结果参见表1、表2、图4~图7。 表1 网格系数2时多核并行加速性能测试统计 表2 网格系数4时多核并行加速性能测试统计 图4 网格系数2时CPU消耗时间对比 图5 网格系数2时CPU加速比曲线 图6 网格系数4时CPU消耗时间对比 图7 网格系数4时CPU加速比曲线 (3)实验分析:选取3种CPU及两种网格划分,对IDW算法并行实验,从表格及曲线图可看出: 加速比:经过并行加速后,加速比达到3.75~5.614。龙芯(最大加速比3.82)及申威CPU(最大加速比3.75)接近4倍,这二者基本相当,英特尔CPU超过4倍(最大加速比5.614),加速比最高。 总消耗时间:经过并行加速后,消耗时间大量减少。龙芯与申威二者基本相当,英特尔消耗最少:6.883。 基本结论:采用OpenMP并行优化IDW算法是有效的,整体加速比基本符合与CPU的核数相当这一经验值,也说明了OpenMP加速受CPU核心数的限制。从加速比可看出,国产与商用CPU存在差距。 (1)实验环境:CPU:Intel I2,双核;GPU:NVIDIA Quadro 240;操作系统:windows XP 32位;CUDA Cores:16个;CUDA v6.5。 (2)实验结果:统计消耗时间及加速比,并绘制成曲线图,结果参见表3、图8、图9。 (3)实验分析:通过采用不同疏密网格划分,在Windows操作系统下对IDW算法并行优化实验,从表格及曲线图可看出: 加速比:加速比在1.9~5.9之间,性能提升显著。随着网格数据量的增加,加速比更高,可看出GPU比较适合大规模的数据并行计算。 表3 GPU并行加速性能测试统计 图8 GPU加速前后消耗时间对比 图9 GPU加速比曲线 总消耗时间:经过GPU并行加速后,优化后消耗时间比优化前消耗的时间大量减少。针对网格系数4,比较表2与表3消耗时间(Intel I5:34.352, GPU:20.187),可看出CUDA比OpenMP更有效。 基本结论:采用CUDA并行优化IDW算法更加有效。 基于OpenMP与CUDA的并行优化,具有较好的性能提升。将本文并行优化技术应用到国产下某型号气象业务系统项目中,该应用系统性能得到较大的改善,效果如图10所示。 图10 局部区域等值线显示效果 针对传统的IDW算法采用并行优化处理后,实现了较好的性能提升,体现了CPUGPU多核的硬件加速能力,验证了软硬件结合并行优化思路的正确性,线程任务分解模型也极大地减轻了并行编程任务划分的难度,为国产软件的性能提升提供了一定的指导。下一步可研究:①目前CUDA仅支持NVIDIA显卡,支持多种显卡的OpenCL通用计算技术;②基于Hadoop MapReduce、Spark等分布式大规模数据的并行计算技术;③针对OpenMP及CUDA的性能优化。 参考文献: [1]ZHANG Xiaoqing,GONG Bo,TIAN Liyun,et al.Study on the performance optimization of application running on the platform built with Chinese owned technology[J].Software,2015,36(2):5-9(in Chinese).[张晓清,龚波,田丽韫,等.国产自主可控应用性能优化研究[J].软件,2015,36(2):5-9.] [2]XIE Zhouyu,ZANG Fei.Performance optimization technology for information system based on domestic software and hardware[J].Command Information System and Technology,2014,5(3):59-63(in Chinese).[谢宙宇,臧飞.基于国产软硬件的信息系统性能优化技术[J].指挥信息系统与技术,2014,5(3):59-63.] [3]FU He,XIE Yongfang.From design of a cockpit display system based on homemade GPU JM5400[J].Computer Engineering & Science,2016,38(10):2083-2090(in Chinese).[符鹤,谢永芳.基于国产化图形芯片JM5400的座舱显示系统设计[J].计算机工程与科学,2016,38(10):2083-2090.] [4]OpenMPI[EB/OL].[2017-04-07].http://www.open-mpi.org. [5]LIU Wenzhi.Parallel computing and performance optimization[M].Beijing:China Machine Press,2015:2-174(in Chinese).[刘文志.并行算法设计与性能优化[M].北京:机械工业出版社,2015:2-174.] [6]CHEN Huan,XIE Jian.Kriging interpolation algorithm based on OpenMP[J].Computer Science,2012,39(6A):392-394(in Chinese).[陈欢,谢健.基于OpenMP的Kriging插值算法研究[J].计算机科学,2012,39(6A):392-394.] [7]LING Bin.DENG Yan.YU Shibo.Processing for accelerated sparse PCNN moving target detection algorithm with CUDA[J].Computer Engineering and Design,2016,37(12):3301-3305(in Chinese).[凌滨,邓艳,于士博.CUDA并行加速的稀疏PCNN运动目标检测算法[J].计算机工程与设计,2016,37(12):3301-3305.] [8]GU Yuhang,ZHAO Wei,LI Li,et al.Design and realization of parallel topology algorithm of vector spatial data based on OpenMP[J].Engineering of Surveying and Mapping,2015,24(11):22-27(in Chinese).[谷宇航,赵伟,李力,等.基于OpenMP的矢量空间数据并行拓扑算法设计与实现[J].测绘工程,2015,24(11):22-27.] [9]WU Lingda,HAO Liyun,FENG Xiaomeng,et al.Combining isosurface rendering and volume rendering for method of electromagnetic environment visualization[J].Journal of Beijing University of Aeronautics and Astronautics,2017,43(5):887-893(in Chinese).[吴玲达,郝利云,冯晓萌,等.结合等值面绘制与体绘制的电磁环境可视化方法[J].北京航空航天大学学报,2017,43(5):887-893.] [10]JIA Haipeng.Research of parallel optimization technologies on GPU computing platforms[D].Qingdao:Ocean University of China,2012:1-105(in Chinese).[贾海鹏.面向GPU计算平台的若干并行优化关键技术研究[D].青岛:中国海洋大学,2012:1-105.] [11]DAI Chen,CHEN Peng,YANG Donglei,et al.On parallel programming and optimization for multi-core[J].Computer Application and Software,2013,30(12):198-202(in Chinese).[戴晨,陈鹏,杨冬蕾,等.面向多核的并行编程和优化研究[J].计算机应用与软件,2013,30(12):198-202.] [12]SHAO Tianjiao.Research on GPU-based parallel computation performance optimization[D].Changchun:Jilin University,2014:1-48(in Chinese).[邵天骄.基于GPU并行计算的性能优化研究[D].长春:吉林大学,2014:1-48.] [13]ZHOU Hongwen,DU Yuxing,REN Gaofeng,et al.Analysis of ore reserves based on Arc-Engine and IDW[J].Journal of Wuhan University of Technology,2014,36(2):115-119(in Chinese).[周洪文,杜玉星,任高峰,等.基于Arc-Engine与IDW法的矿石储量分析研究[J].武汉理工大学学报,2014,36(2):115-119.] [14]DUAN Ping,SHENG Yehua,LI Jia,et al.Adaptive IDW interpolation method and its application in the temperature field[J].Geographical Research,2014,33(8):1417-1426(in Chinese).[段平,盛业华,李佳,等.自适应的IDW插值方法及其在气温场中的应用[J].地理研究,2014,33(8):1417-1426.] [15]LI Zhengquan,WU Yaoxiang.Inverse distance weighted interpolation involving position shading[J].Acta Geodaetica et Cartographica Sinica,2015,44(1):91-98 (in Chinese).[李正泉,吴尧祥.顾及方向遮蔽性的反距离权重插值法[J].测绘学报,2015,44(1):91-98.]2.3 基于OpenMP的线程任务分解模型
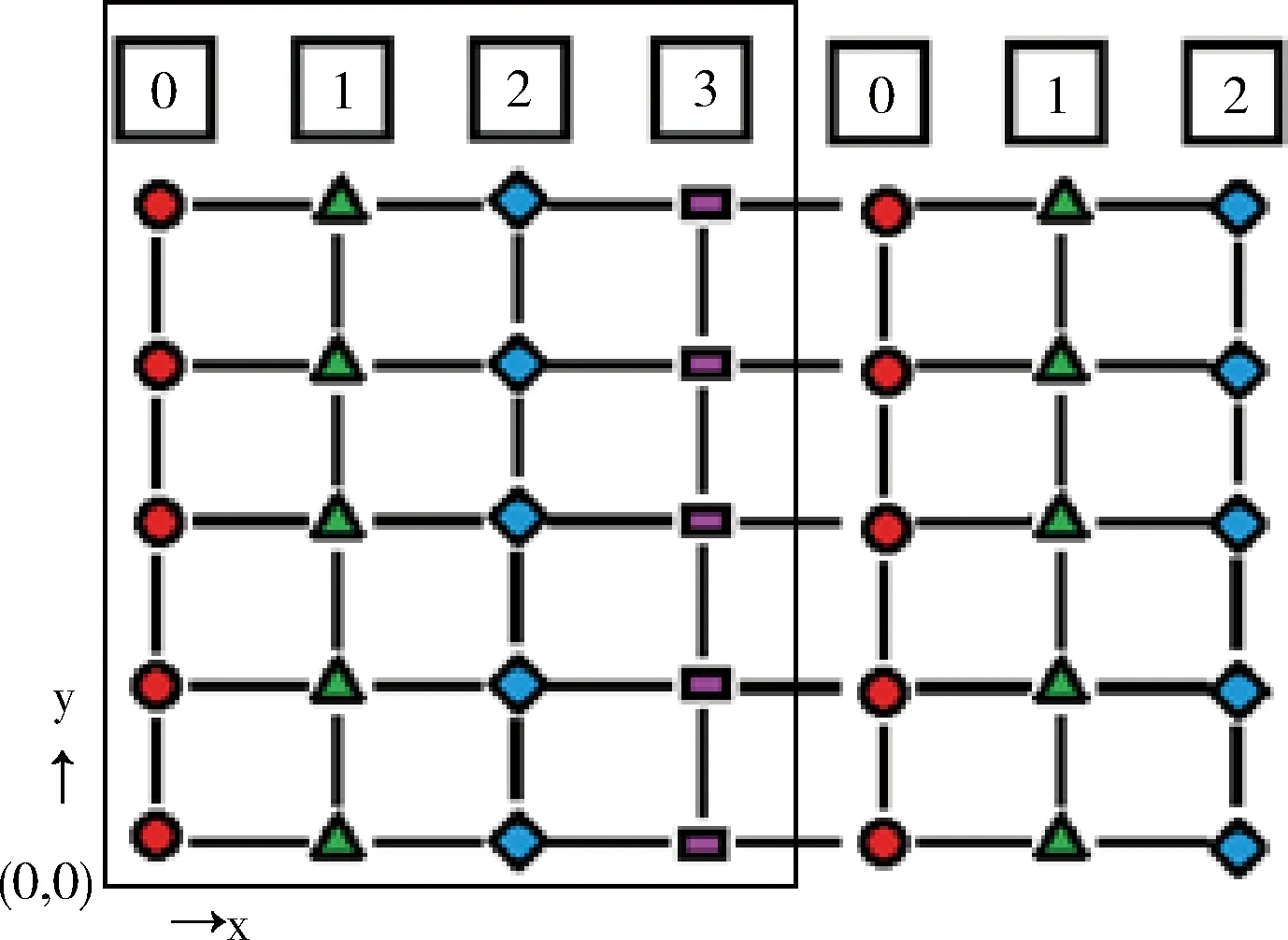
2.4 基于CUDA的并行优化PIDW算法
2.5 基于CUDA的线程任务分解模型
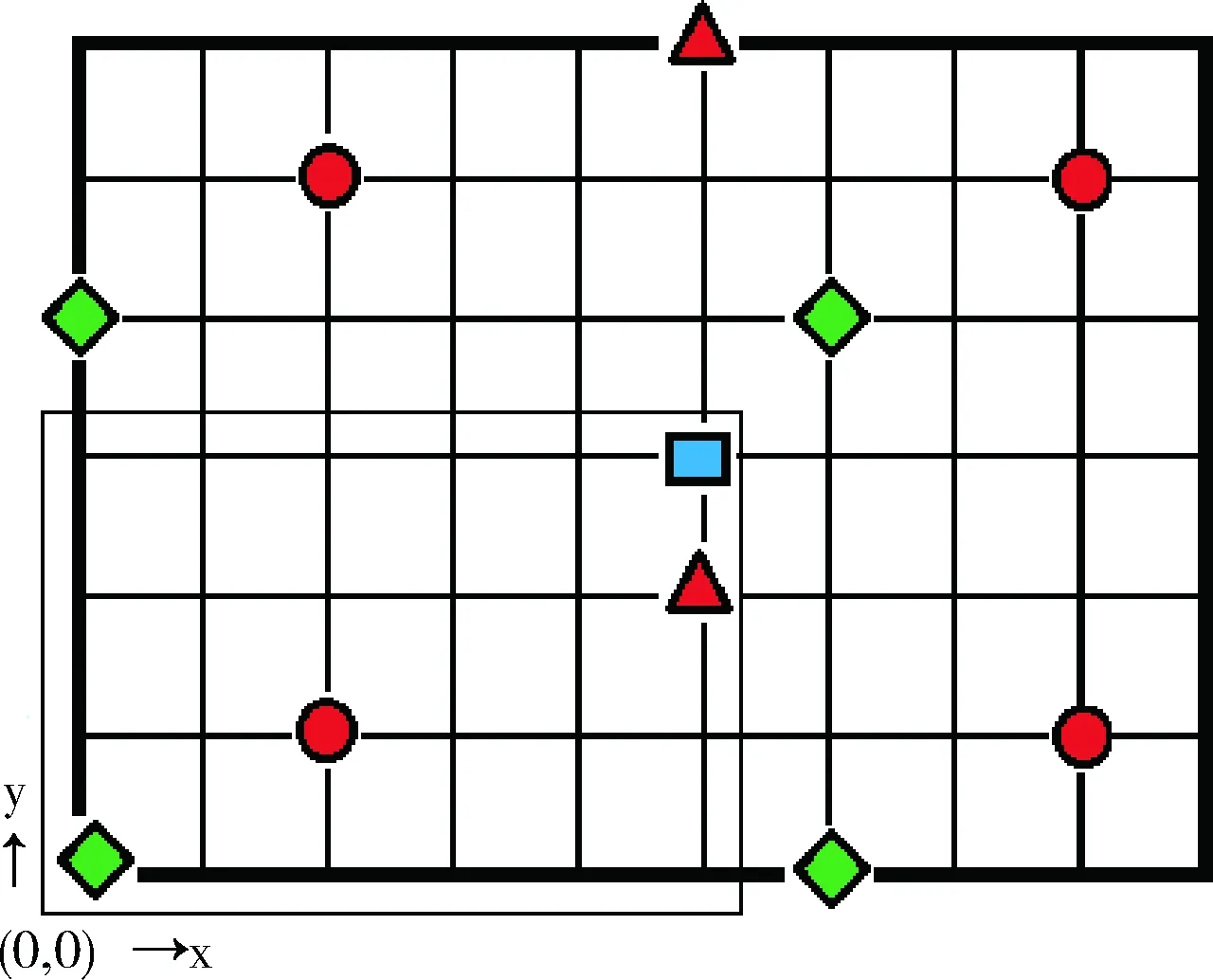
3 算法实验
3.1 实验一、OpenMP并行优化及分析
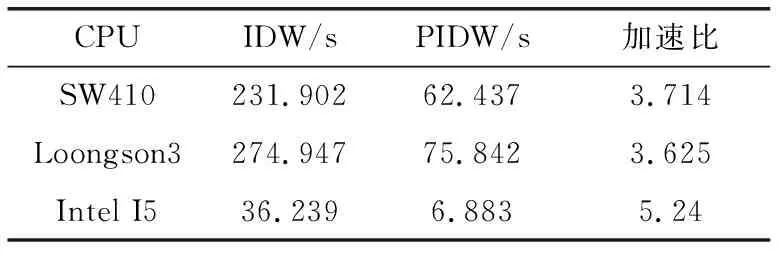

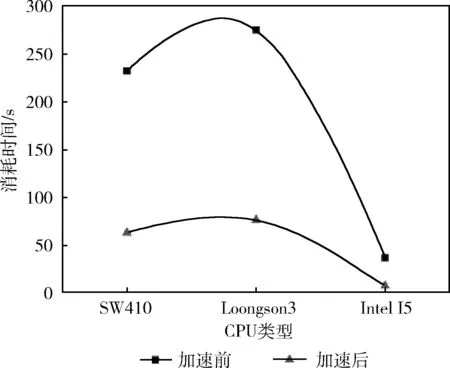
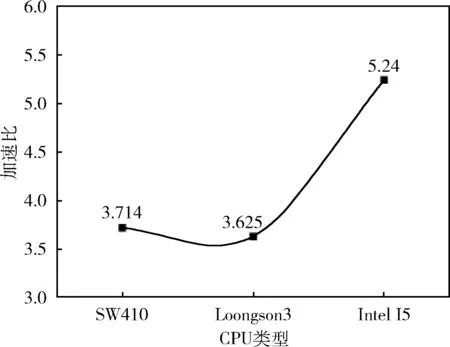
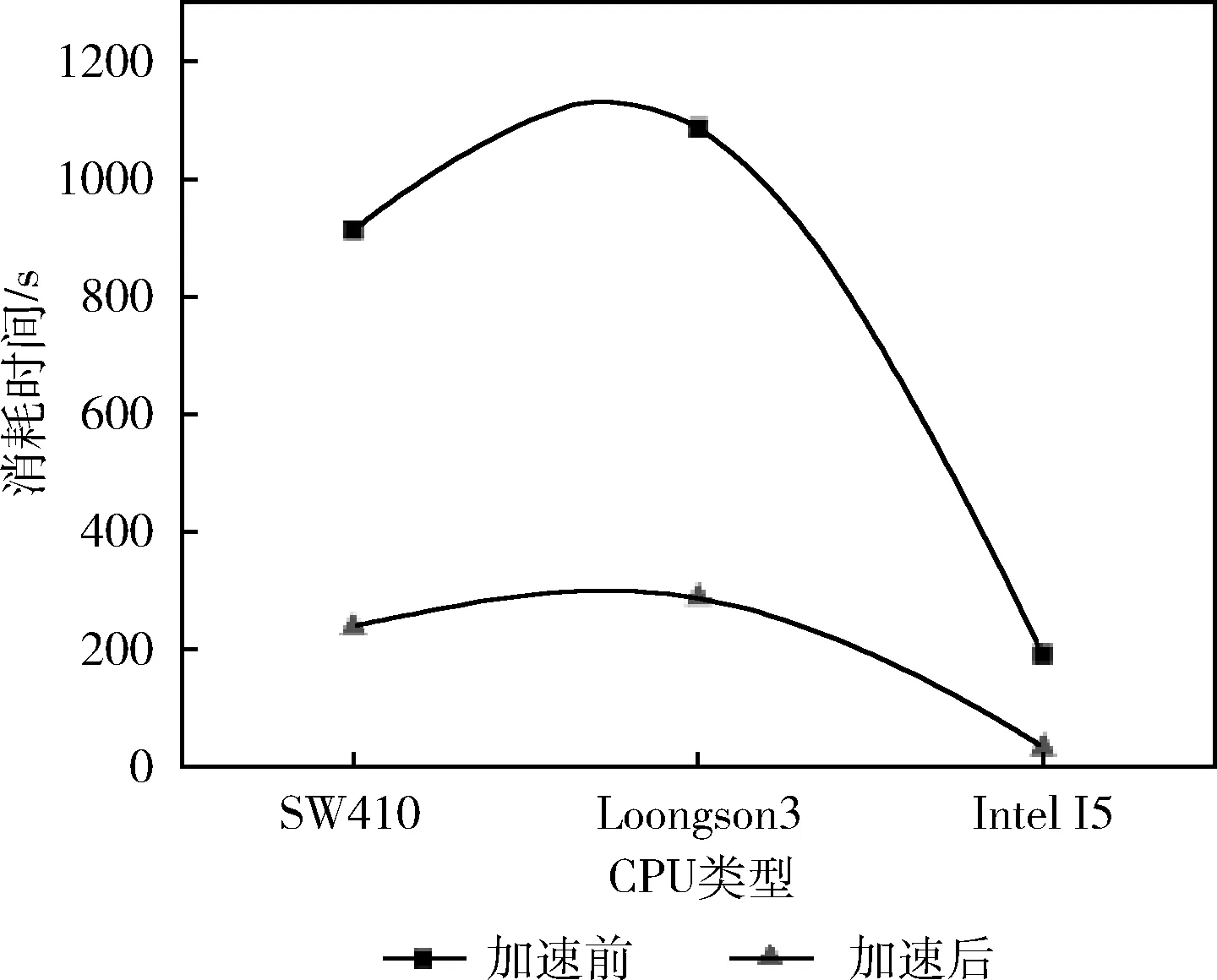
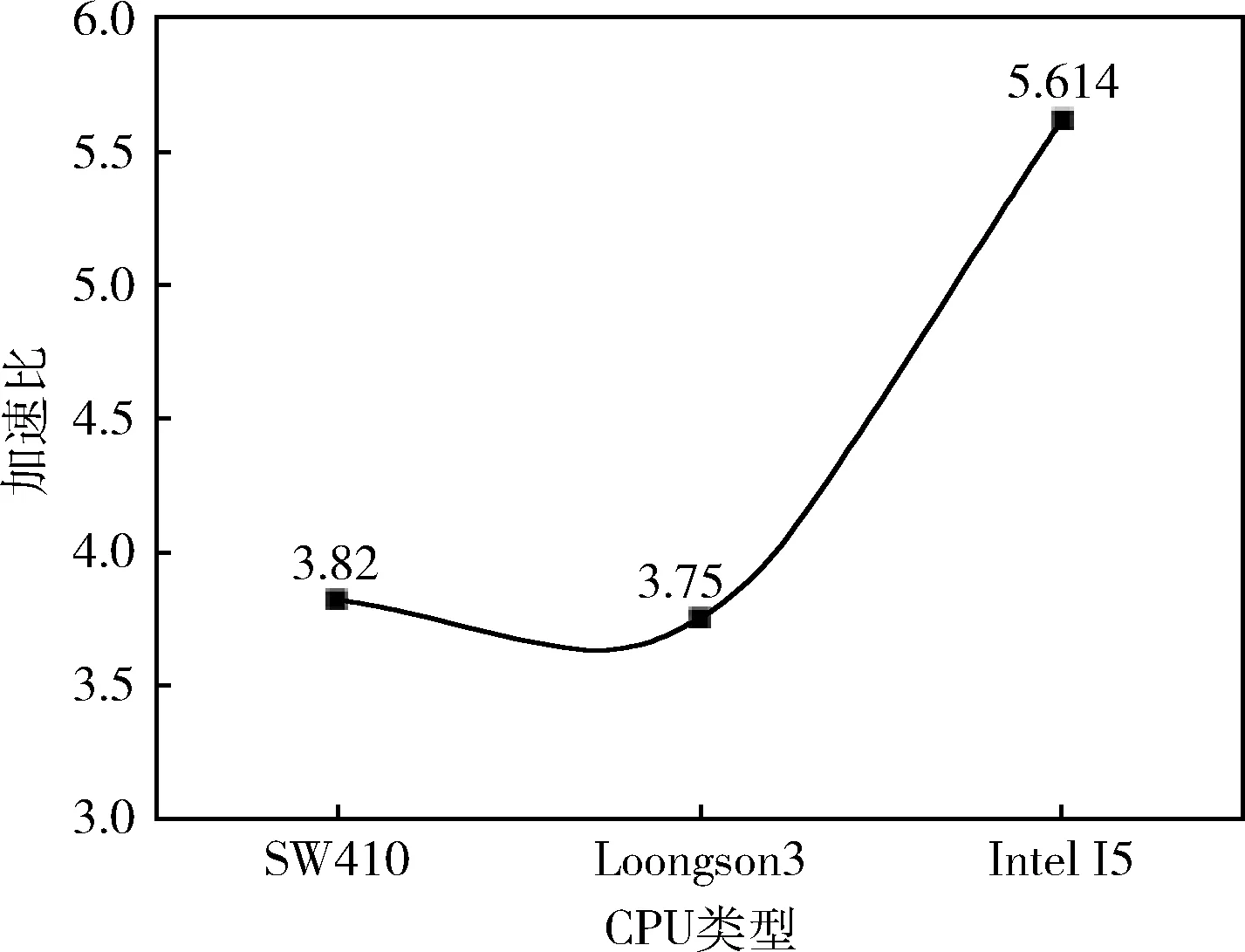
3.2 实验二、CUDA并行优化及分析
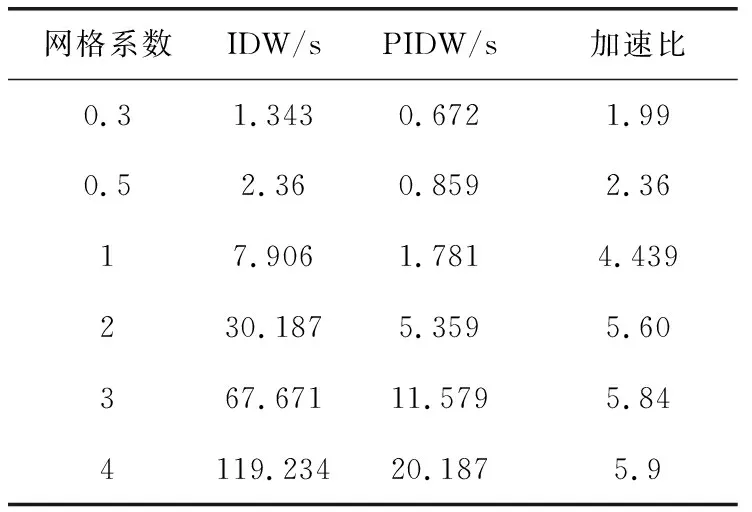
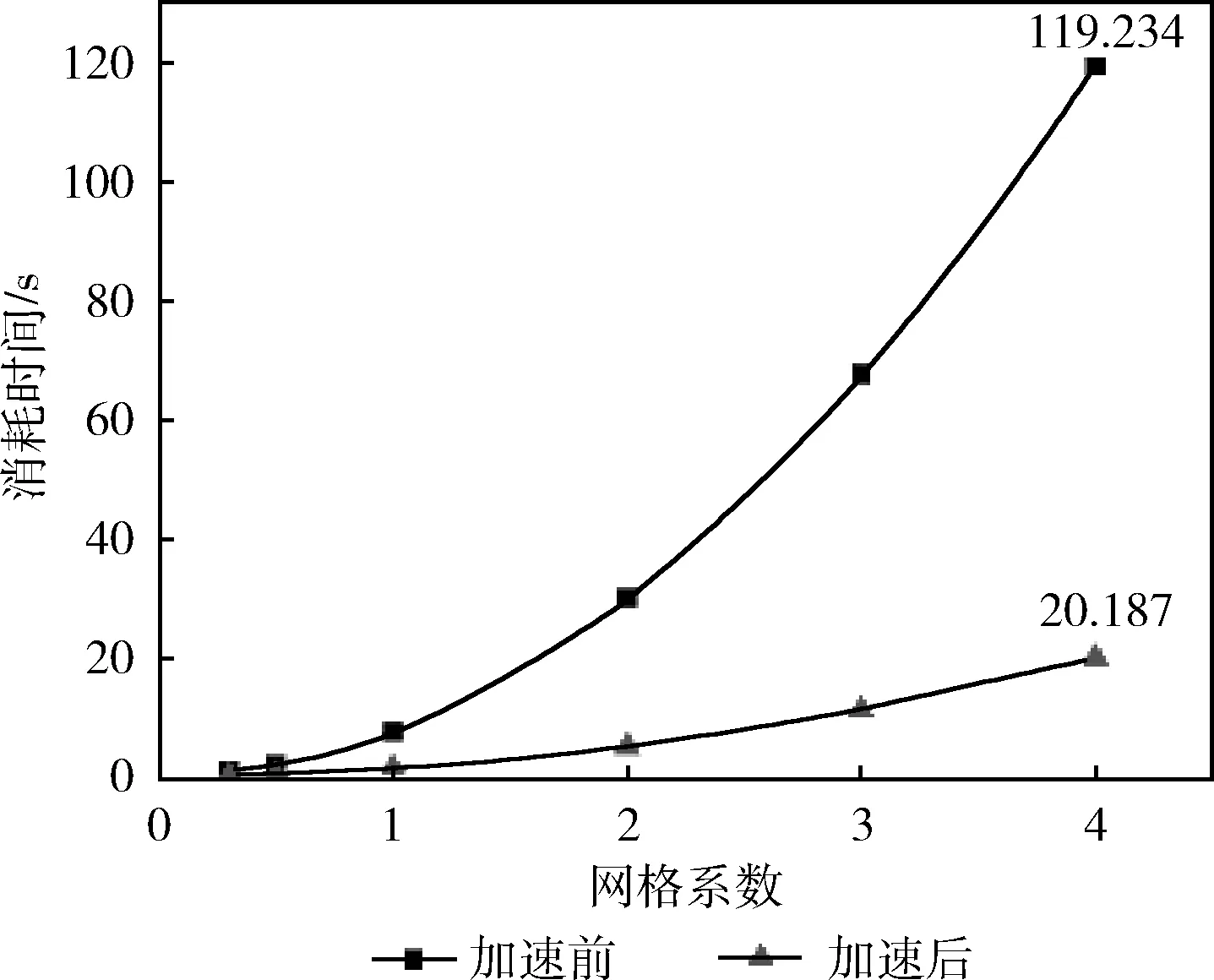
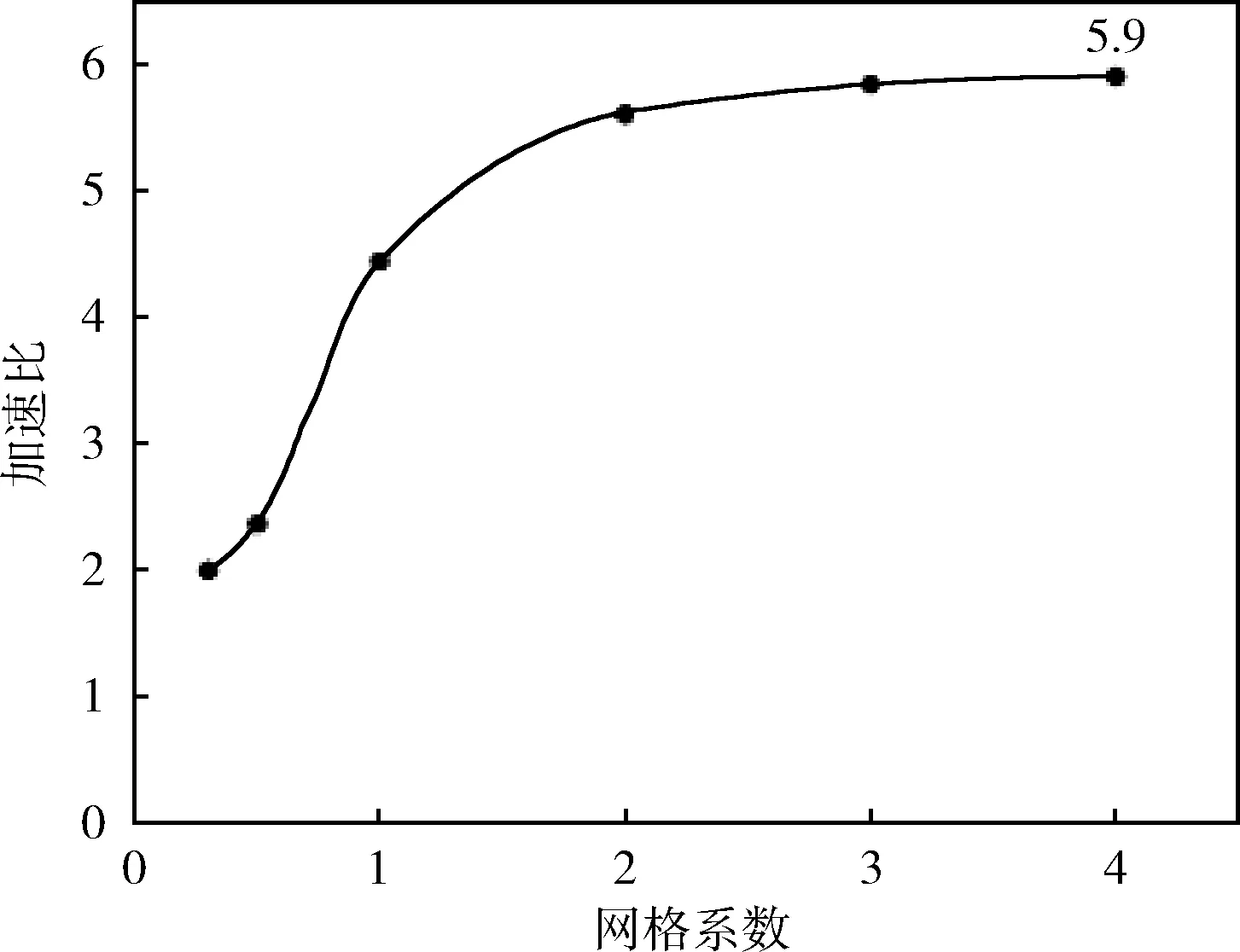
3.3 结论及应用效果

4 结束语
