二维分数阶泰勒级数算法在边缘检测中应用
2018-06-19李忠海宋智钦王崇瑶
李忠海,宋智钦,王崇瑶
(沈阳航空航天大学 自动化学院,辽宁 沈阳 110136)
0 引 言
分数阶微分可以使图像的高频变化特性信息清晰展现的同时,还能非线性地保留具有中、低频变化特性的信息,这个优势逐渐成为众多学者的研究热点[1-4]。Mekideche等[5]提出了FIM算法,该算法引入了分数阶积分掩模,且缩减运算时间;甘志凤等[6]根据数字图像的自相关性对R-L分数阶微分中常数分数阶微分不为0的情况进行改进;勾荣等[7]在改进分数阶微分G-L定义的基础上,提出了5×5的分数阶微分算子;何春等[8]利用分数阶微分和积分组成的复合导数提出了一种基于复合导数的边缘检测算子;田丹等[9]将分数阶微分与Sobel算子结合起来,构建了一个分数阶权矩阵Sobel算子;蒋伟等[10]将分数阶微分理论与Sobel算子相结合,提出了一种基于分数阶微分的Sobel算子。虽然分数阶微分在图像处理中的应用越来越多,但如何准确有效的将图像边缘的各种细节信息充分提取且又清晰展现的研究少之又少。
本文将G-L(Grünwald-Letnikov)分数阶微分、泰勒公式和二维整数阶微分相结合,推出了二维分数阶泰勒级数函数式;之后推算出分数阶微分的方向系数,并将此与Sobel算子相结合,从而构建二维分数阶泰勒级数Sobel算子。实验结果表明,该算子充分利用所检测像素点的邻近像素信息,能够将图像边缘中丰富的纹理细节充分提取,并获得一定的增强效果。
1 图像分数阶微分特性的信号处理分析
1.1 分数阶微分阶次的确定
对平方可积信号f(t)∈L2(R),其任意分数阶微分Dαf(r)频域形式可表示为
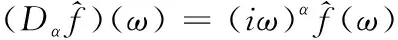
(1)
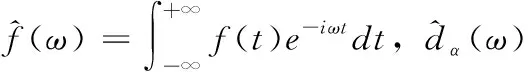
(2)
通过上面分数阶从时域向频域的推导发现,分数阶的作用是对信号的相位进行相应调整,由式(1)和式(2)可绘制出分数阶微分各阶次的幅频特性曲线,如图1所示。
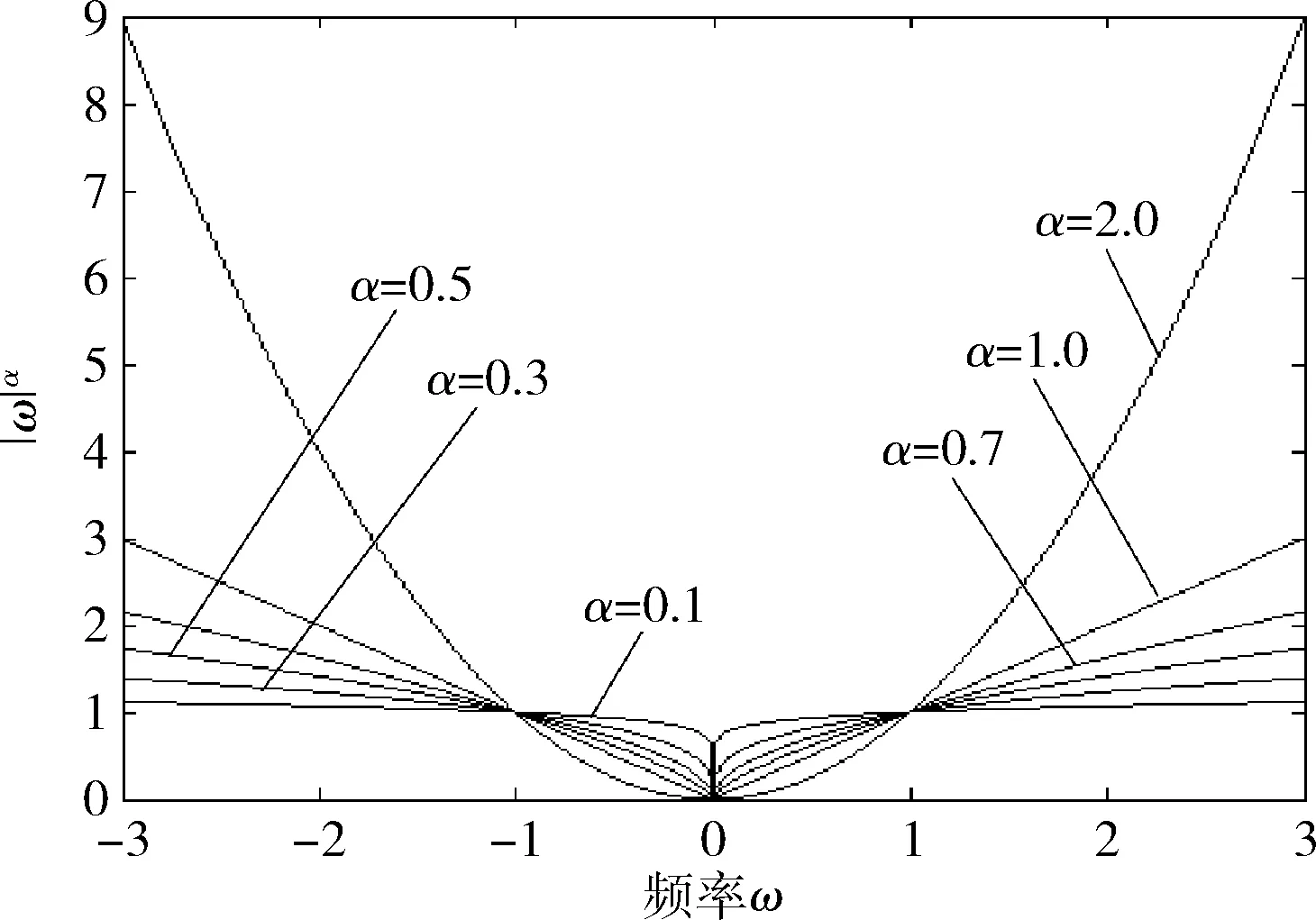
图1 分数阶微分对信号的幅频特性曲线
从图1中可看出[11]:分数阶微分的阶次范围在α∈(0,1)时,对于低频信号有较大程度的非线性保留,对于中频信号有较大幅度的增强,对于高频信号也有较大程度的提升。由此对于边缘细节信息较丰富的图像在α∈(0,1)内的分数阶微分阶次能够较大程度地检测图像感兴趣区域的边缘,使感兴趣区域的纹理细节信息较大程度的保留。
1.2 二维分数阶微分用于图像边缘提取的分析
图像一般被认为是信号在图像域中的另一种体现形式,因此分数阶微分算子也能运用于图像领域。边缘检测在现实情况下主要是计算像素的梯度变化程度。然而,整数阶微分算子检测边缘时,极容易受到梯度变化程度的影响[12]:梯度变化程度较大的边缘用整数阶微分算子检测就可以获得较好的效果;若是梯度变化程度小到已经无法体现其变化规律时,则整数阶微分算子往往就无能为力了。然而通过大量的研究发现,分数阶微分算子对图像具有低频、甚低频变化特性的信息有非线性增强的效果。不同区间的分数阶微分算子具有不同的作用,就如0~1阶分数阶微分算子[13]:由图1观察便知:0~1阶分数阶微分算子在非线性增强信号中具有低频以及甚低频变化特性的信息的同时较为完整地保留了信号中的高频变化特性的信息。
2 二维分数阶微分泰勒级数函数式提出
2.1 二维函数的泰勒公式
文献[14]推导出二元泰勒级数展开式,而本文在此基础上,进一步推出二元函数的泰勒公式,推导过程如下:
令函数f在邻域U(P)内有连续的k+1阶偏导,则
(3)
并且,n=1,2,…,k,k+1。令x=lcosα,y=lsinα,α是l与x轴正方向的夹角;则函数f的泰勒公式可以表示为
(4)
其中,η是在x0与x之间,ξ在y0与y之间。式(4)就是函数z在l方向的二维函数泰勒公式的展开式。
2.2 二维分数阶微分泰勒级数函数式
由文献[15]可知Grünwald-Letnikov分数阶微分可定义
(5)

将Grünwald-Letnikov定义数值离散化可得到
(6)
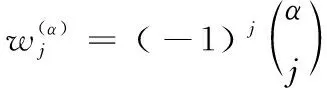
(7)
由式(7)和分数阶微分的定义可构造出分数阶微分公式,所构造公式如下
(8)
其中,η是在x0与x之间,ξ在y0与y之间。
3 二维分数阶方向系数的构建
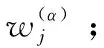
由于数字图像处理领域中的图像是由一系列离散的像素点所组成,那么在本文中分别令Δx=1,Δy=1。以第一象限为例,则4个偏微分分别表示为
则由式(8)可以推得
(9)
通过对式(9)的计算可以分别算得0°、90°、180°、270°方向系数,如下
(10)
(11)
(12)
(13)
4 新Sobel算子的提出
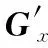
根据上面所算各方向系数定义新的Sobel算子模板梯度如下

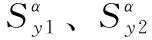
由此得到灰度图像U(x,y)在位置(x,y)处的分数阶梯度为
其中,×表示乘积,*表示卷积。
分别将Sobel算子水平方向和垂直方向梯度算子和方向系数W做乘积运算,形成一个全新的分数阶Sobel算子模板。这种Sobel算子即具有分数阶微分全局性的几何特征又具有整数阶Sobel算子计算简单且分割速度快的特点,使图像强化了感兴趣区域的边缘特征,能够更多地提取图像的细节信息。
5 算法流程
对于灰度图像U(x,y),利用构造的0~1阶二维分数阶泰勒级数权向量滤波的Sobel算子对图像进行边缘检测的算法流程如下:
步骤1 构建二维分数阶微分泰勒级数函数式;
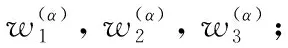
步骤3 推出二维分数阶方向系数W1、W2、W3、W4;
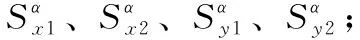
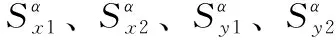
步骤6 计算分数阶梯度幅值
(14)
而
(15)
步骤7 选取分割阈值T:阈值T的选取基于梯度设定边缘点检测的阈值。设灰度图像U(x,y)的图像大小为M×N,则二值化的边缘图像u(x,y)为
(16)
阈值T为
(17)
这里,ξ≥1是一个敏感因子,则当DαU>T时,像素点被标记为边缘点。
由算法流程可知,在利用本算法进行边缘检测时,分数阶微分阶次α和敏感因子ξ的取值决定了边缘检测的效果。因此,要根据具体的待检测图像合理选取分数阶微分阶次α和敏感因子ξ。实验中可以先对分数阶微分阶次α和敏感因子ξ赋予一个适当的值,观察所得结果是否满意,若不满意则可将分数阶微分阶次α和敏感因子ξ作适当修改,直到边缘检测效果最佳时为止。
6 实验结果
为了验证权矩阵滤波的Sobel边缘检测算子性能,分别设计了3个实验:实验一确定敏感因子ξ与分数阶微分阶次α的最佳值;实验二是检验通过边缘检测后的图片的抗噪能力;实验三通过本文算法(参数处于最佳值状态)对目标图像进行处理,与Sobel、文献[8,10,13]边缘检测算子进行对比。
本文实验的操作平台系统为Windows 7.0,程序编写使用Matlab R2012a。
6.1 算法最佳参数的选取
实验一主要通过本文所提出的边缘检测算子对目标图像(cameraman图)进行处理,并分为两个小实验逐次进行,第一个实验任意选取参数ξ,选取分数阶微分不同的阶次α对图像进行边缘检测,根据图像边缘信息的结果确定最佳的分数阶微分阶次α;另一组实验利用确定的最佳分数阶微分阶次α,选取不同的敏感因子ξ对图像进行边缘检测,根据图像边缘信息的结果确定最佳的敏感因子ξ。
第一组实验选定敏感因子ξ=2,通过选用不同的分数阶微分阶次α(0<α<1)对cameraman图进行边缘检测,实验结果如图2所示。
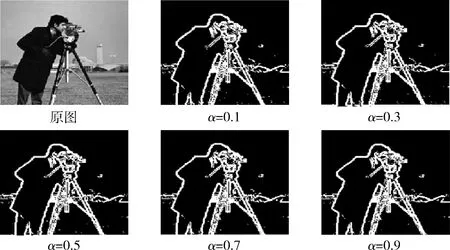
图2 取定敏感因子ξ=1时本文算法(分数阶阶数为不同数值)的实验结果
目标图像纹理信息丰富,由实验结果(即图2)便知:当选用的分数阶微分阶次在α∈(0,1)之间时,所获得感兴趣区域的全局轮廓基本上能以完整的几何边界展现出来;同时本文算法不仅能保留边缘的丰富的纹理信息,还能较为清晰的展现。由此在分数阶微分阶次α∈(0,1)之间任取一值α=0.9作为分数阶微分阶次的最佳值。
第二组实验选定分数阶微分阶次α=0.9,通过选用不同的敏感因子ξ(ξ≥1)对cameraman图进行边缘检测,实验结果如图3所示。

图3 微分阶次α=0.9时不同预设参数的边缘检测结果
从图3的实验结果可以看出:当1≤ξ≤1.8时,随着参数ξ值的依次增大,边缘纹理细节信息越来越丰富,且噪声对实验结果的影响程度逐渐减弱;当ξ≥1.8时,实验效果随着敏感因子ξ的增加而逐渐变差,虽然说滤波效果得到了更好的体现,但是感兴趣区域信息也随之出现缺失。由此便知:ξ=1.8能使目标图像的实验效果达到最好状态,可定为最佳参数。
由实验一可知:本文算法不仅能检测出更丰富的图像边缘纹理细节信息,还能在极大程度上削弱噪声的影响。此外还发现,不同数值的参数ξ所获取的实验结果差异程度非常大;因此,构造本文算法的模板时需选取合适数值的参数ξ。
6.2 本文算法抗干扰能力的检测
为了充分说明本文所构建模板能极大地削弱噪声的影响,将本文算法(参数处于最佳状态,即α=0.9,ξ=1.8)对噪声污染程度不同的目标图像进行处理,并对实验结果差异性进行着重分析。实验中目标图像噪声污染程度的不同是通过对高斯白噪声标准差σ的赋值所体现的。实验对象是flower图。不同噪声水平的图像边缘检测实验结果如图4所示。

图4 含噪声目标图像的实验结果对比
由前文分析便知,本文算子对高频信号具有一定的压缩功能;高频信息一般在图像中以噪声的形式展示。因此,本文算子能削弱噪声对实验结果的影响。同时对实验结果的分析研究可知:随着σ的增大,噪声对原图像的影响越来越大,但本文算子所得的边缘依然清晰可见。
为了充分说明本文算子的抗噪能力优于传统微分算子,本文选用Sobel算子、Canny算子、传统分数阶微分算子、本文算子对flower图(噪声σ=0.05)进行边缘检测,并计算检测结果的psnr值,从表1中可以明确地发现,本文算子较其它算子在提取噪声图像边缘的同时能保持比较高的psnr值。故本文算子由于二维分数阶微分算子对整数阶Sobel算子的滤波,在一定程度上消除噪声对图像边缘的影响。

表1 噪声图像边缘检测的psnr值
6.3 与现有的边缘检测算子的比较
为了充分说明本文算法优异的性能,即目标图像经本文模板处理能获得丰富的纹理细节。目标图像为house图,分别将Sobel、文献[8,10,13]边缘检测算子和本文算子进行实验,使用最佳阈值处理。本文算子实验参数选用实验1的最佳参数,结果如图5所示。

图5 本文算子与常用算子的对比
由图5的分析可知,Sobel算子所检测的边缘不清晰明亮,且出现了一定的断点、信息泄露等情况。分数阶微分算子能够非线性的保留中、低频变化特性的边缘细节,这就导致图中出现大量的噪声;然而当目标物与背景之间的像素梯度变化非常微小的时候,传统的分数阶微分算子也会无能为力,为此才会导致边缘出现些微的断点等现象;就如文献[8,10,13]所获得最佳实验结果。并且分数阶模板对图像中低频信息具有一定加强作用,会保留丰富的纹理细节;就如献[8,10,13]的微分算子所检测的边缘出现了许多噪声点。而本文算子能充分的检测图像中低频变化特性细节,还由于与Sobel算子的结合还能平滑噪声。
为了充分说明本文算子复杂度较其它算子低,本文利用flower图和house图进行实验,将本文算子与检测精度较好的Sobel算子、文献[8,10,13]的算子进行比较。同时,各算子均采用最优参数,然后分别计算各算法在最优参数下对两个目标图像进行实验所需的时间。并将100次不间断实验所得的总时间除以100获得的数据便是上文的所需时间。见表2。

表2 边缘提取的耗时对比
7 结束语
根据分数阶微分Grunwald-Letnikov定义理论,本文所提出改进后的Sobel算子能在一定程度上加强图像中的低频信息的同时还能较为完整的保存图像的中频信息。并通过本文所做的实验分析可知:①本文算法能在极大程度上削弱噪声对图像的影响;②本文算法所获得的边缘纹理丰富;③本文算法运行时间大大缩短。
参考文献:
[1]WANG Chengxiao,HUANG Huixian,YANG Hui,et al.New improved 1-2 order fractional differential edge detection model based on Riemann-Liouville integral[J].Journal of Computer Applications,2016,36(1):227-232(in Chinese).[王程啸,黄辉先,杨辉,等.基于Riemann-Liouville改进的1~2阶分数阶边缘提取新模型[J].计算机应用,2016,36(1):227-232.]
[2]CAO Jiazi,SONG Aiguo.Research on the texture image segmentation method based on Markov random field[J].Chinese Tournal of Scientific Instrument,2015,36(4):776-786(in Chinese).[曹家梓,宋爱国.基于马尔科夫随机场的纹理图像分害方法研究[J].仪器仪表学报,2015,36(4):776-786.]
[3]Huang Guo,Xu Li,Chen Qingli,et al.Research on image denoising based on space fractional partial differential equations[J].Journal of Sichuan University (Engineering Science Edition),2012,44(2):91-98.
[4]Kumar,Sanjay.Fractional fouruer transform and fractional-order calculus-based image edge detection[J].Circuits,Systems,and Signal Processing,2017,36(4):1493-1513.
[5]Mekideche Mohammed,Ferdi Youcef.A new edge detector based on fractional integration[C]//International Conference on Multimedia Computing and Systems-Proceedings,2014:223-228.
[6]NIU Weihua,LI Baoshu,LIANG Guishu.Riemann-Liouville fractional differential enhancement method of digital image[J].Journal of Computer-Aided Design & Computer Graphics,2014,26(12):2189-2195(in Chinese).[牛为华,李宝树,梁贵书.数字图像的Riemann-Liouville分数阶微分增强方法[J].计算机辅助设计与图形学学报,2014,26(12):2189-2195.]
[7]GOU Rong.Image edge detection based on G-L fractional differential[J].Computer and Modernization,2013,3(11):17-19(in Chinese).[勾荣.基于G-L分数阶微分的图像边缘检测[J].计算机与现代化,2013,3(11):17-19.]
[8]HE Chun,YE Yongqiang,JIANG Bin,et al.A novel edge detection method based on fractional-order calculus mask[J].Acta Antomatica Sinica,2012,38(5):776-787(in Chinese).[何春,叶永强,姜斌,等.一种基于分数阶次微积分模板的新型边缘检测方法[J].自动化学报,2012,38(5):776-787.]
[9]TIAN Dan.Research on image denoising and segmentation algorithm based on fractional order variations[D].Shenyang:Northeastern University,2015(in Chinese).[田丹.基于分数阶变分的图像去噪和分割算法研究[D].沈阳:东北大学,2015.]
[10]JIANG Wei,CHEN Hui.New edge detection model based on fractional differential and Sobel operator[J].Computer Engineering and Applications,2012,48(4):182-185(in Chinese).[蒋伟,陈辉.基于分数阶微分和Sobel算子的边缘检测新模型[J].计算机工程与应用,2012,48(4):182-185.]
[11]Zeng Wenjuan,Gao Haibo.Image processing research based on fractional Fourier transform[J].Journal of Software Engineering,2015,2(9):318-327.
[12]Pu Yi-Fei,Siarry Patrick,Zhou ji-Liu,et al.A fractional partial differential equation based multiscale denoising model for texture image[J].Mathematical Methods in the Applied Sciences,2014,37(12):1784-1806.
[13]CHEN Qing,LIU Jinping.Detection and extraction of image edge curves and detailed features using fractional differentiation[J].Acta Electronics Sinica,2013,41(10):1873-1879(in Chinese).[陈青,刘金平.基于分数阶微分的图像边缘细节检测与提取[J].电子学报,2013,41(10):1873-1879.]
[14]NIU Weihua,MENG Jianliang,CUI Kebin,et al.Image enhancement method using grumwald-letnikov fractional directional differential[J].Journal of Computer-Aided Design & Computer Graphics,2016,28(1):129-137(in Chinese).[牛为华,孟建良,崔克彬,等.利用Grümwald-Letnikov分数阶方向导数的图像增强方法[J].计算机辅助设计与图形学学报,2016,28(1):129-137.]
[15]Andrew W Wharmby.The application of the fractional calculus model for dispersion and absorption in dielectrics II. infrared waves[J].International Journal of Engineering Science,2016,104(3):62-74.
