跨座式单轨交通车桥系统随机振动轨道不平顺相关性分析

姜博

1 概述

根据前人研究成果[1～2]建立了跨座式单轨交通车桥系统车辆、轨道梁和轮轨接触模型，基于弹性系统动力学总势能不变值原理推导出车桥系统总势能，建立了整个系统的运动方程，形成了车桥耦合大系统的理论研究基础。采用时域法进行求解方程，研究跨座式单轨交通车桥系统的随机性。轨道不平顺是一个随机的过程，在动力仿真分析中常将其处理为平稳的各态历经的随机过程，它是系统随机振动的激振源。因此，研究和测定轨道不平顺的统计特性，是研究车辆-轨道系统随机振动的基础。

2 计算参数及单元划分

2.1 计算参数

由于本文以重庆市跨座式单轨I期工程（较新线）试验区段Z206-25为工程研究背景分析跨座式单轨交通车桥系统耦合振动，故本文实测数据均来自于该段试验[3]。车辆编组荷载模式见图1所示。

图1 试验车辆编组荷载模式

车辆参数采用文献[4]中日本大阪跨座式单轨列车的参数，轮胎的回正刚度和侧偏刚度取自文献[5]。列车载客量按照超员9人/m2，每车230人选取，乘客体重按50kg算。跨座式单轨交通的轨道梁采用典型试验段Z206-25的等截面PC梁，轨道梁立面和标准截面见图2～3。

图2 Z206-25标准轨道梁（单位：mm）

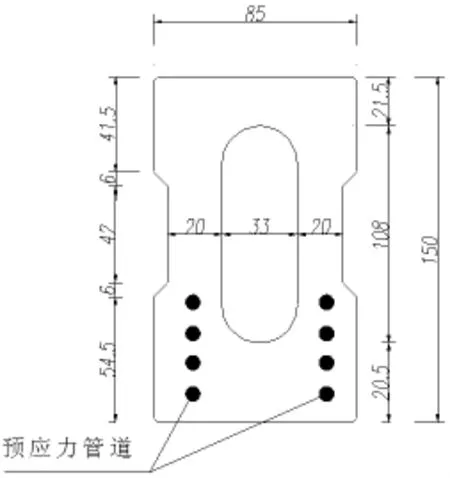
图3 轨道梁截面（单位：mm）

2.2 计算初始条件及单元划分

数值计算采用4节列车编组，如图4所示。计算车速为10～80km/h，车辆初始位移、速度、加速度都为零。计算中取6跨简支轨道梁，其中包括第1、6跨为70m虚拟轨道梁，虚拟轨道梁为以一刚度无限大的梁体，主要给车辆上桥提供一个稳定的初始状态，节省了计算的自由度，每跨刚性轨道梁仅划分为3个梁单元；第2～5跨为22m标准轨道梁。简支梁两端各留0.4m悬臂端并设置支座，不考虑下部桥墩的影响。列车初始位置如图5所示，四辆编组列车位于刚性轨道梁上，车头位于刚性梁与标准轨道梁接缝处，计算开始车辆由刚性梁平稳进入22m标准轨道梁。

图4 车辆编组

图5 列车初始位置

3 轨道不平顺的相关性分析

3.1 轨道不平顺的定义

轨道经过长时间的运营，由于累积变形的不断增大，形成了多种不平顺：高低不平顺，水平不平顺，轨距不平顺。目前，轨道不平顺随机特性的统计包括幅值统计和功率谱统计。一般用功率谱图来描述其变化规律。跨座式单轨交通的走行轮、稳定轮和导向轮均与PC轨道梁直接接触，所以轨道梁的上表面和侧面轨道不平顺是跨座式单轨交通车辆与轨道梁空间耦合振动的重要激振源。目前的相关研究表明，日本对一跨42.8m钢-混凝土组合轨道梁和一跨34.8m钢轨道梁表面不平顺进行了实测并拟合出功率谱密度函数：

式中，Ω为空间频率，单位为cycle/m，α，β，n为功率谱密度函数的相关参数，取值如表1所示。

表1 轨道梁不平顺功率谱密度函数参数值

3.2 轨道不平顺的数学描述

目前轨道不平顺数值模拟方法国内外最常用的的主要有二次滤波法、三角级数法、白噪声滤波法和周期图法。本文采用三角级数法对上述轨道梁表面不平顺功率谱密度函数进行数值模拟，得到不平顺的时域样本可表示为：

式中，ω（x）为所产生轨道不平顺序列；S（ωk）为给定的轨道不平顺功率谱密度函数；ωk（k=1，2，LN）为所考虑的频率，其中ω1、ωn分别为所考虑频率的下限和上限；Dω为频率间隔的带宽；φk为相应的第k个频率的相位，可按照0～2π间均匀分布取随机数值。

轨道不平顺谱的频率范围对车桥系统动力响应的分析结果有很大的影响。尤其长波成分则对车体的振动加速度有较大影响，从而影响旅客的乘坐舒适度。在进行车桥系统振动分析时，轨道不平顺谱波长的范围选择应考虑车辆、桥梁的自振频率和计算车速的范围。从车体振动的最不利情况考虑，计算时所采用的轨道不平顺长波长λ应满足

式中，V是车辆最高行车速度（km/h）；f为车体的自振频率（Hz）。本文跨座式单轨交通车辆V=80km/h，车辆自振频率f=0.912Hz，λ不应小于24.4m，本文波长上限取λ=30m。对于轨道不平顺的短波而言，一般国内外轨检车采取的不平顺采样间隔为0.25m，轨道不平顺对应的最小有效波长为1m。所以波长范围取λ=1～30m。根据日本轨道梁功率谱密度函数，采用三角级数法分别模拟出的一段1000m轨道不平顺样本如图4～6所示。

图4 走行轮轨道不平顺样本

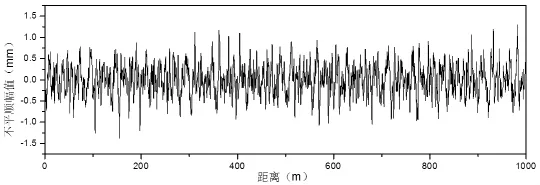
图5 导向轮轨道不平顺样本

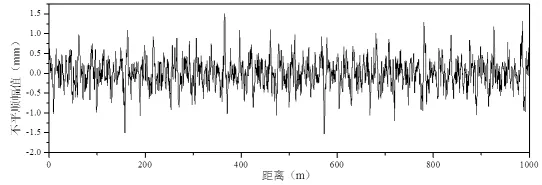
图6 稳定轨道不平顺样本

3.3 轨道不平顺空间相关性

目前，国内外学者在进行铁路桥梁车桥耦合空间振动分析时，常将轨道高低、方向、水平和轨距不平顺中的一种或几种的组合作为输入的激振源。但必须分析各种轨道不平顺类型之间是否相互独立，若存在相关性，则它们同时作为激振源输入时，存在能量重复输入现象，造成车桥振动分析的误差。跨座式单轨交通车桥振动问题存在着竖向走行轮，横向导向轮和稳定轮共6条轨道不平顺的激励样本输入，故分析不同不平顺之间的空间相关性对于计算结果的准确性十分必要。

若轨道不平顺过程用｛η（x）｝表示，距离位移为s，则相关函数Rn（s）为乘积η（x）×η（x+s）的总体平均。研究表明，轨道不平顺可以看做各态历经的平稳随机过程。其相关函数可由下式求得：

均值Ex或Ex+s可由下式求得：

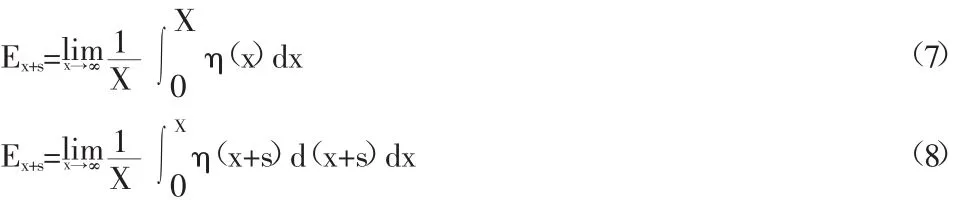
如果试验记录只有在有限区间[0，x]给出，则相应式（5）和式（6）有以下估计式：

列车匀速行驶，则轨道不平顺对可视为时间的平稳随机过程，可知Rη（τ），其表达式为：

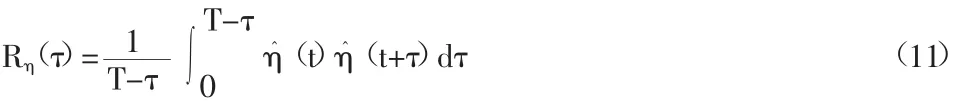
为便于计算，将式（7）和式（8）积分要用有限和来代替。为此，对实测不平顺线作等步长△x抽样，设样本点数为N，则在区间[0，X]内，有：

将式（7）转换为若干区间△x上的求和，则得近似式：

同样的可以对s为0，△x，2△x，…，时计算Rη（s）。例如：

计算积分式（8）的积分区间为：

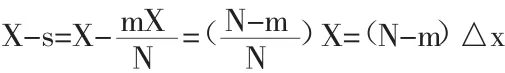
于是：

由式（11）对 m=0，1，2，…计算各种相关函数之值。

为求解Ex和Rn（m△x），采样步长△x应该充分小。按抽样定理，步长应符合：

式中，fc为截止频率。

可见，采样步长将会影响到数据处理的模拟。

如果将式（11）中的（xi）和η^（xi+m）改为1（xi）和2（xi+m），就得到计算两种轨道不平顺互相关函数：

若令式（13）中的m=0，则可得到方差：

最后两种轨道不平顺的互相关系数γη1η2为：

而 γη1η2是一个无量纲的量，且范围为[-1，1]性质[7]：

（1）当 γη1η2=1 时，η1，η2之间为完全线性相关，η1，η2之间存在着确定的函数关系。

（2）当 0≤ γη1η2≤1 时，表示 γη1η2存在着一定的线性相关。 γη1η2的数值愈大，愈接近于1，表示 η1，η2之间直线相关程度愈高；反之 γη1η2的数值愈小，愈接近于0，表示η1，η2之间直线相关程度愈低。若0≤≤0.3 称为微弱相关，0.3≤ γη1η2≤0.5 称为低度相关，0.5≤ γη1η2≤0.8 称为显著相关，0.8≤ γη1η2≤1称为高度相关。

本文运用三角级数法，由日本谱模拟出的6条1km长的跨座式单轨交通轨道不平顺样本之间的互相关系数如表2所示，由表中数据可知它们的范围均在（0，0.3）之间，说明6条样本之间微弱相关，可近似看做彼此独立。所以在跨座式单轨交通车辆—桥梁空间耦合随机振动分析中，6条轨道不平顺样本可以作为激励分别输入。

表2 不平顺之间的相关系数

[1]马继兵.跨座式单轨交通系统静动力行为研究[D].西南交通大学，2008.

[2]曾庆元，杨平.形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J].铁道学报，1986，8（2）：48～58.

[3]重庆市单轨交通系统动载试验研究报告[R].成都：西南交通大学结构工程试验中心，2005，12.

工程试验中心，2005，12.[4]Chang Hun Lee，Chul Woo Kim，et al. Dynamic response analysis ofmonorail bridges under moving trains and riding comfort of trains [J].Engineering Structures，2005，27（14）：1999～2013.

[5]任利惠，周劲松，沈钢，刘绍勇.基于特征根的跨坐式独轨车辆的稳定性分析[J].同济大学学报（自然科学版），2003，04：469～472.