车身薄壁结构的刚度理论研究及应用

钟巧波 朱永萍 肖春燕

上汽通用五菱汽车股份有限公司 广西柳州市 545007

1 引言

薄壁结构是由薄板件通过冲压工艺形成不同形状，并通过连接工艺组成的结构，能以较小的重量和较少的材料承受较大的载荷，因其良好的力学性能和轻量化特性，在车体结构中被广泛应用。薄壁结构与传统工程结构在力学性能上存在较大差异，其截面形状具有不对称性且壁厚相较于截面尺寸占比很小，在载荷作用下除了整体变形外还存在局部变形的情况。本文通过薄壁结构理论研究，识别结构的几何形状和材料特性对刚度和轻量化方面的影响，方便在车身设计过程中，能够使用更少的重量，得到更为优异的结构性能，同时减少反复尝试的时间。

2 薄壁结构的弯曲刚度特性及轻量化理论

2.1 薄壁结构弯曲刚度特性

根据材料力学刚度影响要素，我们很容易推导出结构弯曲刚度公式：

KB=fi×E×I

其中，fi是系数，与结构的边界约束条件、作用位置有关，不同约束条件的fi值见表1；E是材料弹性模量，与材料有关，比如钢铁、塑料、铝合金；I是惯性矩，与截面形状，材料厚度有关。

在常规车身结构设计过程中，结构边界条件相对固定，因此，可以通过选用弹性模量E更高的材料或者优化截面惯性矩I来提高结构弯曲刚度，而对于以钢材为主的车身结构，在车身结构设计过程中，则需要重点提升截面惯性矩来提高结构弯曲刚度。

2.2 惯性矩的计算

截面惯性矩是影响结构承载能力的重要因素，根据惯性矩知识，矩形薄壁结构和圆形薄壁结构的惯性矩如下：

（1）对于矩形薄壁截面（如图1），

由于料厚t相对于矩形高度h和宽度b很小，我们将公式进行近似处理：

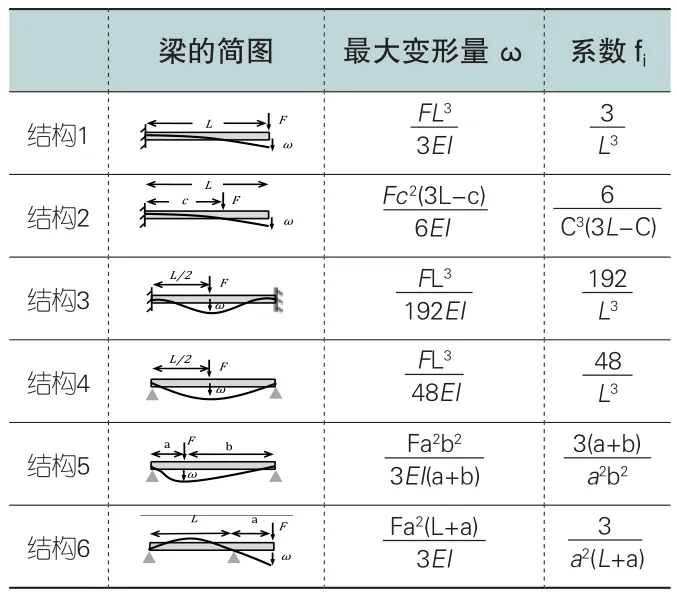
表1 典型结构梁的最大挠度和系数

图1 矩形薄壁截面

其中b，h分别为薄壁梁截面厚度t中线处的宽和高。

（2）对于圆形薄壁截面（如图2），同样做相似处理：

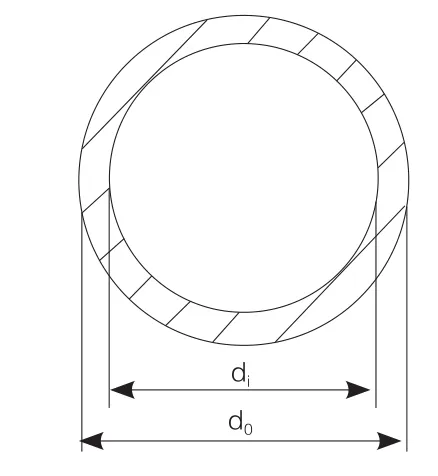
图2 圆形薄壁截面

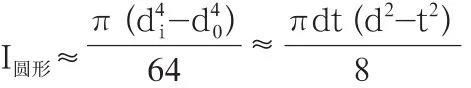
其中，d为为薄壁梁截面厚度t中线处的直径。

由结果可知，对于矩形截面，腔体的高度h对惯性矩影响较大，其次为材料厚度t，腔体的宽度b对惯性矩影响较小；对于圆形截面，腔体直径d对惯性矩影响较大，其次为材料厚度t。

2.3 薄壁结构弯曲刚度的轻量化理论

相同材料条件下，结构的重量和结构截面的材料面积成正比，从轻量化角度考虑，我们需要提高结构截面的效率，为此我们引

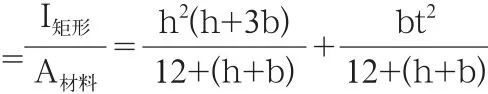
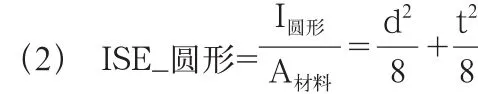
由于d t，所以t^2/8相对于d^2/8言占比非常小，因此增加d可以明显提高截面惯性矩效率，增加t效果不明显。

2.4 薄壁结构弯曲变形的局部刚度特性

薄壁梁结构和理想梁结构在受到集中载荷作用下的弯曲变形过程中，理想梁结构通过弯矩来影响结构变形，而薄壁梁结构除受到弯矩作用外，在载荷作用点附近还会产生局部变形，这种局部变形会导致薄壁梁结构刚度变弱，并且出现局部应力。

薄壁梁在受到集中载荷作用时，其变形量等于对应的理想梁变形量加上其截面的局部变形量，可等效视为两组弹簧的串联关系，如图3所示的矩形薄壁梁结构，其截面局部刚度公式为：

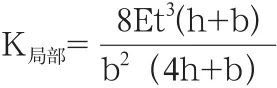
图3 薄壁梁结构局部变形图示

以图3（a）为例，假设L=1500mm，h=b=100mm，t=0.8mm，E=207000N/mm2，I=5.33×105mm4；

系统刚度为：N/mm

由于薄壁梁结构存在局部变形，使得其实际刚度只有理想刚度的2%。因此，需要通过局部结构优化来改善刚度，常用优化方法有增加局部加强件，将载荷引到侧壁，增加贯穿腔体结构，减小载荷面尺寸，增加筋条等。

3 薄壁结构的扭转刚度特性及轻量化理论

3.1 薄壁结构扭转刚度特性

薄壁结构理论的扭转刚度公式与弯曲刚度公式相似，表达如下：

其中，fi是系数， 与结构的边界约束条件、作用位置有关；G是材料的剪切刚度模量，与材料有关，如钢铁、塑料、铝合金；Ip是极惯性矩，与截面形状，材料厚度有关。

与弯曲刚度理论相似，在车身结构设计过程中，则需要重点提升截面极惯性矩来提高结构扭转刚度，薄壁结构截面形状一般分为闭环和开环两种，如图4所示，两种截面形式的极惯性矩不同。对于任意形状闭环截面和开环截面的极惯性矩为：

图4 任意形状开环和闭环截面

其中，A为闭环中线所包围的面积；S为材料中线的长度；t为薄壁结构厚度；

由以上理论公式可知，闭环截面的极惯性矩与材料中线所包围面积的平方成正比，与料厚成正比，与材料中线长度成反比；开环截面的极惯性矩与料厚的立方成正比，与材料中线长度成正比。由于料厚t相对于A和S来说很小，因此在相同条件下，闭环截面的极惯性矩远大于开环截面的极惯性矩，即闭环结构扭转刚度远高于开环结构。

3.2 薄壁结构扭转刚度的轻量化理论

任意形状闭环截面和开环截面中，其材料面积A材料=S×t，因此：

以此对照，看看我们的出版专业硕士，几乎没有门槛，985在办、211在办，二本在办，三本也想办。结果自从有了出版专硕，我们的学术硕士质量明显下降，有的学校甚至招不到学生。

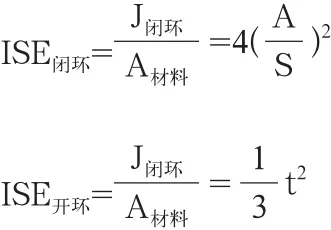
可见，在相同材料面积的下，对于闭环截面，改变A/S，即改变截面形状可以有效提高截面的极惯性矩效率，根据几何原理，A/S比值由大到小分别为圆形，正六边形，正方形，长方形，三角形；对于开环截面，只有通过增加料厚才能提高极惯性矩效率。

4 薄壁结构的屈曲理论及其优化方案

4.1 薄壁结构在压力载荷下的屈曲理论

由前文的薄壁结构的刚度理论我们可知，相同的材料面积，当把材料远离中性轴后，可以提升结构的惯性矩，弯曲刚度随之增加。那么把材料无限远离中性轴后，我们是否可得到非常大的弯曲刚度呢？

结果必然是否定的，实际上，给细长杆或薄壁腔体施加一个载荷，载荷逐渐增加，当载荷很小的时候，细长杆或薄壁腔体的变形与载荷成正比，但当载荷超过某一值的时候，由于在轴线或柱面的垂直方向出现大量横向紧缩，导致结构无法维持原有特性的平衡状态，最后出现崩溃，这一现象称为屈曲，出现屈曲时的载荷称为屈曲载荷，出现屈曲时的应力称为临界屈曲应力，临界屈曲应力取决于板的宽厚比b/t。

在薄壁理论中，薄壁板在受到压力载荷时，局部区域由于发生屈曲现象会降低整个结构的承载能力，如果我们能够提高屈曲区域的临界屈曲应力，就可以有效提高整体结构的承载能力。为了更好的理解，我们将临界屈曲应力公式进行变形：

图5 屈曲应力与宽厚比关系

其中：k为屈曲系数，与约束边界条件和受力情况有关，如图6所示；E为是材料弹性模量；μ为材料的泊松比，与材料有关；b为板的宽度；t为板的厚度。

由变形公式我们可以得到3个要素，其中：

（1）（k）为屈曲系数，可以通过增加翻边，增加筋条等方法进行优化；

（2）为面刚度系数，与材料，腔体填充物有关；

（3）与面的宽厚比有关，可以通过增加局部料厚，增加筋条，减小面宽度进行优化。

4.2 薄壁结构在面法向载荷下的屈曲理论

在车身结构中，车身外覆盖件也是车身的重要组成部分。车身外覆盖件一般为尺寸较大且厚度很薄的平面或曲面，我们称之为薄壁面板。薄壁面板在受到面法向的局部载荷过程中，初始阶段载荷和变形关系是线性的，当载荷超过一定值后，薄壁面板会发生曲率反转现象（油罐现象），油罐现象也属于屈曲现象。例如我们在考量顶盖抗凹性的时候，通过拇指按压顶盖，初始时顶盖变形随按压力增加而增加，当按压力增加到一定程度时，顶盖突然出现局部塌陷的问题，为了改善这一问题，我们需要设法提高薄壁面板的面法向刚度。

薄壁面板的面法向刚度公式为：

其中，B为常数；E是材料的弹性模量；μ是泊松比；t是薄壁的厚度；L1，L2为矩形薄壁面板尺寸；HC为冠高，冠高

5 结语

车身结构设计是一项复杂的系统工程，虽然通过理论分析难以得到精确的刚度结果，但仍希望工程师具备薄壁理论分析能力。在设计前期阶段，充分理解结构设计要素和刚度、强度、轻量化之间的关系，根据结构使用情况，灵活运用薄壁结构理论知识进行定性分析，设计出合理的截面形状、尺寸及结构搭接方式，在设计后期，再通过计算机辅助仿真进行定量计算来验证设计方案，从而避免盲目设计，进而减少重复验证次数，并能够使用更少的开发投入和开发时间，得到更为优异的车身性能。

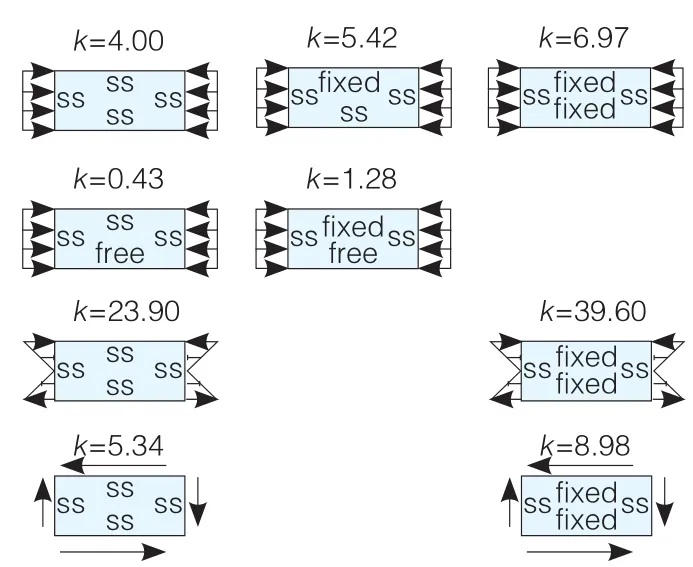
图6 不同约束条件下面的屈曲系数

边界条件 面边缘自由度 边缘约束示意图SS简单支撑 无位移可旋转Flxed固定约束 无位移无旋转Free自有状态 可位移可旋转

图7 薄壁面板在面法向载荷下的变形

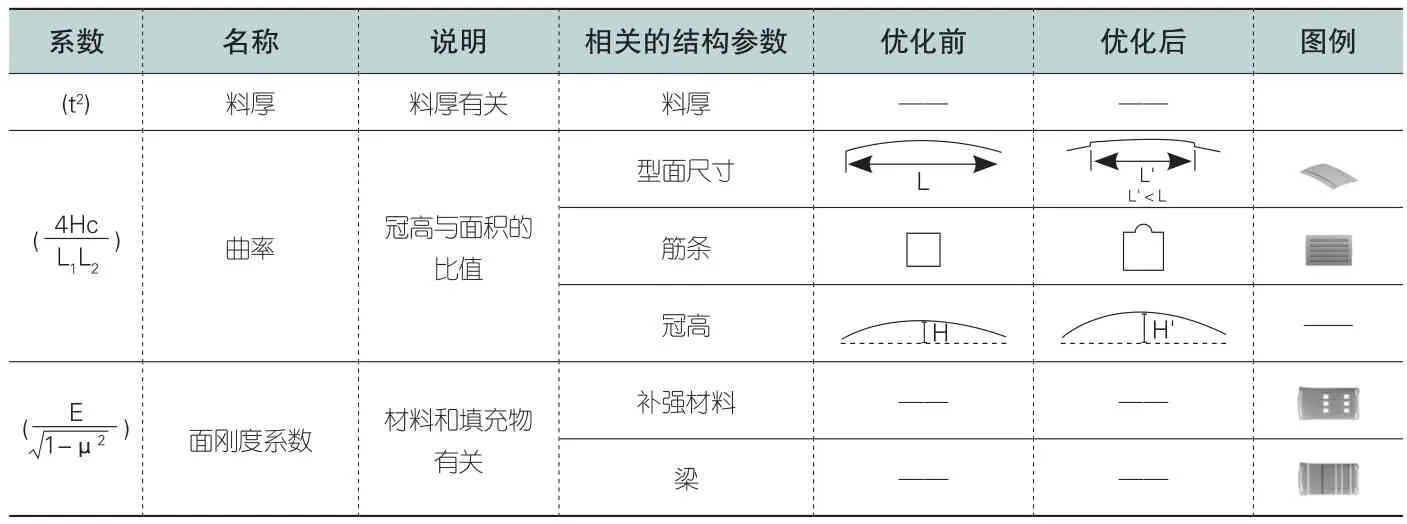
表2 提高面法向刚度的方法