Destroying a Near-Extremal Kerr-Newman-AdS Black Hole with Test Particles∗

2018-06-15YuSong宋宇MingZhang张明DeChengZou邹德成ChengYiSun孙成一and

Communications in Theoretical Physics 2018年6期

关键词：张明

Yu Song(宋宇),1 Ming Zhang(张明),2 De-Cheng Zou(邹德成),3 Cheng-Yi Sun(孙成一),1 and

Rui-Hong Yue(岳瑞宏)3,∥

1Institute of Modern Physics,Northwest University,Xi’an 710069,China

2Faculty of sciece,Xi’an Aeronautical University,Xi’an 710077,China

3Department of Physics,Yangzhou University,Yangzhou 225009,China

1 Introduction

According to the so-called cosmic censorship conjecture,[1]all physical singularities due to gravitational collapse should be hidden behind an event horizon.This hypothesis that no naked singularity occurs in our universe can be described in weak and strong versions.[2]One way of testing the week cosmic censorship conjecture(WCCC)is to throw a test particle into an existing black hole.If the particle can pass through the horizon and change the parameters of the black hole so that the horizon disappears,then the cosmic censorship conjecture might break down.

The seminal work was done by Wald,[3]which showed that a test particle can not destroy the horizon of an extremal Kerr-Newman black hole.From then on,many authors followed the spirit of Wald’s gadanken experiment and revisited the problem of WCC violation.Some of the attempts involving test particles have been successful to produce naked singularities.[4−8]For example,Jacobsonet al.[4]asserted that it would be possible to destroy a Kerr black hole with infalling test particle if we start with a near-extremal con figuration,rather than an extremal black hole.In Ref.[5],Hubeny showed that overcharging a near-extremal Reissner-Nordstrom(RN)black hole is possible by injecting a test particle into the black hole.For charged and spinning black holes,it is possible to destroy an extremal[9]and near-extremal[10]Kerr-Newman black hole by a test particle with electric charge and angular momentum by neglecting the backreaction effect.The issue about the problem of cosmic censorship has been extensively studied in recent years.[11−19]

Since the discovery of the AdS/CFT correspondence,[20−22]its developments have brought about many new insights into the nature of black holes. The study of asymptotically anti-de Sitter black holes has become more important and realistic than ever. It is interesting to know the role of Λ in the discussing turning a black hole into a naked singularity by plugging a test particle into black hole.Recently,Zhanget al.[23]asserted that an extremal Reissner-Nordstr¨om anti-de Sitter black hole can be overcharged by a test particle and both extremal Kerrde-Sitter/anti-de-Sitter black holes can be overspun by a test particle,which implies a possible breakdown of the cosmic censorship conjecture.Moreover,we have also recovered that a test particle may destroy the horizon of an extremal Kerr-Newman-AdS black hole,resulting in an apparent violation of the cosmic censorship.[24]In this paper,we further study the near-extremal Kerr-Newman-AdS black holes,and will find that the possibility to destroy a near-extremal Kerr-Newman-AdS by plunging test particles across their event horizon when neglecting the self-force,self-energy,and radiative effects.We also pro-vide a numerical plot showing that a test particle,which potentially could destroy the black hole,could really fall all the way from in finity into the black hole.

In Sec.2 we show how a near-extremal Kerr-Newman-AdS black hole can be destroyed by plunging test particle across its event horizon.Finally in Sec.3,we give a closing remarks.In this paper we use the unit system wherec=G=~=1.

2 Destroying Near-Extremal Kerr-Newman-AdS Black Hole

In four-dimensional spacetime,the Kerr-Newman-AdS metric takes the following form in Boyer-Lindquist-type coordinates[24−25]

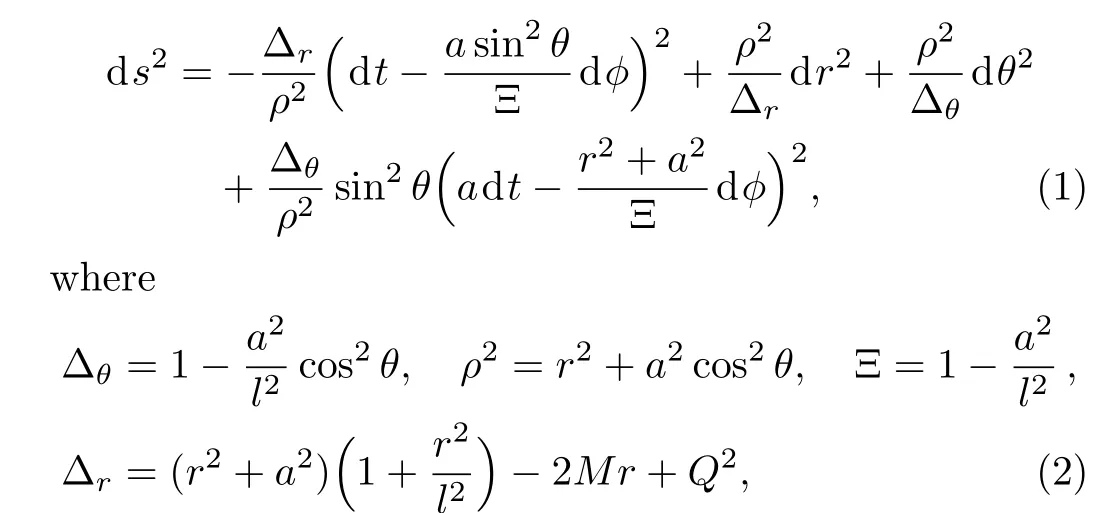
in whichM,a,andQis the mass,angular momentum per unit mass,and charge of black hole,respectively.lis the curvature radius determined by the negative cosmological constant Λ =−3l−2.The radius of the black hole’s outer(event)horizon and inner(Cauchy)horizon are given by[25]

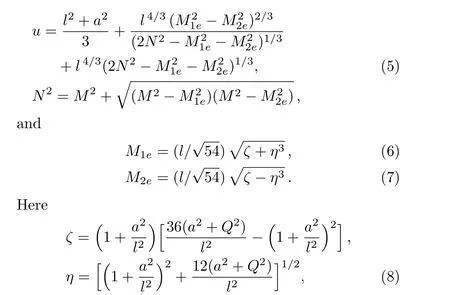
whereM1eandM2eare two extremal mass parameters.It is easy to show that only the mass parameterM1ehas a definite physical meaning.The black hole mass parameterMmust satisfy the relation[25]

with 0≪δ≪M.Then we can obtain

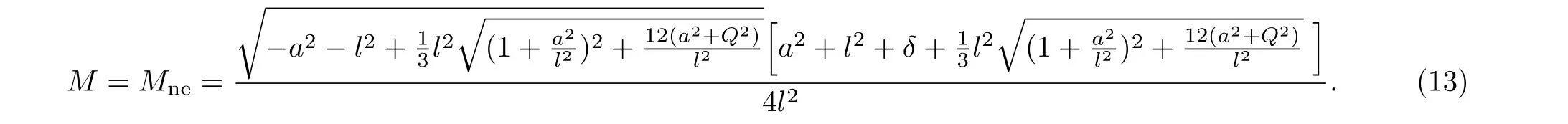
We consider a test particle with electric chargeq,energyE,and orbital angularLcaptured by a near-extremal Kerr-Newman-AdS black hole.After capturing the test particle,the black hole is described by the changed parameters.[26]

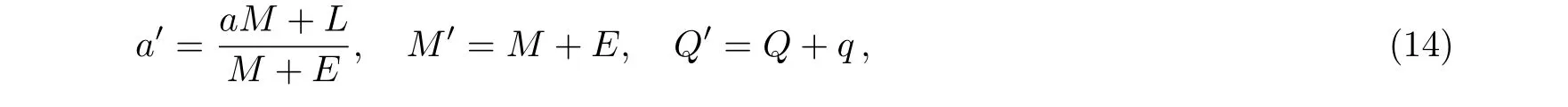
where′is used to describe the changed parameters after capturing a test particle.Then the new extremal condition can be written formally as

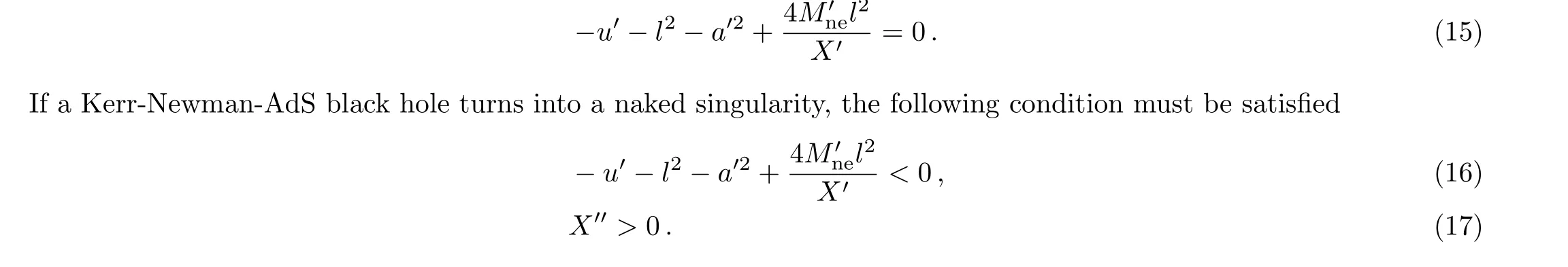
For simplicity,the above condition can be defined formally as

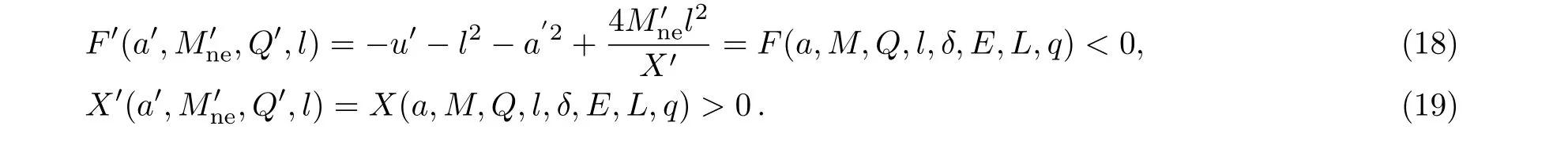
Equation(18)means that the event horizon of black hole is destroyed and a naked singularity appears,it implies that the test particle has a maximum valueEmaxto destroy the black hole.And Eq.(19)ensures that Eq.(18)can be used as a physical criterion for destroying the black hole.

Now let us consider a test particle with electric chargeq,energyE,and orbital angularLmoves along a geodesic in a Kerr-Newman-AdS spacetime,the conserved energy of the test particle is described as[24,27]

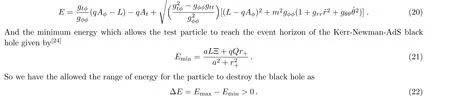
To investigate the range of energy∆E,we chose the parametersQ=23.217 58,a=0.1,q=0.1,L=0.1,then the radius of extremal black hole is 3.638 34 and massMis 100.By choosing the values ofδ,we can get the corresponding values ofEmaxby solving Eq.(18),so one can get a set of values[δ,Emax]for plotting the curve ofδ-Emax,which we provide in Fig.1(b).

In order to get the minimum energy for the particle to reach the event horizon,we can rewrite Eq.(12)as

Fig.1 (a)Plot of E-X′.X ≥ 0 assure the extremal condition of black hole we used as a judgment is meaningful.(b)Plot of E-δ.the shadow area is EEmin.

Based on Eqs.(21),(24),(25),by using the same parametersQ=23.217 58,a=0.1,q=0.1,L=0.1 as mentioned above,we can plot the curve ofδ-Eminwhich we show in Fig.1(b).To prove Eq.(19)is satis fied,using the same numerical values withδchosen to be 0.004,we providefig.1(a).

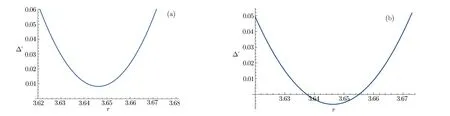
Fig.2 Plot of ∆′-r after capturing a test particle.(a)Plot of ∆′-r.E=0.636 with δ chosen as 0.001.(b)Plot of∆′-r.E=0.638 with δ chosen as 0.001.

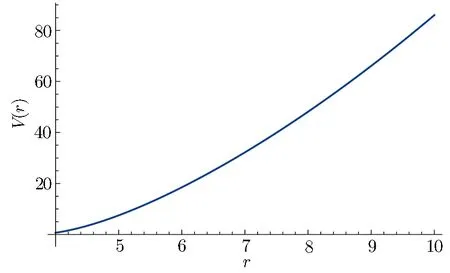
From Eq.(24),we can see the value of functionuwill decrease asδincreases,so ifδtakes values in[0,0.004],δis chosen to be 0.004 will give the minimum value ofX.From Fig.1(a),we can see when particle’s energyEranges from 0 to 3,the condition Eq.(19)is always satis fied.Figure 1(b)shows∆Egets narrower asδincreases,this implies that the black hole is harder to destroy when it moved from the extremality.We can see there is a narrow range of the test particle’s energy,∆E,which allows the appearance of naked singularity from both the near-extremal and extremal Kerr-Newman-AdS black hole.For extremal case(δ=0),we get 0.638 402

From Fig.2(a),we can see the real solution does not exist anymore.This implies that the event horizon is destroyed and the naked singularity is produced after absorbing a test particle.On the other hand,if we choseEis 0.638,which is slightly larger than theEmax,withδchosen to be 0.001,we get the plot of ∆′-rin Fig.2(b),which shows there are two different solution of∆′.This means after capturing a test particle,the extremal black hole will have inner horizon and outer horizon.Thus it turns into a common black hole.This implies when the energy of test particle located in[0.635 641,0.637 13],the black hole will be destroyed.

Next,we will show that a particle from in finity whose energy betweenEmaxandEmincould really fall into the black hole.Since the metric is axisymmetric,the test particle can fall along the orbit which lying entirely in the planeθ=π/2.For such an orbit,one can solve Eq.(20)for˙r2,[9]and obtain

By choosing the same parameters withδchosen to be 0.001,andm=E=0.636 such thatEis in the allowed range,we plot Fig.3.

Figure 3 shows curve is descending and the particle is easy to fall into a Kerr-Newman-AdS black hole from infinity.The choicem=Eindicates that the particle stays at rest relative to a stationary observer at in finity,so it is realizable in practice.

Fig.3 The effective potential V(r)of a test particle outside event horizon with 4

3 Closing Remarks

In this paper,we have found that a test particle may destroy the horizon of a near-extremal Kerr-Newman-AdS black hole,resulting in an apparent violation of the cosmic censorship without taking into account the radiative and self-force effects.Moreover,the allowed range for the particle’s energyEto destroy the black hole is narrow,which indicates that the energy of the particle must be finely tuned.Generally,it regards that taking the radiative and self-force effects[28−30]into account could compensate for the WCC violations.

It is worth to point out that in Refs.[9–10,27],the higher order term in evaluating the allowed upper limit of particle’s energyEmaxis neglected.While in our paper,we sacrifice the analyticity ofEmaxand use the numerical method,so we can plot the allowed range for test particle’s energy to destroy the Kerr-Newman-AdS black hole without approximation.Figure 1(b)we obtained is similar to Fig.4.1 in Ref.[27],both of Fig.1(b)and Fig.4.1 show ∆Eis very narrow and gets narrower asδincreases in the near extremal case.

Nevertheless,the analysis performed in this paper neglects the radiative and self-force effects.The fact that∆Eis very small leaves the possibility of radiative and selfforce effects considerations to cure the problem of WCC violation in Kerr-Newman-AdS spacetime.We will address these projects in our future work.

Acknowledgments

We are extremely grateful to Hao Tang,Bin Wu for useful discussions.

[1]R.Penrose,Revistas del Nuovo Cimento 1(1969)252.

[2]P.S.Joshi,Gravitational Collapse and Spacetime Singularities,Cambridge University Press,Cambridge(2007).

[3]R.M.Wald,Ann.Phys.82(1974)548.

[4]T.Jacobson and T.P.Sotiriou,Phys.Rev.Lett.103(2009)141101,[arXiv:0907.4146[gr-qc]].

[5]V.E.Hubeny,Phys.Rev.D 59(1999)064013.

[6]M.Richartz and A.Saa,Phys.Rev.D 78(2008)081503.

[7]G.E.A.Matsas,M.Richartz,A.Saa,et al.,Phys.Rev.D 79(2009)101502.

[8]M.Richartz and A.Saa,Phys.Rev.D 84(2011)104021.

[9]S.Gao and Y.Zhang,Phys.Rev.D 87(2013)044028.

[10]A.Saa and R.Santarelli,Phys.Rev.D 84(2011)027501[arXiv:1105.3950[gr-qc]].