Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field

E.Ghasemian and M.K.Tavassoly

Atomic and Molecular Group,Faculty of Physics,Yazd University,Yazd,89195-741,Iran

1 Introduction

The interaction between atomic dipole moments and the vacuum state of a quantized field leads to spontaneous emission(SE).Experimental results show that the SE from excited atoms can be either enhanced or suppressed.[1−2]The recent progress of Bose-Einstein condensate(BEC)in magnetic traps has created a new state of matter where all atoms share a single macroscopic quantum state.[3]This leads to great opportunities to explore and test new phenomena related to macroscopic quantum coherence.In recent years authors have theoretically studied SE in a trapped BEC.In this respect,the continuous center-of-mass momentum distribution leads to an increase of SE.[4−5]In this line of research,different physical aspects and various usefulness of BEC systems have been recently considered and discussed.[6−9]It should be noted that,the dynamics of BEC systems and their corresponding interesting topics have been mostly investigated,as a few one may refer to the interference effects between two BECs,[10]super fluidity and coherence in BECs[11]and many of fundamental challenging papers have been published elsewhere.[12]The process of collective SE in the Dicke model has been investigated in the literature.An exact solution for the SE of a multi-photon single-atom Dicke model has been obtained.[13]Also,the SE in the presence ofNatoms was analytically presented for the case in which only one atom is initially excited.[14−15]The collective SE from a system of two atoms with multiphoton transitions in a cavity has been studied in Ref.[16].Collective SE from a BEC in the framework of a multiphotonq-deformed Dicke model has been investigated in Ref.[17]The effect of atomic collisions on the collective spontaneous emission from anf-deformed BEC has been studied.[18]Lately,controlling SE noise in measurementbased feedback cooling of a BEC has been reported.[19]A general theoretical model of the interaction between a single-mode cavity field and the excitons,which leads to collapses and revivals of exciton emission in a semiconductor microcavity has been presented.[20]Recently,we investigated the quantum dynamics of a system consisting of atomic BEC and a single-mode quantized field in the presence of interatom collisions,which leads to clear collapse-revival(CR)phenomenon specially in the atomic population inversion.[21−22]

In the present paper we first give a general theoretical model of the interaction between a single-mode cavity field and a BEC system consisting ofNtwo-level atoms in the presence of interatom collisions and higher-order(nonlinear)interaction of photons,where the atoms are in their excited states.We consider the vacuum state as the initial state of field,therefore,we are able to evaluate the SE in our considered system.Then,to quantify the SE,the expectation values ofˆJzas atomic population inversion(API)in two cases of number and coherent states of atomic subsystem are evaluated.As will be revealed,the collapse-revival(CR)quantum phenomena can be observed.The effects of the number of atoms in BEC,interatom as well as higher-order atom- field couplings and damping parameter on the discussed quantities are studied in detail.At last,we show that,one can find a practical procedure to measure the quantum state of atoms in BEC.

This paper is organized as follows.In the next section,the model and the analytical equations of transformed operators of field and atoms are presented.In Sec.3 we get the analytical expressions for the API(⟨ˆJz⟩)with considering some particular initial conditions for BEC states.We follow our studies in this section with presenting the numerical results.The last section contains a summary and concluding remarks.

2 The Model and Its Solution

According to the experimental results of Meweset al.in 1997,[23]short pulses of rf radiation can be used to create a BEC in a superposition of trapped and untrapped states.In this respect,we consider a system,which consists of a BEC ofNtwo-level atoms in a magnetic trap coupled to an rf field.In fact,the atomic subsystem is a BEC consisting ofNatoms with two internal state(|1⟩,|2⟩)in a magnetic trap,which coupled to a singlemode rf field.The second quantization of the Hamiltonian model is given by

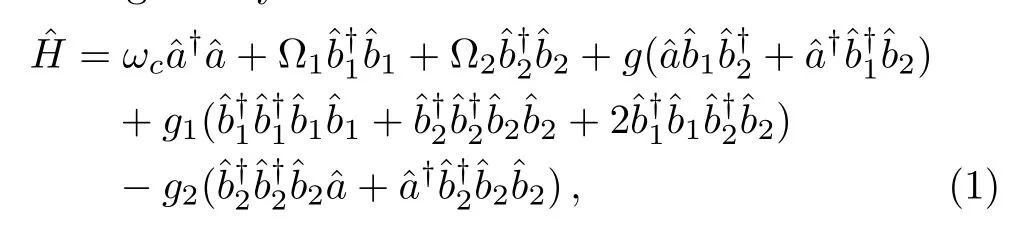
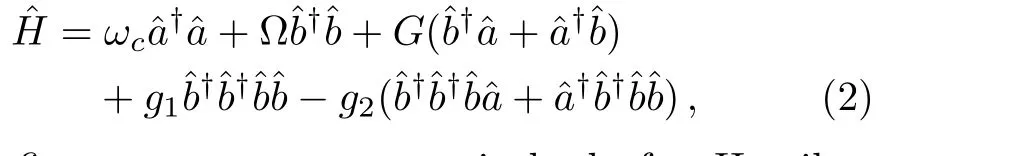
The first-order interaction between the atom and thefield is described by the linear operators of atom and field,[30]therefore,the term contains the nonlinear operators may be referred to as higher-order interaction term.Also,the higher-order atom- field interaction represents the phase-space filling effects as is mentioned in Ref.[31].It should be noticed that,we have neglected a constant term,which contains the average number of the condensate atoms in the state|1⟩(Ω1N1+g1N12),which does not affect the dynamics of the system.Also,it is worthwhile to mention that,the Hamiltonian(2)has been used to investigate the exciton-induced squeezed state of light in semiconductors[29]and the exciton emission of a quantum well embedded in a semiconductor microcavity.[20]To obtain the dynamical evolution of the system,we introduce the following canonical transformations,

By using Eq.(4)the linear part of Hamiltonian(2)can be rewritten as

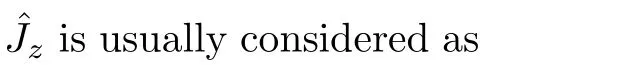
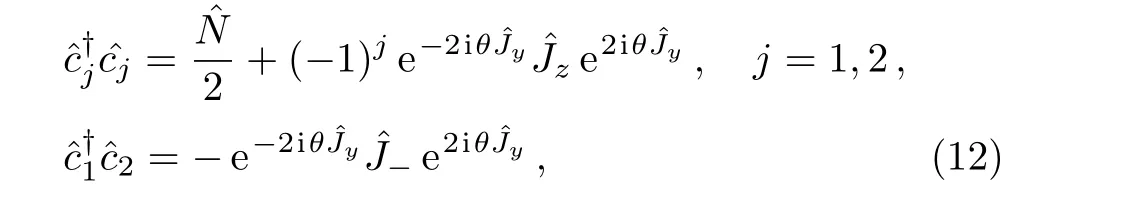
While the first term in above equation is independent of time,the last term is time-dependent and can be rewritten as

This state is indeed a direct product of two number states withj+matoms in BEC andj−mphotons in the cavity field.

3 Spontaneous Emission Rate Using the Atomic Population Inversion(API)

The spontaneous emission(SE)arises from the interaction between atomic dipole moments and the vacuum of the radiation field.To evaluate this quantity,we proceed to investigate the API as a measure for the rate of SE in our considered BEC atomic system.Since,we have represented the BEC operators in terms of the angular momentum operators,therefore,we define API as the expectation value ofˆJz(t)operator as follows:[17]

It is worthwhile to notice that API can also be used to extract information about the rate of energy exchange between the atoms in BEC and the photons of quantized field.Accordingly,in our numerical calculations,we consider the atoms in BEC to be initially in a number(|ψ(0)⟩A=|NA⟩)as well as coherent states(|ψ(0)⟩A=|α⟩)and the field is in the vacuum state(|ψ(0)⟩F=|0⟩).The latter conditions are indeed required for the onset of SE.

3.1 API with Number State as the Initial State of BEC System

where the following definitions have been utilized:[32]

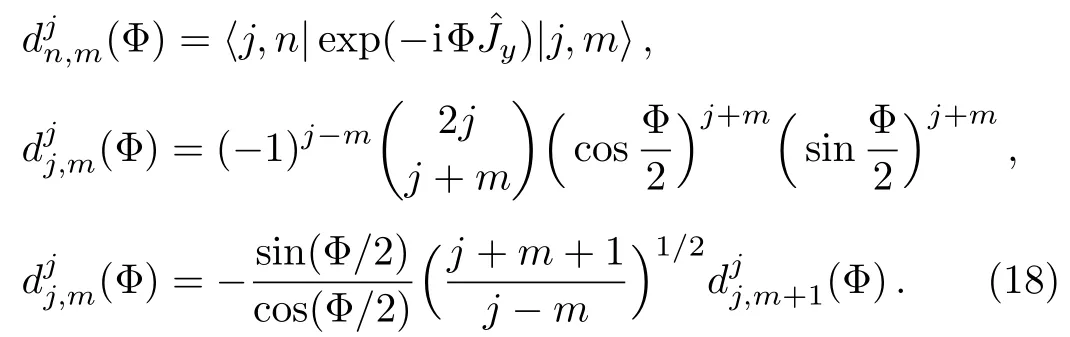
It should be noted that if some realistic conditions are taken into account,it requires High-precision evaluation of Wigner’sdmatrix and some numerical calculations are needed,[33]however,for the chosen resonance case(θ=π/4)one can use the above closed form of the Wigner’sdmatrix to obtain analytical results.Substituting Eq.(17)into Eq.(13)and after some lengthy calculations,we get the API at timetin the number state

In the resonance regime(δ=0),i.e.,θ=π/4,the API reduces to

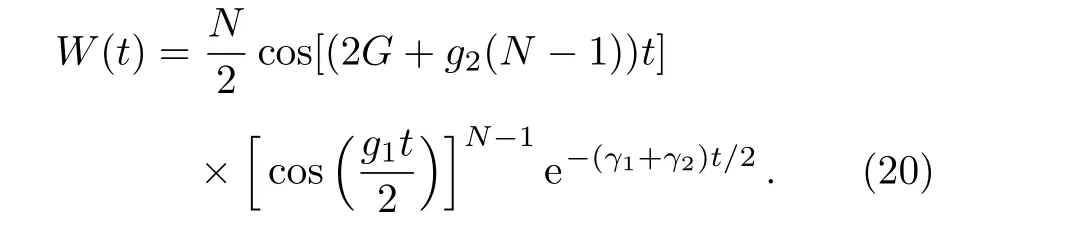
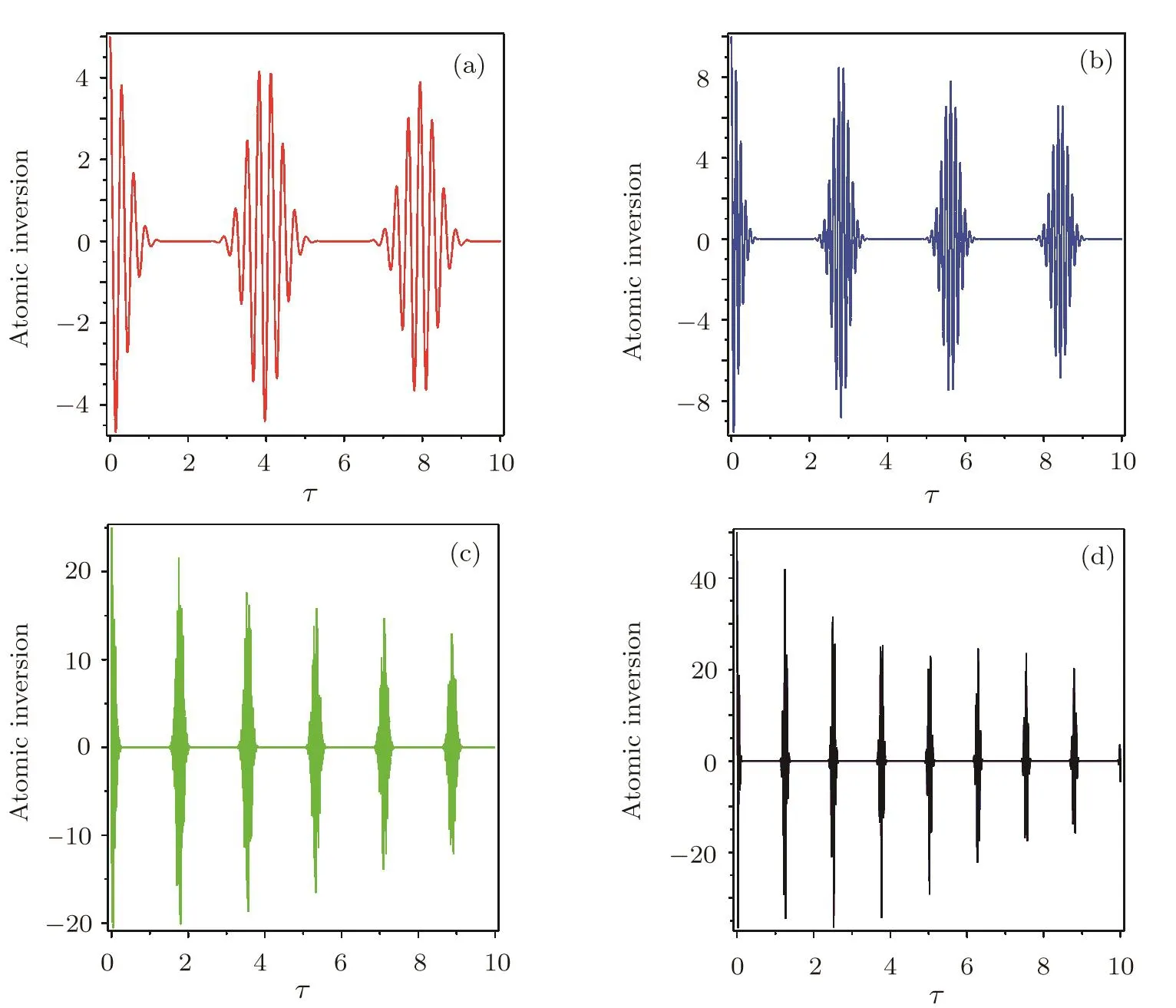
Fig.1 The evolution of API for γ1= γ2=0.01G,g1=g2=0.5G against the dimensionless time τ=gt in the resonance regime.(a)N=10,(b)N=20,(c)N=50,(d)N=100.

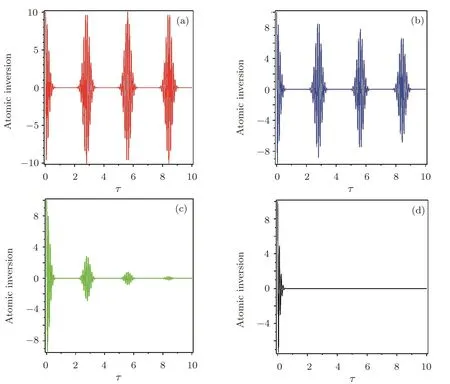
Fig.2 The in fluence of dissipation on the time evolution of API for N=20 and g1=g2=0.5G in the resonance regime.(a)γ1= γ2=0.0,(b)γ1= γ2=0.01G,(c)γ1= γ2=0.1G,(d)γ1= γ2=1.0G.

Fig.3 The effect of interatoms interaction on the time dependence of API for N=20,γ1= γ2=0.01G and g2=0.5G in the resonance regime.(a)g1=0.25G,(b)g1=0.5G,(c)g1=0.75G,(d)g1=G.

3.2 API with Coherent State as the Initial State of BEC System

To achieve more insights into the effect of initial state of BEC atoms on the API,we consider another initial state for the system.In this respect,we assume that att=0 the cavity field is in the ground state and the BEC atoms are in the coherent state.Consequently,the initial state of the total system reads as

where⟨N⟩=|α|2is the average number of atoms in BEC.We can get the final result for the time evolution of API in the coherent state representation by substituting Eq.(21)into Eqs.(13)–(14)leading to

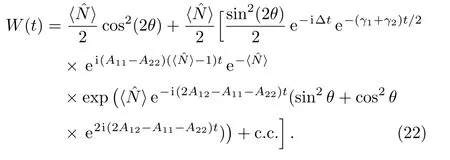
In the resonance regime(δ=0,i.e.,θ=π/4),Eq.(22)is reduced to

Interestingly,the analytical expressions of API in this case are very similar to the results of Ref.[34]in which the authors investigated“macroscopic quantum self-trapping and atomic tunneling in two-species Bose-Einstein condensates”with a different approach.In the coherent state case,the CRs can be occurred even for⟨ˆN⟩<1 due to the quantum superposition properties of the atomic coherent state in BEC.Again,Fig.4 shows that the revival amplitudes of API increases by increasing the number of atoms and the decay process decreases the amplitudes successively in each plot of this figure.In this case,the envelope term e−2⟨ˆN⟩sin2(g1t/4)in Eq.(23)leads to the CRs.

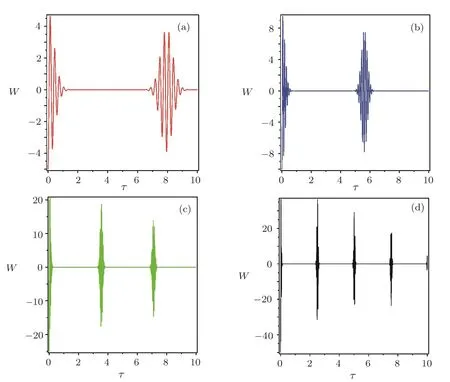
Fig.4 The time dependence of API for different number of BEC atoms with γ1= γ2=0.01G,g1=g2=0.5G in terms of the dimensionless time τ=gt in the resonance regime.(a)N=10,(b)N=20,(c)N=50,(d)N=100.

Fig.5 The effect of interatoms interaction on the time evolution of API for N=20,γ1= γ2=0.01G and g2=0.5G in the resonance regime.(a)g1=0.25G,(b)g1=0.5G,(c)g1=0.75G,(d)g1=G.

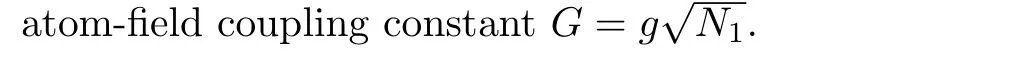
The observation of CRs in nonlinear systems such as the nonlinear directional coupler,[35]the relative phase between two super fluids or superconductors,[36]excitonexciton interaction in a semiconductor microcavity,[32]and the population imbalance of a two-mode BEC[37−40]have been investigated.In this line of research we also showed that the nonlinear interactions in the our presented model can lead to CR phenomenon.

4 Summary and Concluding Remarks

Summing up,we outlined a theoretical model for the investigation of quantum dynamic of BEC interacting with a single-mode quantized field in the presence of interatom collisions and higher order atom- field interaction terms.In this line and to achieve the purpose of paper,at first,via solving the equation of motion the transformed operators of system have been analytically obtained.In the continuation,the API(⟨ˆJz⟩)have been evaluated when two different initial states of the BEC system are considered(number state and coherent state).Our numerical results show that this quantity is very sensitive to the variation of number of atoms in BEC and interatom coupling constant,while the higher-order atom- field interaction does not significantly affect the API.In addition,the collapserevival is an observable quantum phenomenon in the API.In this regard,it may be expected that with the help of our theoretical model and the appearance of collapses-revival phenomenon in the API,the quantum states of atoms in the BEC and photons in the cavity can be measured in practical experiments.

We brie fly present our concluding remarks in what follows:

(i)Number of atoms:by fixing all parameters except the number of atoms in BEC,it is found that increasing the number of BEC atoms leads to the occurrence of more revivals in a definite interval of time,so apparently the intervals of collapse time are considerably decreased.

(ii) Interatomic coupling constant:the occurrence of CR phenomenon in the temporal behaviour of API strongly depends on the interatomic coupling constant.In detail,by tuning the latter parameter,one can control the number of CRs in a fixed interval of time.

(iii)Initial BEC state:it is shown that the time evolutions of both SE or API in the number state and the coherent state as initial states are quite different.In particular,in the number state(coherent state)the revival periods of oscillations read as 2π/g1(4π/g1).The critical requirement of the CRs is the interatom interactions.The behavior of CRs can be controlled by changing the interatom interaction constant(parameterg1).

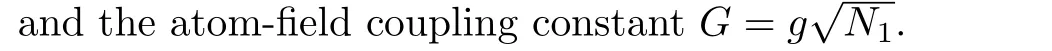
(v)Damping effect:the damping parameter lowers the amplitude of revivals,and change the time of CRs.Indeed,in the weak decay regime there is no considerable change in the CRs time,however,the decaying of amplitude is clearly visible(comparing Figs.2(a),2(b)).By increasing the decay parameters,more the amplitude decay is occurred and the CRs time drastically have been changed(Fig.2(c)).In the enough strong decay regime the API suddenly decreases and tends to zero as time is passed,so that no revival may be created(Fig.2(d)).

Appendix A Derivation of Model Hamiltonian(Eq.(1))

In what follows we bring our detailed calculations,which has been led to Hamiltonian(1).As is well-known,the free atomic Hamiltonian is given by[24]

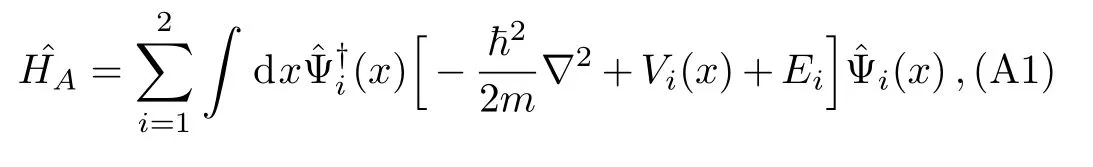
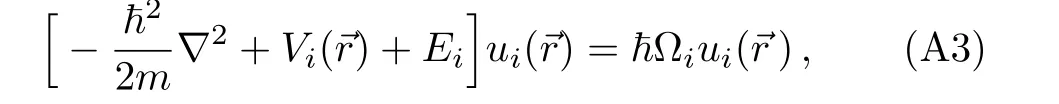
where~Ωiis the energy of modei,and Ωidenotes the frequency of free evolution of the condensate in the internal state|i⟩(more information can be found in Refs.[24–25,28]).Substituting the single-mode expansions of the atomic field operators into Eq.(24),the free atomic Hamiltonian can be rewritten as:

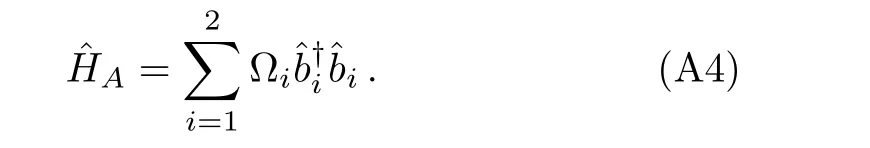
We present the details of our calculations for the first atomic mode as follows:Fori=1,Eq.(24)is reduced to(~=1):

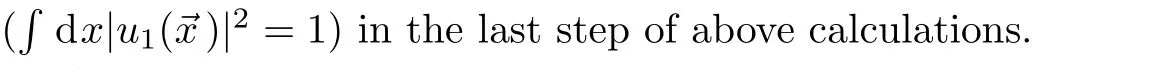
Accordingly,the atom- field interaction in the dipole approximation can be described by the following Ham-iltonian[24]

wheregis the atom- field coupling constant.Also,the interatom(HAA)and higher-order atom- field(HHOA-F)interactions can be written respectively as:[24]

whereg1in Eq.(A9)is the interatomic coupling constant andg2in Eq.(A10)is a constant,which describes the collective response of the many-atom system to the quantized field.

Therefore,the total Hamiltonian of the considered system reads as:

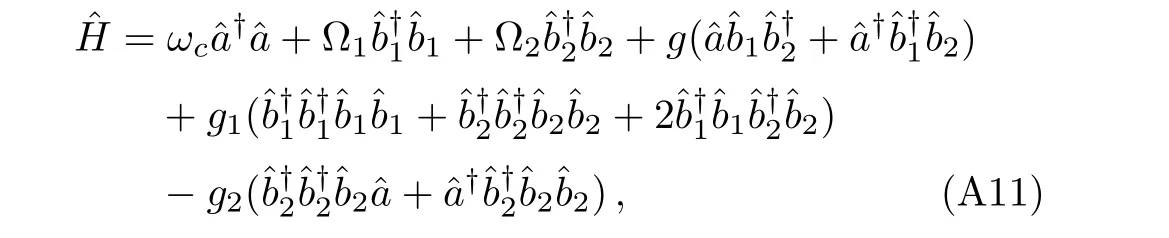
Therefore,in this condition the spatial degrees of freedom is not important due to the integral form of Hamiltonian(see for example Eq.(A1),which is transformed to Eq.(A4).In addition,the Hamiltonians of BEC systems have been presented by using of the Dicke model in which there are no spatial degrees of freedom(see the Hamiltonians of Refs.[17,41]).The same procedure for deriving the second quantized Hamiltonian and more explanations about the spatial modes have been presented in Ref.[25].

Appendix B Derivation of Effective Hamiltonian(Eq.(7))

To obtain the dynamical Hamiltonian of the system,one can insert the relations in Eq.(4)into Eq.(2),so the(effective)Hamiltonian can be reduced to a two-mode Hamiltonian as follows

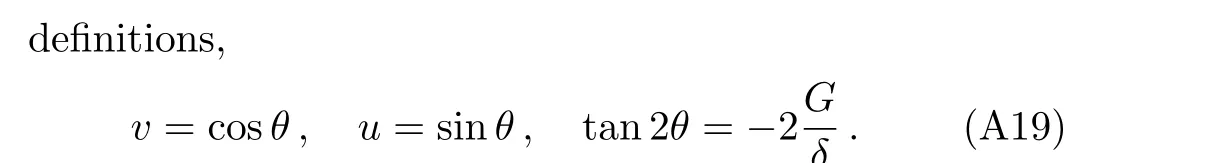
To cancel the last non-diagonal termsH0in Eq.(A17),we use the condition(ωc−Ω)uv=G(u2−v2).Applying all above introduced notations and conditions one obtains:

After omitting the nonconservative-particle-number terms inH1(Eq.(A13))and by a similar manner,which arrived us toH0in Eq.(A20),it can be rewritten and simplified as:

Summing up,one can obtain the effective Hamiltonian of the system as follows

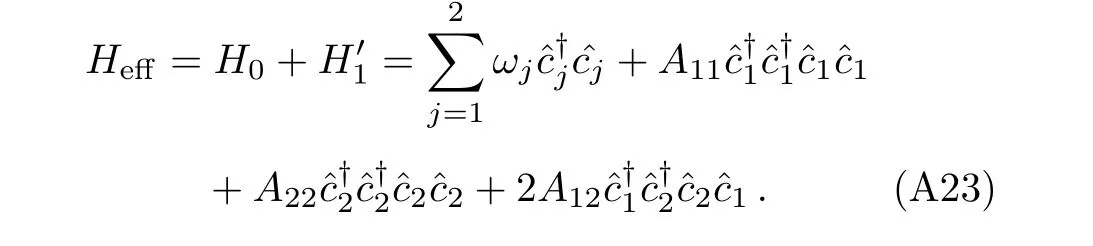
[1]P.Goy,J.M.Raimond,M.Gross,and S.Haroche,Phys.Rev.Lett.50(1983)903.

[2]W.Jhe,A.Anderson,E.A.Hinds,et al.,Phys.Rev.Lett.58(1987)666.

[3]M.Anderson,J.R.Ensher,M.R.Matthews,et al.,Science.269(1995)198.

[4]J.Javanainen,Phys.Rev.Lett.72(1994)2375.

[5]L.You,M.Lewenstein,R.J.Glauber,and J.Cooper,Phys.Rev.A 53(1996)329.

[6]C.Zheng,P.Zhang,and S.Yi,Commun.Theor.Phys.68(2017)236.

[7]Y.X.Huang,N.J.Hui,W.F.Liu,et al.,Commun.Theor.Phys.64(2015)644.

[8]Z.X.Yu and Z.Y.Jiao,Commun.Theor.Phys.36(2001)449.

[9]Z.X.Yu and W.G.Zhang,Commun.Theor.Phys.37(2002)39.

[10]C.M.Savage,J.Ruostekoski,and D.F.Walls,Phys.Rev.A 56(1997)2046.

[11]W.Ketterle,Phys.Scr.T.102(2002)36.

[12]Z.Rapti,G.Theocharis,P.G.Kevrekidis,et al.,Phys.Scr.T107(2004)27.

[13]Z.Chang,Phys.Rev.A 47(1993)5017.

[14]J.Seke,Phys.Rev.A 33(1998)739.

[15]F.W.Cummings and A.Dorri,Phys.Rev.A 28(1983)2282.

[16]A.S.Shumovsky,F.Le Kien,and E.I.Aliskenderov,J.Phys.48(1987)1933.

[17]Z.Haghshenasfard and M.G.Cottam,Eur.Phys.J.D 66(2012)186.

[18]Z.Haghshenasfard,M.H.Naderi,and M.Soltanolkotabi,At.Mol.Opt.Phys.42(2009)065505.

[19]M.R.Hush,S.S.Szigeti,A.R.R.Carvalho,and J.J.Hope,New J.Phys.15(2013)113060.

[20]G.Ri.Jin and W.M.Liu,Phys.Rev.A 70(2004)013803.

[21]E.Ghasemian and M.K.Tavassoly,Phys.Lett.A 380(2016)2362.

[22]E.Ghasemian and M.K.Tavassoly,J.Opt.Soc.Am.B 35(2018)86.

[23]M.O.Mewes,M.R.Andrews,D.M.Kurn,et al.,Phys.Rev.Lett.78(1997)582.

[24]L.M.Kuang and L.Zhou,Phys.Rev.A 68(2003)043606.

[25]M.T.Johnsson,G.R.Dennis,and J.J.Hope,New J.Phys.15(2013)123024.

[26]E.Ghasemian and M.K.Tavassoly,Laser Phys.27(2017)095202.

[27]N.N.Bogoliubov,J.Phys.(USSR)11(1947)23.

[28]C.Huang,J.Fang,H.He,et al.,Physica A 387(2008)3449.

[29]B.A.Nguyen,Phys.Rev.B 48(1993)11732.

[30]M.O.Scully and M.S.Zubairy,Quantum Optics,Cambridge University Press,Cambridge(1997).

[31]M.Kuwata-Gonokami,S.Inouye,H.Suzuura,et al.,Phys.Rev.Lett.79(1997)1341.

[32]G.R.Jin,Z.X.Liang,and W.M.Liu,J.Opt.B:Quant.Semiclass.Opt.6(2004)296.

[33]X.M.Feng,P.Wang,W.Yang,and G.R.Jin,Phys.Rev.E 92(2015)043307.

[34]L.M.Kuang and Z.W.Ouyang,Phys.Rev.A 61(2000)023604.

[35]A.Che fles and S.M.Barnett,J.Mod.Opt.43(1996)709.

[36]F.Sols,Physica B 194(1994)1389.

[37]G.J.Milburn,J.Corney,E.M.Wright,and D.F.Walls,Phys.Rev.A 55(1997)4318.

[38]J.Williams,R.Walser,J.Cooper,et al.,Phys.Rev.A 61(2000)033612.

[39]W.D.Li,X.J.Zhou,Y.Q.Wang,et al.,Phys.Rev.A 64(2001)015602.

[40]P.Zhang,C.K.Chan,X.G.Li,and X.G.Zhao,J.Phys.B 35(2002)4647.

[41]L.Zhou,L.B.Kong,and M.S.Zhan,Chin.Phys.B 17(2008)1601.