Stability Analysis of Solitary Wave Solutions for Coupled and(2+1)-Dimensional Cubic Klein-Gordon Equations and Their Applications
2018-06-15AlySeadawyDianChenLuandMuhammadArshad
Aly R.Seadawy∗ Dian-Chen Lu† and Muhammad Arshad‡
1Mathematics Department,Faculty of Science,Taibah University,Taibah University,Al-Madinah Al-Munawarah,Saudi Arabia
2Mathematics Department,Faculty of Science,Beni-Suef University,Egypt
3Faculty of Science,Jiangsu University,Zhenjiang 212013,China
1 Introduction
Nonlinear partial differential equations exist in all fields of engineering and science,such as optical fibers,lf uid mechanics,plasma physics,chemical kinematics,biology,chemical physics etc. and also utilized to describe the complex aspects in these areas. Thus,the study to search for exact solutions of nonlinear PDEs is extremely crucial.Therefore,to search efficient techniques to construct analytic of non-linear PDEs have pinched a plenty of curiosity via a diverse group of scientists and researchers.Several symbolic techniques have been developed by different researchers and employed to get the exact solutions of nonlinear PDEs in different form,for example;Backlund transformations,[1]variational method,[2]Darboux transformation,[3]modified direct algebraic method,[4−5]auxiliary and simple equation methods,[6−7]Hirotas bilinear method,[8]trial equation technique,[9]inverse scattering scheme,[10]the extended tanh method,the generalized Kudryashov method,[11](G′/G)-expansion method,[12]mapping method,[13]expansion method,[14]and many more.[15−19]In general,there are numerous researchers organized in the area of non-linear science.[20−21]Solitons solutions got more attention of researchers about the study interactions,structures,and more properties.[22−28]
The mean of the current study is to utilize the powerful proposed mapping method for the Klein-Gordon equations.As a result,novel exact solutions in more generalized and different form are obtained.Modulation instability analysis is employed to argue discuss the stability of solitary are solutions in both the normal dispersion and the anomalous regime.
The coupled Klein-Gordon equations:[29]
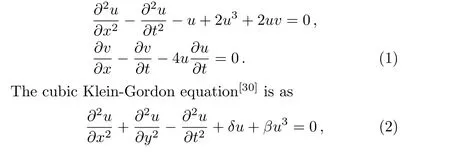
here,the constantsδandβare non-zero.The coupled K-G equation(1)is a relativistic interpretation of the Schr¨odinger equation.It is utilized to express the relation of relativistic energy-momentum in the form of quantized version.The cubic Klein-Gordon equation(2)is utilized to form several different non-linear phenomena,as well as the promulgation of crystals dislocation,the action of elementary particles and the proliferation of fluxions in Josephson junctions.
The rest of paper is ordered as follows.In Sec.1,as an introduction is given.The important steps of proposed modified extended mapping scheme are given in Sec.2.The applications of the proposed method on Eqs.(1)and(2)are revealed in Sec.3.The modulation instability analysis is discussed in Sec.4.The result and discussion are revealed in Sec.5.The conclusion is given in Sec.6.
2 Description of Modified Extended Mapping Method
In this section,we will present the algorithm of modified extended mapping method for nonlinear partial differential equations(PDEs).Let us assume a non-linear PDE in general form having two independent variablexandtas

the functionuis unknown ofxandt,and the functionHis a polynomial with respect touor prescribed variables,which contain both linear and non-linear terms of highest order derivatives of unknown function and can be reduced via employing transformation to a polynomial function in which the all real variable can be amalgamate into a complex variable.The key steps are as:
Step 1Assume that Eq.(3)has the following solution as:
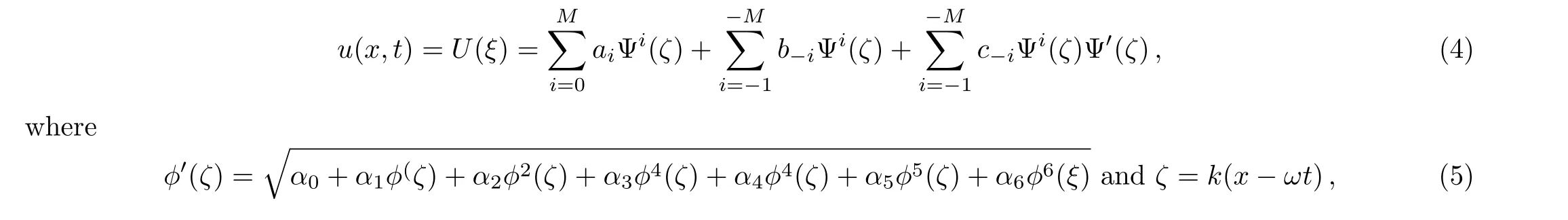
hereai,bi,ci,α0,α1,...,α6,kandωare arbitrary real constants.
Step 2Applying the balancing principle on Eq.(3),and the series of coefficientsa0,a1,...,aM,b1,...,bM,c1...,cM,k,ωare parameters can be achieved.
Step 3Substituting Eq.(4)and Eq.(5)into Eq.(3)and setting the coefficients of different powers ofϕiϕ(j)to zero,yields a system of algebraic equations.These equations are solved by Mathematica software,then the value of parameters can be achieved.
Step 4Putting the parameters value achieved in step 3 andϕ(ζ)into Eq.(4),then the solutions of Eq.(3)can be achieved.
3 Application of Modified Extended Mapping Method
3.1 Coupled Klein-Gordon Equations
Performing the traveling wave transformationu(x,t)=U(ζ),v(x,t)=V(ζ)andζ=k(x−ωt)on Eq.(1),we get

Applying homogeneous balance principle on Eq.(6),we assume the solution of Eq.(6)is as
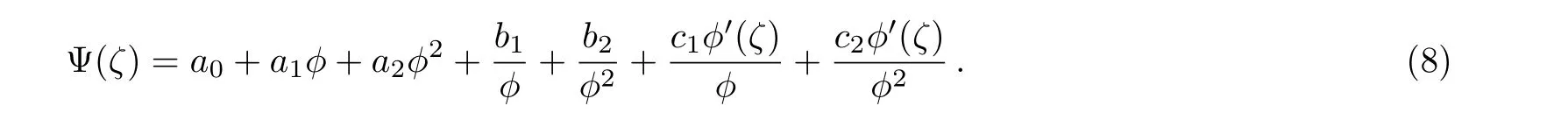
Substituting Eq.(8)into Eq.(6)and setting the coefficients ofϕiϕ(i)to zero,we get a system of equations in parametersa0,a1,b1,c1,a2,b2,c2,α0,α1,...,α6,kandω.Mathematicasoftware is utilized to solve the obtaining system of equations.We obtain the following families of solutions:
Family 1α0=α1=α5=α6=0,
Set 1


The following traveling wave solutions of Eq.(1)are obtained from Eq.(9)as:

One can construct more solitary wave solutions of Eq.(1)from Set 2 in the same way.
Family 2α0=α1=α3=α5=α6=0,
Set 1

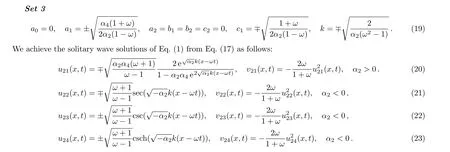
Similarly,we can obtain more solutions in solitary wave form of Eq.(1)from other sets.
Family 3α0=α1=α4=α5=α6=0,

One can achieve more solitary wave form solutions of Eq.(1)from other sets in similar way.
3.2 The(2+1)-Dimensional Cubic Klein-Gordon Equation
Performing the transformationu(x,y,t)=U(ζ)andζ=k1x+k2y−ωton Eq.(2),we get
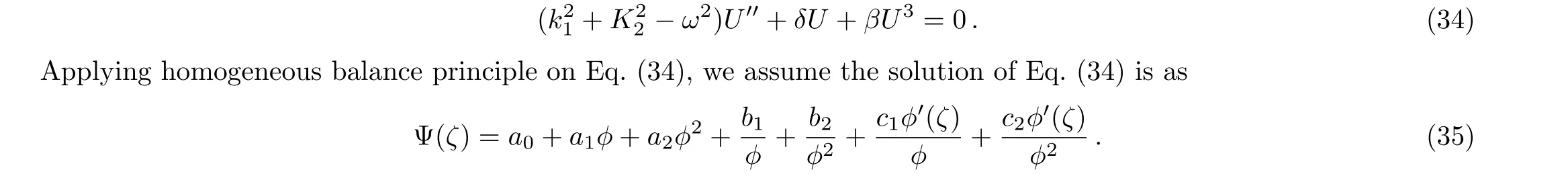
Substituting Eq.(35)along with Eq.(5)into Eq.(34)and setting the coefficients ofϕiϕ(i)to zero,we got a system of equations ina0,a1,b1,c1,a2,b2,c2,α0,α1,...,α6,δ,β,kandω.Mathematicasoftware is utilized to solve the obtaining system of equations.We obtain the following families of solutions:
Family 1α0=α1=α3=α5=α6=0,
Set 1

We obtain the following solitary wave solutions of Eq.(2)from Set 1 as:
We can obtain more exact solutions of Eq.(2)from other Sets in Similar way.
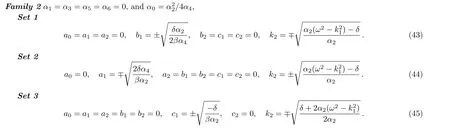
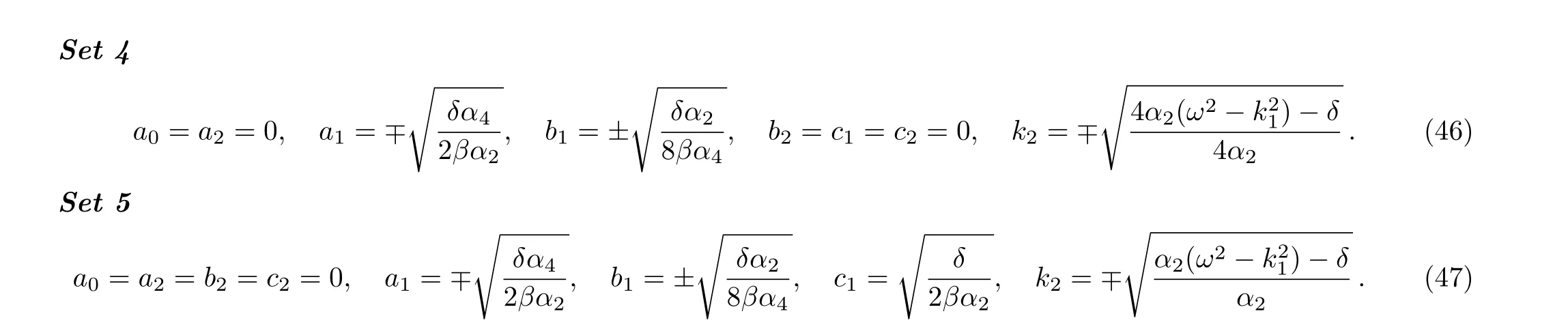
We construct solitary wave solutions of Eq.(2)from Set 1 as follows:

One can obtain more new exact solutions of Eq.(2)from Sets 2–5 in similar way.


In the similar,one can achieve more solitary wave solutions of Eq.(2)from Set 2.
4 Modulation Instability
Several non-linear evolution equations of higher order illustrating an instability that directs to examine the modulation of the steady state as a results of interaction among the dispersive and non-linear effects.The modulation instability of coupled K-G equations and cubic K-G equation are studied by utilizing linear stability analysis(LSA).[31−33]
4.1 Coupled Klein-Gordon Equations
The study state solution of coupled Klein-Gordon equation has the form

where,the wave numberkand frequencyωof perturbation are the normalized.The dispersion relationω=ω(k)of a constant coefficient linear evolution equation enumerates how time oscillations ekxare associated to spatial oscillations eωtofk,putting Eq.(64)in Eq.(63),theω=ω(k)in following form is obtained as

The dispersion relation Eq.(65)reveals the steadystate stability depends on the self-phase modulation,stimulated Raman scattering,group velocity dispersion and wave number.If algebraic expressionH≥0,i.e.theωis real for allk,then the steady state is stable against small perturbations.On the other hand,the steady-state solution becomes unstable ifH<0,i.e.theωis imaginary part since the perturbation grows exponentially.One can easily see that,for the occurrence of modulation stability whenH<0.In this condition,the growth rate of modulation stability gain spectrumh(k)could be revealed as
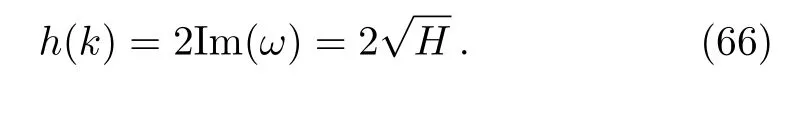
4.2 The(2+1)-Dimensional Cubic Klein-Gordon Equation
The study state solution of(2+1)-dimensional cubic Klein Gordon equation has the form

where,the optical powerPis the normalized.The perturbationψi(x,t)(i=1,2)is investigated via using LSA.Putting Eq.(62)into Eq.(2)and linearizing,yields

Assume the solution of Eq.(68)in the form
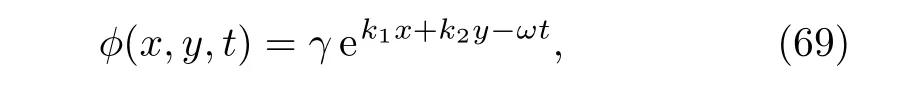
where the wave numbersk1,k2and frequencyωof perturbation are the normalized.Substituting Eq.(69)in Eq.(68),the dispersion relation is obtained in the following form as
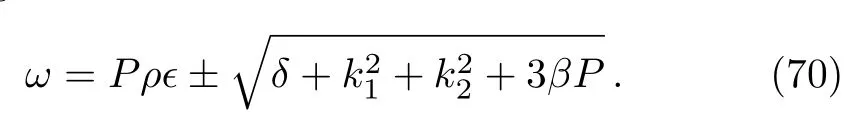
The dispersion relation equation(70)reveals the steady-state stability depends on the self-phase modulation,stimulated Raman scattering,group velocity dispersion and wave number.If algebraic expressionδ+k21+k22+3βP≥0,i.e.theωis real for allk1andk2,then the steady state is stable against small perturbations.On the other hand,the steady-state solution becomes unstable ifδ+k21+k22+3βP<0,i.e.theωis imaginary part since the perturbation grows exponentially.One can easily see that,for the occurrence of modulation stability whenδ+k21+k22+3βP<0.In this condition,the growth rate of modulation stability gain spectrumh(k1,k2)could be revealed as
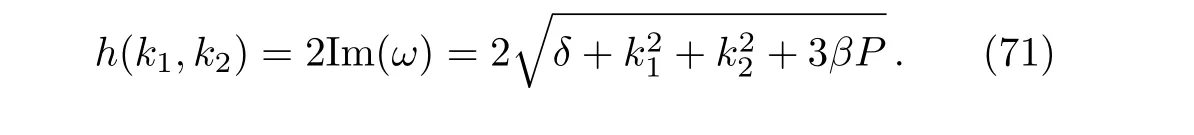
5 Results and Discussion
In this section,we discuss the obtained exact solutions and analyse it with the existing in the literature.
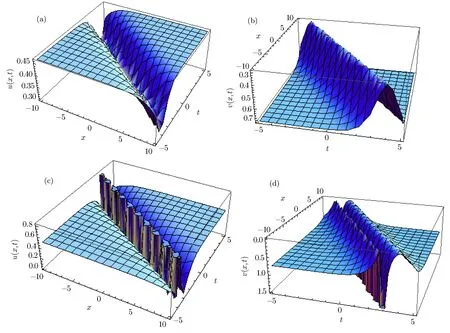
Fig.1 Exact solutions in various shapes are plotted of Family 1 solutions.
Firstly,for the coupled Klein-Gordon equations;the authors in Ref.[29]used the modified simple equation method(MSEM)and achieved some exact solutions in solitary wave form with functions of trigonometric and hyperbolic structure.The obtained solutions(26)and(27)are similar to solutions(3.44)and(3.42)of Ref.[29].The solutions(32)and(33)are similar to solutions(3.43)and(3.41)of Ref.[29].The remaining of our constructed solutions of this equation are novel and have not formulated before.
Secondly,for the cubic Klein-Gordon equation;the authors in Ref.[30]also employed the MSEM to this equation and achieved some exact solutions.The obtained solutions(48)and(60)are similar to solutions(3.18)and(3.19)of Ref.[30].The remaining of our constructed solutions of this equation are novel and have not formulated before.
Analyzing our solutions with the above stated solutions for both models,we determined that our exact solutions are newly constructed solutions with some important physical meaning,for instance;the tangent hyperbolic occurs in the cal-culation of magnetic moment and immediateness of special relativity,the secant hyperbolic occurs in the laminar jet pro file and the sine hyperbolic occurs in the gravitational potential of a cylinder and the calculation of Roche limit.[34]
In Fig.1,Figs.1(a)and 1(b)evaluate dark solitary wave and bright Solitary wave solutions of solution(11)atα2=1.5,α3=1.5,α4=−1,k=0.5,and Figs.1(c)and 1(d)denote the solitary wave solutions in different form of solution(13)atα2=5,α3=1.5,α4=1,k=0.5.Figures 2(a)and 2(b)evaluate Kink Solitary wave and anti-Kink solitary wave solutions of solution(15)respectively atα2=1,α3=2,α4=1,k=0.5,and Figs.2(c)and 2(d)evaluate periodic Solitary wave solutions in different form of solution(20)atα2=1.5,α4=1,ω=1.5.
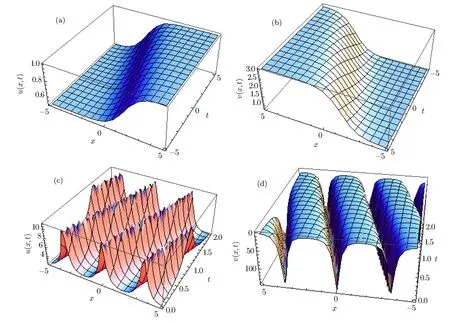
Fig.2 Exact Solitary wave in different shapes are plotted of solutions.

Fig.3 Exact Solitary wave in different shapes are plotted of Family 1 solutions.
In Fig.3,Figs.3(a)and 3(b)evaluate periodic Solitary wave and solitary wave solutions of solutions(39)and(40)respectively atα2=−1.5,α4=1,k1=1.5,k2=1,δ=1.5,β=1.Figures 4(a)and 4(b)evaluate Solitary wave and periodic solitary wave in different form of solutions(48)and(49)atα2=−1.5,α4=1,k1=1.5,ω=1,δ=0.5,β=1 andα2=1.5,α4=1,k1=1.5,ω=1,δ=0.5,β=1 respectively,and Figs.4(c)and 4(d)evaluate dark Solitary wave and bright solitary wave of solutions(52)and(53)respectively atα2=1.5,α3=1.5,α4=−1,k1=1,ω=1.5,δ=0.5,β=1.The dispersion relation(65)among frequency(ω)and wave numbers(k)is shown in Fig.5(a)and the dispersion relation(70)among frequency(ω)and wave numbers(k1,k2)are shown in Fig.5(b).

Fig.4 Exact solitary wave in various shapes are plotted.

Fig.5 Graph of dispersion relation of Eqs.(65)and(70).
6 Conclusion
In this article,we successfully implemented the powerful proposed modified extended mapping method to achieve the solitary wave solutions of the coupled K-G and cubic K-G equations.The obtained solutions are more general and in different forms such as the solitary waves in the form of bright and dark,periodic,hyperbolic etc.We compared our solutions with the existing solutions to these two models and claimed that many solutions are novel.The equations admit the enormous diversity of possible solutions for only values of a small subset of parameters,which helps to understand the physical phenomena’s of this equation.The moments of some solutions graphically and the formation conditions for dark and bright solitons were obtained.An analytic expression for the modulation instability has been established by utilizing modulation instability which con firms that all exact solutions are stable.The efficiency and simplicity of the proposed modified extended mapping method show that it can be used to various types of different nonlinear models that arise in the various areas of nonlinear science.
Competing Interests
This research received no specific grant from any funding agency in the public,commercial,or not-for-pro fit sectors.The authors did not have any competing interests in this research.
Author’s contributions
All parts contained in the research carried out by the authors through hard work and a review of the various references and contributions in the field of mathematics and the physical Applied
Acknowledgment
The authors thank the referees for their suggestions and comments.
[1]Ian M.Anderson and Mark E.Fels,J.Geom.Phys.102(2016)1.
[2]A.R.Seadawy,Eur.Phys.J.Plus130(2015)182.
[3]Qian Zhao,Lihua Wu,and F.Lin,Appl.Math.Lett.67(2017)1.
[4]M.Arshad,Aly Seadawy,Dianchen Lu,and Jun Wang,Results in Physics6(2016)1136.
[5]M.Arshad,A.R.Seadawy,D.Lu,and J.Wang,Chin.J.Phys.55(2017)780.
[6]Kalim Ul-Haq Tariq and A.R.Seadawy,Results in Physics7(2017)1143.
[7]M.Arshad,Aly R.Seadawy,and Dianchen Lu,Optik128(2017)40.
[8]T.T.Jia,Y.Z.Chai,and H.Q.Hao,Superlattice Microst.105(2017)172.
[9]H.Triki and A.M.Wazwaz,Phys.Lett.A380(2016)1260.
[10]M.Lassas,J.L.Mueller,S.Siltanen,and A.Stahel,Physica D241(2012)1322.
[11]H.M.Baskonus and H.Bulut,Entropy17(2015)4255.
[12]M.Song and Y.Ge,Comput.Math.Appl.60(2010)1220.
[13]A.R.Seadawy,Math.Method Appl.Sci.40(2017)1598.
[14]A.M.Syam Kumar,J.P.Prasanth,and Vishnu M.Bannur,Physica A432(2015)71.
[15]J.Zhai and B.Zheng,J.Math.Anal.Appl.445(2017)81.
[16]D.Sinha and P.K.Ghosh,Phys.Lett.A381(2017)124.
[17]Li Min,Tao Xu,and Wang Lei,Nonlinear Dyn.80(2015)1451.
[18]A.R Seadawy,Appl.Math.Inf.Sci.10(2016)209.
[19]A.R.Seadawy and K.El-Rashidy,Math.Comput.Model.57(2013)1371.
[20]Aly Seadawy,Eur.Phys.J.Plus132(2017)1.
[21]A.Atangana and R.T.Alqahtani,Open Physics14(2016)106.
[22]Md.N.Alam and F.B.M.Belgacem,Int.J.Mod.Nonlinear Theory Appl.5(2016)28.
[23]Aly R.Seadawy,Inter.J.Computat.Meth.15(2018)1.
[24]Dianchen Lu,Aly Seadawy,and M.Arshad,Optical and Quantum Electronics50(2018)1.
[25]Aly Seadawy,J.Electromagnet.Waves31(2017)1353.
[26]Aly R.Seadawy,European Physical Journal Plus132(2017)29:1:13.
[27]Aly R.Seadawy,Pramana-J.Phys.89(2017)1.
[28]Aly Seadawy,Optik139(2017)31.
[29]K.Khan,M.A.Akbar,and S.M.R.Islam,Springer Plus3(2014)724.
[30]K.Khan and M.Ali Akbar,J.of the Association of Arab Universities for Basic and Applied Sciences15(2014)74.
[31]G.P.Agrawal,Nonlinear Fiber Optics,5th edition,New York(2013).
[32]M.Arshad,A.R.Seadawy,and D.Lu,Eur.Phys.J.Plus132(2017)1.
[33]Aly R.Seadawy,M.Arshad,and Dianchen Lu,Eur.Phys.J.Plus132(2017)1.
[34]W.H.Beyer,CRC Standard Mathematical Tables,28th edition,Academic Press,Boca Raton(1987).
杂志排行
Communications in Theoretical Physics的其它文章
- Thermodynamic Nonequilibrium Features in Binary Diffusion∗
- Ordinary Mode Instability in a Cairns Distributed Electron Plasma
- Thermal Conductivity of Complex Plasmas Using Novel Evan-Gillan Approach
- Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field
- Molecular Dynamics Simulations of the Elastic Anisotropy of Pd at Extreme Conditions∗
- In fluences of Crystal-Field and Interlayer Coupling Interactions on Dynamic Phase Diagrams of a Mixed-Spin(3/2,2)Bilayer System∗
